延性金屬層裂自由面速度曲線特征多尺度模擬研究*

王云天，曾祥國(guó)，陳華燕，楊 鑫，王 放，祁忠鵬

（1.四川大學(xué)建筑與環(huán)境學(xué)院，深地科學(xué)與工程教育部重點(diǎn)實(shí)驗(yàn)室，四川 成都610065；2.成都理工大學(xué)環(huán)境與土木工程學(xué)院，地質(zhì)災(zāi)害防治與地質(zhì)環(huán)境保護(hù)國(guó)家重點(diǎn)實(shí)驗(yàn)室 四川 成都610059；3.西南大學(xué)材料與能源學(xué)院，重慶400715）

延性金屬在強(qiáng)動(dòng)載荷下的動(dòng)態(tài)破壞是沖擊動(dòng)力學(xué)中重要的基礎(chǔ)科學(xué)問(wèn)題之一，隨著國(guó)防建設(shè)、汽車工業(yè)以及航空航天等領(lǐng)域的發(fā)展，深入地了解延性金屬在高速?zèng)_擊下的動(dòng)態(tài)損傷有著重要的意義[1]。層裂是延性金屬動(dòng)態(tài)損傷的一種典型表現(xiàn)形式，層裂實(shí)驗(yàn)中得到的自由面速度曲線包含了延性金屬在動(dòng)態(tài)破壞過(guò)程中的豐富信息[2-3]。在對(duì)延性金屬層裂行為的研究中，平板撞擊（planar plateimpact,PPI）實(shí)驗(yàn)是目前主要采用的一種研究方法，實(shí)驗(yàn)過(guò)程中內(nèi)部波系傳播如圖1（a）所示：飛片在t0時(shí)刻以一定速度撞擊樣片，二者相撞時(shí)會(huì)分別傳入沖擊波，當(dāng)沖擊波到達(dá)樣片自由面和飛片后表面后會(huì)形成反射稀疏波，兩束稀疏波會(huì)在樣片內(nèi)部相遇并產(chǎn)生拉伸區(qū)域，由此引起的內(nèi)部損傷逐漸累積，直至材料失效斷裂。Curran 等[3]基于對(duì)大量實(shí)驗(yàn)結(jié)果的分析，指出延性金屬的層裂是由于內(nèi)部的微損傷形核、生長(zhǎng)和聚集后，形成層裂飛片的復(fù)雜動(dòng)力學(xué)過(guò)程。

Antoun 等[4]對(duì)層裂的研究歷史和現(xiàn)狀作了權(quán)威性總結(jié)，指出了層裂研究還有許多問(wèn)題尚待解決。Thomas等[5]采用對(duì)稱碰撞的方式研究了鐵在低于沖擊相變閾值下的層裂行為，并對(duì)鐵在低速?zèng)_擊下的Hugoniot 彈性極限與層裂強(qiáng)度進(jìn)行了分析；陳永濤等[6]采用等厚對(duì)稱碰撞實(shí)驗(yàn)，研究了純鐵在沖擊壓力超過(guò)相變閾值時(shí)的層裂行為，發(fā)現(xiàn)樣品中出現(xiàn)了二次層裂現(xiàn)象；翟少棟等[7]通過(guò)輕氣炮加載與激光加載兩種方式研究了鋁的層裂特性，結(jié)果表明鋁的層裂強(qiáng)度具有明顯的應(yīng)變率效應(yīng)；Koller 等[8]通過(guò)改變沖擊波波形，對(duì)無(wú)氧銅在不同沖擊波形式下的層裂特性進(jìn)行了研究，結(jié)果表明沖擊波波形與拉伸脈沖的持續(xù)時(shí)間會(huì)顯著影響無(wú)氧銅樣片中的層裂損傷演化。實(shí)驗(yàn)研究在宏觀尺度上提供了大量寶貴的實(shí)驗(yàn)數(shù)據(jù)，但由于其自身的特點(diǎn)，難以直接測(cè)量延性金屬內(nèi)部物理量隨時(shí)間的變化數(shù)據(jù)，只能通過(guò)如自由面速度曲線等間接數(shù)據(jù)分析材料內(nèi)部損傷演化過(guò)程。

隨著計(jì)算機(jī)的發(fā)展與應(yīng)用，數(shù)值模擬方法已經(jīng)成為實(shí)驗(yàn)研究的有力補(bǔ)充。目前在沖擊力學(xué)的數(shù)值模擬研究中主要有兩種方法，網(wǎng)格法與無(wú)網(wǎng)格法，其中無(wú)網(wǎng)格法以光滑粒子流體動(dòng)力學(xué)法（smootfied particle hydrodynamics SPH）[9]為代表得到了廣泛應(yīng)用。張鳳國(guó)等[10]對(duì)延性金屬在三角波加載下多次層裂破壞問(wèn)題進(jìn)行了數(shù)值模擬研究，對(duì)比分析了應(yīng)力瞬時(shí)斷裂準(zhǔn)則和Tuler-Butcher 準(zhǔn)則的差異，結(jié)果表明影響層裂片厚度的主要因素是材料自身的物理性質(zhì)和加載條件；種濤等[11]基于一維流體動(dòng)力學(xué)數(shù)值模擬方法，分析了鐵層裂損傷與沖擊相變之間的相互影響；Glam 等[12]采用數(shù)值模擬方法研究了溫度效應(yīng)對(duì)鋁的層裂強(qiáng)度與Hugonoit 彈性極限的影響，結(jié)果表明鋁的初始溫度與層裂強(qiáng)度正相關(guān)。Libersky 等[13]率先在SPH 方法中引入了材料強(qiáng)度效應(yīng)；徐金宏等[14]利用一種改進(jìn)SPH 方法對(duì)靶板厚度、彈丸速度和形狀對(duì)碎片云的影響進(jìn)行了研究；Zhou 等[15]在對(duì)鋁球超高速撞擊靶板的研究中，利用SPH 方法成功地進(jìn)行了數(shù)值模擬分析，結(jié)果與實(shí)驗(yàn)數(shù)據(jù)有較好的吻合性。賀年豐等[16]采用SPH 方法對(duì)爆轟條件下錫的層裂行為進(jìn)行了數(shù)值模擬，結(jié)果表明SPH方法得到的結(jié)果與實(shí)驗(yàn)數(shù)據(jù)有很好的一致性；可以看出，在宏觀尺度上，數(shù)值模擬方法與實(shí)驗(yàn)有很好的吻合性，并且數(shù)值模擬的加載范圍與條件更加靈活，計(jì)算快速、結(jié)果直觀，可以獲得材料宏觀尺度上的動(dòng)態(tài)破壞信息，但數(shù)值模擬結(jié)果的準(zhǔn)確定取決于采用的受狀態(tài)方程、強(qiáng)度模型和失效模型等因素，并且由于單元或粒子尺度影響，從微觀尺度研究層裂機(jī)理的能力有限。

在微觀尺度，分子動(dòng)力學(xué)方法（molecular dynamics,MD）已經(jīng)逐漸成為一種在微觀尺度研究材料性能的主流方法。席濤等[17]通過(guò)分子動(dòng)力學(xué)方法研究分析了超高應(yīng)變率下銅的層裂特性，獲得了銅在109～1010s?1時(shí)的層裂強(qiáng)度；Rawat 等[18]研究了應(yīng)變率對(duì)單晶鐵中的損傷演化的影響，結(jié)果表明隨著應(yīng)變率的增加，空洞更容易成核，但在低應(yīng)變率條件下空洞的生長(zhǎng)速度更快；Yang 等[19]研究了應(yīng)變率、溫度、晶粒尺寸等因素對(duì)鋁動(dòng)態(tài)損傷發(fā)展的影響，揭示了不同影響因素下?lián)p傷發(fā)展的過(guò)程；Chen 等[20]通過(guò)分子動(dòng)力學(xué)方法研究了晶界特性對(duì)動(dòng)態(tài)損傷的影響，結(jié)果表明損傷分布與晶界取向和空洞形核應(yīng)力相關(guān)。可以看出：分子動(dòng)力學(xué)模擬可以揭示動(dòng)態(tài)損傷的微觀機(jī)理，給出材料內(nèi)部應(yīng)力與損傷演化信息，有助于從根本上了解金屬材料的動(dòng)態(tài)損傷機(jī)制，但受到計(jì)算能力的限制，無(wú)法在全尺寸上復(fù)現(xiàn)層裂現(xiàn)象[21-23]。

典型自由面速度曲線如圖1（b）所示，從中可以分析得到延性金屬材料動(dòng)態(tài)損傷的宏觀響應(yīng)的一系列重要信息，如加載應(yīng)力幅值、拉伸應(yīng)變率、層裂強(qiáng)度和層裂片厚度等，因此自由面速度曲線是研究層裂演化過(guò)程的最重要參考數(shù)據(jù)之一[24]。實(shí)際上延性金屬的層裂過(guò)程十分復(fù)雜，是一種內(nèi)部損傷隨時(shí)空演化的動(dòng)力學(xué)過(guò)程，材料從受到拉伸應(yīng)力影響開始直至完全破壞要經(jīng)歷一個(gè)損傷累積的過(guò)程，期間會(huì)伴隨能量的耗散和性能的退化，這都會(huì)影響材料內(nèi)部波的傳播過(guò)程，從而影響自由面速度曲線的形式。因此，自由面速度曲線是微觀上的損傷演化過(guò)程和宏觀響應(yīng)場(chǎng)之間相互作用的一種宏觀表象，由于宏觀尺度上的實(shí)驗(yàn)和數(shù)值模擬很難得到反應(yīng)內(nèi)部損傷演化的信息，這對(duì)充分認(rèn)識(shí)宏觀響應(yīng)與微觀損傷發(fā)展之間的關(guān)系造成了阻礙，也就導(dǎo)致對(duì)自由面速度曲線中的一些特征理解存在爭(zhēng)議。裴曉陽(yáng)等[2]基于理論分析和微觀損傷演化動(dòng)力學(xué)理論，對(duì)延性金屬層裂自由面速度曲線的某些特征所對(duì)應(yīng)的物理內(nèi)涵進(jìn)行了闡述，定性地指出了宏觀上自由面速度曲線的響應(yīng)特征與內(nèi)部損傷演化的對(duì)應(yīng)關(guān)系，但是并沒有從微觀尺度上的給出材料層裂過(guò)程中的損傷演化過(guò)程，缺少在微觀尺度的機(jī)理分析與驗(yàn)證。

目前的研究大多只局限于單一尺度下層裂現(xiàn)象模擬或微觀損傷演化分析，少有結(jié)合宏觀與微觀尺度下對(duì)層裂自由面速度曲線特征的多尺度視角下的研究，缺乏對(duì)自由面速度曲線的微觀視角解析。本文以延性金屬鉭為研究對(duì)象，在宏觀尺度上對(duì)鉭在高速?zèng)_擊下的層裂行為進(jìn)行數(shù)值模擬，通過(guò)與實(shí)驗(yàn)數(shù)據(jù)的比較，驗(yàn)證模型的合理性；在微觀制度上通過(guò)分子動(dòng)力學(xué)方法分析鉭在層裂過(guò)程中的損傷演化過(guò)程。進(jìn)而將宏觀尺度與微觀尺度的模擬結(jié)果有機(jī)結(jié)合起來(lái)，從多尺度視角對(duì)延性金屬鉭的層裂行進(jìn)行研究。揭示了自由面速度曲線上的典型特征所蘊(yùn)含的損傷演化規(guī)律和及物理內(nèi)涵，研究結(jié)果可以為全面了解層裂這一復(fù)雜的動(dòng)力學(xué)行為提供參考。

1 計(jì)算模型與方法

為了便于與實(shí)驗(yàn)數(shù)據(jù)進(jìn)行對(duì)比驗(yàn)證，宏觀尺度全尺寸模型參照平板撞擊實(shí)驗(yàn)建立[25]，選取樣片自由面中心位置數(shù)據(jù)繪制自由面速度曲線，如圖2（a）所示；微觀尺度分子動(dòng)力學(xué)模型選取樣片中心拉伸區(qū)域進(jìn)行模擬，MD模型如圖2（b）所示。

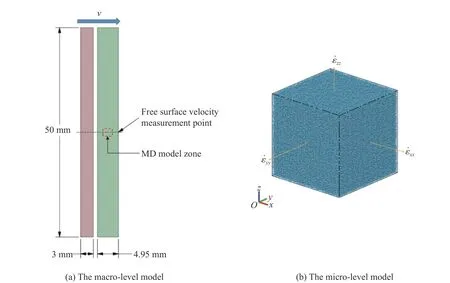
圖2 多尺度模擬模型示意圖Fig.2 Configurations of the multi-scale simulation models

1.1 宏觀尺度數(shù)值模擬

1.1.1狀態(tài)方程與材料本構(gòu)

Mie-Grüneisen 狀態(tài)方程能夠較為準(zhǔn)確地描述金屬在沖擊載荷下的動(dòng)力學(xué)行為，其表達(dá)式如下[16]：

式中：ρ為沖擊后材料密度，ρ0為初始材料密度，S1為材料常數(shù)，γ 為Grüneisen 系數(shù)，e為質(zhì)量?jī)?nèi)能。Mie-Grüneisen 狀態(tài)方程參數(shù)如表1所示[26]。

表1 Mie-Grüneisen 狀態(tài)方程參數(shù)Table 1 Parameters for Mie-Grüneisen equation of state

考慮了三種常用的描述延性金屬在強(qiáng)動(dòng)載荷下的動(dòng)態(tài)破壞行為的模型，分別是Johnson-Cook（JC）模型[27]、Steinberg-Cochran-Guinan（SCG）模型[28]以及Zerilli-Armstrong（ZA）模型[29]。

（1）JC模型

JC模型假設(shè)材料各向同性，綜合考慮了應(yīng)變、應(yīng)變率硬化和溫升軟化等因素，并且將應(yīng)變、應(yīng)變率硬化效應(yīng)和溫升軟化效應(yīng)解耦，JC模型的表達(dá)式為：

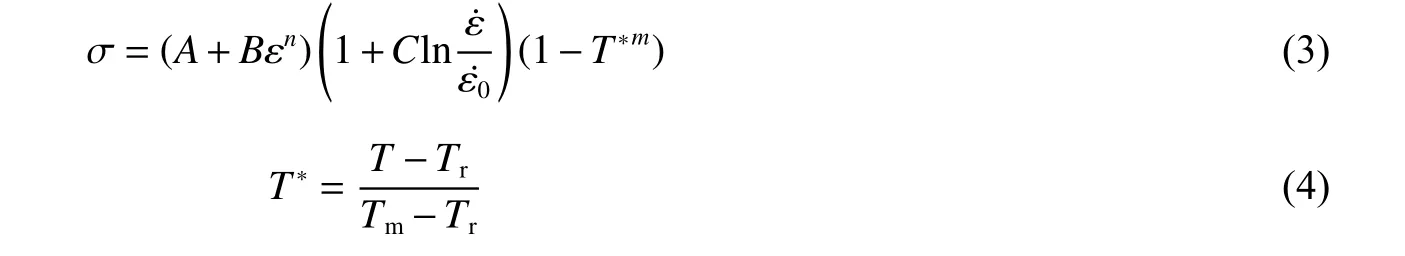
式中：A、B、C、n、m為材料常數(shù)，Tr為參考溫度，Tm為材料融化溫度，ε˙0為參考應(yīng)變率。JC模型參數(shù)如表2所示[30]。

表2 Johnson-Cook 模型參數(shù)Table2 Parameters for the Johnson-Cook model

（2）ZA 模型

基于熱激活和位錯(cuò)動(dòng)力學(xué)理論，Zerilli等[29]提出了一種描述體心立方金屬（BCC）的強(qiáng)度模型，考慮了溫度、應(yīng)變率與溫度的影響，ZA 模型的表達(dá)式為：

式中：C0、k1、C2、C3、C4、C5為材料常數(shù)，T為絕對(duì)溫度，ε 為塑性應(yīng)變，λ 為晶粒尺寸。ZA 模型參數(shù)如表3所示[29]。

表3 Zerilli-Armstrong 模型參數(shù)Table 3 Parameters for the Zerilli-Armstrong model

（3）SCG 模型

Steinberg 等[28]提出的SCG 模型考慮了靜水壓力對(duì)剪切模量和屈服強(qiáng)度的強(qiáng)化效應(yīng)以及溫度軟化效應(yīng)，同時(shí)忽略了應(yīng)變率效應(yīng)，并假設(shè)金屬在融化狀態(tài)下可以忽略材料強(qiáng)度。屈服強(qiáng)度Y和剪切模量G分別為：

式中：Ymax為最大屈服強(qiáng)度。SCG 模型參數(shù)如表4所示[28]。

表4 Steinberg-Cochran-Guinan 模型參數(shù)Table 4 Parameters for the Steinberg-Cochran-Guinan model

1.1.2層裂模型

Grady[31]基于斷裂力學(xué)理論提出了層裂的能量平衡破碎模型，將層裂強(qiáng)度ps與層裂碎片平均尺寸和應(yīng)變率聯(lián)系起來(lái)。對(duì)于延性金屬，層裂強(qiáng)度隨沖擊加載過(guò)程而改變，表達(dá)式為[32]：

式中：ρ為材料密度，Y為屈服強(qiáng)度，c0為材料體積聲速，εc為材料臨界失效應(yīng)變，對(duì)金屬材料一般可取為0.15[31]。

1.2 自由面速度曲線分析

層裂強(qiáng)度是表征材料在強(qiáng)動(dòng)載荷下性能的一個(gè)重要指標(biāo)，在材料動(dòng)態(tài)損傷研究中具有重要參考意義。Novikov[33]基于聲學(xué)近似的方法給出了計(jì)算層裂強(qiáng)度的公式：

式中：ρ0為材料初始密度，cb為材料初始體聲速，Δus為自由面速度曲線最大值與第一次速度拉回時(shí)的差值。

層裂區(qū)域平均拉伸應(yīng)變率ε˙s的計(jì)算公式為[34]：

式中：Δus與Δts分別為自由面上速度最大值和第一個(gè)極小值之間的速度差和時(shí)間差。

自由面速度回跳速率，即極小值到峰值速度之間的斜率，計(jì)算公式為：

式中：Δur與Δtr分別為自由面上速度第一個(gè)極小值與其后峰值之間的速度差和時(shí)間差。

層裂片厚度h為：

式中：Δt為第一個(gè)層裂振蕩周期持續(xù)時(shí)間，cl為彈性縱波聲速。

1.3 微觀尺度MD模型

鉭原子間的相互作用采用Ravelo等[35]提出的嵌入原子勢(shì)函數(shù)，MD模擬基于Lammps 軟件[36]進(jìn)行。MD模型尺寸為16.53 nm×16.53 nm×16.53 nm，共250000個(gè)原子，在模型x、y、z方向施加周期性邊界條件。加載之前采用NPT 系綜對(duì)模型進(jìn)行30 ps的弛豫，確保體系在施加荷載之前處于平衡狀態(tài)；加載過(guò)程采用NVE 系綜，在x、y、z方向施加相等的應(yīng)變率，為了保持與宏觀尺度模擬的一致性，施加應(yīng)變率數(shù)值與宏觀尺度模型中的拉伸應(yīng)變率相同。

2 宏觀尺度模型驗(yàn)證

分別采用Lagrange網(wǎng)格法與SPH無(wú)網(wǎng)格法結(jié)合三種強(qiáng)度模型對(duì)鉭的層裂進(jìn)行了模擬，并對(duì)二者得到的結(jié)果進(jìn)行了比較分析。表5中列出了用于驗(yàn)證的模型尺寸參數(shù)、撞擊速度、強(qiáng)度模型等信息。模型為二維軸對(duì)稱，Lagrange 網(wǎng)格尺寸為0.05 mm，SPH 粒子尺寸為0.1 mm，樣片直徑為50 mm，撞擊速度為306 m/s。

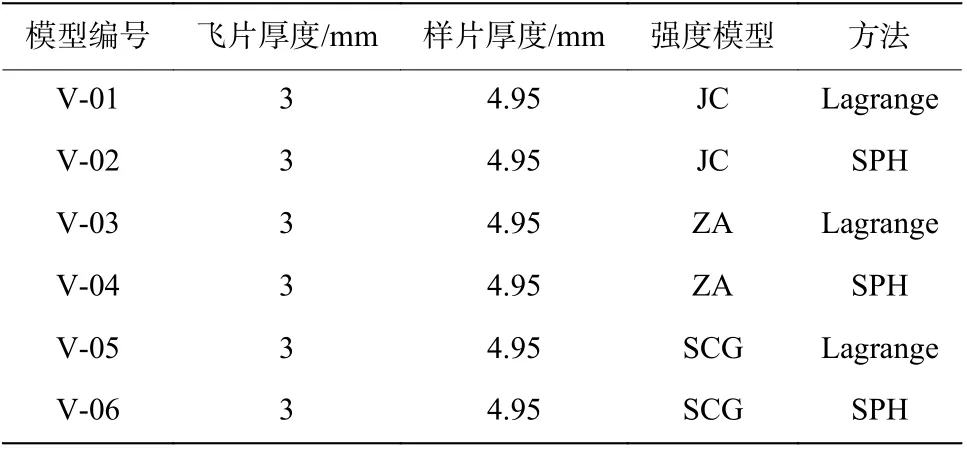
表5 用于驗(yàn)證的模型編號(hào)及參數(shù)設(shè)置Table 5 Model number and parameter settings for validation

不同模型得到的自由面速度曲線如圖3所示。從模擬結(jié)果與實(shí)驗(yàn)數(shù)據(jù)對(duì)比可以發(fā)現(xiàn)，Lagrange 網(wǎng)格法與SPH 無(wú)網(wǎng)格法在數(shù)值模擬中各有優(yōu)勢(shì)，在0～2μs時(shí)，樣片自由面速度曲線速度由0 m/s增加到最大值，Lagrange方法得到的模擬結(jié)果與實(shí)驗(yàn)數(shù)據(jù)有較好的吻合性，并且Lagrange 方法得到的結(jié)果可以觀察到明顯的Hugoniot 彈性極限信號(hào)，而由SPH 方法得到的結(jié)果Hugoniot 彈性極限信號(hào)不是特別明顯；在自由面速度開始下降后，Lagrange方法得到的模擬結(jié)果中自由面速度回拉速率比實(shí)驗(yàn)數(shù)據(jù)更快，SPH方法得到的結(jié)果與實(shí)驗(yàn)數(shù)據(jù)較為吻合。結(jié)果表明采用SPH 無(wú)網(wǎng)格法在鉭層裂模擬中是可行的，結(jié)合兩種方法可以得到完整的自由面速度曲線數(shù)據(jù)。此外，結(jié)果表明SCG 模型在鉭的層裂模擬中更為適合。

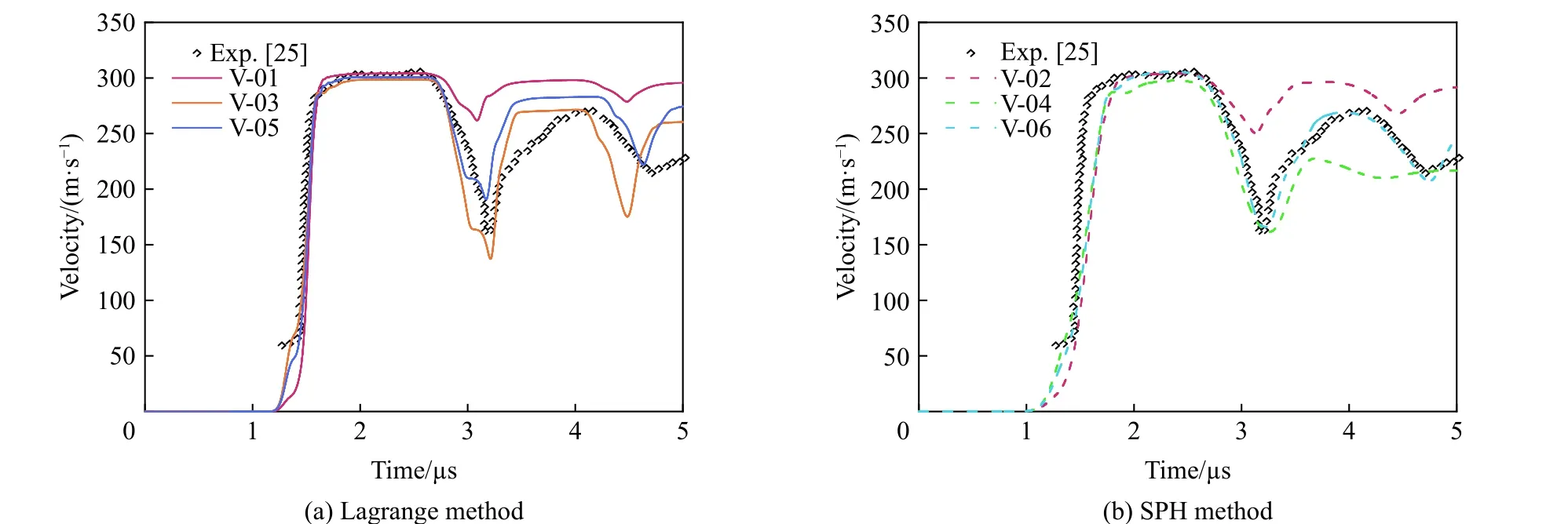
圖3 不同模型的自由面速度曲線與實(shí)驗(yàn)數(shù)據(jù)[25]對(duì)比Fig.3 Comparison of free-surface velocity profiles by different models with experiment data[25]

為了分析不同加載應(yīng)變率下的層裂特性，通過(guò)改變加載條件改變了層裂區(qū)域的拉伸應(yīng)變率，表6給出了模型加載條件參數(shù)，拉伸應(yīng)變率范圍為2.13×104～5.40×104s?1，壓力范圍為6.19～12.25 GPa。不同拉伸應(yīng)變率下的鉭層裂宏觀尺度數(shù)值模擬結(jié)果如圖4所示，從圖中可以看出，自由面最大速度與飛片撞擊速度基本相同；在相同的加載速度下，通過(guò)改變飛片厚度自由面速度平臺(tái)寬度也隨之改變，二者之間呈現(xiàn)正比關(guān)系，飛片厚度越大，自由面速度曲線平臺(tái)寬度越寬。

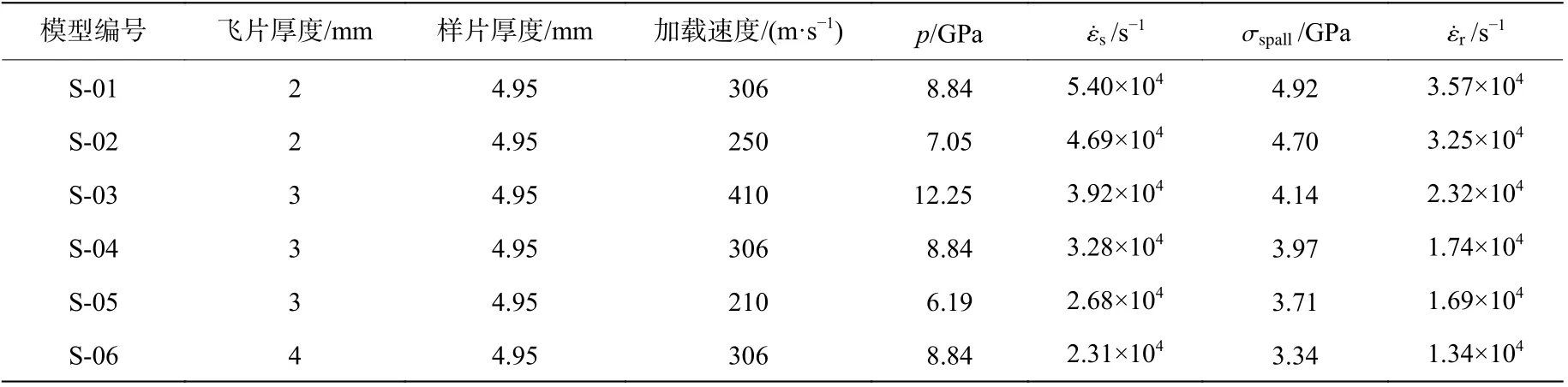
表6 不同應(yīng)變率下平面撞擊層裂模型參數(shù)與結(jié)果Table 6 Parametersof planar plateimpact simulationsand resultsunder various strain rates

圖4 宏觀尺度下不同拉伸應(yīng)變率自由面速度曲線Fig.4 Free surface velocity under various tensile strain rates at macro-scale

3 結(jié)果分析

3.1 層裂強(qiáng)度

層裂強(qiáng)度是金屬材料動(dòng)態(tài)損傷行為的重要參數(shù)之一，通過(guò)對(duì)模擬結(jié)果的分析同時(shí)參照文獻(xiàn)[3]給出的銅層裂強(qiáng)度與拉伸應(yīng)變率的關(guān)系σspall=0.15ε˙0.2，我們得到了鉭的層裂強(qiáng)度與拉伸應(yīng)變率之間的關(guān)系：

圖5給出了鉭的層裂強(qiáng)度與拉伸應(yīng)變率的關(guān)系，從圖中可以發(fā)現(xiàn)，層裂強(qiáng)度不是一個(gè)僅受到加載速度影響的物理量，在加載速度相同的條件下，S-06、S-04、S-01的層裂強(qiáng)度隨著拉伸應(yīng)變率的升高而增加，對(duì)于S-05、S-03、S-02盡管加載速度相差較大，但是同樣表現(xiàn)出層裂強(qiáng)度與拉伸應(yīng)變率之間的正比關(guān)系。這表明層裂強(qiáng)度呈現(xiàn)出一種率相關(guān)特性，即隨拉伸應(yīng)變率的增長(zhǎng)而增加。

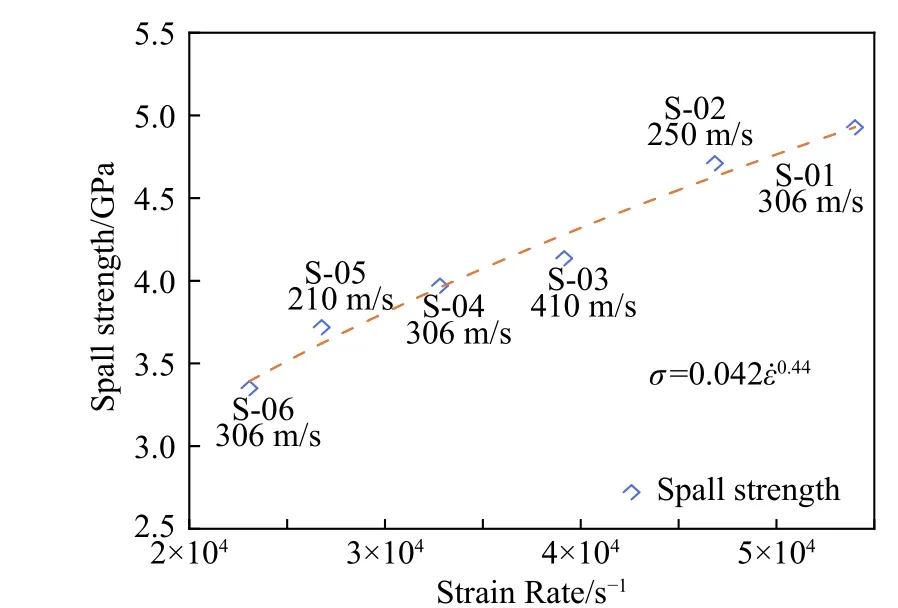
圖5 層裂強(qiáng)度與拉伸應(yīng)變率關(guān)系Fig.5 Relationship between spall strength and tensile strain rate

圖6給出了對(duì)數(shù)坐標(biāo)下σspall與ε˙s之間的關(guān)系，從圖中可以看出在對(duì)數(shù)坐標(biāo)下層裂強(qiáng)度表現(xiàn)出了明顯的率相關(guān)特性。我們對(duì)比了更高拉伸應(yīng)變率下的實(shí)驗(yàn)數(shù)據(jù)[37]，更高的拉伸應(yīng)變率下層裂強(qiáng)度同樣是隨應(yīng)變率提高而增加，同時(shí)這也驗(yàn)證了數(shù)值模擬結(jié)果的準(zhǔn)確性。

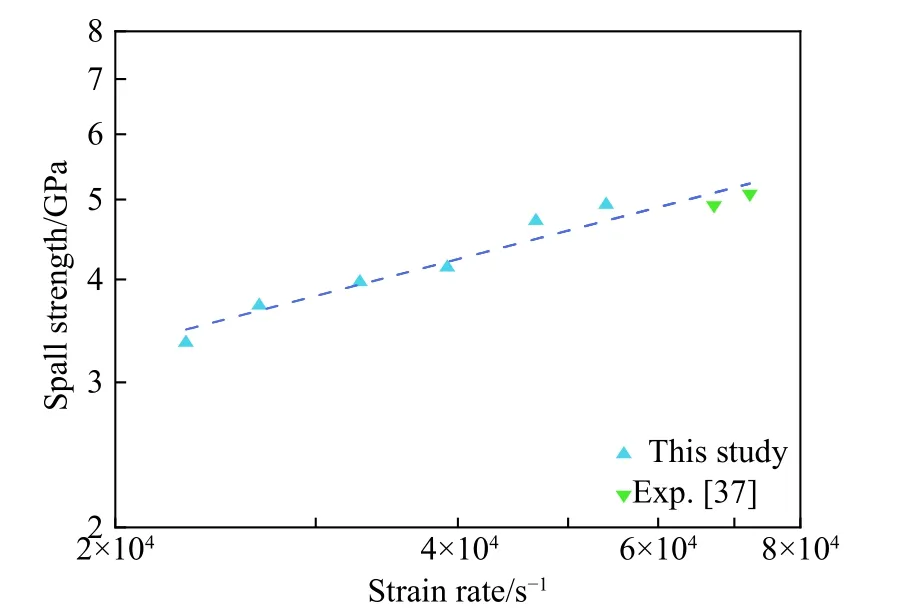
圖6 對(duì)數(shù)坐標(biāo)下層裂強(qiáng)度與拉伸應(yīng)變率的關(guān)系Fig.6 Relationship between spall strength and tensilestrain rate in logarithmic coordinates

前文分析中的層裂強(qiáng)度是根據(jù)式（11）進(jìn)行計(jì)算得到的，也是目前研究中廣泛采用的聲學(xué)近似計(jì)算方法，但并不是唯一的計(jì)算方法。Stepanov[33]指出，對(duì)于延性金屬，平板撞擊過(guò)程中沖擊應(yīng)以彈性縱波速度cl傳播。而在它前面的入射稀疏塑性波應(yīng)以體積聲速cb傳播，當(dāng)重點(diǎn)考慮彈性波的影響時(shí)，有效聲速ce為：

據(jù)此，可得到層裂強(qiáng)度的一種修正形式：

式中：ρ0為材料密度，?u為自由面上速度最大值和第一個(gè)極小值之間的速度差。除此之外，Kanel[38]指出在層裂強(qiáng)度計(jì)算中還應(yīng)考慮層裂片厚度影響，當(dāng)計(jì)及層裂片厚度影響時(shí)：

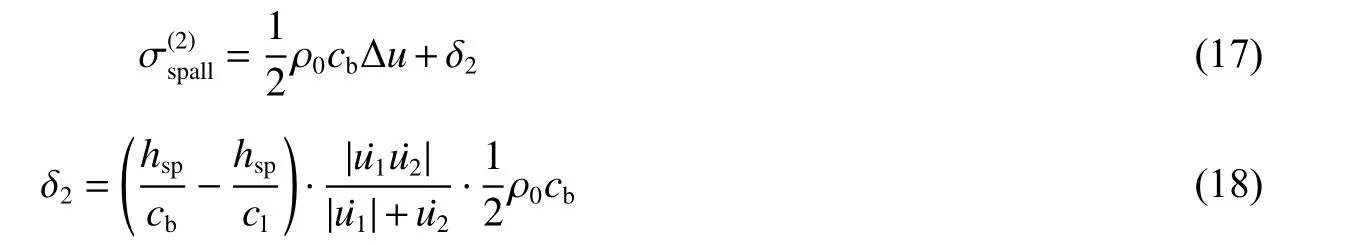
式中：u˙1為樣品自由面速度-時(shí)間曲線上Pullback 信號(hào)出現(xiàn)前的速度變化率，u˙2為層裂反彈信號(hào)的速度變化率，hsp為層裂片厚度。由3種公式計(jì)算得到的層裂強(qiáng)度如表7所示，分析發(fā)現(xiàn)式（17）與式（11）得到的結(jié)果最大相差8%，式（18）與式（17）得到的結(jié)果相差不大。表明通過(guò)自由面速度曲線來(lái)計(jì)算層裂強(qiáng)度與選用的計(jì)算方法相關(guān)，而且不同計(jì)算模型之間存在一定差異，在分析時(shí)應(yīng)該得到關(guān)注。

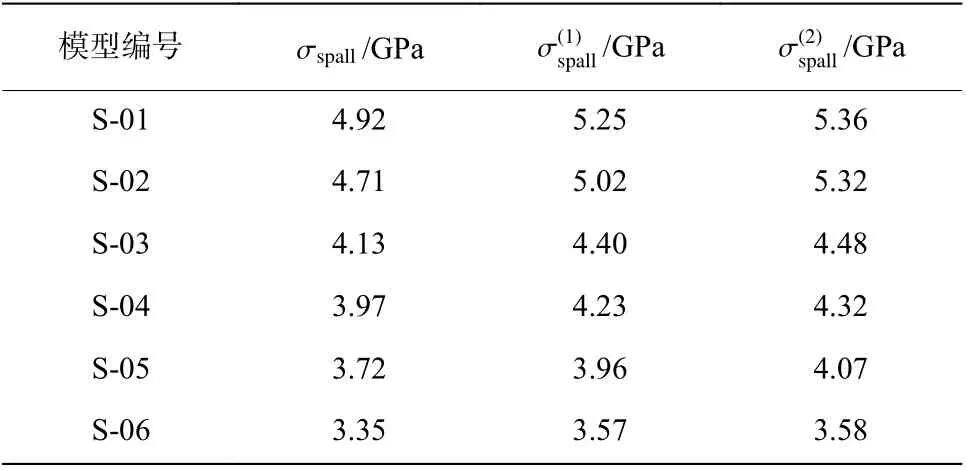
表7 不同計(jì)算公式得到的層裂強(qiáng)度Table7 Spall strengths obtained by different formulas

3.2 自由面速度曲線特征多尺度分析

從宏觀尺度下層裂特性的分析可以看出，自由面速度曲線反映了層裂過(guò)程中材料內(nèi)部損傷演化與宏觀響應(yīng)場(chǎng)的相互作用，全面和準(zhǔn)確地認(rèn)識(shí)自由面速度曲線對(duì)研究層裂現(xiàn)象具有重要的意義。基于目前的研究手段，對(duì)層裂過(guò)程中損傷演化的原位觀測(cè)依然難以實(shí)現(xiàn)，無(wú)法直觀的準(zhǔn)確的了解層裂過(guò)程中材料的宏觀動(dòng)力學(xué)響應(yīng)與微結(jié)構(gòu)演化之間的關(guān)系，進(jìn)而導(dǎo)致對(duì)自由面速度曲線的理解也存在一些爭(zhēng)議，例如：Pullback 信號(hào)的意義、損傷演化的形式、回跳速率的意義等。針對(duì)以上幾個(gè)方面的問(wèn)題，通過(guò)分子動(dòng)力學(xué)方法給出層裂過(guò)程中損傷演化的情況，定性的從微觀尺度對(duì)自由面速度曲線上的一些典型特征進(jìn)行解讀。

3.2.1 Pullback 信號(hào)

Pullback 信號(hào)是用來(lái)判斷層裂是否發(fā)生的重要依據(jù)，但此時(shí)材料是否完全分離尚存爭(zhēng)議。Zurek 等[39]認(rèn)為Pullback 信號(hào)出現(xiàn)時(shí)材料已經(jīng)完全分離，但Kanel等[40]等觀察到在層裂面損傷很小時(shí)，依然有Pullback 信號(hào)出現(xiàn)；Bonora 等[2]認(rèn)為Pullback 信號(hào)的出現(xiàn)與微孔洞成核相關(guān)，但未給出驗(yàn)證。下文以S-04加載情況為例，對(duì)其自由面速度曲線中Pullback 信號(hào)意義從微觀尺度進(jìn)行了分析。

圖7～8給出了自由面速度下降后的時(shí)程曲線與層裂區(qū)MD模型內(nèi)部應(yīng)力及損傷演化情況，在分析中考慮了自由面速度曲線中Pullback 信號(hào)在選取時(shí)的誤差，將Pullback 信號(hào)出現(xiàn)時(shí)間擴(kuò)展為0.05μs時(shí)間范圍進(jìn)行分析。從圖7中可以看出，在Pullback 出現(xiàn)的時(shí)間范圍內(nèi)，層裂區(qū)域內(nèi)的應(yīng)力達(dá)到峰值，在經(jīng)過(guò)Pullback 信號(hào)后，層裂區(qū)域內(nèi)的應(yīng)力迅速下降，出現(xiàn)應(yīng)力松弛；對(duì)比此時(shí)層裂區(qū)域內(nèi)的損傷發(fā)展可以發(fā)現(xiàn)，Pullback 信號(hào)出現(xiàn)的時(shí)間范圍對(duì)應(yīng)的是損傷發(fā)展的初始階段，也就是微孔洞成核階段。在圖8中可以直觀的觀察到內(nèi)部損傷演化的情況，可以看出，在Pullback 信號(hào)時(shí)間內(nèi)微孔洞開始逐漸產(chǎn)生，此時(shí)內(nèi)部孔洞體積占比非常小，這都表明鉭在Pullback 信號(hào)出現(xiàn)的時(shí)間范圍內(nèi)層裂區(qū)域?qū)嶋H上并未完全分離，而且Pullback 信號(hào)對(duì)應(yīng)的實(shí)際上是內(nèi)部微孔洞形核的過(guò)程，從微觀尺度證明了Bonora 等[2]的推測(cè)。此外，在通過(guò)自由面速度曲線計(jì)算層裂強(qiáng)度時(shí)，Pullback 對(duì)應(yīng)的速度降低幅值（圖1b中Δu）是一個(gè)重要的依據(jù)，通過(guò)前面的分析表明在鉭的層裂中自由面速度曲線Pullback 信號(hào)對(duì)應(yīng)的是微孔洞形核的過(guò)程，這表明Δu實(shí)際上反映了了微孔洞形核的條件，那么通過(guò)Δu得到的層裂強(qiáng)度更準(zhǔn)確地說(shuō)應(yīng)該是抵抗損傷起源的強(qiáng)度或微孔洞成核的一種表征。

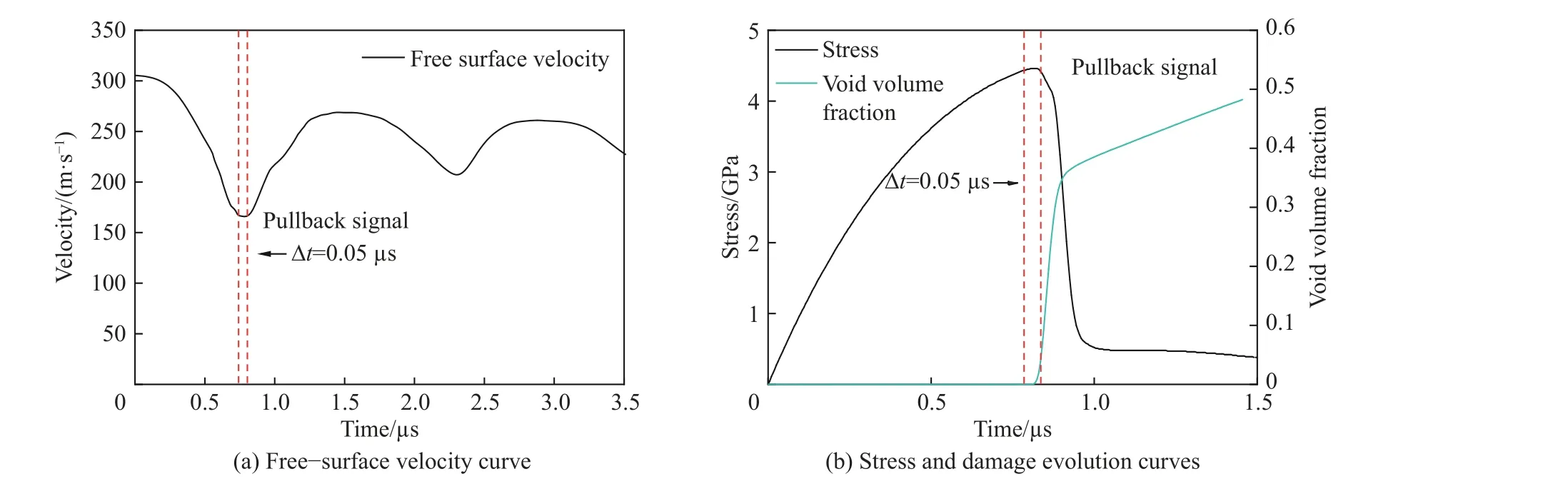
圖7 Pullback 信號(hào)及其對(duì)應(yīng)的MD模型應(yīng)力與空洞演化情況Fig.7 Pullback signal and the stress and void volume evolution in the MD model

層裂區(qū)域的損傷演化在宏觀尺度的試驗(yàn)下難以直接觀測(cè)，借助微觀尺度的MD模型，可以從微觀尺度對(duì)鉭層裂過(guò)程中的損傷演化進(jìn)程進(jìn)行分析。在圖9～11中我們給出了損傷演化過(guò)程中內(nèi)部孔洞所占體積分?jǐn)?shù)、微孔洞數(shù)量與內(nèi)部孔洞情況。從圖9中可以看出層裂區(qū)域內(nèi)微損傷的演化可以分為3 個(gè)階段：孔洞形核（S1）、長(zhǎng)大（S2）與聚集（S3）。在內(nèi)部壓力達(dá)到峰值附近時(shí)，微孔洞開始形核，此時(shí)孔洞數(shù)量快速增加，但是孔洞體積占比非常小，在S1階段空洞數(shù)量演化情況如圖10所示；隨后進(jìn)入孔洞長(zhǎng)大階段，此時(shí)應(yīng)力開始快速下降，而應(yīng)力松弛意味著出現(xiàn)能量耗散，耗散的能量為孔洞長(zhǎng)大提供動(dòng)力，孔洞的快速增長(zhǎng)導(dǎo)致孔洞占比迅速升高，孔洞數(shù)量在這個(gè)階段開始降低，這表明在S2階段中孔洞體積的增加是由于孔洞長(zhǎng)大所致，而不是新孔洞出現(xiàn)造成的；在應(yīng)力下降到穩(wěn)定狀態(tài)后，孔洞開始進(jìn)入聚集階段，此時(shí)孔洞體積占比增長(zhǎng)速度降低，并且孔洞數(shù)量趨于穩(wěn)定，這表明在損傷發(fā)展后期是層裂區(qū)域內(nèi)大孔洞再聚集最終導(dǎo)致層裂的過(guò)程，S2階段的空洞長(zhǎng)大與S3階段的空洞聚集過(guò)程如圖11所示。

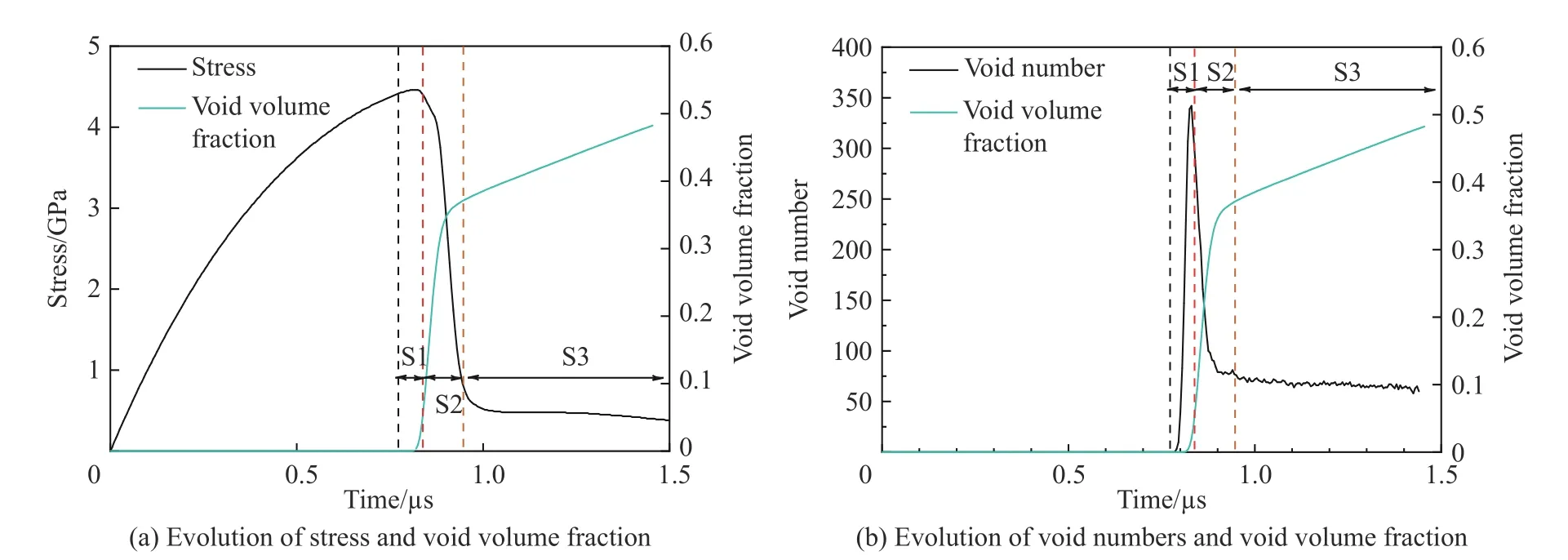
圖9 空洞體積演化與應(yīng)力及空洞數(shù)量的關(guān)系Fig.9 Relationship of the evolution of void volume with stress and void numbers

圖10 階段1的空洞數(shù)量演化情況Fig.10 Void number evolution during stage 1

圖11 階段2與3的空洞長(zhǎng)大與聚集情況Fig.11 Void growing and coalescence during stage2 and stage 3

3.2.2回跳速率

在以往的分析中，往往只是關(guān)注Pullback 信號(hào)及其前段自由面速度曲線，對(duì)Pullback 信號(hào)出現(xiàn)后的自由面速度回跳曲線少有涉及。以自由面速度曲線中Pullback 信號(hào)為起點(diǎn)，分析了自由面速度回跳曲線的變化情況，不同應(yīng)變率條件下的自由面速度回跳曲線如圖12所示。從圖中可以看出，自由面速度回跳曲線隨加載速度和飛片厚度沒有明顯的變化趨勢(shì)，但是隨著拉伸應(yīng)變率的增加，曲線逐漸變得陡峭，斜率逐漸增加。

圖12 自由面速度回跳曲線Fig.12 Free surface velocity curve from spall signal

圖13給出了層裂強(qiáng)度與回跳速率之間的關(guān)系。可以看出，層裂強(qiáng)度與回跳速率之間近似呈線性增長(zhǎng)的關(guān)系，而層裂強(qiáng)度具有率相關(guān)特性，這表明自由面速度回跳曲線也與應(yīng)變率相關(guān)。

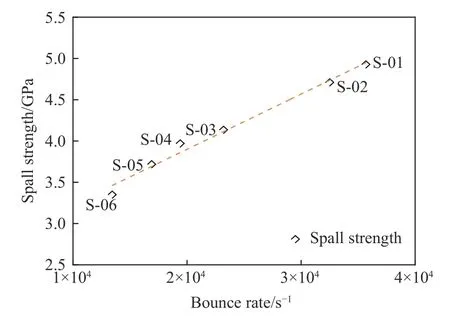
圖13 層裂強(qiáng)度與回跳速率的關(guān)系Fig.13 Relationship between spalling strength and rebound rate

自由面速度回跳與拉伸應(yīng)變率的關(guān)系如圖14所示。從圖14中可以看出，自由面速度回跳速率隨著拉伸應(yīng)變率的升高而增長(zhǎng)，二者近似呈線性變化趨勢(shì)。因此，可以推斷鉭在層裂過(guò)程中樣片內(nèi)部的損傷演化速率也是隨拉伸應(yīng)變率的增長(zhǎng)而增加。

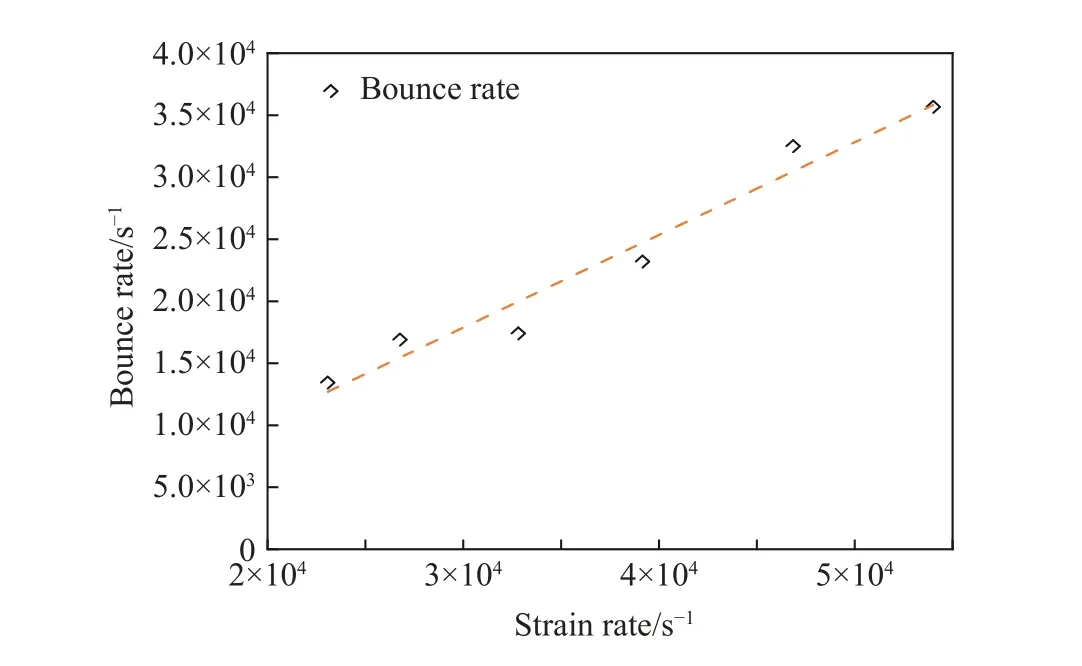
圖14 不同拉伸應(yīng)變率下自由面速度回跳速率Fig.14 Free surface bounce rate under various tensile strain rates

從圖9中發(fā)現(xiàn)Pullback 信號(hào)后自由面速度回跳時(shí)間段內(nèi)層裂區(qū)域內(nèi)損傷快速增長(zhǎng)的階段，微孔洞體積占比迅速增加，這表明自由面速度回跳與損傷演化之間存在對(duì)應(yīng)關(guān)系。Kanel 等[40]基于特征線方法分析了回跳速率和損傷演化速率的關(guān)系，指出二者之間是正比關(guān)系。圖15給出了層裂區(qū)域內(nèi)不同應(yīng)變率下應(yīng)力演化的情況，不同應(yīng)變率下?lián)p傷演化的情況如圖16所示。

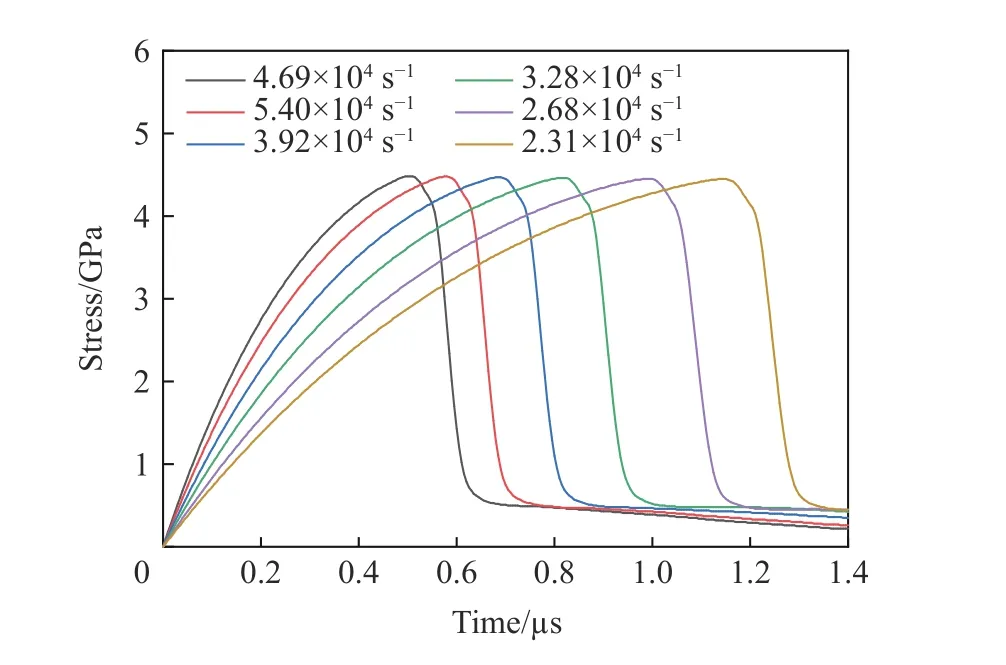
圖15 不同應(yīng)變率下應(yīng)力時(shí)程曲線Fig.15 Histories of stress under different strain rates

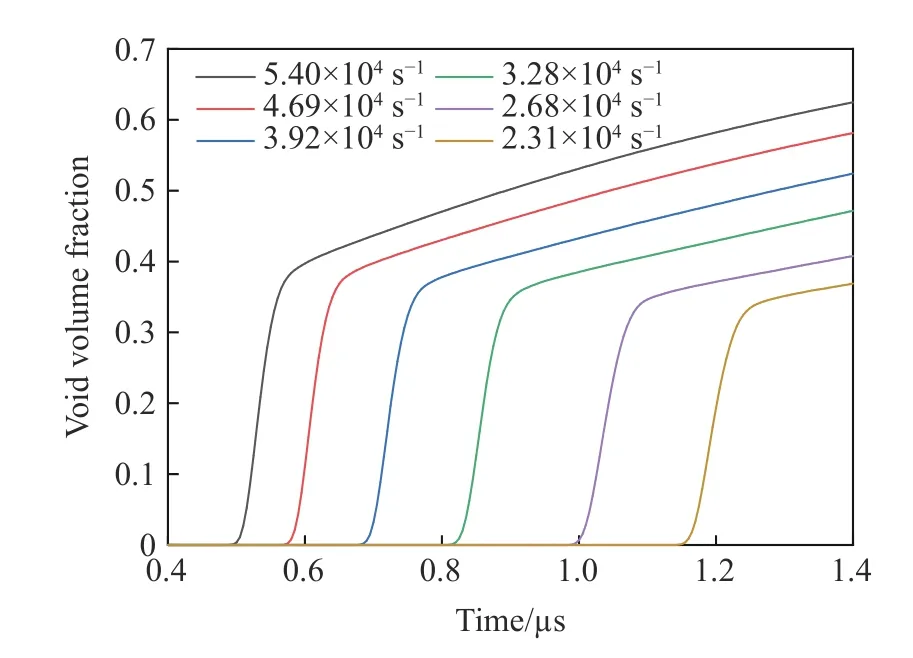
圖16 不同應(yīng)變率下?lián)p傷演化情況Fig.16 Damage evolution under different strain rates

從前文的分析中，我們發(fā)現(xiàn)回跳速率與拉伸應(yīng)變率二者近似呈線性變化趨勢(shì)，拉伸應(yīng)變率越高，回跳速率越大。不同應(yīng)變率下應(yīng)力演化情況如圖15所示，從宏觀上波系分析可知自由面速度回跳速率與應(yīng)力松弛速度相關(guān)，從層裂區(qū)域中的應(yīng)力變化情況可以發(fā)現(xiàn)，應(yīng)力下降速度隨應(yīng)變率的升高而加快，這表明回跳速率與應(yīng)力松弛速度是呈正相關(guān)的。應(yīng)力松弛速度越快，代表能量耗散的速度越快，而能量耗散的速度與損傷演化的速度相關(guān)。圖16給出了不同應(yīng)變率下?lián)p傷演化的情況，可以明顯看出隨著應(yīng)變率的增加，微孔洞在長(zhǎng)大階段的速度越來(lái)越快。綜上所述，自由面速度回跳速率是層裂區(qū)域損傷演化速率的宏觀表征。

4 結(jié) 論

本文以延性金屬鉭為研究對(duì)象，通過(guò)改變飛片厚度與加載速度改變加載應(yīng)變率，對(duì)不同加載條件下的自由面速度曲線特性進(jìn)行了分析。重要的是，結(jié)合宏觀和微觀尺度視角揭示了自由面速度曲線與微損傷演化之間的聯(lián)系，特別是對(duì)自由面速度曲線上的一些典型特征的物理內(nèi)涵從微觀尺度進(jìn)行了解讀，結(jié)果表明：

（1）對(duì)鉭層裂的宏觀尺度模擬中，Lagrange方法在模擬鉭的彈塑性轉(zhuǎn)變過(guò)程有較好的表現(xiàn)，能夠觀測(cè)到明顯的Hugoniot 彈性極限信號(hào)，SPH 方法得到的結(jié)果與實(shí)驗(yàn)數(shù)據(jù)更為符合，能夠較為準(zhǔn)確地描述層裂全過(guò)程中的自由面速度曲線變化情況，證明SPH 方法研究鉭的層裂行為是可行的；

（2）在宏觀尺度上，鉭的層裂強(qiáng)度隨加載應(yīng)變率的升高而增加，二者近似呈指數(shù)關(guān)系；分析表明，層裂強(qiáng)度與回跳速率之間存在正比關(guān)系，表明自由面速度回跳速率也是層裂行為的一種反映，應(yīng)該得到關(guān)注；通過(guò)觀察發(fā)現(xiàn)了回跳速率與拉伸應(yīng)變率之間近似為線性關(guān)系，隨拉伸應(yīng)變率的升高而增長(zhǎng)。

（3）微觀尺度分析表明，自由面速度曲線是層裂區(qū)域內(nèi)的微孔洞形核、長(zhǎng)大、聚集直至完全斷裂的微損傷演化過(guò)程的宏觀反映。Pullback 信號(hào)的臨界點(diǎn)是微孔洞的形核在宏觀上的表征，自由面速度曲線在Pullback 信號(hào)前的下降幅值代表了微孔洞形核的條件，而由此計(jì)算得到的層裂強(qiáng)度反映了微孔洞形核強(qiáng)度，Pullback 信號(hào)后速度回跳速率反映了層裂區(qū)域內(nèi)損傷演化的速率。