基于神經(jīng)網(wǎng)絡(luò)與馬爾可夫組合模型的視頻流行度預(yù)測算法

馬學(xué)森，陳樹友，許向東，儲昭坤

（1.合肥工業(yè)大學(xué)計算機(jī)與信息學(xué)院，安徽 合肥 230601；2.中國電信股份有限公司研究院，廣東 廣州 510630）

1 引言

根據(jù)思科2020年的統(tǒng)計[1]，視頻流量占據(jù)了整個網(wǎng)絡(luò)流量的 80%。在傳統(tǒng)網(wǎng)絡(luò)架構(gòu)中，用戶的訪問請求需要經(jīng)過基站的接入、核心網(wǎng)的訪問以及冗長的鏈路回傳才能完成，頻繁的用戶請求容易造成核心網(wǎng)絡(luò)的擁塞[2]。將熱點視頻在邊緣側(cè)進(jìn)行緩存，一方面可以減少縱向流量，另一方面還能降低時延，提升用戶體驗[3]。

其中，各類視頻門戶網(wǎng)站的電視劇播放量又占據(jù)了絕大部分的視頻流量，并且電視劇通常周期性地更新劇集。為了減少中心節(jié)點與邊緣節(jié)點內(nèi)容的反復(fù)遷移，將未來一個星期內(nèi)流行度較高的視頻放入緩存更有價值，因此對視頻流行度進(jìn)行準(zhǔn)確的中長期預(yù)測成為急需解決的問題[4]。

傳統(tǒng)的視頻流行度預(yù)測模型大致分為兩類：一類是以線性回歸與自回歸模型為代表的時間序列預(yù)測模型，參考文獻(xiàn)[5-7]基于歷史流行度構(gòu)建回歸預(yù)測模型，此類模型雖然訓(xùn)練簡單，但非線性映射能力差，很難捕捉流行度的動態(tài)變化，并且無法保留時間序列上的信息依賴，隨著時間步長的增加會逐漸失去對數(shù)據(jù)的學(xué)習(xí)能力，在中長期預(yù)測中表現(xiàn)不佳。另一類是基于特征提取與用戶聚類的有監(jiān)督學(xué)習(xí)方法來加強預(yù)測效果[8-9]，此類方法在一定程度上提高了模型的預(yù)測精度，但由于引入過多的外部變量，導(dǎo)致模型復(fù)雜度較高，極大地增加了模型的訓(xùn)練難度，不適用于實際應(yīng)用場景。隨著深度學(xué)習(xí)理論的不斷發(fā)展，具有較強學(xué)習(xí)能力的循環(huán)神經(jīng)網(wǎng)絡(luò)（recurrent neural network，RNN）和長短期記憶（long short-term memory，LSTM）網(wǎng)絡(luò)主要應(yīng)用于模式識別、語音處理等方面[10]，近年國內(nèi)外學(xué)者也將其應(yīng)用在船舶航跡、小區(qū)的負(fù)荷指標(biāo)等預(yù)測領(lǐng)域[11-12]，實驗表明預(yù)測精度優(yōu)于傳統(tǒng)方法，但是在視頻流行度預(yù)測領(lǐng)域的應(yīng)用有待進(jìn)一步研究。

基于以上分析，本文提出基于神經(jīng)網(wǎng)絡(luò)與馬爾可夫組合模型的視頻流行度預(yù)測算法，利用LSTM 結(jié)合雙向 RNN構(gòu)建雙向長短期記憶（bi-2irectional long short-term memory，BiLSTM）網(wǎng)絡(luò)模型，可以保留時間序列上兩個方向的特征依賴；并且考慮馬爾可夫具有根據(jù)系統(tǒng)當(dāng)前狀態(tài)對系統(tǒng)未來狀態(tài)進(jìn)行預(yù)測的性質(zhì)[13]，利用BiLSTM 網(wǎng)絡(luò)訓(xùn)練時產(chǎn)生的誤差信息建立馬爾可夫修正模型，在避免引入過多變量導(dǎo)致模型復(fù)雜度增加的情況下進(jìn)一步提高了網(wǎng)絡(luò)模型的預(yù)測精度。

2 基于神經(jīng)網(wǎng)絡(luò)與馬爾可夫的預(yù)測模型

2.1 BiLSTM網(wǎng)絡(luò)模型的構(gòu)建

回歸模型本質(zhì)上是對數(shù)據(jù)的線性擬合，不容易捕捉非線性的波動趨勢；傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)雖然可以有效地解決非線性映射問題，但在長時間序列訓(xùn)練過程中會出現(xiàn)梯度爆炸和梯度消失等問題。LSTM 通過引入控制門機(jī)制，可以在一定程度上避免此類問題，但LSTM的單向?qū)W習(xí)機(jī)制只能在一個方向上學(xué)習(xí)時間序列的數(shù)據(jù)特征。在視頻流行度的預(yù)測中，某個時間點視頻流行度的預(yù)測值，除了可由過去的數(shù)據(jù)進(jìn)行推導(dǎo)計算，未來時刻的數(shù)據(jù)也對當(dāng)前時刻流行度的計算有影響，因此本文在LSTM的基礎(chǔ)之上融入雙向RNN隱藏層構(gòu)建BiLSTM網(wǎng)絡(luò)模型。

BiLSTM網(wǎng)絡(luò)模型如圖1所示，BiLSTM通過神經(jīng)元之間的雙向隱藏層來保存兩個輸入方向的信息，可以有效學(xué)習(xí)流行度序列上兩個方向的關(guān)系依賴，增強了模型的學(xué)習(xí)能力；同時通過多層神經(jīng)網(wǎng)絡(luò)的疊加結(jié)構(gòu)實現(xiàn)了流行度序列深層次的特征挖掘，有效提高了模型的預(yù)測效果。

圖1 BiLSTM網(wǎng)絡(luò)模型

2.2 BiLSTM的馬爾可夫修正

為了進(jìn)一步提高模型的預(yù)測精度，如果通過繼續(xù)引入特征變量的方式，新的變量會作為輸入層的參數(shù)重新訓(xùn)練，過多的變量會導(dǎo)致模型訓(xùn)練困難。基于上述考慮，本文在不引入新的外部變量的情況下，通過對網(wǎng)絡(luò)模型的預(yù)測誤差建立馬爾可夫修正模型來進(jìn)一步提高模型的預(yù)測精度，如圖2所示。

圖2 馬爾可夫修正模型

其中，Pt+1為t+1時刻error狀態(tài)空間的概率分布，基于等距原則，進(jìn)而求得誤差修正值，如式（2）所示：

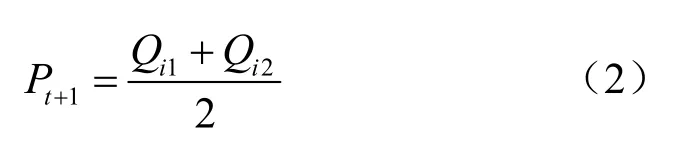
因此，本文視頻流行度的預(yù)測模型可以定義為式（3），其中pre2icti為網(wǎng)絡(luò)模型的預(yù)測值，mi22lei為求得的修正值，最終視頻流行度的求解可以轉(zhuǎn)化為Finali的求解：

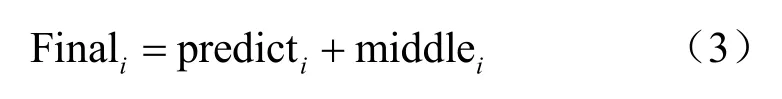
3 Mar-BiLSTM算法設(shè)計與求解

3.1 視頻流行度的預(yù)測問題描述

電視劇周期性地更新劇集，其中內(nèi)容熱度可以體現(xiàn)當(dāng)前劇集的受歡迎程度，用序列Popularity={popularity1,popularity2,… ,popularityn}描述電視劇當(dāng)前時刻的流行度。其中內(nèi)容熱度Popularity由平臺綜合播放量以及互動因子等指標(biāo)計算，更加能夠反映視頻的流行度。研究指出，電視劇的微博搜索指數(shù)和百度搜索指數(shù)與電視劇流行度具有很強的線性關(guān)系[14]，因此分別構(gòu)造微博指數(shù)序列 In 2ex1={in2ex11,in2ex12,…,in2ex1n}和百度搜索指數(shù)序列 I n2ex2={in2ex21, in2ex22,…,in2ex2n}；另外在新劇集更新當(dāng)天的電視劇播放量會比平常有一個明顯的增加，因此利用One-hot編碼構(gòu)造序列 F lag={+ l ag1, +lag2,… , + lagn}標(biāo)記該變化，其中+lag1代表星期一，+lag7代表星期日；最后利用預(yù)測模型φ預(yù)測下一個時間單位的電視劇流行度，如式（4）所示。

問題定義：在線電視劇T，已經(jīng)上線i天，流行度記為Popularity，特征序列為Feature，預(yù)測目標(biāo)為未來幾天流行度的記錄{popularityi+1,popularityi+2,… ,popularityi+n}。

3.2 Mar-BiLSTM流行度預(yù)測算法

基于第2.2節(jié)構(gòu)建的馬爾可夫修正的BiLSTM網(wǎng)絡(luò)模型，本文設(shè)計了Mar-BiLSTM算法來求解視頻流行度預(yù)測問題，算法框架如圖3所示。

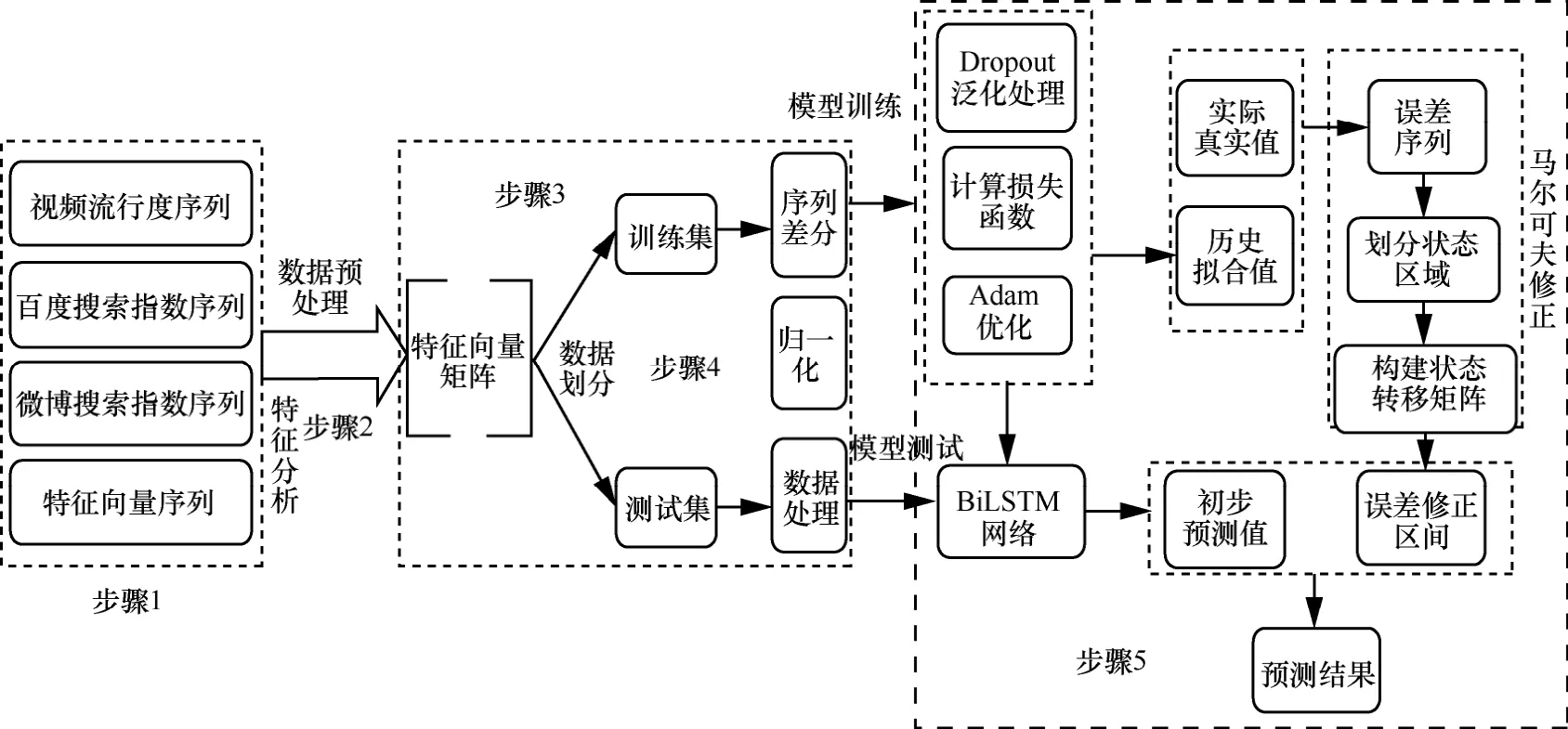
圖3 Mar-BiLSTM算法框架

Mar-BiLSTM算法大致可以分為5個步驟，算法的詳細(xì)流程如下。

步驟1基于Scrapy技術(shù)對電視劇的流行度進(jìn)行特征分析，得到In2ex1、 I n 2ex2、 F lag 等特征序列。

步驟 2獲取電視劇從上線開始后 3個星期的內(nèi)容熱度值popularityi，微博搜索指數(shù)值in2ex1i，百度搜索指數(shù)in2ex2i；+lagi表示當(dāng)天是否為劇集更新日，當(dāng)+lagi=1時表示當(dāng)天有劇集更新，+lagi=0 時表示當(dāng)天沒有劇集更新；進(jìn)而根據(jù)特征向量序列構(gòu)建特征向量矩陣。

步驟 3利用特征向量Feature進(jìn)行模型訓(xùn)練，取序列Popularity前兩個星期的數(shù)據(jù)作為模型的訓(xùn)練數(shù)據(jù)，最后一個星期的數(shù)據(jù)用于模型的檢驗；同時將序列處理為適合監(jiān)督學(xué)習(xí)的數(shù)據(jù)。

步驟 4對序列進(jìn)行差分處理，以此減小數(shù)據(jù)波動對模型訓(xùn)練的影響；同時采用min-max策略對原始數(shù)據(jù)進(jìn)行歸一化處理來消除量綱的差異，其轉(zhuǎn)換如式（5）所示：

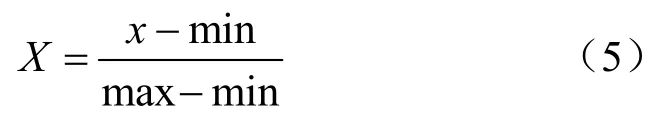
步驟 5采用自適應(yīng)估計方法計算每個參數(shù)的學(xué)習(xí)率；同時為避免過擬合現(xiàn)象采用 2ropout機(jī)制來提高模型的泛化能力；最后利用網(wǎng)絡(luò)模型的預(yù)測誤差建立馬爾可夫修正模型，根據(jù)式（3）得到修正后的流行度預(yù)測值Finali。

Mar-BiLSTM算法實現(xiàn)的偽代碼如算法1所示。

算法1Mar-BiLSTM算法

輸入訓(xùn)練集 Train_set，測試集 Test_set，屬性（特征序列）

輸出視頻流行度預(yù)測值

步驟1進(jìn)行特征分析，得到特征序列：

Popularity={popularity1,popularity2,…,popularityk},

k=1,2,…,21

In2ex1={in2ex11,in2ex12,…,in2ex1n},n=1,2,…,14

In2ex2={in2ex21,in2ex22,…,in2ex2m},1,2,…,14

Flag={+lag1, +lag2,…,+lags},s=1,2,… ，14

步驟2將各個時間序列進(jìn)行整合得到輸入時間序列：

concatSequence (i,i+ 1,…,t)

步驟3將時間序列數(shù)據(jù)轉(zhuǎn)化為有監(jiān)督數(shù)據(jù)：

I+I＞n_in an2I＜ 0

input sequence (t -n, …,t-1)

Else i+I＞ 0 an2I＜n_out

+orecast sequence (t,t+ 1, …,t+n)

步驟4max-min特征變換：

Return (Train_set)

Return (Test_set)

步驟5Train_set Train BiLSTM-Markov

Test_set Test BiLSTM-Markov

Return（均方根誤差、平均絕對誤差）

Return（流行度預(yù)測值）

en2

Mar-BiLSTM算法時間復(fù)雜度可分為5個部分。

步驟1時間復(fù)雜度可以記為O(|m|)；

步驟2序列整合的時間復(fù)雜度為O(|m|)；

步驟 3序列轉(zhuǎn)化為有監(jiān)督數(shù)據(jù)的時間復(fù)雜度為O(|n||m|)；

步驟 4max-min特征變換的時間復(fù)雜度為O(|n||m|)；

步驟 5計算均方根誤差及平均絕對誤差的時間復(fù)雜度為O(|n||m||i|)；因此，Mar-BiLSTM算法的時間復(fù)雜度為O(|n||m|)。

4 實驗設(shè)計與分析

4.1 實驗環(huán)境

實驗環(huán)境為聯(lián)想 Thinkpa2 E440筆記本計算機(jī)，CPU為Intel? CoreTM i5-4210 CPU @ 2.60 GHz，內(nèi)存為8 GB，操作系統(tǒng)為Bin2ows10教育版，使用基于Python3.5語言的PyCharm社區(qū)版集成開發(fā)工具構(gòu)建神經(jīng)網(wǎng)絡(luò)模型，利用MATLAB R2018b開發(fā)工具進(jìn)行對比試驗設(shè)計。

4.2 評價指標(biāo)

實驗采用預(yù)測模型常用的均方根誤差（root mean square2 error，RMSE）及平均絕對誤差（mean absolute error，MAE）作為預(yù)測性能的評價標(biāo)準(zhǔn)[15]。RMSE可以評價數(shù)據(jù)的變化情況，RMSE值越小，表示模型有更好的預(yù)測精確度，MAE可以更好地反映預(yù)測值與真實值偏離程度的實際情況，如式（6）、式（7）所示。

4.3 網(wǎng)絡(luò)模型參數(shù)選擇

隱藏層的層數(shù)以及神經(jīng)單元個數(shù)的選擇對網(wǎng)絡(luò)模型的性能影響很大，因此需要選擇訓(xùn)練誤差最小的網(wǎng)絡(luò)參數(shù)。不同W值下的RMSE值如圖4所示，在隱藏層數(shù)W=2、隱藏層單元個數(shù)L=6時的RMSE值最小，過多的隱藏層或者單元數(shù)都會使得網(wǎng)絡(luò)過于復(fù)雜而喪失網(wǎng)絡(luò)優(yōu)勢。因此，選擇W=2、L=6作為網(wǎng)絡(luò)模型的訓(xùn)練參數(shù)。

圖4 不同W值下的RMSE值

4.4 實驗設(shè)計及結(jié)果分析

實驗爬取電視劇《愛情公寓5》自2020年1月12日上線到同年2月1日的全網(wǎng)數(shù)據(jù)（其中包括播放量、評論數(shù)、點贊數(shù)、收藏數(shù)、百度搜索指數(shù)與微博搜索指數(shù)等），使用前兩個星期的數(shù)據(jù)訓(xùn)練模型、后一個星期的數(shù)據(jù)用來驗證本文算法的優(yōu)越性：首先選取回歸模型中常用于時間序列預(yù)測的灰色預(yù)測（grey mo2el，GM）與指數(shù)平滑（exponential smoothing，ES）驗證算法的有效性，進(jìn)而選取神經(jīng)網(wǎng)絡(luò)中常用于時間序列預(yù)測的傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)和 LSTM 神經(jīng)網(wǎng)絡(luò)驗證算法的優(yōu)越性；最后通過爬取2021年1月至2021年3月期間的10部首播電視劇的數(shù)據(jù)對其排名進(jìn)行預(yù)測，以此驗證算法的普適性。

4.4.1 LSTM與回歸模型對比

本節(jié)設(shè)計LSTM與GM、ES之間的對比實驗，以此來驗證 LSTM 的預(yù)測精度優(yōu)于傳統(tǒng)回歸模型。

GM、ES及LSTM模型的預(yù)測值對比如圖5所示，由于流行度數(shù)據(jù)不符合冪指數(shù)規(guī)律，因此基于指數(shù)規(guī)律建模的GM沒有很好地預(yù)測數(shù)據(jù)的波動規(guī)律；ES利用序列差分機(jī)制，可以預(yù)測很小的波動，但并不吻合真實數(shù)據(jù)的波動規(guī)律；LSTM基于 RNN與門控單元機(jī)制可以學(xué)習(xí)長時間序列上的信息依賴，對未來數(shù)據(jù)的波動給出了大致的

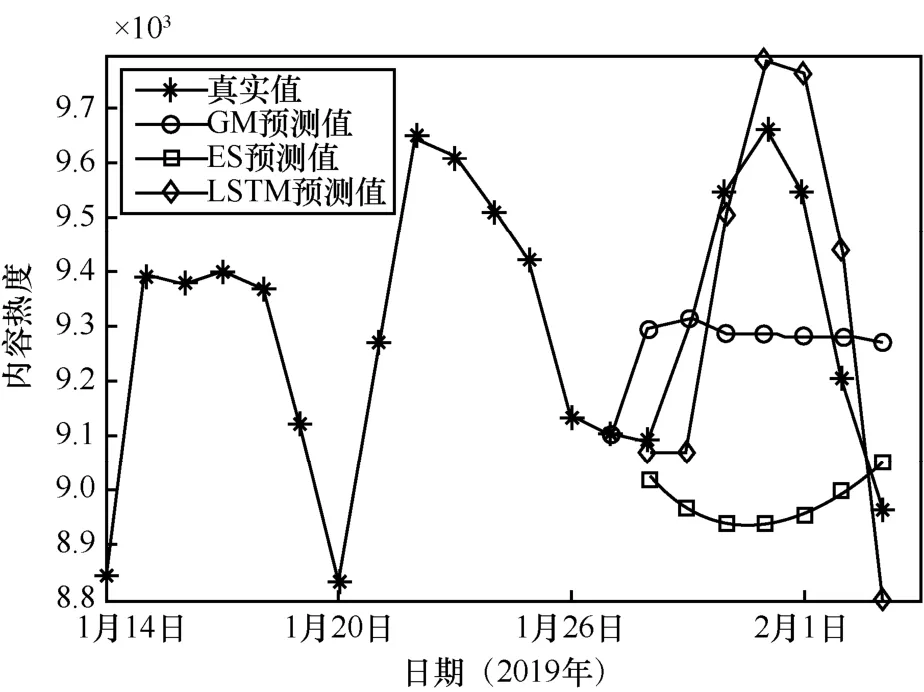
圖5 GM、ES及LSTM模型的預(yù)測值對比

預(yù)測，驗證了 LSTM 的預(yù)測效果優(yōu)于傳統(tǒng)回歸模型。

4.4.2 BiLSTM與BP、LSTM模型對比

本節(jié)設(shè)計了LSTM網(wǎng)絡(luò)與BP神經(jīng)網(wǎng)絡(luò)之間的對比試驗，就其預(yù)測精度及其收斂性進(jìn)行分析；在此基礎(chǔ)之上，引入BiLSTM進(jìn)行對比實驗，以此驗證BiLSTM的優(yōu)越性，為Mar-DBiLSTM組合預(yù)測理論模型提供實驗數(shù)據(jù)支撐。

BP、LSTM 模型訓(xùn)練誤差如圖6所示。BiLSTM、BP、及 LSTM 模型預(yù)測值對比如圖7所示。從圖6可以看出，LSTM較BP神經(jīng)網(wǎng)絡(luò)的收斂速度要快，在迭代次數(shù)為200次左右時，網(wǎng)絡(luò)已經(jīng)趨于收斂，此時BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練誤差還處于較高水平；同時從圖7可以看出，BP神經(jīng)網(wǎng)絡(luò)雖然能夠預(yù)測數(shù)據(jù)大致的波動趨勢，但 LSTM的預(yù)測曲線更加貼合于真實值，因此LSTM不僅學(xué)習(xí)性能強于傳統(tǒng)的神經(jīng)網(wǎng)絡(luò)，而且其預(yù)測效果也優(yōu)于普通的BP神經(jīng)網(wǎng)絡(luò)；基于LSTM改進(jìn)的BiLSTM 可以學(xué)習(xí)時間序列上兩個時間方向的信息依賴，因而能夠更好地對數(shù)據(jù)的波動趨勢進(jìn)行學(xué)習(xí)，從圖7也可以看出，BiLSTM較LSTM、BP均具有更高的預(yù)測精度，驗證了本文BiLSTM模型預(yù)測效果的優(yōu)越性。

圖6 BP、LSTM模型訓(xùn)練誤差

圖7 BiLSTM、BP及LSTM模型預(yù)測值對比

4.4.3 Mar-BiLSTM與BiLSTM模型對比

在前兩輪實驗的基礎(chǔ)之上，為了驗證Mar-BiLSTM 算法的有效性，設(shè)計該對比實驗。通過第2.2節(jié)的描述，對BiLSTM的預(yù)測誤差構(gòu)建馬爾可夫修正模型，最終可以求得未來幾天預(yù)測誤差可能的狀態(tài)區(qū)間，見表1。

表1 模型預(yù)測誤差狀態(tài)區(qū)間

由表1可知，26號最有可能的誤差狀態(tài)區(qū)間為 E3，由式（2）計算得到誤差修正值為 22，BiLSTM模型的預(yù)測值為9 096，根據(jù)式（3）得到修正后的預(yù)測值為9 091。在對27號誤差狀態(tài)進(jìn)行預(yù)測時，將26號誤差預(yù)測值作為已知值，并將最原始的信息剔除，按照上述方法重復(fù)，可以計算出接下來6天的誤差修正值。

由圖8可知，經(jīng)馬爾可夫修正過的BiLSTM預(yù)測值要更加貼近真實值，預(yù)測效果更好，證明了本文算法的優(yōu)越性。

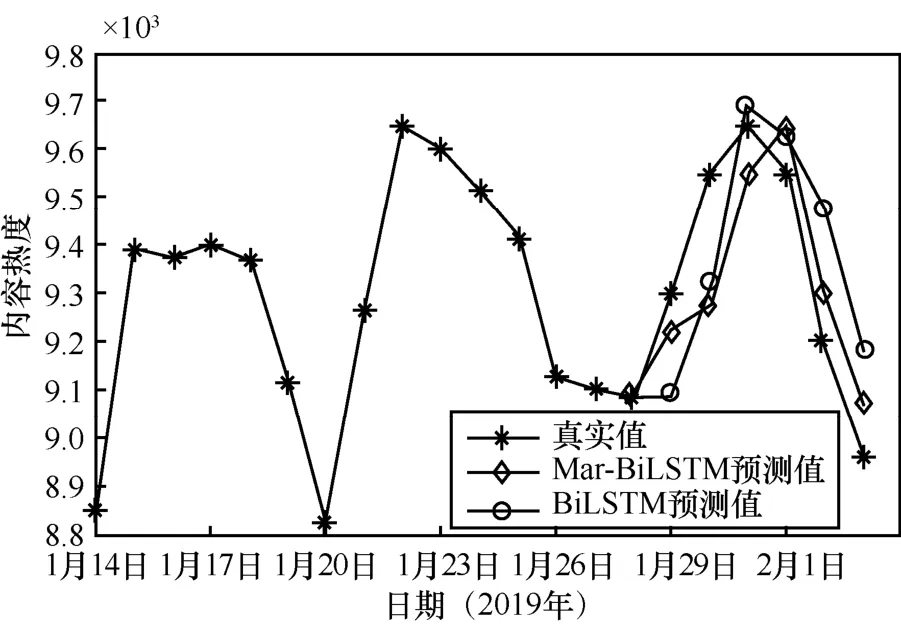
圖8 Mar-BiLSTM、BiLSTM模型預(yù)測值對比

綜上，根據(jù)第4.2節(jié)提出的性能指標(biāo)，給出對比預(yù)測模型的性能分析，見表2。

表2 性能對比

4.4.4 電視劇排名預(yù)測

為了進(jìn)一步驗證算法的普適性，從全網(wǎng)爬取2021年1月至3月期間首播的10部不同種類的電視劇數(shù)據(jù)，并對其排名進(jìn)行預(yù)測。由于電視劇并非在同一時間上線，其上線時間越長，累積播放量會越高；并且由于劇集數(shù)的不同，累計播放量也會有相應(yīng)的影響。因此，為了更加準(zhǔn)確地體現(xiàn)電視劇的真實排名，選擇均集播放量和均天播放量的加權(quán)值作為衡量電視劇真實排名的依據(jù)，排名預(yù)測結(jié)果見表3。

從表3可以看出，排名靠前的《斗羅大陸》《錦心似玉》《愛的理想生活》等熱播電視劇得到了準(zhǔn)確的預(yù)測，排名靠后的《你好，安怡》和《這個世界不看臉》等冷門電視劇也有較好的預(yù)測。因此，本文算法對不同類型電視劇的流行度均給出了不錯的預(yù)測效果，證明了算法的普適性較高。

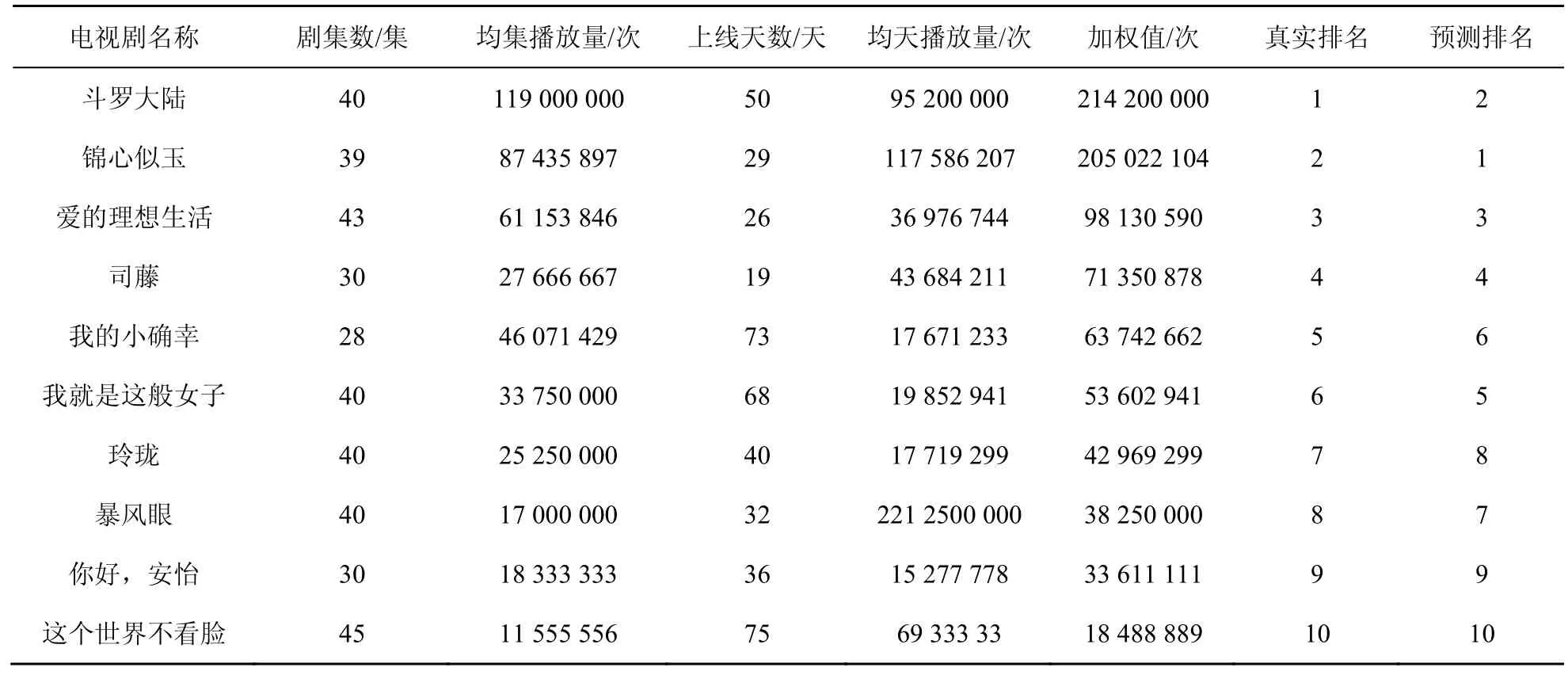
表3 電視劇排名預(yù)測結(jié)果

5 結(jié)束語

本文針對傳統(tǒng)視頻流行度預(yù)測算法非線性映射能力差，在中長期預(yù)測中存在精度低、自適應(yīng)性弱等缺點，提出基于神經(jīng)網(wǎng)絡(luò)與馬爾可夫組合模型的視頻流行度預(yù)測算法。該算法在預(yù)測過程中兼具時間相關(guān)性和非線性的特征，充分保留了時間序列上前向、后向兩個方向的長期依賴信息；并利用BiLSTM網(wǎng)絡(luò)訓(xùn)練時產(chǎn)生的預(yù)測誤差建立馬爾可夫修正模型，在避免引入過多變量導(dǎo)致模型復(fù)雜度增加的情況下進(jìn)一步提高了模型的預(yù)測精度。下一步工作擬將 Mar-BiLSTM 算法引入邊緣側(cè)的緩存調(diào)度策略中，嘗試建立根據(jù)視頻流行度預(yù)測的緩存替換策略，提高用戶的服務(wù)體驗質(zhì)量。