基于新型流形法的三維應(yīng)力強(qiáng)度因子求解

祁勇峰 蘇海東 龔亞琦

摘 要：為保證在裂紋尖端具有最佳的逼近，裂紋尖端的解析解與其周邊數(shù)值解聯(lián)合應(yīng)用的新型流形法可用來(lái)求解應(yīng)力強(qiáng)度因子，但僅限于平面問(wèn)題的Ⅰ型和Ⅱ型裂紋。沿用解析解與數(shù)值解聯(lián)合應(yīng)用的思路，以三維穿透直裂紋為研究對(duì)象，在裂紋尖端引入Williams解析解級(jí)數(shù)，應(yīng)用解析覆蓋與周邊數(shù)值覆蓋聯(lián)合求解三維應(yīng)力強(qiáng)度因子，相對(duì)于其他數(shù)值方法而言，計(jì)算精度高。推導(dǎo)相應(yīng)的剛度矩陣和應(yīng)變矩陣的表達(dá)式，通過(guò)典型算例驗(yàn)證了三維應(yīng)力強(qiáng)度因子精確求解方法的有效性。

關(guān)鍵詞：三維應(yīng)力強(qiáng)度因子;數(shù)值流形方法;裂紋尖端Williams解析級(jí)數(shù);解析覆蓋;數(shù)值覆蓋

Abstract： This paper proposes a new manifold method combined with the analytical solutions of the crack tip and its surrounding numerical solutions is used to solve the stress intensity factor to ensure the best approximation at the crack tip. But this method is limited to type I and type II cracks in the plane problem. This method follows the idea of combined application of analytical and numerical solutions. Taking the three-dimensional penetrating straight crack as the research object， the Williams analytical solution series is introduced at the crack tip， and the analytical covers and the surrounding numerical covers are combined to solve the 3D stress intensity factor. Compared with other numerical methods， this method has higher computational precision. Meanwhile， the corresponding formulas of the stiffness matrix and the strain matrix have been deduced，and typical numerical examples shows the validity of the method in solving the exact solution of the 3D stress intensity factor.

Keywords： 3D stress intensity factor; numerical manifold method; Williams series for crack tip; analytical covers; numerical covers

應(yīng)力強(qiáng)度因子準(zhǔn)則[1]是目前最常用的結(jié)構(gòu)裂縫擴(kuò)展準(zhǔn)則之一，基于線彈性斷裂力學(xué)的應(yīng)力強(qiáng)度因子（Stress Intensity Factor，簡(jiǎn)稱(chēng)SIF）是用來(lái)表征裂紋尖端附近應(yīng)力場(chǎng)和應(yīng)變場(chǎng)強(qiáng)度，是控制裂紋尖端應(yīng)力場(chǎng)和應(yīng)變場(chǎng)強(qiáng)度的關(guān)鍵參數(shù)，在裂紋擴(kuò)展分析中有著極其重要的地位。由于應(yīng)力強(qiáng)度因子取決于外力的大小和分布、結(jié)構(gòu)的幾何條件以及裂縫的形狀和位置，實(shí)際上只有少數(shù)問(wèn)題存在解析解，對(duì)于復(fù)雜幾何形狀和加載條件的問(wèn)題，只能通過(guò)數(shù)值方法來(lái)計(jì)算。目前裂縫擴(kuò)展分析的主流數(shù)值計(jì)算方法有有限元法、擴(kuò)展有限元法、數(shù)值流形法等。

有限元法[2-4]是目前分析裂縫等不連續(xù)問(wèn)題的主要方法，為體現(xiàn)裂紋尖端（下簡(jiǎn)稱(chēng)裂尖）周?chē)膽?yīng)力集中和奇異性，往往需要在裂尖附近的復(fù)雜應(yīng)力區(qū)布置高密度的單元網(wǎng)格，導(dǎo)致單元數(shù)目非常龐大;另外，在模擬裂縫擴(kuò)展過(guò)程時(shí)，需不斷重構(gòu)網(wǎng)格，因此，有限元法對(duì)網(wǎng)格的要求和依賴性極大地影響了計(jì)算效率。擴(kuò)展有限元法[5-7]通過(guò)在單元插值函數(shù)中引入能夠反映裂縫面特性的不連續(xù)階躍函數(shù)及反映裂尖局部特性的裂尖漸進(jìn)位移場(chǎng)函數(shù)，裂縫可以穿過(guò)單元內(nèi)部，裂縫擴(kuò)展以后無(wú)需重新劃分單元網(wǎng)格，采用同一網(wǎng)格就可以分析任意位置的裂縫問(wèn)題，克服了常規(guī)有限元進(jìn)行裂縫擴(kuò)展分析的缺點(diǎn)，極大地簡(jiǎn)化了前處理工作。數(shù)值流形方法[8-11]引入不連續(xù)覆蓋模擬裂縫，裂縫可以在網(wǎng)格內(nèi)部穿過(guò)，巧妙地解決了常規(guī)有限元法裂縫面必須與單元邊一致、裂縫擴(kuò)展后需要重新劃分網(wǎng)格的問(wèn)題。相對(duì)于擴(kuò)展有限元法設(shè)立不連續(xù)階躍函數(shù)的方式而言，這種方式效果更好，在裂縫非常靠近單元邊界時(shí)不會(huì)產(chǎn)生后者容易出現(xiàn)的數(shù)值誤差。但無(wú)論是常規(guī)有限元法在裂尖布置細(xì)密網(wǎng)格的方式，還是擴(kuò)展有限元法引入裂尖漸近位移場(chǎng)的方式，其主要目的都是為了提高裂尖附近的求解精度，從而提高應(yīng)力強(qiáng)度因子的計(jì)算精度，這些方法都有改進(jìn)的余地。即使是目前認(rèn)為最適合于裂縫擴(kuò)展分析的擴(kuò)展有限元法，由于其只是使用了裂尖漸近位移場(chǎng)的部分特征函數(shù)，嚴(yán)格地說(shuō)，還不能構(gòu)成對(duì)裂尖位移場(chǎng)的最佳逼近。文獻(xiàn)[12]提出的新型數(shù)值流形方法，實(shí)現(xiàn)了裂紋尖端的解析解與其周邊數(shù)值解聯(lián)合應(yīng)用以求解應(yīng)力強(qiáng)度因子，能夠采用裂尖真實(shí)位移場(chǎng)的最佳逼近，并直接得到應(yīng)力強(qiáng)度因子，計(jì)算精度高，但僅限于平面問(wèn)題的Ⅰ型和Ⅱ型裂紋。

在上述研究的基礎(chǔ)上，沿用解析解與數(shù)值解聯(lián)合應(yīng)用的思路，在裂紋尖端直接引入Williams解析解作為數(shù)學(xué)覆蓋，應(yīng)用裂紋尖端的解析解與周邊數(shù)值解的三維流形覆蓋聯(lián)系技術(shù)，可直接得出裂紋尖端的三維應(yīng)力強(qiáng)度因子，精度高且計(jì)算收斂快。

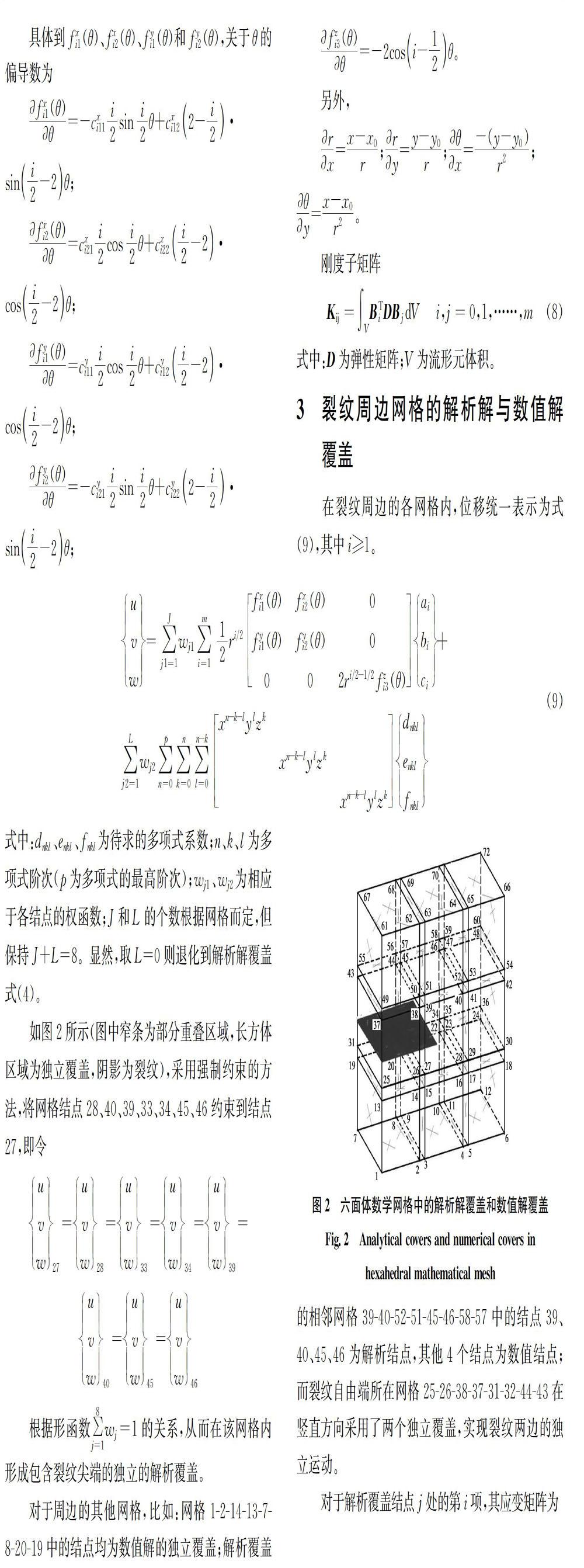
隨著覆蓋函數(shù)階數(shù)的增加，三維應(yīng)力強(qiáng)度因子計(jì)算值基本接近理論值。Williams級(jí)數(shù)的階數(shù)以及周邊數(shù)值覆蓋階數(shù)對(duì)計(jì)算值有較大影響。

1）Williams級(jí)數(shù)的階數(shù)（m）影響最大。當(dāng)m≤3，則KI與理論值相差較大;當(dāng)m≥4時(shí)，KI接近理論值。

2）周邊數(shù)值覆蓋階數(shù)升高有利于提高解的精度。當(dāng)周邊數(shù)值解取1階時(shí)，KI的計(jì)算值普遍小于取2階的情況，當(dāng)m≥4時(shí)，KI與理論值接近，但仍有差距，僅當(dāng)m取為7時(shí)才達(dá)到1.42，與理論值1.45最為接近。而當(dāng)周邊數(shù)值覆蓋取2階，m≥7時(shí)，計(jì)算值與理論值基本一致。

前期平面問(wèn)題研究表明，在大的覆蓋中單純依靠提高覆蓋函數(shù)階次的方法往往會(huì)帶來(lái)計(jì)算結(jié)果的振蕩跳躍。反之，如果采用較小的覆蓋而用相對(duì)簡(jiǎn)單的低階多項(xiàng)式，則可以更好地逼近實(shí)際復(fù)雜的分布情況。表2的計(jì)算結(jié)果也說(shuō)明，三維問(wèn)題中，基于大覆蓋，僅僅采用提高級(jí)數(shù)解及相鄰覆蓋函數(shù)的階數(shù)的做法來(lái)提高計(jì)算精度，計(jì)算也表現(xiàn)出一定的不穩(wěn)定性，要取得滿意的計(jì)算精度，裂紋尖端及其周邊的覆蓋函數(shù)的階數(shù)不小于7階。

考慮到裂紋所在的獨(dú)立覆蓋區(qū)域較大，因此，將裂紋所在的獨(dú)立覆蓋進(jìn)行局部加密，將裂紋尖端覆蓋分別加密1倍及2倍，采用局部覆蓋加密技術(shù)[16]，重新計(jì)算應(yīng)力強(qiáng)度因子，如表2所示。

表2結(jié)果表明，當(dāng)裂紋尖端獨(dú)立覆蓋加密1倍后、Williams級(jí)數(shù)的階數(shù)≥4或當(dāng)裂紋尖端獨(dú)立覆蓋加密2倍后，Williams級(jí)數(shù)的階數(shù)≥3時(shí)，KI與理論解十分接近，且隨著Williams級(jí)數(shù)階數(shù)的提高，計(jì)算結(jié)果趨于穩(wěn)定。

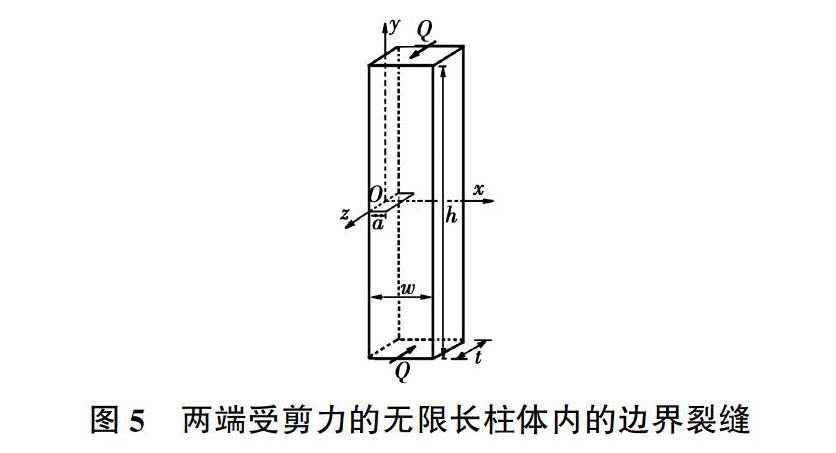
4.2 兩端受剪切荷載作用

考慮三維荷載作用下的算例。如圖5所示，無(wú)限長(zhǎng)柱沿z方向施加均布荷載Q=100 kN/m2，裂紋長(zhǎng)度a=0.02 m，柱體尺寸以及材料參數(shù)同上，其應(yīng)力強(qiáng)度因子理論值為KIII=Qπc[15]，其中c=aw。KIII的理論值為2.51。

流形元網(wǎng)格如圖6所示，共劃分18個(gè)獨(dú)立覆蓋（方塊區(qū)域）和25個(gè)部分重疊覆蓋（窄條區(qū)域），每個(gè)獨(dú)立覆蓋的大小基本相同。裂紋所在的獨(dú)立覆蓋區(qū)域大小為0.2 m×0.2 m×1 m（長(zhǎng)×寬×厚），柱體底面施加法向約束。應(yīng)力強(qiáng)度因子的計(jì)算結(jié)果見(jiàn)表3。

表3計(jì)算結(jié)果表明：采用圖6所示計(jì)算網(wǎng)格，當(dāng)m≥7時(shí)，周邊數(shù)值覆蓋階數(shù)取2、3的多項(xiàng)式階數(shù)時(shí)，計(jì)算結(jié)果與理論值比較符合。當(dāng)m≤7，計(jì)算結(jié)果與理論值有一定差別，局部數(shù)值出現(xiàn)跳躍，表明裂紋附近的網(wǎng)格還沒(méi)有達(dá)到足夠的密度。當(dāng)網(wǎng)格加密一倍后，周邊數(shù)值覆蓋階數(shù)均取2階，當(dāng)m≥7時(shí)，計(jì)算值與理論值十分接近，且隨著階數(shù)的提高，計(jì)算結(jié)果趨于穩(wěn)定。

以上算例驗(yàn)證了三維裂縫計(jì)算公式和程序的正確性，表明裂紋尖端解析解覆蓋和周邊數(shù)值解覆蓋聯(lián)合應(yīng)用求解三維線彈性斷裂力學(xué)問(wèn)題可行。與常規(guī)有限元方法相比，無(wú)需在裂紋尖端布置細(xì)密的網(wǎng)格，計(jì)算精度高，收斂相對(duì)較快。

裂紋尖端獨(dú)立覆蓋的密度、解析覆蓋的級(jí)數(shù)以及相鄰數(shù)值覆蓋的階數(shù)是影響應(yīng)力強(qiáng)度因子計(jì)算精度的重要因素，但在保證獨(dú)立覆蓋有一定密度的情況下，提高與獨(dú)立覆蓋相鄰數(shù)值覆蓋的階數(shù)可以得到應(yīng)力強(qiáng)度因子的精確解。

裂紋尖端獨(dú)立覆蓋的合理布置對(duì)應(yīng)力強(qiáng)度因子的計(jì)算精度及穩(wěn)定性有一定的影響，因此，下一步要重點(diǎn)研究裂紋尖端附近的覆蓋自動(dòng)布置及密度問(wèn)題，以保證方法的收斂性，便于開(kāi)展三維裂縫擴(kuò)展的動(dòng)態(tài)模擬研究。

5 結(jié)論

將裂紋尖端解析解覆蓋和周邊數(shù)值解覆蓋聯(lián)合應(yīng)用，分析三維線彈性斷裂力學(xué)問(wèn)題，得到以下主要結(jié)論：

1）在包含裂紋尖端的解析覆蓋中，應(yīng)用裂紋尖端附近的Williams位移解析解作為覆蓋函數(shù)，并采用高階多項(xiàng)式三維覆蓋函數(shù)與解析覆蓋的條形連接技術(shù)，實(shí)現(xiàn)了在解析覆蓋中直接求得裂紋尖端的三維應(yīng)力強(qiáng)度因子。

2）典型的張開(kāi)型和撕開(kāi)型的裂紋算例表明，應(yīng)力強(qiáng)度因子的計(jì)算精度較高。鑒于三維裂縫擴(kuò)展問(wèn)題的復(fù)雜性，裂紋尖端周邊數(shù)值覆蓋階數(shù)以及獨(dú)立覆蓋網(wǎng)格密度對(duì)應(yīng)力強(qiáng)度因子計(jì)算精度的影響較二維問(wèn)題更大。因此，協(xié)調(diào)獨(dú)立覆蓋密度、階數(shù)與周邊三維數(shù)值覆蓋階數(shù)的關(guān)系，來(lái)保證高精度求解收斂性的快速、穩(wěn)定是下一步研究的重點(diǎn)。

考慮到解析級(jí)數(shù)是裂尖附近真實(shí)位移場(chǎng)的最佳逼近，相比其他方法而言，可以認(rèn)為該方法在應(yīng)力強(qiáng)度因子求解方面逼近效果更好、收斂更快，同時(shí)，由于網(wǎng)格布置根據(jù)不同區(qū)域的精度要求，只在裂尖附近進(jìn)行覆蓋加密，因此，相比采用均勻網(wǎng)格的擴(kuò)展有限元而言，計(jì)算效率將有所提高，可以實(shí)現(xiàn)大規(guī)模計(jì)算。另外，應(yīng)力強(qiáng)度因子SIF本身就是裂尖解析級(jí)數(shù)的未知數(shù)，在求解系統(tǒng)方程組時(shí)一并得到，而不需要像其它方法那樣通過(guò)所謂的“直接”法或“間接”法來(lái)推求，不僅方便，而且不會(huì)引入額外誤差，這也是該方法的優(yōu)勢(shì)所在。

該方法可以同時(shí)求解Ⅰ型、Ⅱ型、Ⅲ型（撕開(kāi)型）裂紋的應(yīng)力強(qiáng)度因子，應(yīng)用復(fù)合型裂紋擴(kuò)展準(zhǔn)則就可以判斷其是否繼續(xù)開(kāi)裂，因此，該方法在三維裂縫擴(kuò)展的動(dòng)態(tài)模擬方面極具應(yīng)用前景。

參考文獻(xiàn)：

[1] PEREZ N. Linear-elastic fracture mechanics [M]∥ Fracture Mechanics. Cham： Springer International Publishing， 2016： 79-130.

[2] FAGEEHI Y A， ALSHOAIBI A M. Nonplanar crack growth simulation of multiple cracks using finite element method [J]. Advances in Materials Science and Engineering， 2020， 2020： 1-12.

[3] ALSHOAIBI M. Finite element simulation of crack growth path and stress intensity factors evaluation in linear elastic materials [J]. Jounal of Computational and Applied Research in Mechanical Engineering， 2019.

[4] HAJIAN M， MORADI M. An improved approach for computation of stress intensity factors using the finite element method [J]. Engineering Analysis with Boundary Elements， 2019（1）： 54-63.

[5] 李錄賢， 王鐵軍. 擴(kuò)展有限元法（XFEM）及其應(yīng)用[J]. 力學(xué)進(jìn)展， 2005， 35（1）： 5-20.

LI L X， WANG T J. The extended finite element method and its applications： A review [J]. Advances in Mechanics， 2005， 35（1）： 5-20. （in Chinese）

[6] GINER E， SUKUMAR N， DENIA F D， et al. Extended finite element method for fretting fatigue crack propagation [J]. International Journal of Solids and Structures， 2008， 45（22/23）： 5675-5687.

[7] ELGUEDJ T， DE SAINT MAURICE R P， COMBESCURE A， et al. Extended finite element modeling of 3D dynamic crack growth under impact loading [J]. Finite Elements in Analysis and Design， 2018， 151： 1-17.

[8] 石根華. 數(shù)值流形方法與非連續(xù)變形分析[M]. 裴覺(jué)民， 譯. 北京： 清華大學(xué)出版社， 1997.

SHI G H.Numerical manifold method and discontinuous deformation analysis [M]. PEI J M， translated. Beijing： Tsinghua University Press， 1997.

[9] YANG S K， CAO M S， REN X H， et al. 3D crack propagation by the numerical manifold method [J]. Computers & Structures， 2018， 194： 116-129.

[10] ZHANG G X， LI X， LI H F. Simulation of hydraulic fracture utilizing numerical manifold method [J]. Science China Technological Sciences， 2015， 58（9）： 1542-1557.

[11] ZHENG H， LIU F， DU X L. Complementarity problem arising from static growth of multiple cracks and MLS-based numerical manifold method [J]. Computer Methods in Applied Mechanics and Engineering， 2015， 295： 150-171.

[12] 蘇海東， 祁勇峰， 龔亞琦. 裂紋尖端解析解與周邊數(shù)值解聯(lián)合求解應(yīng)力強(qiáng)度因子[J]. 長(zhǎng)江科學(xué)院院報(bào)， 2013， 30（6）： 83-89.

SU H D， QI Y F， GONG Y Q. Compute stress intensity factors via combining analytical solutions around crack tips with surrounding numerical solutions [J]. Journal of Yangtze River Scientific Research Institute， 2013， 30（6）： 83-89.（in Chinese）

[13] 祁勇峰， 蘇海東， 崔建華. 部分重疊覆蓋的數(shù)值流形方法初步研究[J]. 長(zhǎng)江科學(xué)院院報(bào)， 2013， 30（1）： 65-70.

QI Y F， SU H D， CUI J H. Preliminary study on numerical manifold method with partially overlapping covers [J]. Journal of Yangtze River Scientific Research Institute， 2013， 30（1）： 65-70. （in Chinese）

[14] 王勖成. 有限單元法[M]. 北京： 清華大學(xué)出版社， 2003.

WANG X C. Finite element method [M]. Beijing： Tsinghua University Press， 2003.（in Chinese）

[15] 中國(guó)航空研究院. 應(yīng)力強(qiáng)度因子手冊(cè) [M]. 北京： 科學(xué)出版社， 1993.

Chinese Aeronautical Establishment. Stress intensity factors handbook [M]. Beijing： Science Press， 1993.（in Chinese）

[16] 蘇海東， 龔亞琦， 頡志強(qiáng)， 等. 基于矩形獨(dú)立覆蓋初步實(shí)現(xiàn)結(jié)構(gòu)靜力分析的自動(dòng)計(jì)算[J]. 長(zhǎng)江科學(xué)院院報(bào)， 2016， 33（2）： 144-150.

SU H D， GONG Y Q， XIE Z Q， et al. Preliminary implementation of automatic computation for static analysis of structures using NMM based on independent rectangular covers [J]. Journal of Yangtze River Scientific Research Institute， 2016， 33（2）： 144-150. （in Chinese）

（編輯 章潤(rùn)紅）