跨座式單軌列車-軌道梁耦合動(dòng)力學(xué)特性研究

馬濕洪

摘要：跨座式單軌列車-軌道梁系統(tǒng)的耦合振動(dòng)問題涉及因素多，有待進(jìn)一步研究。基于剛?cè)狁詈侠碚摻⒖缱絾诬壛熊?軌道梁耦合動(dòng)力學(xué)模型，以探討不同軌道梁跨距和載重狀態(tài)對(duì)系統(tǒng)響應(yīng)的影響。結(jié)果表明：軌道梁跨中豎向撓度和橫向撓度均隨跨距的增加而增大，跨中豎向撓度影響更顯著;跨中豎向撓度隨載客量的增大而增大，橫向撓度基本不受載客量的影響。研究可為跨座式單軌交通系統(tǒng)的結(jié)構(gòu)設(shè)計(jì)優(yōu)化和運(yùn)輸管理提供理論基礎(chǔ)。

關(guān)鍵詞：跨座式單軌;列車-軌道梁耦合;跨距;載重;運(yùn)行平穩(wěn)性

中圖分類號(hào)：U441? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻(xiàn)標(biāo)識(shí)碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號(hào)：1674-957X（2021）05-0040-02

0? 引言

列車和軌道梁結(jié)構(gòu)之間形成了一個(gè)相互作用、相互影響的多自由度振動(dòng)系統(tǒng)，但目前針對(duì)跨座式單軌-軌道梁耦合動(dòng)力學(xué)模型及特性的研究仍然匱乏。KenjiroGoda[1]教授建立三自由度跨座式單軌車輛-軌道動(dòng)力模型，對(duì)單軌車輛曲線通過性能進(jìn)行仿真，結(jié)果表明機(jī)車車輛轉(zhuǎn)向架導(dǎo)向輪徑向力大于拖車車輛轉(zhuǎn)向架導(dǎo)向輪徑向力。C.H.Lee等[2]建立了15自由度車輛模型，并采用模特疊加法建立了橋梁分析模型，以研究車速、旅客數(shù)量等因素對(duì)旅客舒適性的影響。并在另一研究中提出了軌道梁的橫向位移來源于橋梁剪心與列車豎向荷載偏心引起的扭轉(zhuǎn)效應(yīng)[3]。

基于以上研究，本文分析了跨座式單軌車輛一軌道梁動(dòng)力相互作用機(jī)理，基于剛-柔耦合理論，建立跨座式單軌列車-軌道梁空間耦合動(dòng)力學(xué)分析模型。探討了不同軌道梁跨距和載重狀態(tài)對(duì)耦合系統(tǒng)振動(dòng)響應(yīng)的影響水平。

1? 跨座式單軌列車-軌道梁耦合動(dòng)力學(xué)模型

1.1 跨座式單軌車輛動(dòng)力學(xué)子模型

對(duì)于單節(jié)單軌車輛，通常將車體、前后轉(zhuǎn)向架視為剛體，忽略其彈性變形影響，其中車體和轉(zhuǎn)向架相對(duì)于總體慣性坐標(biāo)系都具有2個(gè)平動(dòng)和3個(gè)轉(zhuǎn)動(dòng)自由度，分別為橫移（y）、沉浮（z）、側(cè)滾（φ）、搖頭（ψ）和點(diǎn)頭（θ）運(yùn)動(dòng)，共15個(gè)自由度。基于拉格朗日方程對(duì)15自由度車輛模型進(jìn)行建立：

1.1.1 車體橫移、沉浮方程

???? （1）

（2）

1.1.2 前、后轉(zhuǎn)向架橫移、沉浮方程

（3）

1.2 軌道梁振動(dòng)模型

本文基于有限元法建立軌道梁空間振動(dòng)模型，均采用空間離散梁?jiǎn)卧總€(gè)節(jié)點(diǎn)有6個(gè)自由度。其基本思路是，首先將復(fù)雜的軌道梁結(jié)構(gòu)離散成有限個(gè)單元的集合體，然后在各自單元內(nèi)選擇合適的位移模式，并計(jì)算每個(gè)單元及整個(gè)軌道梁結(jié)構(gòu)的動(dòng)能和應(yīng)變能，再由Hamilton原理推導(dǎo)出軌道梁結(jié)構(gòu)振動(dòng)無阻尼微分方程，最后采用Craig-Bampton固定界面模態(tài)綜合法進(jìn)行軌道梁結(jié)構(gòu)振動(dòng)響應(yīng)的求解。因此，軌道梁有限元模型的無阻尼運(yùn)動(dòng)方程可表示為：

（4）

式中：Mb、Kb分別為質(zhì)量、剛度矩陣;ub為節(jié)點(diǎn)位移向量;Fb為荷載列向量。

基于Craig-Bampton法，將子結(jié)構(gòu)的位移劃分為結(jié)構(gòu)內(nèi)部節(jié)點(diǎn)位移ui和界面節(jié)點(diǎn)位移uj，故式（5）無阻尼運(yùn)動(dòng)微分方程可改寫為分塊矩陣形式：

（5）

式中：F內(nèi)部節(jié)點(diǎn)處內(nèi)力矩陣;F為界面處的內(nèi)力矩陣。

式（6）經(jīng)過坐標(biāo)轉(zhuǎn)換，以振型疊加項(xiàng)來替代位移矢量，經(jīng)過方程簡(jiǎn)化可得到運(yùn)動(dòng)方程的簡(jiǎn)化形式為：

（6）

引入模態(tài)矩陣φb和模態(tài)坐標(biāo)qb，其節(jié)點(diǎn)位移可表示為：

（7）

式中：φm為主模態(tài)矩陣;φn為約束模態(tài)矩陣;qb為提取的模態(tài)數(shù)。

1.3 輪胎模型

本文選擇基于彈性地基梁理論的FIALA輪胎模型來描述走行輪、導(dǎo)向輪、穩(wěn)定輪的力學(xué)行為。根據(jù)FIALA輪胎模型，輪胎側(cè)向力方程可以表示為如下：

當(dāng)時(shí)：

（8）

當(dāng)時(shí)：

（9）

式中：θ是側(cè)偏角;Cy為側(cè)偏剛度;sy側(cè)向滑移率。

2? 跨座式單軌列車-軌道梁耦合系統(tǒng)動(dòng)力學(xué)響應(yīng)

2.1 曲線半徑對(duì)軌道梁系統(tǒng)動(dòng)態(tài)響應(yīng)的影響

分析曲線半徑在100～1000m范圍內(nèi)變化時(shí)對(duì)跨座式單軌車橋耦合系統(tǒng)振動(dòng)響應(yīng)的影響，仿真取車速40km/h，圖1為軌道梁跨中豎、橫撓度隨曲率半徑的變化曲線，由圖1可知，軌道梁的垂向撓度隨曲率半徑的增加而減小，曲率半徑為100m時(shí)其峰值為10.6mm，而橫向撓度隨曲率半徑的增加而增加。

2.2 跨徑和載重對(duì)軌道梁系統(tǒng)動(dòng)態(tài)響應(yīng)的影響

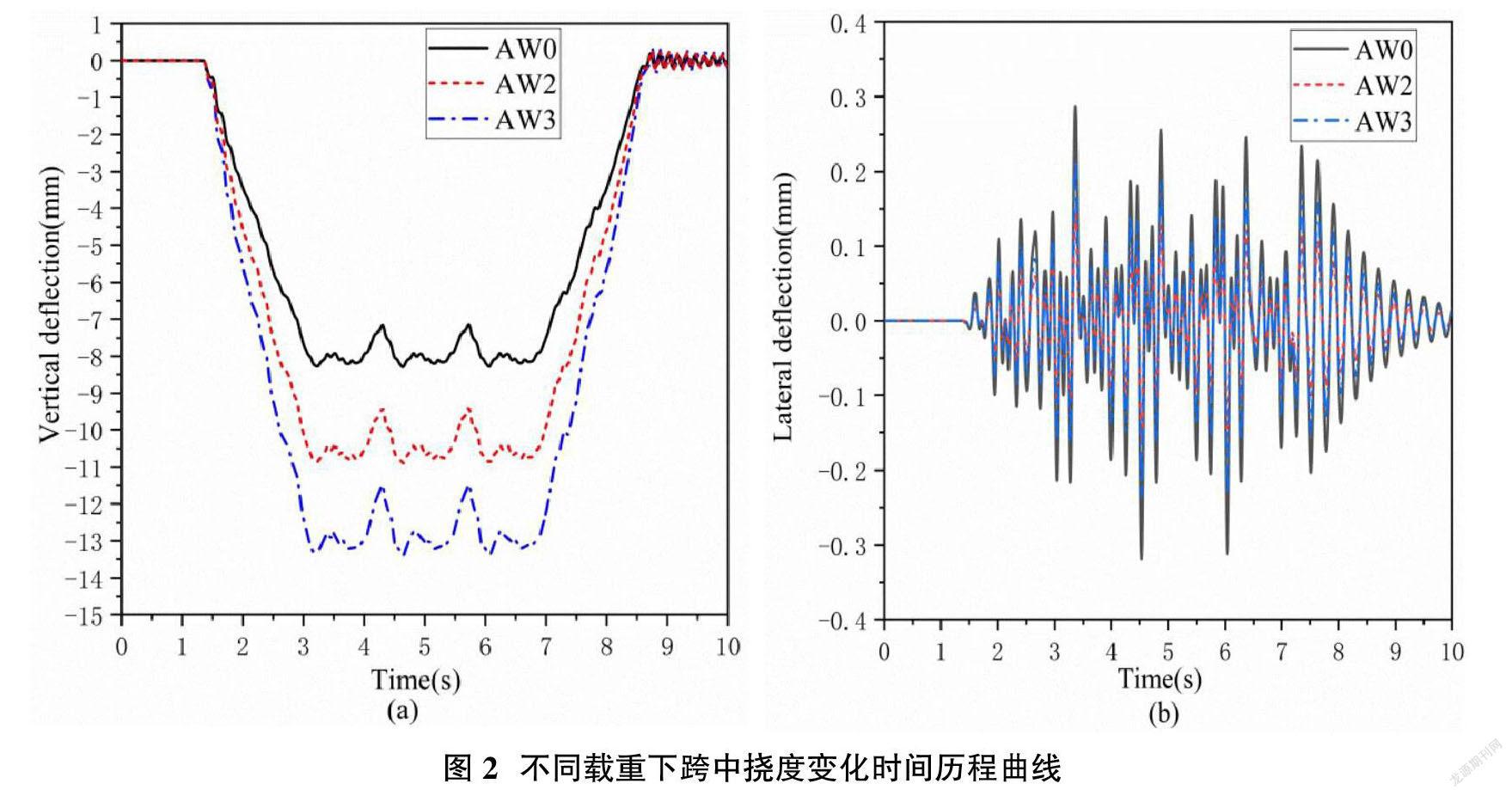
跨座式單軌交通軌道梁常見跨度一般在10-25m之間變化。因而，參數(shù)敏感性分析中，橋梁的跨度從10m逐漸增加到25m，考慮三種車輛荷載（空車（AW0）、定員（AW2）和滿載（AW3））對(duì)軌道梁動(dòng)態(tài)響應(yīng)的影響。

圖2為不同載荷下軌道梁跨中撓度時(shí)間歷程曲線，由圖2可知，隨著載荷的增加，橫豎向撓度均增大，車輛滿載時(shí)，豎向和橫向的最大撓度分別為13.2mm和0.32mm，車輛荷載對(duì)軌道梁有顯著影響，跨距大于20m后急劇增加，軌道梁跨中橫向撓度變化較為平緩;表明車輛超員狀態(tài)為控制軌道梁豎向抗彎剛度設(shè)計(jì)的最不利狀態(tài)。

3? 結(jié)論

通過本文建立的跨座式單軌列車-軌道梁耦合動(dòng)力學(xué)模型，研究不同軌道梁跨距和載客量工況對(duì)車輛系統(tǒng)響應(yīng)的影響，結(jié)果表明：軌道梁跨中豎向位移和橫向位移均隨跨距的增加而增加，且跨中豎向位移變化幅度較大;跨中豎向位移隨載客量的增大而增大，橫向位移基本不受載重的影響。軌道梁的豎向加速度隨跨徑的增加先增后減，在跨距為18m左右出現(xiàn)拐點(diǎn)，峰值為0.84m/s2。

參考文獻(xiàn)：

[1]GodaK， Nishigaito T， Hiraishi M， et al. A curving simulation for a monorail car[C]. Railroad Conference， 2000. Proceedings of the 2000 ASME/IEEE Joint. IEEE， 2000.

[2]Lee Chang Hun， Kim ChulWoo， KawataniM， et al. Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains[J]. Engineering Structures， 2005， 27（14）： 1999-2013.

[3]C H. Lee， et al. Dynamic response of a monorail steel bridge under a moving train UJ]， Journal ofsound & Vibration 294（2006）， 562-579.

[4]Craig R. R. Jr. Bampton M. C.C. Coupling of Substructures for Dynamics Analyses]. ALAAJournal. 1968， 6（7）： 1313-1319.