錯聯齒輪傳動應力及嚙合剛度分析

張建文 葉友東 蔡志盛

摘要：為了對比普通齒輪傳動和錯聯齒輪傳動中應力和嚙合剛度的不同，在 Solidworks 中，建立了直齒和錯聯圓柱齒輪傳動模型，將模型導入 workbench的瞬態動力學模塊進行有限元分析。結果表明錯聯齒輪比普通齒輪在傳動時的嚙合剛度大、承載能力強;錯開1/2齒距比錯開1/3齒距錯聯齒輪傳動嚙合剛度更大、應力應變更小的特點。

關鍵詞：錯聯齒輪傳動;嚙合剛度;有限元分析

中圖分類號：TH132.4? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1674-957X（2021）15-0051-02

0? 引言

齒輪是機械動力傳動中應用最廣的一種傳動零件，它具有結構緊湊、傳遞動力大、機械效率高、使用壽命長、工作可靠性好和傳動比準確等優點。何育民[1]等通過使用三維建模軟件 Solidworks 分析齒輪在仿真中嚙合剛度的時變性問題。Zhan 等[2]利用有限元軟件 workbench 用準靜態方法求解了嚙合剛度，并研究了齒頂圓角及主從動輪軸不平行時對嚙合剛度的影響。趙慶彬[3]等分析了面齒輪傳動嚙合剛度問題，驗證了理論方法的可靠性，卜忠紅[4]運用線性規劃法分析了斜齒輪副的時變嚙合剛度，闡述了其變動原理。

本文提出了由兩個錯聯齒輪相互嚙合組成的一種新型的齒輪傳動裝置，如圖1所示。齒輪1和齒輪1’的參數完全相同，并且兩個齒輪彼此沿圓周方向依次錯開一定的齒距，如錯開1/2和1/3齒距等;齒輪2和齒輪2’的參數完全相同，兩個齒輪彼此沿圓周方向依次錯開與齒輪1相同的齒距，使得兩個錯聯齒輪相嚙合。

1? 錯聯齒輪傳動模型的建立及有限元設置

錯聯齒輪及普通圓柱齒輪建模的參數為齒輪的齒輪1、1’齒數為30，齒寬為30mm;齒輪2、2’齒數為50，齒寬為30mm;齒輪的齒輪3齒數為30，齒寬為60mm;齒輪的齒輪4齒數為50，齒寬為60mm。齒輪的模數均為4，壓力角均為為20°，材料為均為45號鋼。圖1為錯聯齒輪傳動模型。

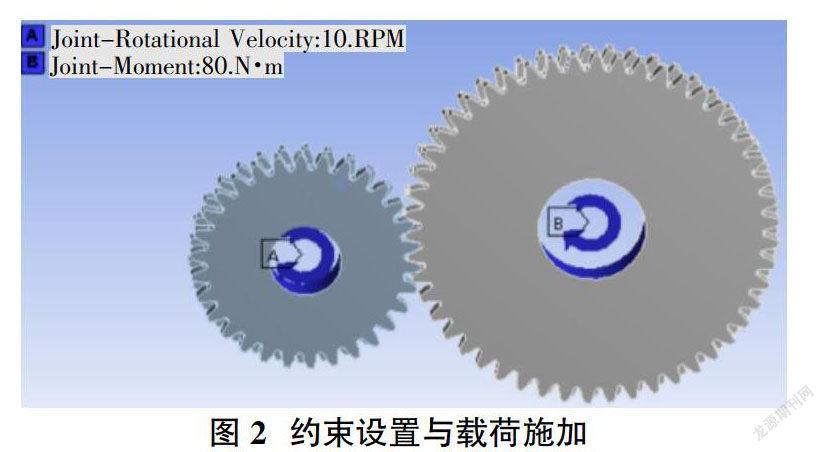
將齒輪傳動裝配體模型通過Solidworks與ANSYS workbench的接口直接導入ANSYS workbench的瞬態動力學模塊，并且兩次分析使用相同的條件[5]。由于每對輪齒嚙合圖2是主從動輪施加邊界條件的過程，左邊是主動輪，右邊為從動輪，主從動輪軸孔處添加旋轉副約束。主動輪旋轉副施加10r/min恒定轉速，從動輪旋轉副施加80N·m轉矩，之后進行網格劃分和仿真分析[6]。

2? 應力分析

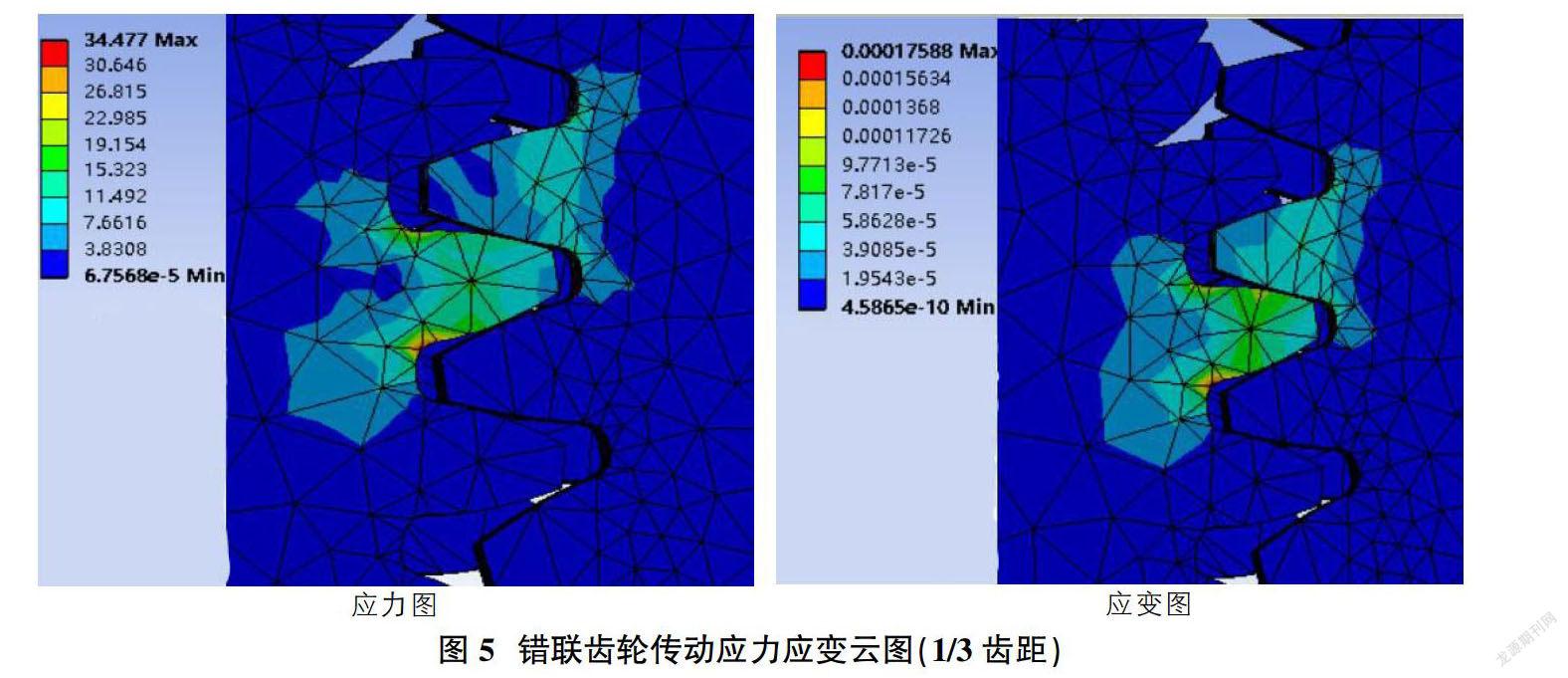
通過有限元分析可以得到齒輪嚙合的表面接觸應力和應變分布云圖，如圖3、圖4和圖5所示，直觀地反映了接觸應力的分布。從齒輪傳動應力云圖和應變云圖可知，錯聯齒輪傳動與普通圓柱齒輪在傳動中的應力和應變更小，承載能力更大。錯開1/2齒距比錯開1/3齒距齒輪傳動的應力和應變都要小，這可以使得錯開1/2齒距齒輪在傳動過程中可以得到更大的承載力和更小的變形。

3? 嚙合剛度分析

根據文獻[7]可得準靜態下嚙合剛度表達式為：

仿真完成后，提取主從動輪的轉角，得到動態傳遞誤差，計算出嚙合剛度。為了體現這種規律，引入無量綱嚙合時間 t/tc，t是絕對時間，tc是輪齒沿嚙合線移動一個分度圓法向齒距的時間。

從圖6可知，齒輪的嚙合剛度是周期性變化的，錯聯齒距的齒輪在嚙合時產生的沖擊和傳動的平穩性都要優于普通的圓柱齒輪，它可以降低齒輪運行時的突變程度，使傳動更加平穩，增加承載力;錯開1/2齒距齒輪與錯開1/3齒距齒輪相比在嚙合時產生的波動小，剛度更大，在傳動過程中更平穩，錯開1/2齒距齒輪比錯開1/3齒距齒輪更適用與傳動。

4? 結論

建立齒輪傳動模型，并通過有限元方法仿真得到錯聯齒輪傳動和普通圓柱齒輪傳動的應力與嚙合剛度曲線，仿真結果發現，輪齒嚙合過程中，由于嚙合剛度的時變性會產生頻率為嚙合頻率的周期性沖擊響應，錯聯齒輪在運行時的應力、應變和剛度變化都要優于普通圓柱齒輪;錯開1/2齒距齒輪與錯開1/3齒距齒輪相比承載能力和平穩性更好。采用錯開1/2齒距齒輪可以降低嚙合剛度的突變程度使運行更加平穩，減少振動，來達到優化齒輪振動特性的目的。

參考文獻：

[1]何育民，郝安幫.基于ANSYS workbench齒輪嚙合剛度計算及動力學仿真[J].沈陽工業大學學報，2020，42（02）：191-196.

[2]Zhan J X， Fard M， Jazar R. A CAD-FEM-QSA integ-ration technique for determing the time-varying me-shing stiffness of gear pairs[J]. M easurement， 2017， 100： 139-149.

[3]趙慶彬，劉海軍，李曉貞.面齒輪傳動嚙合剛度分析[J].機械傳動，2014（7）：6-9.

[4]卜忠紅，劉更，吳立言.斜齒輪嚙合剛度變化規律研究[J].航空動力學報，2010，25（04）：957-962.

[5]張雙偉，于文軍，金亮，等.基于有限元法的齒輪嚙合剛度分析[J].黑龍江科技信息，2016，24（24）：114-115.

[6]白恩軍，謝里陽，佟安時，等.考慮齒輪軸變形的斜齒輪接觸分析[J].兵工學報，2015，36（10）：1975-1981.

[7]郝安幫.嚙合剛度影響因素研究及齒輪動力學仿真[D].西安建筑科技大學，2018.