自控飛機大臂剛柔耦合動力學分析及疲勞壽命計算

趙九峰

（河南省特種設備安全檢測研究院，鄭州 450000）

引言

自控飛機是自控飛機類游樂設施中的一個品種，是根據模擬空戰情景設計的一種繞垂直軸旋轉、升降的游樂設備[1]。飛機圍繞火箭旋轉，并逐漸上升，游客在飛行中緊握操縱桿隨意升降，互相追逐，是游樂場所最受歡迎的項目之一。

在自控飛機運行過程中，座艙和乘客的起升和下降動作由大臂完成，大臂是自控飛機的主要承載部件，承受頻繁的交變載荷，疲勞破壞是大臂失效的主要原因，因此對自控飛機大臂進行疲勞校核就顯得尤為重要[2]。基于ANSYS Workbench有限元軟件平臺，在對大臂載荷特性分析的基礎上，利用虛擬樣機技術進行仿真分析，一般情況下，將機械系統中的構件當做剛性體來分析，當關注主要部件大臂在運行過程中的應力變化時，需要把大臂構件定義為柔性體[3]。因此建立自控飛機大臂起升系統的剛柔耦合的動力學仿真模型，在滿載起升工況下對大臂進行瞬態動力學仿真分析，獲取其在運行周期內最大應力的時間歷程曲線，并與傳統力學理論分析結果比較[4]，在此基礎上，對大臂進行疲勞壽命計算和疲勞校核，判斷大臂的疲勞強度是否符合要求。

1 載荷特性分析

1.1 運行原理

自控飛機是集升降、旋轉運動形式于一體的游樂設施，一般由底座、支架、大臂、氣缸飛機座艙等組成[5]。自控飛機的結構簡圖如圖1所示。

圖1 自控飛機結構簡圖

自控飛機由回轉和升降兩種運行形式組成，乘客通過站臺上下座艙，飛機座艙通過銷軸固定在大臂端部，乘客通過安全帶束縛在座位上，大臂通過銷軸固定在支架上，驅動部件通過小齒輪驅動支架底部的回轉支承，驅動大臂作水平旋轉運動。座艙內的乘客操作操控按鈕控制氣缸，升降支撐氣缸的往復運動驅動座艙的升降，座艙和乘客再隨大臂做升降和旋轉的復合運動[6]。

1.2 載荷特性分析

自控飛機工作時，乘人和座艙一邊繞回轉中心做旋轉運動，同時在氣缸的往復伸縮作用下，繞大臂根部做上下起伏運動，自控飛機大臂載荷示意圖如圖2所示。

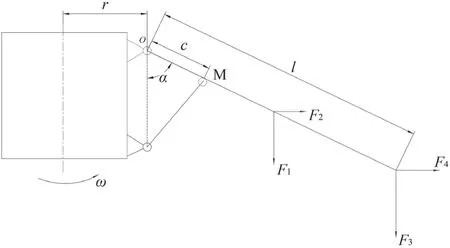
圖2 自控飛機大臂載荷示意圖

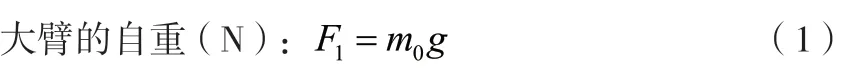
式中：

m0—大臂的質量，kg；

g—標準重力加速度，9.8 m/s2。

大臂繞回轉中心的離心力[7]（N）：

式中：

ω—自控飛機穩定運行時的旋轉角速度，rad/s；

l—大臂懸臂的等效長度，m；

r—大臂根部支點距回轉中心的半徑，m；

α—大臂的擺角，°。

式中：

1

m—座艙和乘人的質量，kg。座艙和乘客繞回轉中心的離心力（N）：

由合力矩定理可得大臂在氣缸支點M處的彎矩（Nm）：

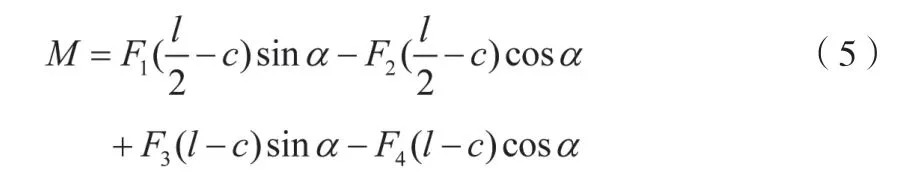
式中：

c—支點O與氣缸支撐點M的距離，m。

自控飛機大臂截面參數如圖3所示，則大臂的抗彎截面系數（mm3）：

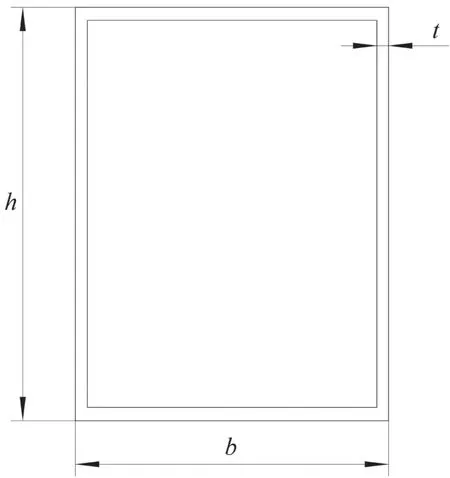
圖3 自控飛機大臂截面參數

式中：

b—大臂截面寬度，mm ；

h—大臂截面高度，mm；

t—大臂板厚度，mm。

則大臂的最大應力（MPa）：

2 理論計算

以某型號12臂自控飛機為例，單根大臂的質量0m=210 kg，大臂的等效長度l=5.0 m，滿載時座艙的質量 1m=280 kg（含2名乘客，每名乘客的質量為75 kg），支點O與氣缸支撐點M的距離大臂c=0.6 m，根部支點距回轉中心的半徑r=1.0 m，大臂M處截面寬度b=120 mm，高度h=220 mm，厚度t=8 mm。支點大臂的擺角α為變量，擺角α變化范圍為α=（30~130）°，自控飛機穩定運行時的旋轉角速度ω=0.6 rad/s。

大臂的自重由公式（1）可得：

大臂繞回轉中心的離心力由公式（2）可得：

座艙和乘客的自重由公式（3）可得：

座艙和乘客繞回轉中心的離心力由公式（4）可得：

由公式（5）可得大臂在氣缸支點M處的彎矩：

大臂的抗彎截面系數由公式（6）可得：

大臂的最大應力由公式（7）可得：

擺角α變化范圍為α=（30~130）°，分別取α的值：30 °、40 °、50 °、60 °、70 °、80 °、90 °、100 °、110 °、120 °、130 °，代入到方程組（8）可求得大臂不同擺角下的大臂應力如表1所示。由表1可知，大臂舉升過程中，隨著大臂擺角的增大，大臂最大應力的先增大后減小，當大臂擺角100 °時，大臂最大應力達到最大值66.0 MPa。

表1 大臂在不同擺角下的最大應力

3 瞬態動力學分析

3.1 大臂起升機構的剛柔耦合

ANSYS Workbench平臺根據研究對象不同對模型的剛度特性（Stiffness Behavior）進行剛柔耦合設置，并在構件之間添加運動關節（Joint）。使用軟件中的Transient Structural模塊，對自控飛機進行剛柔耦合的瞬態動力學分析，依據設備產品的尺寸，創建大臂、氣缸和部分支架的有限元實體模型，并在計算機上對起升機構進行幾何樣機的虛擬裝配，構建虛擬樣機模型[8]。其中大臂采用柔性體建模，其他部件采用剛性體建模。為了有效減少計算量，對支架和氣缸等剛性件進行簡化建模，為了得到大臂的應力解，對大臂進行精細化建模，采用4節點的殼單元（SHELL181），網格大小設置為30 mm，并使用四邊形為主的網格劃分[9]。座艙和兩個乘人總重量為280 kg，利用質量單元（Point Mass）,附加到大臂端部座艙安裝位置。大臂的有限元模型，如圖4（a）所示。

自控飛機整機設計壽命為15 年，支架固定在底座回轉支承上，施加旋轉幅（Revolute）。氣缸的伸縮帶動大臂繞支架上部擺動，同時氣缸繞支架下部和與懸臂連接處轉動，三個關節部位施加旋轉幅（Revolute）。氣缸桿與缸筒之間施加滑移副（Translational）。在氣缸桿與缸筒滑移副上施加驅動載荷（Joint Load），載荷類型為位移載荷（Displacement），支架旋轉幅施加恒定的轉速0.6 rad/s。Y負向施加等效重力加速度值為9.8 m/s2，大臂起升時間為9 s，在本次計算中，只考慮工作載荷，載荷與約束如圖4（b）所示。

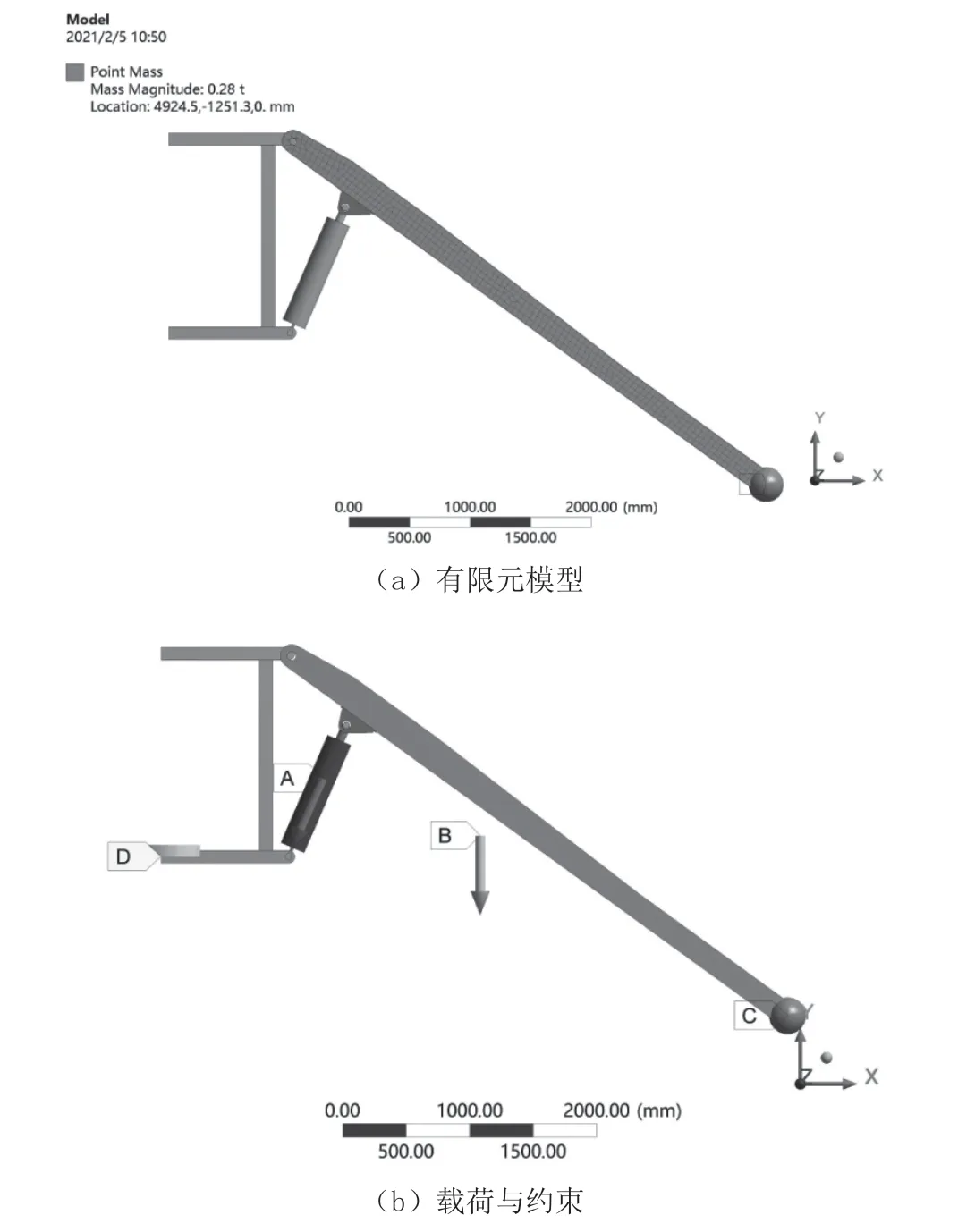
圖4 有限元模型及載荷

3.2 結果提取與分析

前處理完畢后進行仿真計算，定義仿真分析時間為9 s，最小時間步為0.05 s，使用直接求解法對起升機構進行剛柔耦合的動力學仿真。通過求解計算，提取大臂在起升過程中的最大應力，分析后進入后處理，得到大臂最大應力時間歷程曲線[10]，如圖5所示。

由圖5可知，在大臂擺動過程中，大臂的最大應力先增大后減小，最大應力值發生在大臂擺角108 °時，應力最大值為67.1 MPa，取擺角為108 °時的應力云圖，如圖6所示，危險區域主要集中在大臂下部氣缸支點部位。

圖5 大臂最大應力時間歷程曲線

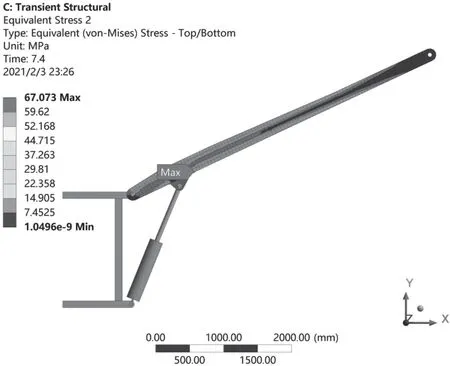
圖6 大臂擺角為108 °時的應力云圖

大臂最大應力理論計算數值與仿真結果進行對比，對比分析曲線如圖7所示。

由圖7可知，仿真結果基本與理論計算相符，大臂最大應力的最大值誤差不超過2 %，具有一定的參考比較性，可以證明有限元模型和剛柔耦合動力學仿真分析的可靠性和正確性[11]。兩組數據的變化趨勢基本一致，但在擺角起始和結束階段誤差較大，最大誤差約13 %，分析得出誤差產生的原因主要是理論計算未計入大臂的拉（壓）應力，在大臂擺角起始和結束階段，大臂和座艙自重沿大臂方向產生的拉（壓）應力最大，所以導致大臂擺角起始和結束階段誤差較大。

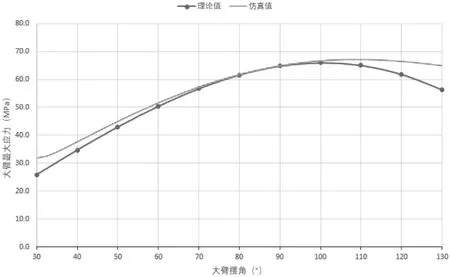
圖7 大臂最大應力對比分析曲線

4 疲勞分析

4.1 疲勞壽命計算方法

疲勞是游樂設施零件和部件的主要破壞形式，統計結果表明，在各類機械的斷裂事故中，大約有80 %以上是由于疲勞破壞引起的[12]。大臂是自控飛機中最主要的結構，它起到連接、支承座艙和乘客的作用，同時大臂不斷地起伏變化，同時繞著中心旋轉，承受著傳遞給它的各種力和力矩，必須有足夠的可靠性和疲勞壽命。

《鋼結構設計標準》16.1.3：疲勞計算應采用基于名義應力的容許應力幅法，容許應力幅應按構件和連接類別、應力循環次數以及計算部位的板件厚度確定[13]。《大型游樂設施安全規范》6.2.3.1：鋼結構構件及其連接的疲勞計算應符合GB 50017中關于疲勞強度計算的規定[14]。

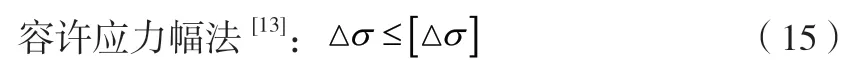
式中：

Δσ—疲勞應力幅，MPa；

[Δσ]—容許應力幅，MPa。

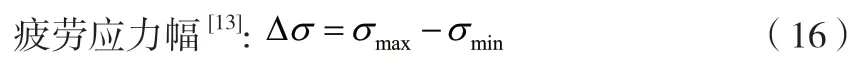
式中：

σmax—大臂最大應力值，MPa；

σmin—大臂最小應力值，MPa，大臂始終受壓，保守計算，σmin=0。

自控飛機大臂為箱型板焊接，板厚為8 mm，由《鋼結構設計標準》表K.0.2可知：焊接類別為Z5。

當應力幅 ?σ＜74 MPa時，對應疲勞次數：

式中：

C、β—構件與連接的相關系數，C=2×1012，β=3。

4.2 大臂疲勞壽命計算

根據自控飛機大臂剛柔耦合分析結果可以看出，大臂在運行過程中受到交變應力的作用，在大臂氣缸支點部位出現最大應力，最大應力遠小于其材料的抗拉極限，屬于高周疲勞[15]，因此大臂疲勞壽命計算時可采用基于名義應力的容許應力幅法。

由公式（16）可得疲勞應力幅：σ

? =67.1-0=67.1 MPa。

由于67.1 MPa≥74 MPa，由公式（17）可得疲勞次數：

自控飛機每小時運行10次（包括上下乘客時間，一個運行周期約6 min），每次運行大臂平均升降10次，則按照每天運行8 h，一年運行360天計算，自控飛機一年運行的次數為：10×10×8×360=2.88×105，可得疲勞壽命:

自控飛機整機的設計壽命為15年，可知大臂的疲勞壽命滿足設計要求。

需要指出的是，傳統自控飛機大臂疲勞壽命的計算方法，以座艙和乘客自重作為極限載荷，在大臂擺角為90 °計算大臂的彎曲應力（此時力臂最長，理論彎曲應力最大），實際大臂在起升和運行過程中，存在離心力和沿大臂方向的拉（壓）應力，因此傳統方法求得的極限彎曲應力是近似值。本文采取剛柔耦合的動力學分析方法，可以精確確定大臂的最大應力，從而精確計算大臂的疲勞壽命。

5 結論

以24座自控飛機為工程背景，根據合力矩定理，給出了大臂最大應力工程力學的計算公式，運用有限元軟件ANSYS Workbench軟件對大臂起升機構進行剛柔耦合的動力學仿真分析，通過仿真計算得出大臂最大應力的時間歷程曲線，并與理論計算結果進行對比，并依據仿真分析結果對大臂進行疲勞分析，計算結果表明：

1）自控飛機大臂在起升過程中最大應力隨著大臂擺角先增加后減小，仿真結果表明大臂擺角在108 °時，大臂最大應力達到最大。

2）大臂最大應力的仿真曲線與理論計算曲線進行對比，大臂最大應力的最大值誤差不超過2 %，驗證了建模、仿真的正確性及合理性。

3）由大臂關鍵部位應力的時間歷程曲線，基于名義應力的容許應力幅法對大臂進行疲勞壽命計算，結果表明大臂滿足使用壽命的設計要求。

剛柔耦合動力學分析方法可以在設備動態仿真過程中，實時輸出柔性部件關鍵部位的動應力曲線，從而保證計算結果的準確性和可靠性，提高疲勞計算的效率，其計算方法和結果可為游樂設施結構應力安全性評價和疲勞壽命計算提供參考，為后續工作對大臂進行結構優化研究，改善危險部位的應力水平，并提高結構抗疲勞強度具有現實意義。