不確定需求下鐵路集裝箱動態(tài)定價研究

唐慧敏，譚 雪，張小強，梁 越

不確定需求下鐵路集裝箱動態(tài)定價研究

唐慧敏1，譚 雪1，張小強1，梁 越2

（1. 西南交通大學，交通運輸與物流學院，成都 611756；2. 交通與城市規(guī)劃設計研究院，中鐵二院工程集團有限責任公司，成都 610031）

針對鐵路集裝箱運輸需求的不確定性，本文將傳統(tǒng)線性需求模型、多元logit需求模型與基于LSTM神經(jīng)網(wǎng)絡的深度學習需求模型進行對比，以鐵路承運企業(yè)利潤最大為目標函數(shù)建立集裝箱動態(tài)定價模型。首先，提取與集裝箱運輸需求相關(guān)的特征向量，采用梯度下降算法標定線性模型、多元logit模型參數(shù)和監(jiān)督式學習方法訓練LSTM神經(jīng)網(wǎng)絡。需求模型實驗顯示，與線性、多元logit模型相比，LSTM深度學習模型對集裝箱運輸需求的擬合精度更高。在此基礎(chǔ)上，設計精英選擇策略遺傳算法結(jié)合LSTM網(wǎng)絡的動態(tài)定價反饋機制求解集裝箱動態(tài)定價模型。實例結(jié)果表明，基于LSTM網(wǎng)絡的鐵路集裝箱動態(tài)定價模型能有效提升鐵路貨運企業(yè)收益。

鐵路運輸；動態(tài)定價；需求模型；收益管理；長短期記憶網(wǎng)絡；

0 引 言

2019年我國鐵路集裝箱發(fā)送量同比增長30%，但運輸收入增幅僅為13%[1]，鐵路集裝箱運輸在現(xiàn)有需求下有較大盈利空間。我國鐵路貨運價格長期以來一直遵循政府定價制度，公路運價則相對靈活，因此公路運輸在激烈的市場競爭下?lián)碛懈鼜姷挠芰Α橥苿予F路市場化改革，我國發(fā)布的《關(guān)于調(diào)整鐵路貨運價格進一步完善價格形成機制的通知》中指出應適當調(diào)整鐵路貨運價格，并建立運價上下浮動機制。當前已開放包括集裝箱運輸在內(nèi)的四項鐵路運輸價格，自此鐵路承運企業(yè)擁有更大的運輸自主定價權(quán)力。在此情況下，制定動態(tài)科學的集裝箱運輸價格是鐵路公司搶占貨運市場、提高運營收入的必然選擇。

動態(tài)定價是短期運營中管理需求、提升利潤最為有效的手段，其核心是以需求為導向在各類約束條件下制定最優(yōu)價格策略[2]。需求模型是價格策略優(yōu)化的必要前提，只有對需求進行準確的刻畫，才能制定有效的定價策略提升企業(yè)收益。部分研究直接假定需求滿足某類概率分布，例如：需求滿足泊松分布[3]、Beta分布[4]等，得到確定需求下的定價策略，此類型需求不考慮外在因素對需求的影響。大部分動態(tài)定價研究則是根據(jù)價格和需求相關(guān)因素的歷史數(shù)據(jù)，建立需求函數(shù)/價格響應函數(shù)。由于各因素之間相互作用關(guān)系事先是不確定的，因此一般先假設因素之間滿足線性或非線性的相互作用關(guān)系，確定需求形式后再求解模型參數(shù)。目前常見的需求模型有線性模型[5]、指數(shù)模型[6]、logit模型[7]。針對與鐵路集裝箱需求類似的時間序列，目前也有相關(guān)分析方式，例如：VAR[8]、ARIMA[9]等，但這類方法對數(shù)據(jù)平穩(wěn)性要求嚴格，且無法獲得因素對序列的影響及規(guī)律[10]。

鐵路運輸網(wǎng)絡復雜，貨物運輸需求不僅受政策、經(jīng)濟以及競爭的影響，還呈現(xiàn)地域性、趨勢性、季節(jié)性等復雜特征。上述傳統(tǒng)需求模型，提前對需求模型進行假設，然后再進行參數(shù)擬合。由于參數(shù)有限，難以全面描述運價與集裝箱量的變動關(guān)系及各因素間的耦合關(guān)系，據(jù)此需求模型制定的最優(yōu)定價可能并非最優(yōu)。深度學習方法以其強大的數(shù)據(jù)處理能力和學習能力，不假設任何數(shù)據(jù)間關(guān)系，已被廣泛用于挖掘各類數(shù)據(jù)之間的潛在聯(lián)系。目前已運用到電力需求與價格關(guān)系研究[11]等領(lǐng)域，能通過實際數(shù)據(jù)集監(jiān)督訓練直接實現(xiàn)綜合因素影響下的需求與電價之間的結(jié)構(gòu)化輸出。其中長短期記憶網(wǎng)絡（Long Short-term Memory, LSTM）作為一種特殊的循環(huán)神經(jīng)網(wǎng)絡（Recurrent Neural Network，RNN），是一種能處理時間序列的深度學習神經(jīng)網(wǎng)絡，對序列的非線性特征進行學習具有一定的優(yōu)勢。與基礎(chǔ)RNN相比，LSTM能避免因時間序列上節(jié)點距離較遠而產(chǎn)生的梯度爆炸和梯度消失的問題[12]，適合用于鐵路這種決策周期較長的行業(yè)。

本文建立鐵路集裝箱動態(tài)定價模型，選擇目前使用最廣泛的線性、logit模型及基于LSTM網(wǎng)絡的深度學習模型對鐵路集裝箱市場需求進行擬合，并設計遺傳算法求解最優(yōu)定價。

1 鐵路集裝箱動態(tài)定價模型

本模型著眼于鐵路運輸網(wǎng)絡中的集裝箱運輸班列，對OD間的集裝箱運輸銷售價格做出決策。基于收益管理的思想，以鐵路承運企業(yè)集裝箱利潤最大化為目標函數(shù)，以運力限制和政府制定的價格限制為約束條件，建立鐵路集裝箱動態(tài)定價模型。

1.1 符號說明

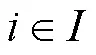
1.2 模型構(gòu)建

鐵路承運企業(yè)的運輸收入：

集裝箱運輸成本：

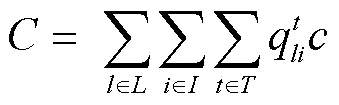
模型的目標函數(shù)為利潤最大：

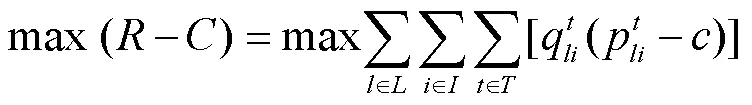
1.3 約束條件

各站點的實際發(fā)送量不超過各站點的集裝箱發(fā)送能力：

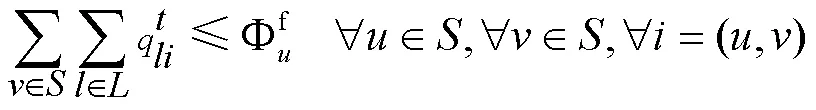
各站點的實際到貨量不超過各站點的集裝箱到達作業(yè)能力：

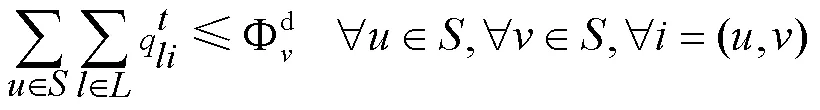
運價調(diào)整的上下限約束：

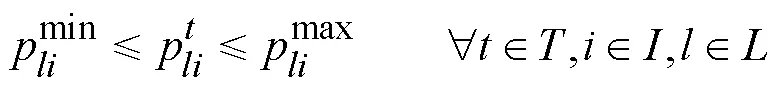
集裝箱實際運輸量不大于集裝箱需求量：

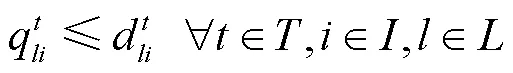
集裝箱運輸需求隨運輸定價的變動情況：

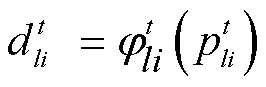
2 傳統(tǒng)需求模型與深度學習網(wǎng)絡需求模型

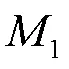
鐵路貨運系統(tǒng)具有動態(tài)性和不確定性[14]，在實際的鐵路運輸市場中需求與價格以及其他因素的影響關(guān)系也是不確定的。目前的研究大多假設價格和其他因素同需求呈線性或非線性關(guān)系，因此對需求模型的刻畫有多種參數(shù)形式。本節(jié)選擇典型線性、多元logit模型這類傳統(tǒng)需求模型以及基于LSTM網(wǎng)絡深度學習模型進行對比研究。

2.1 需求模型的影響因素

2.1.1 傳統(tǒng)需求模型的影響因素

2.1.2 深度學習網(wǎng)絡需求模型的影響因素

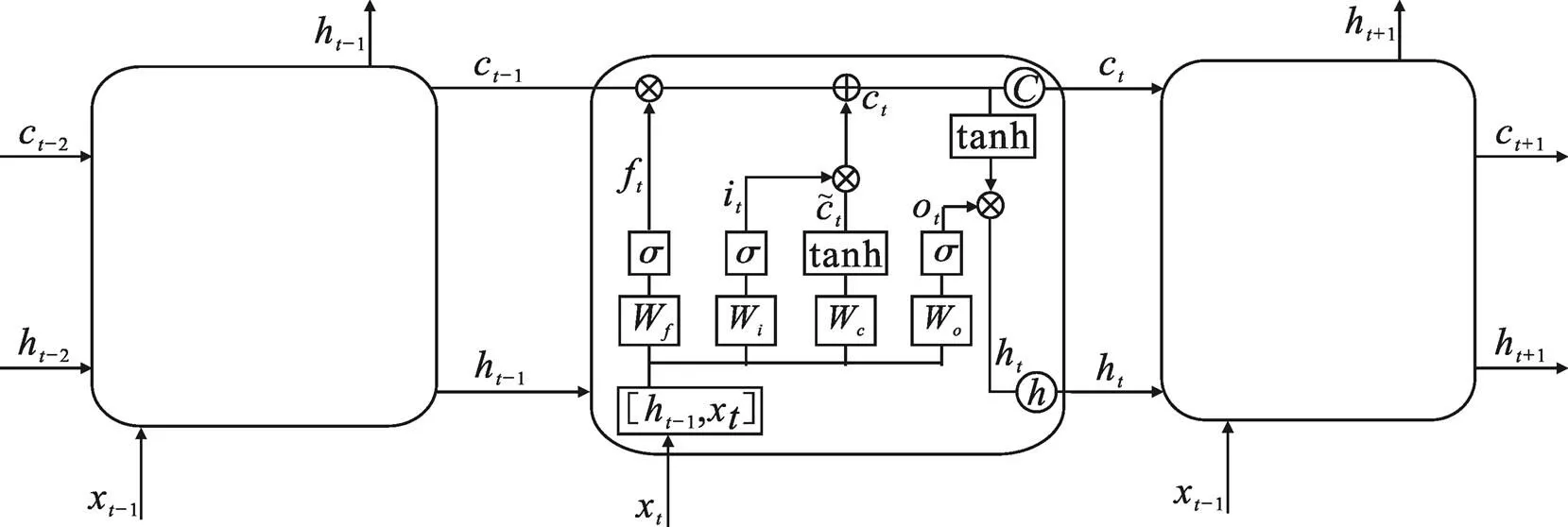
圖1 LSTM網(wǎng)絡及細胞結(jié)構(gòu)

2.2 三種需求模型

2.2.1 線性模型

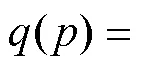
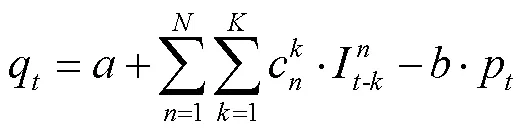
2.2.2 多元logit模型

目前應用較廣的需求模型是logit模型，該模型的優(yōu)勢在于它可以清晰地模擬需求分配過程，本節(jié)的研究問題為決策周期內(nèi)明確估計出客戶在鐵路運輸和公路運輸中選擇鐵路運輸?shù)母怕省８鶕?jù)多元logit模型的定義[12]可知：

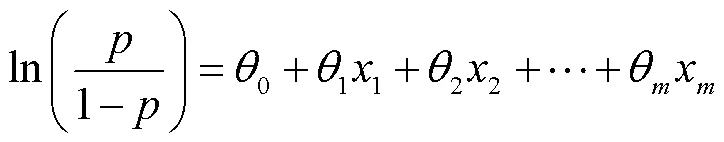
2.2.3 LSTM神經(jīng)網(wǎng)絡模型

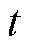
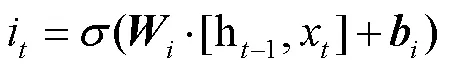
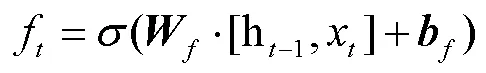
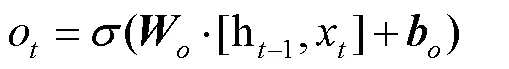
④ 隱藏向量的更新方式：

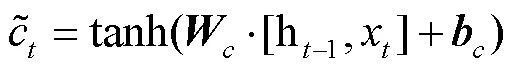
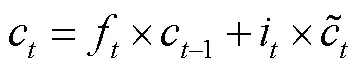
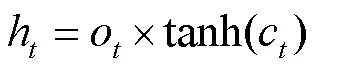
3 基于精英選擇策略的遺傳算法與LSTM反饋機制

當需求模型是線性或者logit形式時仍可采用求解線性/非線性規(guī)劃的經(jīng)典數(shù)學規(guī)劃方法。基于LSTM網(wǎng)絡構(gòu)建的模型無法給出具體表達式，無法使用常規(guī)求解方法。對此可采用遺傳算法（Genetic Algorithm, GA）搜索最優(yōu)解。本文將鐵路集裝箱動態(tài)定價模型的目標函數(shù)定為適應度函數(shù)，直接使用訓練后的LSTM網(wǎng)絡輸出端與遺傳算法相結(jié)合，形成反饋機制。

為簡化編碼過程，本文直接采用實數(shù)編碼方式，無須編碼解碼以便GA生成的初始種群可直接接入LSTM網(wǎng)絡輸入端口，LSTM網(wǎng)絡輸出的運量結(jié)果直接接入GA中計算個體適應度。但傳統(tǒng)GA在使用實數(shù)編碼時更易陷入迂回，導致運行速度不高也易陷入局部最優(yōu)解。因此本文采用基于精英選擇策略的遺傳算法（elitist model based on GA，e-GA）求解，結(jié)合LSTM網(wǎng)絡后，算法結(jié)構(gòu)如圖2所示。

具體步驟如下：

Step 3 計算初始種群對應的鐵路貨運需求。將初始種群數(shù)據(jù)輸入訓練后的LTSM網(wǎng)絡，求得需求數(shù)據(jù)。

Step 4 計算個體適應度函數(shù)值。使用ranking函數(shù)以鐵路集裝箱動態(tài)定價模型目標函數(shù)的負數(shù)來計算個體適應度，遵循目標函數(shù)的值越大適應度值越高。約束條件使用罰函數(shù)直接找到非可行解個體，修改其目標函數(shù)值為0。

Step 5 判斷適應度值是否穩(wěn)定。比較前后兩次輸出的適應度誤差是否小于預設誤差容限。若小于誤差容限則輸出結(jié)果，否則轉(zhuǎn)至下一步。

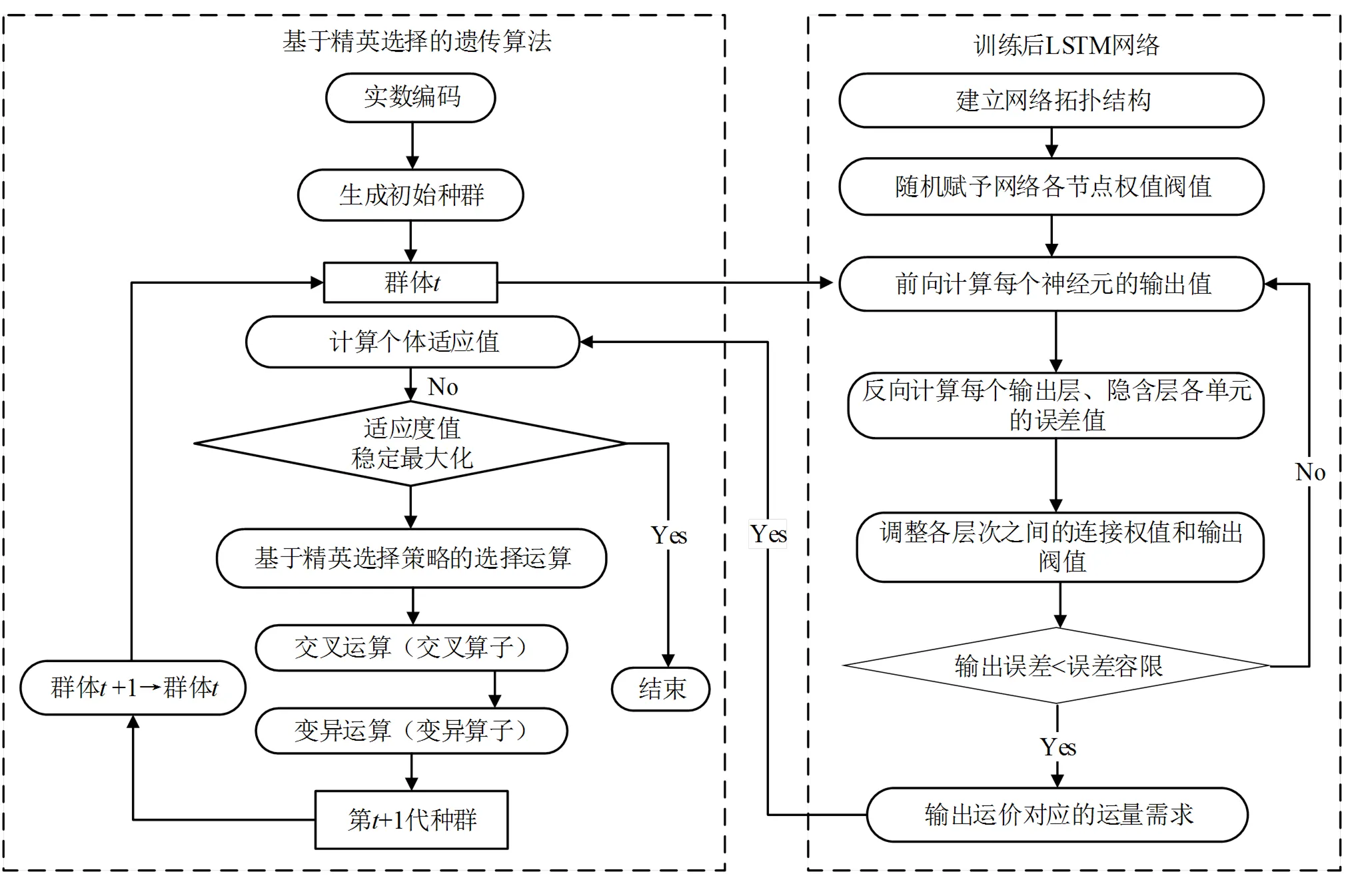
圖2 算法流程圖

Step 6 選擇算子。精英復制選擇，將當前適應值大于下一代最佳個體適應值的精英個體，建立精英個體的索引直接復制到下一代。

Step 7 交叉算子和變異算子。本文采用多點交叉，隨機生成多個交叉點，并在交叉點進行交換。變異算子選擇染色體片段逆轉(zhuǎn)變異算子，與交叉算子一起完成種群的進化。

4 實例分析

4.1 鐵路集裝箱需求模型

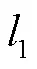
由圖3（a）可知，鐵路集裝箱量以年為單位呈周期性變化，有明顯的季節(jié)性特征，2015年后總體運量驟減。運價總體變動平緩，2017年前無法判斷運價與運量之間的彈性。圖3（b）表明2017年運價調(diào)整對應運量變化，說明鐵路運輸市場客戶對運輸價格敏感。同時根據(jù)整體走勢可知，鐵路集裝箱運量變化趨勢復雜，無法直接判斷其實際符合的需求模型，因此在本節(jié)將使用上文構(gòu)建的線性、多元logit模型以及LSTM網(wǎng)絡需求模型對數(shù)據(jù)進行擬合。

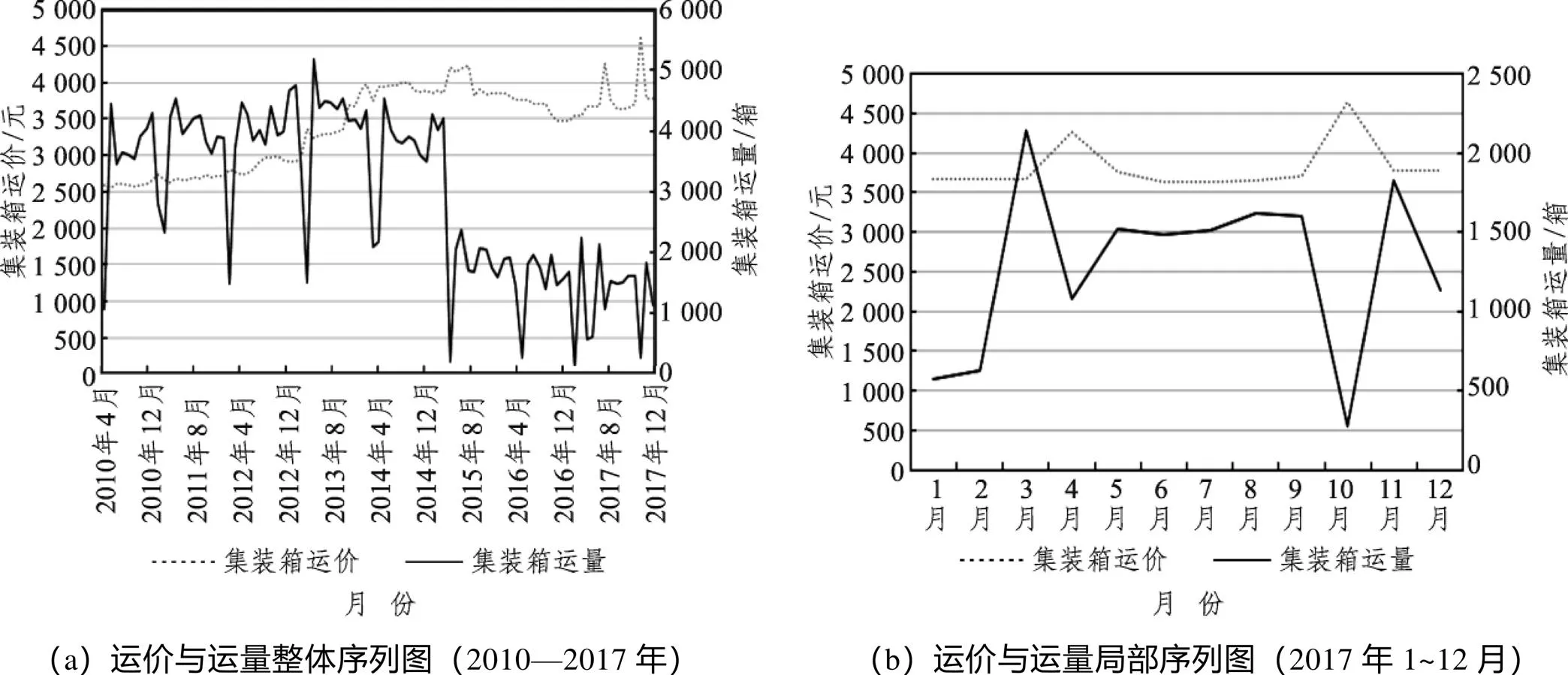
圖3 運量與運價序列圖

4.1.1 特征分析

為驗證輸入指標的有效性，本節(jié)對所選取指標的有效性進行評估和篩選。因為其中經(jīng)濟指標包括廣東省GDP、四川省GDP、廣東第一產(chǎn)業(yè)產(chǎn)值、廣東第二產(chǎn)業(yè)增加值；競爭指標包括廣東省公路集裝箱量、道路集裝箱運價指數(shù)，以及該路局鐵路集裝箱運輸價格和鐵路集裝箱運量。對上述指標與鐵路集裝箱運量做相關(guān)性分析，得相關(guān)系數(shù)如圖4所示。

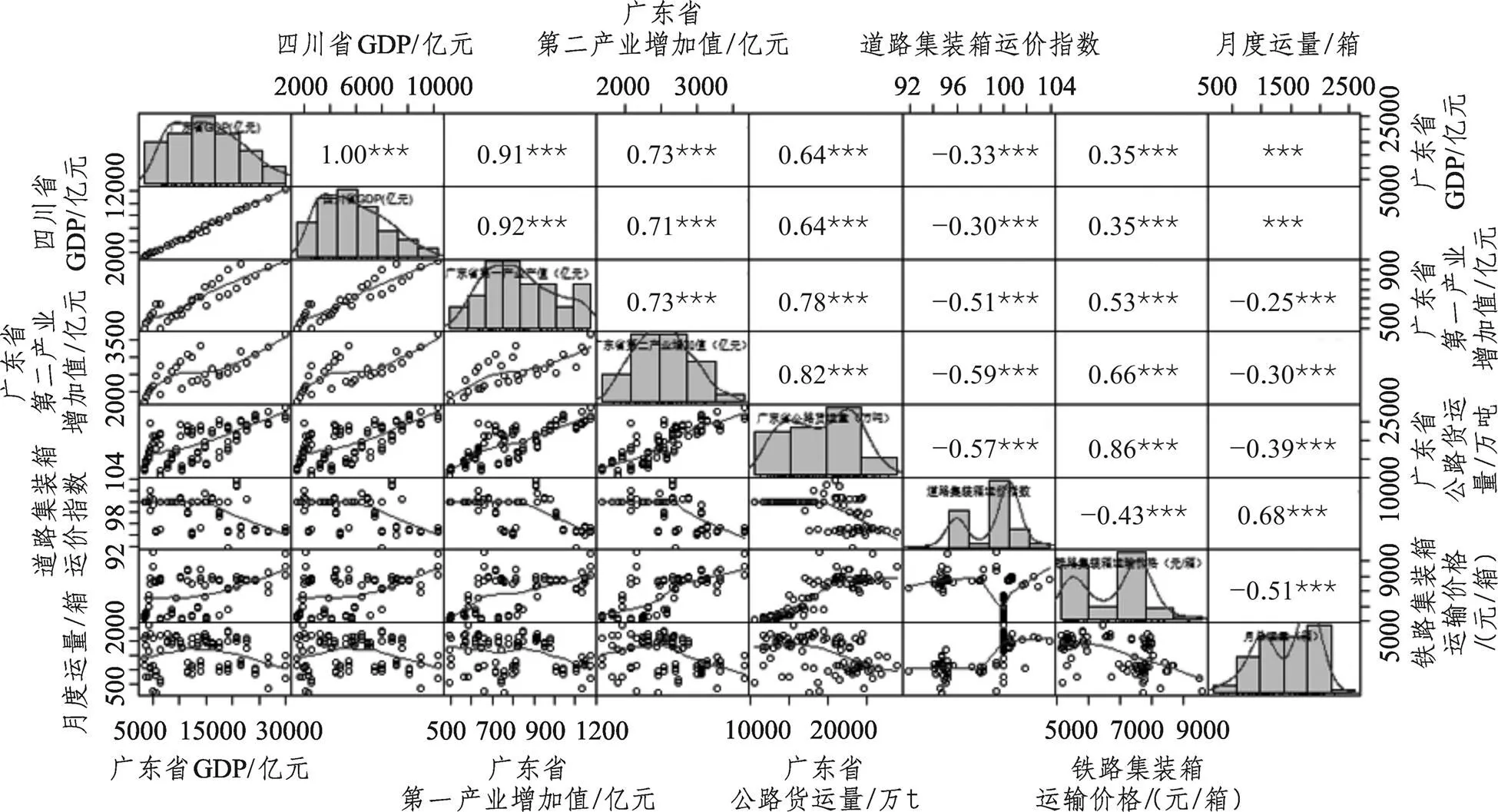
圖4 相關(guān)系數(shù)圖

數(shù)值代表相關(guān)系數(shù)，星號代表顯著程度。由圖4可知，兩省份GDP與集裝箱量的相關(guān)性不顯著，可能是由于GDP數(shù)據(jù)為季度數(shù)據(jù)而非月度數(shù)據(jù)，無法體現(xiàn)GDP在月度間的變化情況。因此確定輸入特征為：宏觀經(jīng)濟指標（廣東省第一產(chǎn)業(yè)產(chǎn)值、廣東省第二產(chǎn)業(yè)增加值）、競爭因素指標（廣東省—四川省公路集裝箱量、公路集裝箱價格指數(shù)、鐵路集裝箱運價、鐵路集裝箱運量）。

4.1.2 數(shù)據(jù)處理

為消除數(shù)據(jù)量綱對結(jié)果的影響，對原數(shù)據(jù)進行預處理。數(shù)據(jù)預處理包括數(shù)據(jù)歸一化、劃分訓練集測試集和時間序列構(gòu)建。訓練前將數(shù)據(jù)如式（19）進行歸一化處理，分為訓練集（2010—2016年）和測試集（2017年），并構(gòu)建時間序列：

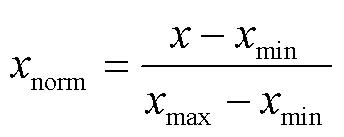
4.1.3 訓練方法

線性與多元logit模型是典型的參數(shù)模型，大多采用直接令原函數(shù)對該參數(shù)的偏導值為0的方式得到該參數(shù)的解析解，但易出現(xiàn)過擬合的問題，需要添加正則項等方式進行優(yōu)化。

因此本文采用梯度下降法，結(jié)合Early Stopping方法求解線性及多l(xiāng)ogit模型的參數(shù)矩陣。當前后兩次迭代時損失函數(shù)的差值降至最小時，輸出當前對應的參數(shù)值。LSTM神經(jīng)網(wǎng)絡通過Early Stopping方法和Adam算法確定參數(shù)取值。選擇均方誤差MSE（Mean Square Error）作為損失函數(shù)對各模型進行訓練：

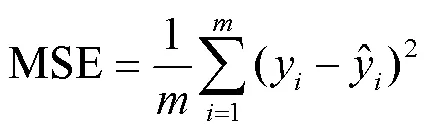
4.1.4 評估指標

考慮評價標準在實際情況中的現(xiàn)實意義，本文選擇均方根誤差RMSE（Root Mean Square Error）作為模型的評價指標：

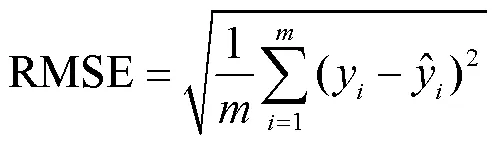
4.1.5 實驗結(jié)果

本文LSTM神經(jīng)網(wǎng)絡的超參數(shù)取值：一層LSTM循環(huán)層、兩層全連接隱藏層、一層dropout層和一層dense層，具體參數(shù)為5個神經(jīng)元、10個神經(jīng)元、隨機丟失概率（0.1）和1個神經(jīng)元，激活函數(shù)采用relu函數(shù)。將線性、多元logit模型和LSTM網(wǎng)絡在測試集中的表現(xiàn)結(jié)果進行比較，并分析價格與需求之間的動態(tài)關(guān)系，測試集上評價指標結(jié)果如表1所示。

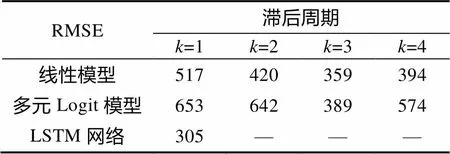
表1 結(jié)果評價指標

選擇線性函數(shù)（= 3）、多元logit模型（= 3）以及LSTM神經(jīng)網(wǎng)絡需求模型在2017年測試集的真實值與計算值進行測試，繪圖如圖5所示。

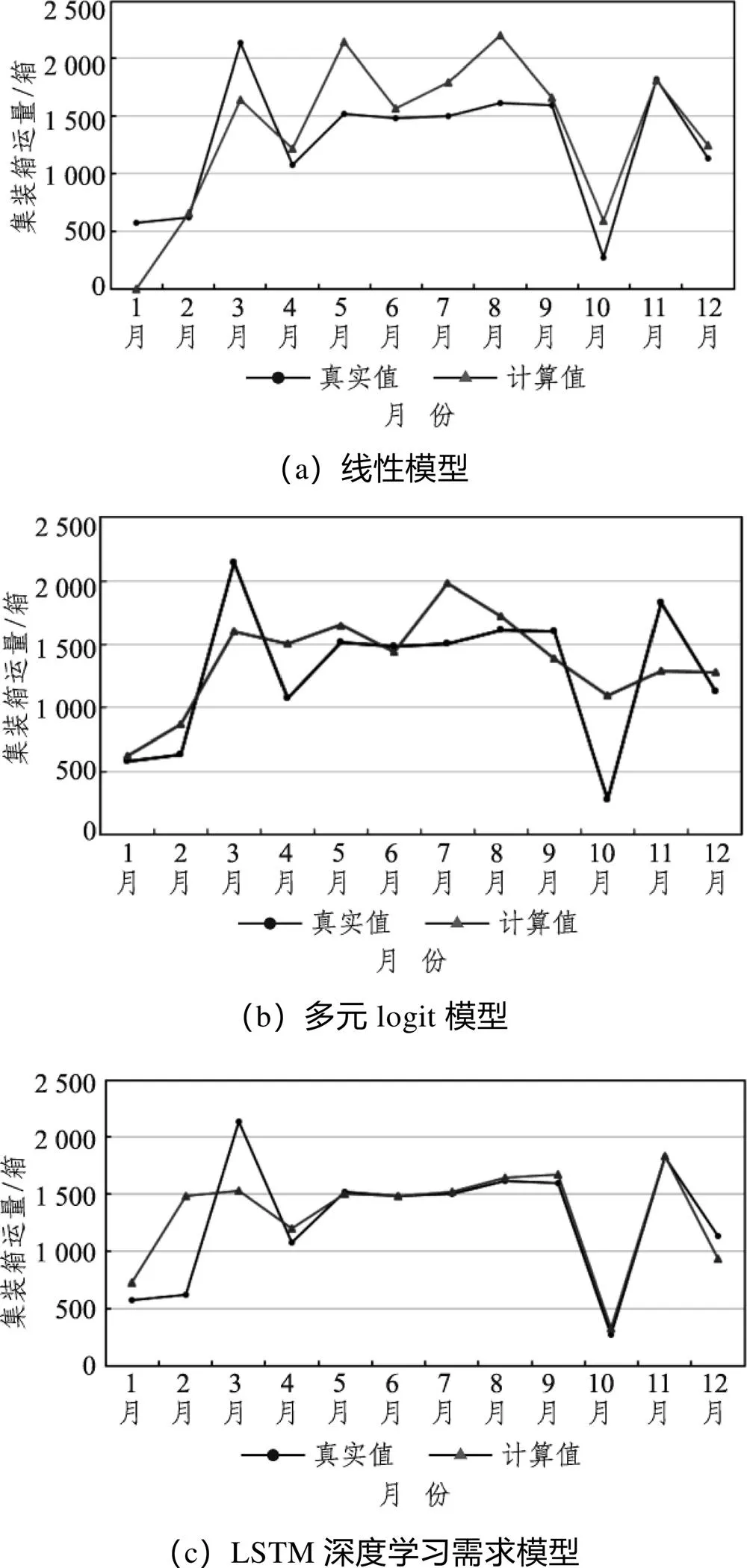
圖5 測試集集裝箱量中真實值及計算值對比

綜上，訓練后的LSTM神經(jīng)網(wǎng)絡需求模型對鐵路集裝箱市場的擬合程度最好。由于LSTM需求模型是非參數(shù)化模型，無法直接分析其各因素間的耦合關(guān)系。因此通過控制價格不變，其他因素參照實際情況輸入，分析集裝箱運量在運價不變時的波動情況。保持2017年月度其他影響因素值不變，在價格區(qū)間[2 400, 5 000]元內(nèi)變動鐵路集裝箱運輸價格，訓練后的LSTM神經(jīng)網(wǎng)絡輸出對應集裝箱需求，選擇部分月份制圖如圖6所示。

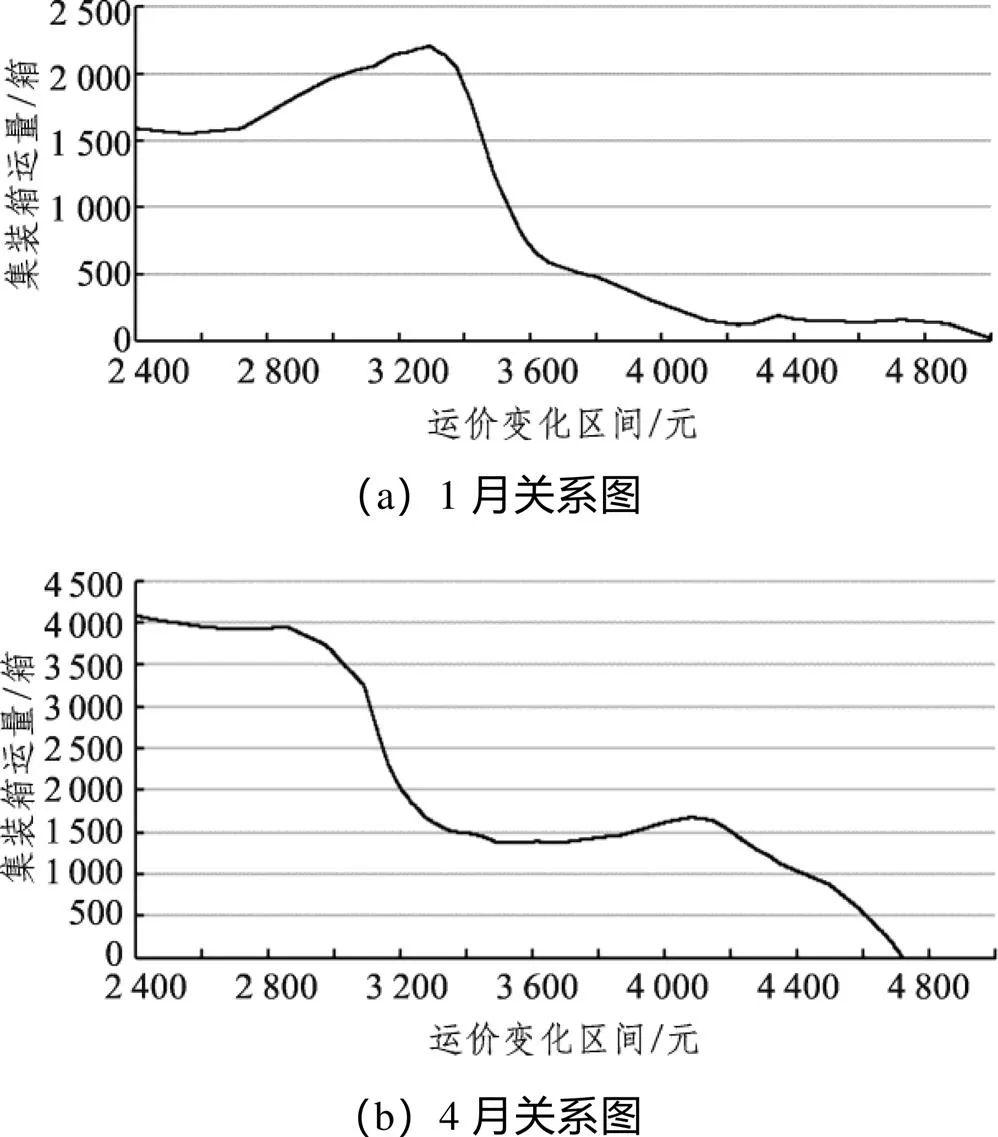
圖6 運價與集裝箱需求關(guān)系圖

如圖6可知：

（1）運價和運量的整體趨勢是隨著價格的上升運量下降，但并不是光滑的負相關(guān)函數(shù)。且運量在運價增加時有小范圍上升，反映了需求上升的時候價格也上升的經(jīng)濟現(xiàn)象。對此傳統(tǒng)需求函數(shù)較難描述和預測此類市場變化，而LSTM深度學習網(wǎng)絡能挖掘出此類潛在的市場現(xiàn)象。

（2）不同月份運價的變化對應不同的運量變化區(qū)間和趨勢，說明不同時間客戶對運價的敏感度不同，因此運輸需求無法用某一固定參數(shù)函數(shù)進行描述。

4.2 定價模型求解及結(jié)果分析

根據(jù)目前該路局的運營計劃，該路局每月更新一次集裝箱運輸定價，12個月為一個決策周期。使用第3節(jié)中建立的基于精英選擇策略的遺傳算法與LSTM網(wǎng)絡反饋機制，將上述已分別訓練的LSTM網(wǎng)絡接入基于精英選擇的遺傳算法端口。在運價上下限區(qū)間[2 400, 5 000]中隨機生成運價并輸入LSTM網(wǎng)絡中，然后輸出對應的集裝箱貨運需求。遺傳算法種群規(guī)模設置為50，最大遺傳代數(shù)為500。在遺傳算法模塊并行計算優(yōu)化上述OD，輸出不同區(qū)間上不同貨物在不同時間的集裝箱運輸最優(yōu)定價及總收入、利潤。

由圖7可知，目前鐵路運價還有較大的調(diào)整空間，在運營前期制定價格時可采取適當向下調(diào)整運價的策略，以吸引客源；當運輸旺季時可適當提升價格，控制需求來減少運輸成本進而提升收益。

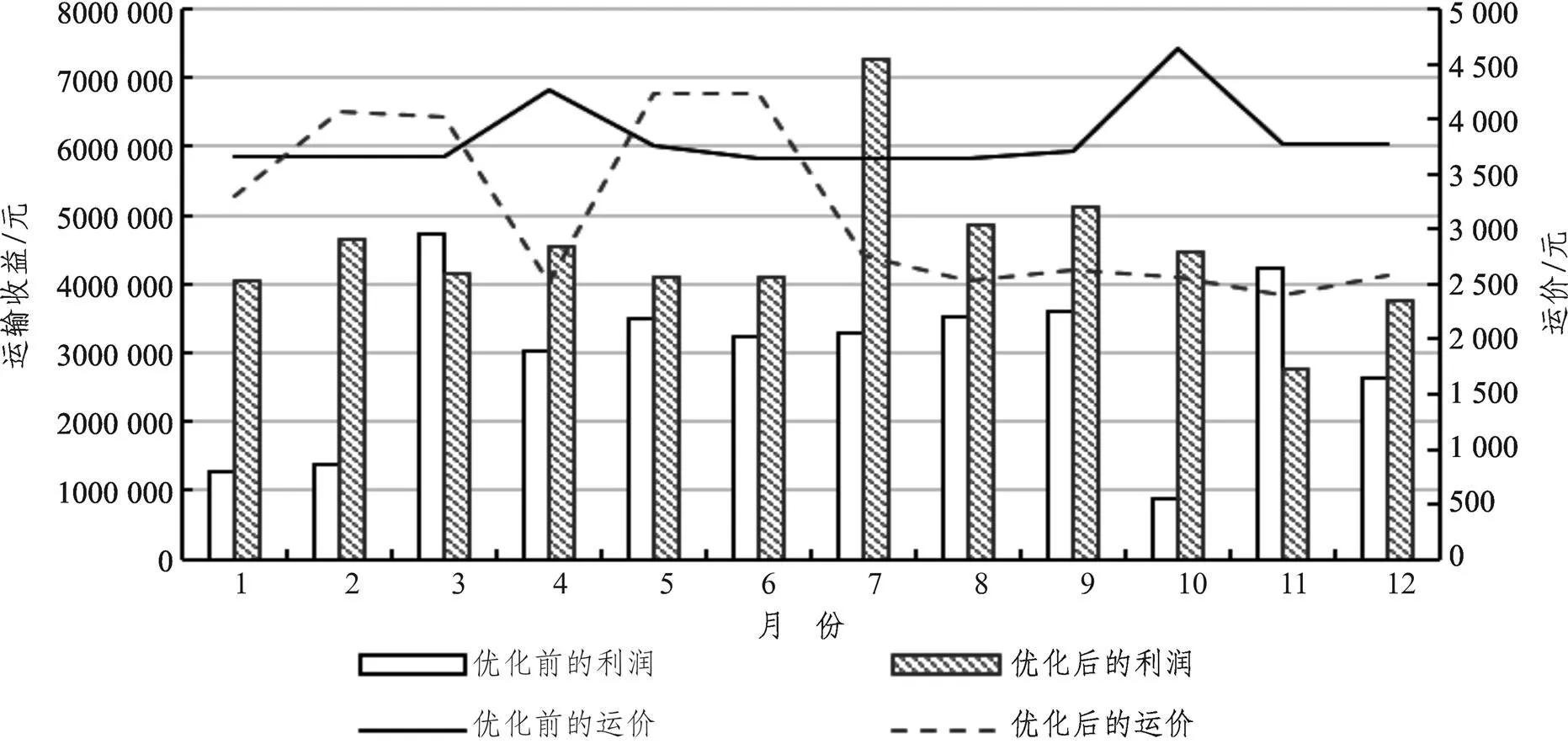
圖7 優(yōu)化前后對比圖

5 結(jié) 論

本文通過線性、logit模型與LSTM神經(jīng)網(wǎng)絡深度學習模型對鐵路集裝箱需求進行擬合，實驗發(fā)現(xiàn)線性、logit函數(shù)等參數(shù)函數(shù)由于其參數(shù)的有限性，對真實市場的擬合情況不佳。而LSTM深度學習模型的歷史數(shù)據(jù)在測試集中誤差最小，可挖掘市場潛在的變化趨勢和各因素的變化關(guān)系，擁有較好的泛化能力。案例分析表明基于深度學習需求模型的動態(tài)定價策略可用于企業(yè)需求管理，挖掘出不同時期需求的價格彈性，制定更加合理的價格策略。在接下來還可針對當日實時定價進行研究，將天氣、客戶瀏覽、節(jié)假日等信息納入深度學習模型的訓練，進一步探究市場變化和客戶行為，優(yōu)化日定價策略。

[1] 劉清芳. 鐵路集裝箱運輸發(fā)展對策探討[J]. 鐵道運輸與經(jīng)濟, 2020, 42(9): 34-39.

[2] TALLURI B, RYZIN G. The theory and practice of revenue management[M]. Berlin: Springer, 2005.

[3] 姜愛萍, 夏浩, 高峻峻, 等. 電力物資復合泊松需求下的最優(yōu)訂貨量[J]. 工業(yè)工程, 2016, 19(3): 90-95.

[4] GRAF M, KIMMS A. An option-based revenue management procedure for strategic airline alliances[J] European Journal of Operational Research, 2011, 215(2): 459-469.

[5] 宋文波, 趙鵬, 李博. 高速鐵路單列車動態(tài)定價與票額分配綜合優(yōu)化研究[J]. 鐵道學報, 2018, 40(7): 10-16.

[6] GALLEGO G, RYZIN G V. Optimal dynamic pricing of inventories with stochastic demand over finite horizons[J] Management Science, 1994, 40(8): 999-1020

[7] 方園, 樂美龍. 基于強化學習的平行航班動態(tài)定價[J]. 華東交通大學學報, 2020, 37(1): 47-53.

[8] 文書生, 葉懷珍. 基于VAR模型的中國鐵路集裝箱需求實證分析[J]. 重慶大學學報: 自然科學版, 2007(10): 152-158.

[9] 張立欣, 張艷波, 楊翠芳. 基于X11-ARIMA模型的鐵路集裝箱周轉(zhuǎn)量分析[J]. 數(shù)學的實踐與認識, 2018, 48(17): 154-161.

[10] 景楠, 史紫荊, 舒毓民. 基于注意力機制和CNN- LSTM模型的滬銅期貨高頻價格預測[J/OL]. 中國管理科學: 1-13[2020-10-13]. https: //doi. org/10. 16381/j. cnki. issn1003-207x. 2020. 0342.

[11] XU H, SUN H, NIKOVSKI D, et al. Learning dynamical demand response model in real-time pricing program[C]// 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference(ISGT), Washington: IEEE, 2019: 1-5.

[12] 王鑫, 吳際, 劉超, 等. 基于LSTM循環(huán)神經(jīng)網(wǎng)絡的故障時間序列預測[J]. 北京航空航天大學學報, 2018, 44(4): 772-784.

[13] 張小強, 劉丹, 陳兵, 等. 競爭環(huán)境下鐵路集裝箱班列動態(tài)定價與開行決策研究[J]. 鐵道學報, 2017, 39(2): 17-23.

[14] 高醒, 李夏苗, 彭鵬. 鐵路貨運量預測過程中的關(guān)鍵技術(shù)分析[J]. 科技和產(chǎn)業(yè), 2018, 18(5): 1-8, 62.

Research on Dynamic Pricing of Railway Containers under Uncertain Demand

TANG Hui-min1, TAN Xue1, ZHANG Xiao-qiang1, LIANG Yue2

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. Transport and Urban Planning and Design Research Institute, China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China)

In this study, the traditional linear demand function and the multi-logit demand model with the deep learning demand model, based on the long short-term memory (LSTM) neural network, are compared, considering the uncertainty of the railway container transportation demand model. This study maximizes the profit of the railway carrier by establishing a dynamic container pricing model. We extract the feature vectors related to the container freight demand, use the gradient descent method to solve the linear function and logit model parameters, and train the LSTM neural network through the supervised learning method. The results show that LSTM is more accurate relative to demand than linear and the logit function. We design an e-GA combined with the dynamic pricing feedback mechanism of LSTM to solve the pricing model. Finally, calculations based on actual cases show that the dynamic pricing model of railway containers based on LSTM can effectively increase the revenue of railway freight enterprises.

railway transportation; dynamic pricing; demand model; revenue management; long short-term memory

1672-4747（2021）03-0133-10

U294.3；F532.5

A

10.19961/j.cnki.1672-4747.2020.10.005

2020-10-13

2020-12-09

2021-06-28

四川省科技廳軟課題（2020JDR0127）；成都市科技局軟科學課題（2020-RK00-00102-ZF）

唐慧敏（1996—），女，漢族，四川眉山人，碩士，研究方向為鐵路運輸、深度學習，E-mail：744766576@qq.com

張小強（1975—），男，漢族，江西石城人，副教授，研究方向為鐵路運營管理、人工智能，E-mail：xqzhang@swjtu.edu.cn

唐慧敏，譚雪，張小強，等. 不確定需求下鐵路集裝箱動態(tài)定價研究[J]. 交通運輸工程與信息學報，2021, 19(3): 133-142.

TANG Hui-min，TAN Xue，ZHANG Xiao-qiang, et al. Research on Dynamic Pricing of Railway Containers under Uncertain Demand [J]. Journal of Transportation Engineering and Information, 2021, 19(3): 133-142.

（責任編輯：李愈）