任務間共享和特有結構分解的多任務TSK 模糊系統建模

趙壯壯，王駿，潘祥，鄧趙紅，施俊，王士同

（1.江南大學 人工智能與計算機學院，江蘇 無錫 214122;2.上海大學 通信與信息工程學院，上海 200444）

模糊邏輯和模糊推理被用來描述知識和表達的不確定性。而模糊系統就是由模糊邏輯和模糊推理發展而來的。相比于傳統的機器學習模型，模糊系統能夠更準確地描述和估計現實中不確定的復雜非線性系統模型[1-4]。近年來，學者們提出了眾多的模糊系統建模方法，其中TSK 模糊系統因其能夠將非線性系統轉化為多個局部線性結構的逼近，而成為最受歡迎的模型之一[5-7]。

TSK 模糊系統由若干條模糊規則構成，每條模糊規則由前件和后件組成。傳統的模糊規則構建依靠專家經驗。近年來，數據驅動的模糊規則構建方法受到了充分的研究。通常可以劃分為兩個步驟：一是使用某種劃分規則將訓練數據分為若干子體來提取規則前件參數，在實際建模中，通常使用聚類來實現；二是學習優化后件參數，從機器學習的角度，可以視為一個線性回歸問題[8-11]。

TSK 模糊系統建模是重要的有監督學習的過程，因此需要充分的訓練數據。然而，在很多實際應用中，樣本數據經常是有限的高維數據，這就不可避免導致了模型的過擬合問題。而多任務學習可以從其他任務中獲取相關信息，一定程度彌補訓練數據不足的問題，進而提高模型的學習性能[12-17]。在多任務建模中，任務之間往往具有明顯的相關性，并存在著共享信息，因此充分利用多個任務間的共享信息進行多任務模糊系統建模，有助于提高每個任務的泛化性能。例如，Jiang等[18]提出了一種利用潛在任務間關系信息的多任務模糊系統，該方法為多個任務學習了一個共享的后件參數來表示任務間的共享信息。然而，這些方法都只著重于任務間后件參數的共享結構，而忽視了如何利用各任務的自身特點。

鑒于此，本文提出了一種新型多任務TSK模糊系統建模方法，在挖掘多任務間共享信息的同時，保留單個任務的特殊性。該方法將多任務的后件參數矩陣分解為共享參數矩陣和特有參數矩陣兩個部分：共享參數矩陣表示了任務之間共享的結構信息，而特有參數矩陣保留了每個任務的不同于其他任務的差異信息。本文通過為共享參數矩陣和特有參數矩陣分別引入低秩和稀疏約束來實現這一目標。

1 多任務TSK 模糊模型的基本原理

經典的單任務TSK 模糊系統利用多個局部線性子模型來近似非線性模型。而多任務模糊系統就是多個單任務模糊系統的聯合優化。在多任務設置中和D分別表示任務、樣本和特征的數量，其t中=1Nt表示任務t的樣本數量。對于任意輸入向量其表示任務t的一個樣本的特征向量，其中是向量xt的第d變量。

因此，任務t的第m個規則可以表示為：

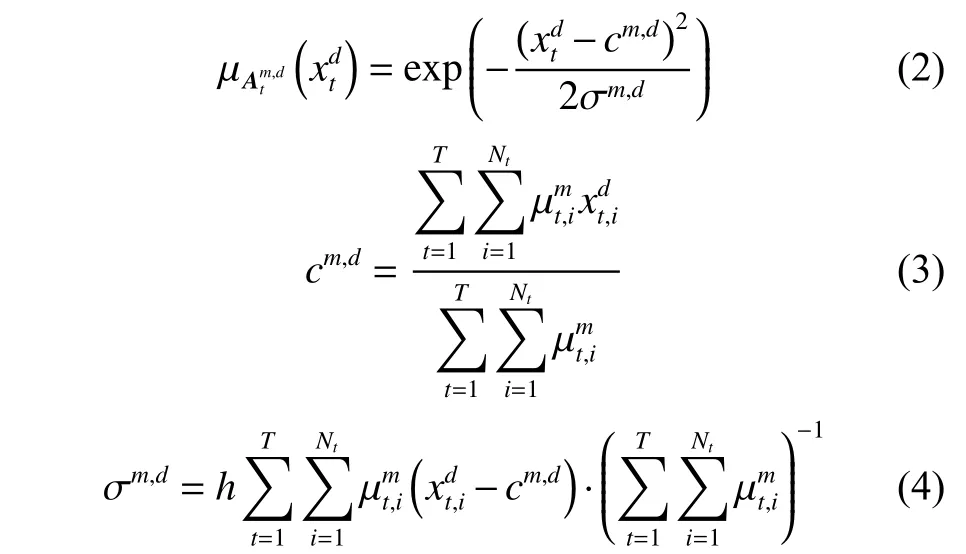
為方便計算，本文為多任務TSK 模糊模型進一步定義W=(w1,w2,···,wT)∈R(D+1)M×T，表示多任務模糊模型的后件參數聯合矩陣。所以，基本多任務模糊系統的目標函數可以表示為

2 任務間共享和特有結構分解的多任務TSK 模糊系統建模新方法

本節在基本多任務模糊系統的基礎上，進一步提出新型多任務模糊系統建模方法。考慮到多任務之間是相互關聯的，因此可以認為多個任務的模型參數包含著潛在的共享信息；另一方面，各任務的模型參數中都包含了自身不同于其他任務的特有信息。如圖1 所示，本文將各后件參數聯合矩陣W分解為共享參數矩陣V和特有參數矩陣E，即：

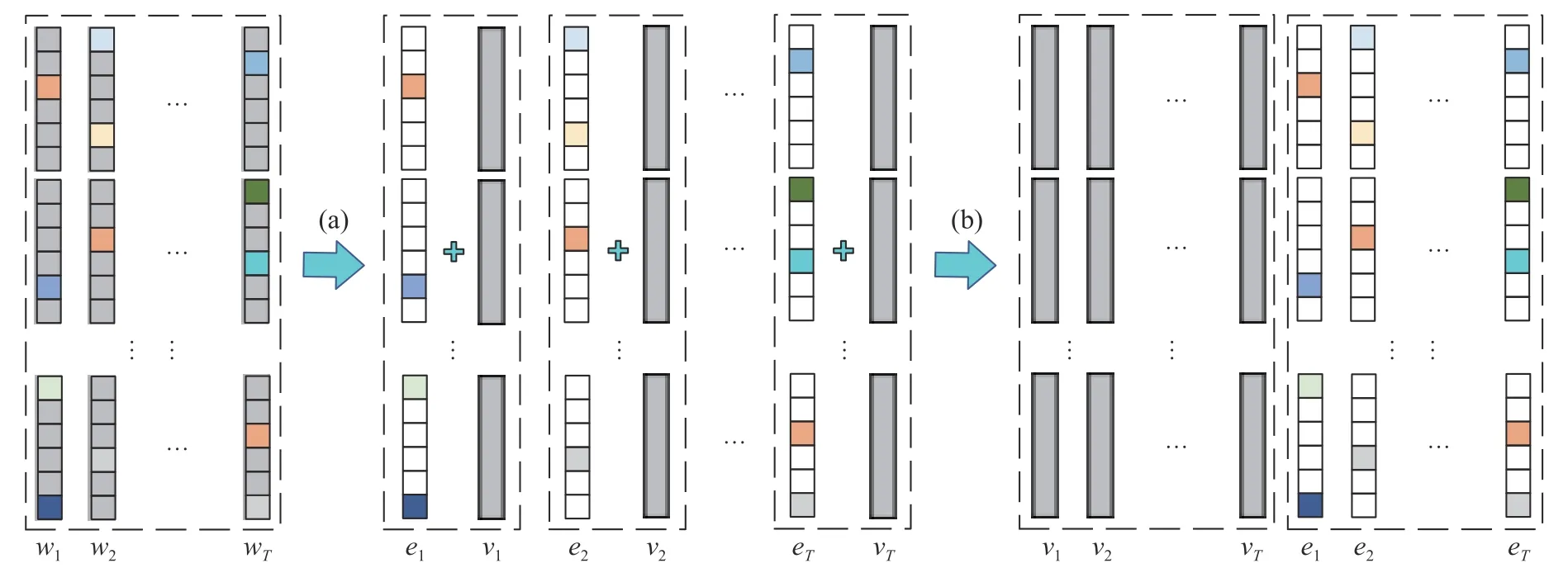
圖1 后件參數矩陣 W=(w1,w2,···,wT) 可以拆分為低秩部分 V=(v1,v2,···,vT) 和稀疏部分E=(e1,e2,···,eT)Fig.1 The consequent parameter matrix W=(w1,w2,···,wT) can be decomposed into the low-rank component V=(v1,v2,···,vT)and the sparse componentE=(e1,e2,···,eT)

共享參數矩陣V包含了任務之間的共享參數信息，這種共享信息是指同一個特征在不同的任務中發揮相似的作用。具體表現在，如果某個特征在任務i中被賦予了一個較高的權重值，那么它在相關任務j中也將被賦予較高的權重，反之亦然，即對應于任務i和任務j的共享參數vi和vj是相似的。因此，共享參數矩陣V具有低秩性，本文通過引入核范數來實現對共享參數矩陣V的低秩約束特有參數矩陣E表示各項任務不同于其他任務的特有信息，這種特有信息體現在某一特征在不同任務中發揮不同的作用，即特有參數矩陣E是行稀疏的，本文通過引入正則化項實現行稀疏。

所以，通過對后件參數聯合矩陣的分解，再分別施加低秩和行稀疏約束，在多任務建模中兼顧多任務之間共享信息和特有信息的作用，提出了任務間共享和特有結構劃分的多任務TSK 模糊系統的目標函數，表示如下：

式中：α和β 是正則化參數，用于調節共享參數和特有參數在模型訓練中發揮的作用，參數越大，懲罰力度越大。

3 目標函數優化

本文使用增廣拉格朗日乘子法[19-20]求解式(10)提出的最優化問題，其增廣拉格朗日目標函數為

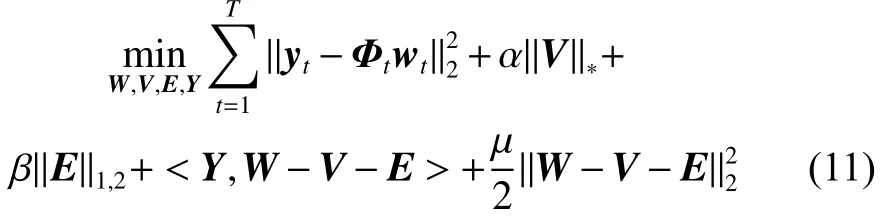
式中：Y∈R(D+1)×T是拉格朗日乘子矩陣，〈·,·〉 表示兩個矩陣的內積運算。為便于計算，使用LADMAP 方法[21]將目標函數重新表示為

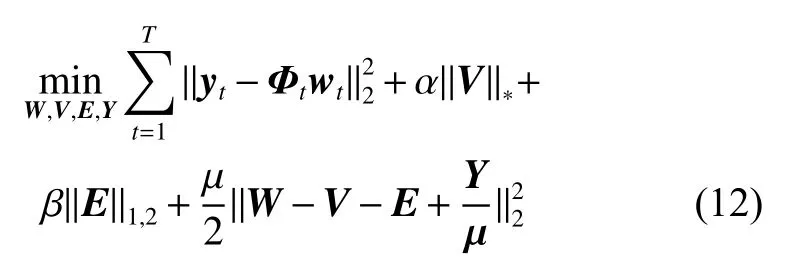
這是一個包含W、V、E、Y4 個優化變量的最優化問題，所以本文交替使用其他變量的固定值迭代優化每個變量，原問題被轉化為下面若干個子問題：

1) 固定V、E、Y，式(12)化為如下目標函數：

對wt求導，并令其等于 0，整理之后，可以通過式(14)獲得wt的解：

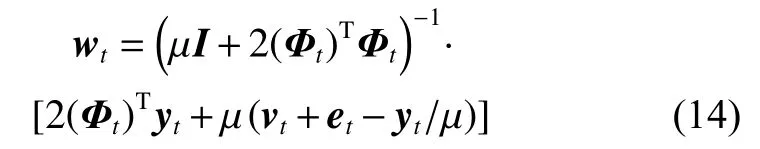
因此，可以進一步得到W的解：

2) 固定W、E、Y，式(12)轉化為目標函數：

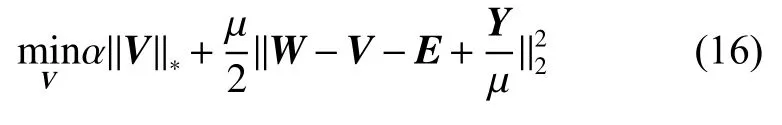
使用奇異值閾值算子[22]求解式(16)的低秩問題，V的最優解可以寫成如下形式：

3) 固定W、V、Y，式(11)變成如下目標函數：

式(18)等同于求解如下問題：

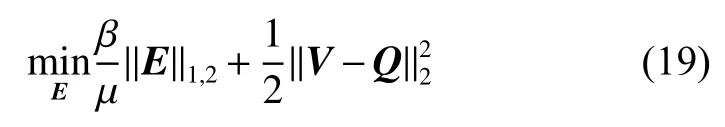
其中Q=W?V+Y/μ，可以使用文獻[23] 中的方法求解式(19)的最優化問題，得到E的最優解。

4) 更新拉格朗日乘子矩陣Y和正則化參數 μ：

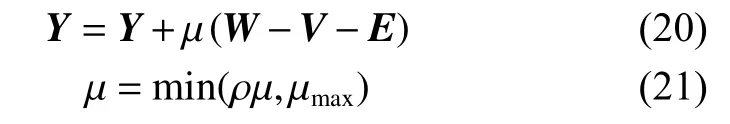
式中：ρ 是一個大于1 的正數。

最終，本文提出多任務TSK 模糊系統建模方法具體描述如下：

算法MTTSKFS-CS

輸入多任務數據集X1,X2,···,XT和對應的標簽y1,y2,···,yT；模糊規則數量M；正則化參數 α,β,μ ；可調節參數h；正整數 ρ>1，μmax=103；

輸出多任務的模糊前件和多任務后件參數聯合矩陣。

訓練過程

1) 生成模糊字典：首先對全部任務的樣本使用FCM 聚類，獲得M個聚類中心。然后計算每個樣本的模糊隸屬度，生成每個任務的模糊字典。

2) 聯合學習多任務的后件參數：求解式(12)，得到W、V、E最優解：

①初始化:設定W是一個隨機矩陣，V=W，E=W?V。拉格朗日乘子矩陣

②當式(12)不收斂

3) 輸出多任務的模糊前件和多任務后件參數聯合矩陣。

4 結果與分析

4.1 實驗設置

為了驗證本文提出的多任務建模方法的有效性，在多個真實數據集上進行泛化性能實驗。實驗中用到的數據集包含2 種類型：一種是相同輸入不同輸出的SIDO 數據集，將數據集的每一個輸出作為一個回歸任務構成一個多任務數據集，數據集的多個任務共享同一個輸入數據，但每個任務擁有不同的輸入空間到輸出空間的映射函數；另一種是不同輸入不同輸出的DIDO 數據集，同樣將每一個輸出作為一個回歸任務，每個任務擁有不同的輸入數據和不同的輸入空間到輸出空間的映射函數。

本節選擇的Slump、Parkinsons Telemonitoring、Winequality、House 數據集來自UCI Machine Learning Repository 數據集網站。Slump 數據集用來模擬混凝土的坍落度，涉及到坍落度、流動性和抗壓強度3 個輸出，是一個SIDO 數據集。Parkinsons Telemonitoring 數據集由來自42 名早期帕金森氏癥患者的生物醫學聲音測量組成，用來測量motor 和total UPDRS scores，也是一個SIDO 數據集。Winequality 數據集是一個利用基于理化測試數據來劃分葡萄酒質量等級的數據集，包括紅葡萄酒和白葡萄酒兩個子集，本節分別將每個子集視為一個任務，這是一個DIDO 數據集。House 數據集被用于波士頓房價預測，在本節根據特征變量“RAD”的值將數據集劃分為(Task 1:RAD<5;Task 2:5<=RAD <7.5;Task 3:RAD>=7.5)3 個子集，作為一個DIDO 數據集。Multivalued (MV) Data Modeling 數據集可以從KEEL Datasets Repository 獲得，是一個具有特征間依賴關系的人工數據集，本節中根據第8 個特征變量可以將數據集劃分為兩個任務，作為DIDO 數據集。表1 中列出來了上述所選用的數據集的特征維數、樣本數量等具體細節。

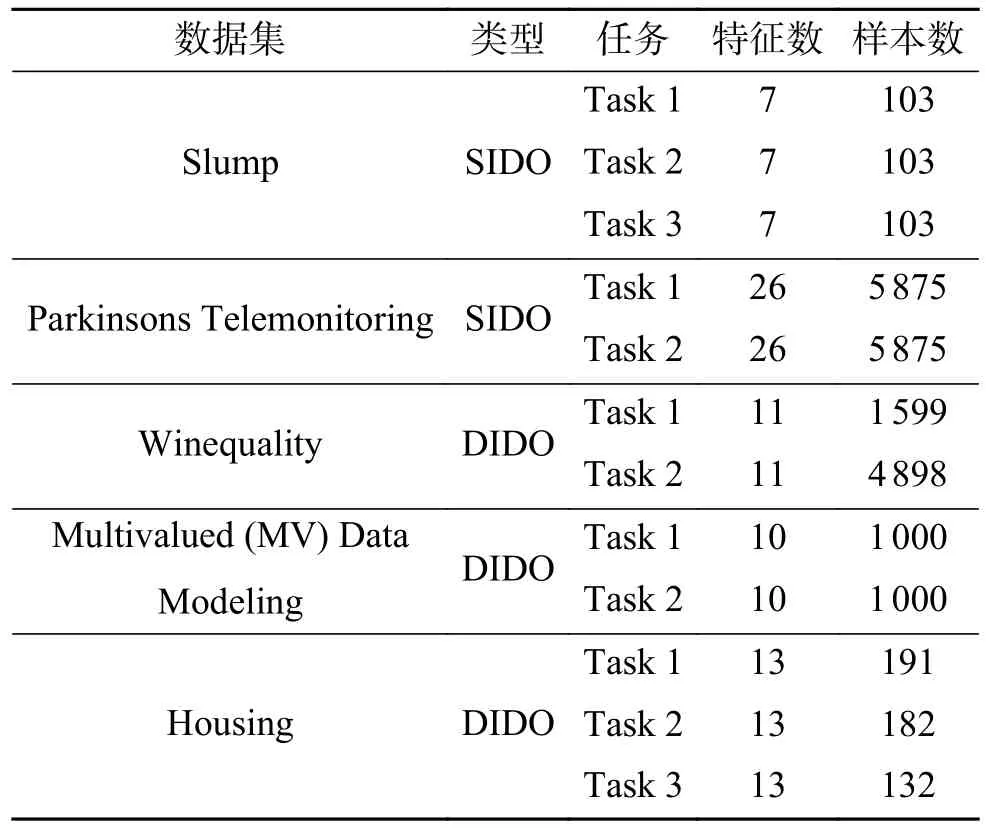
表1 多任務數據集的詳細信息Table 1 Details of the multitask datasets

我們在實驗中比較了幾種經典的回歸算法，包括多任務和單任務回歸算法。算法中涉及到的參數的設置通過5 折交叉驗證來進行尋優，這些算法的詳細介紹以及參數的尋優范圍如表2 所示。

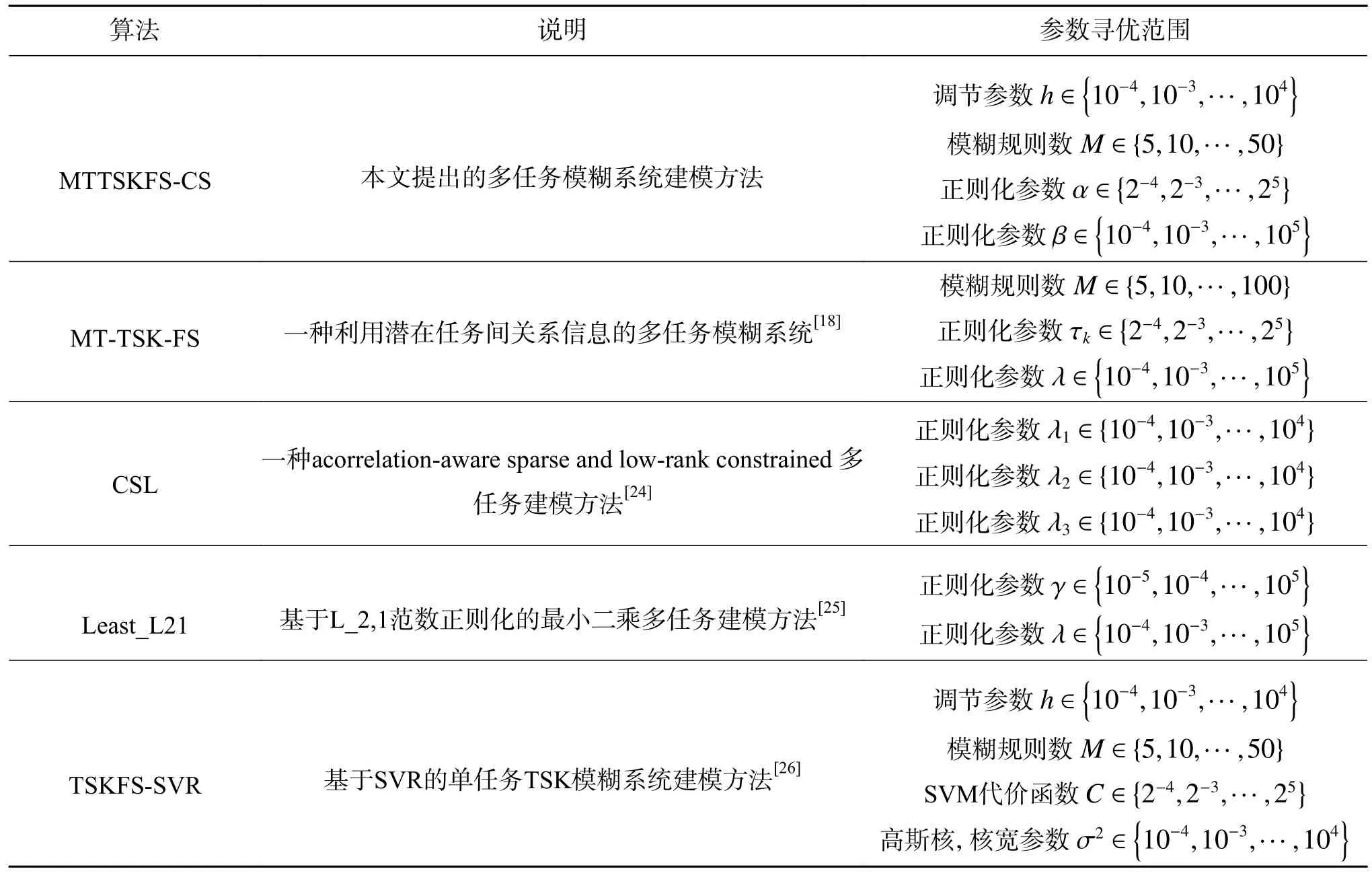
表2 實驗中各算法參數的詳細設置Table 2 Detailed settings of all algorithm’s parameters

本文選用RRSE 來評價各對比算法的泛化性能，定義如下：

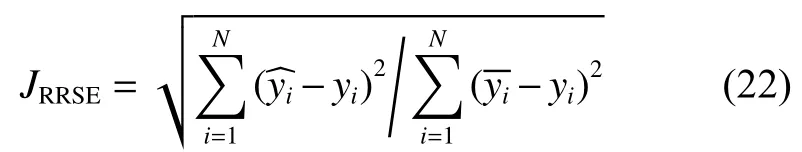
4.2 泛化性能實驗

我們分別在每個數據集上驗證了MTTSKFSCS 及對比算法。

分別計算各模型在每個數據集的每個子任務上的泛化性能，其中“Average”表示算法在每個數據集的所有任務中的平均表現。若算法為單任務算法時，分別對每個子任務進行建模，來評價算法性能。本文提出的MTTSKFS-CS 建模方法與對比方法在真實數據集上的實驗結果如表3 所示。

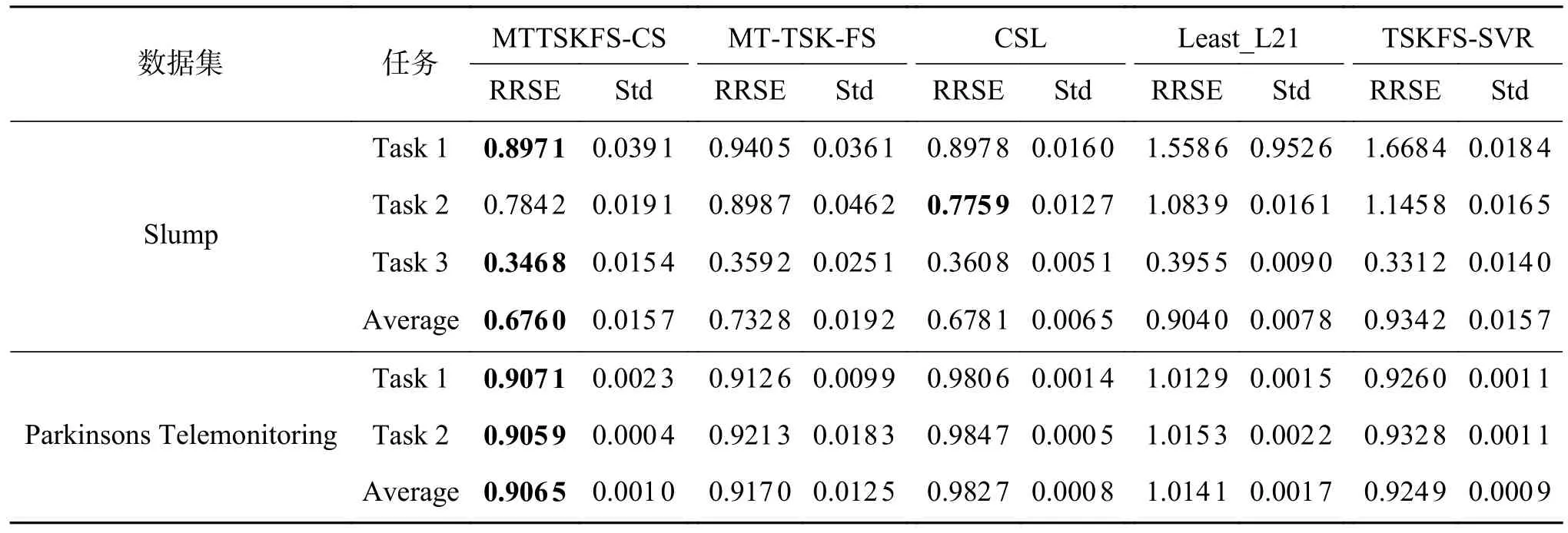
表3 所有算法在各數據集上的泛化性能比較Table 3 Comparison of generalization performance of all algorithms on datasets

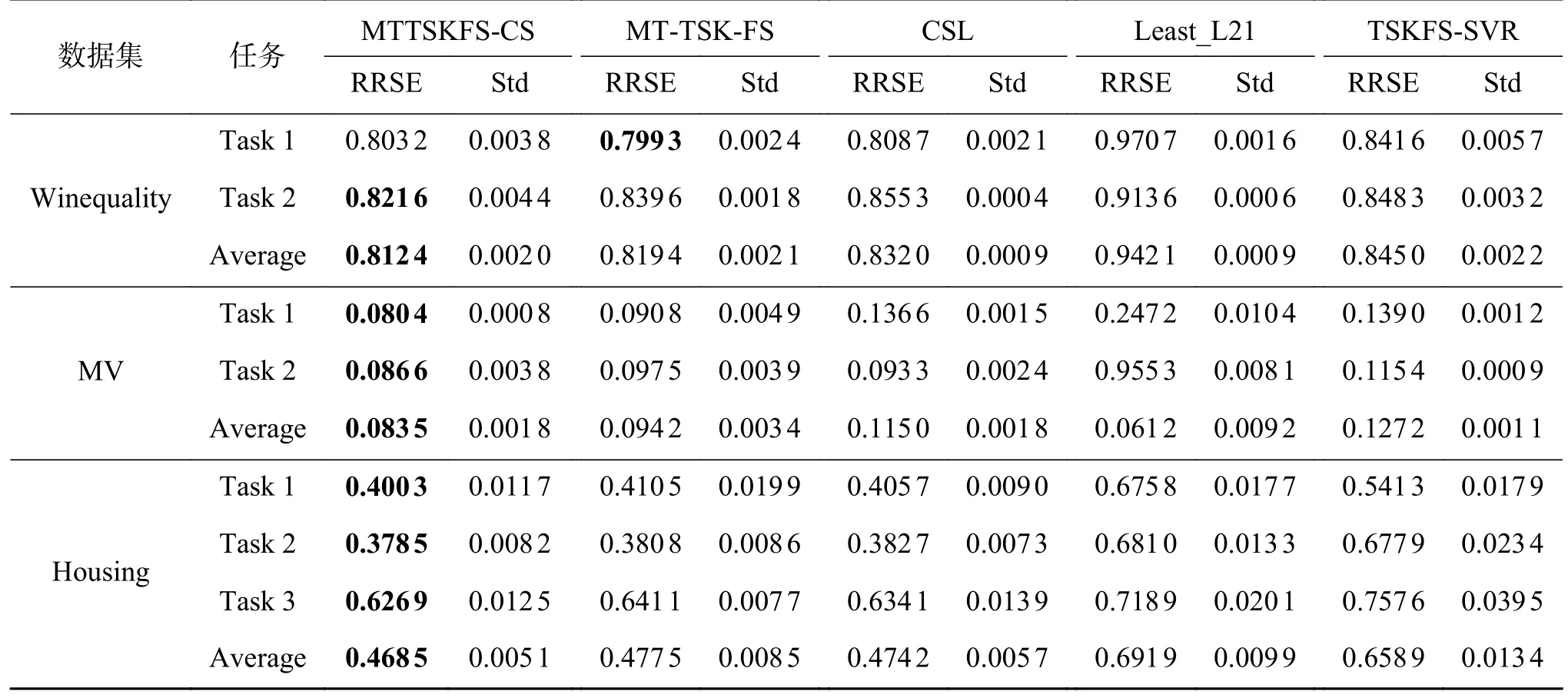
續表 3

4.3 后件參數劃分的可視化分析

為了進一步說明本文提出的對于后件參數矩陣的低秩和稀疏劃分的重要作用，我們將模型在Parkinsons Telemonitoring 數據集上訓練出的后件參數W、V、E進 行可視化。圖2 展示了后件參數的可視化結果，從中可以看到，訓練出的參數結果，基本符合圖1 中的假設，W被劃分為了低秩部分V和稀疏部分E。

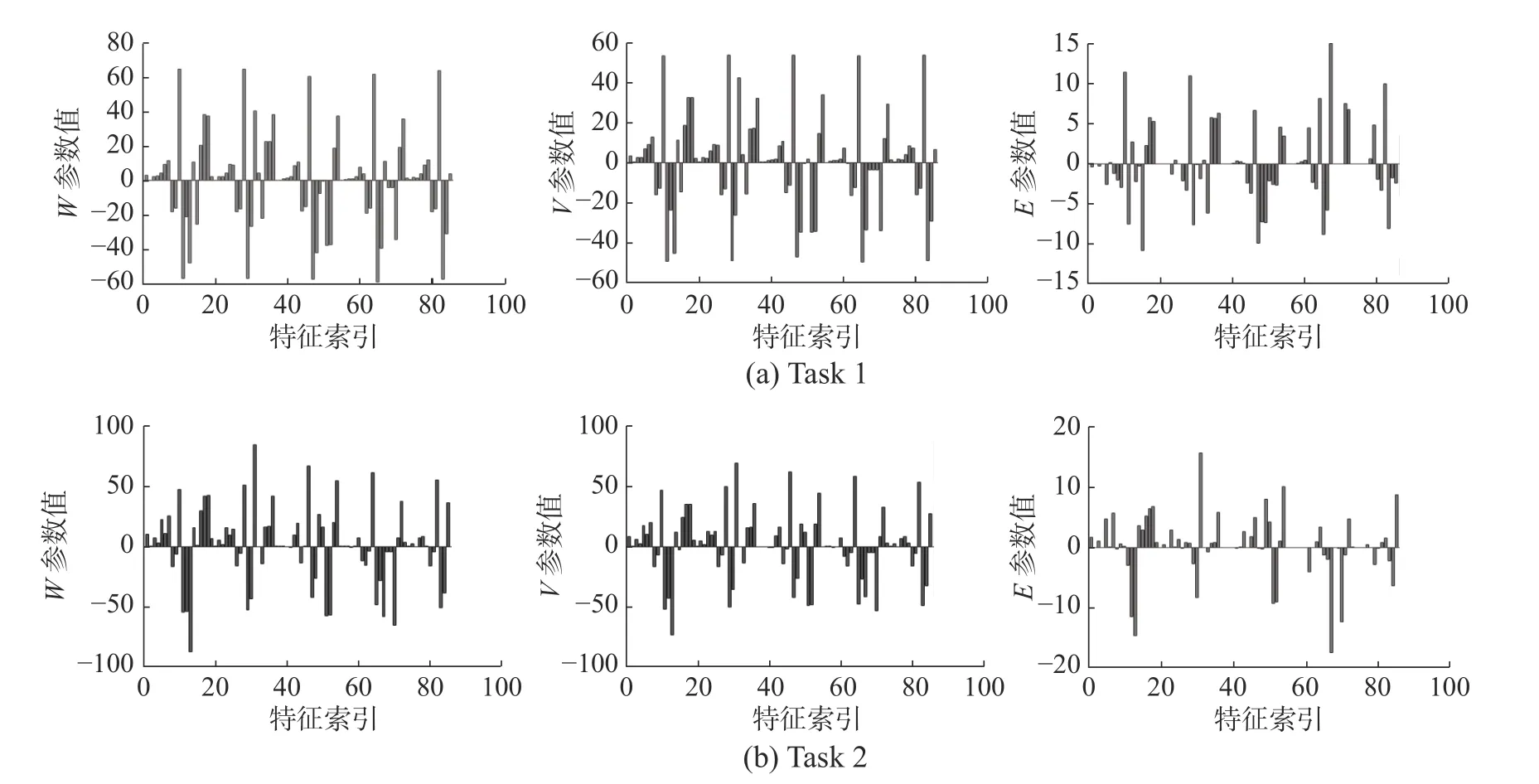
圖2 W、V、E 的可視化結果Fig.2 Visualization ofW,V,E

4.4 算法收斂性分析

為了進一步研究本文提出的MTTSKFSCS 建模方法的收斂性，我們選取了Multivalued(MV) Data Modeling、Parkinsons Telemonitoring 和House 3 個數據集，通過交叉驗證尋優得到最優參數，并在最優參數的基礎上進行收斂性實驗。算法在3 個數據集上的收斂曲線如圖3 所示。從收斂曲線中可以看到，算法在前期可以快速收斂，并迅速進入穩定狀態。實驗結果說明，本文第3 節提出的優化方法具有良好的收斂性能，能夠真正達到模型最優化的目的，從而使模型獲得較高的實用性。

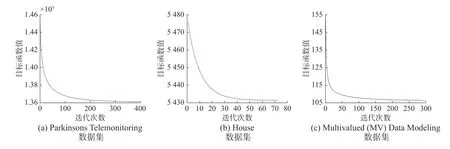
圖3 MTTSKFS-CS 方法的收斂曲線Fig.3 Convergence curve of MTTSKFS-CS algorithm

4.5 實驗結果分析

表3 的實驗結果證明MTTSKFS-CS 方法在大多數任務上獲得了比對比算法更好的性能表現。與單任務方法相比，多任務建模方法明顯提升了每個任務的預測表現，擁有更好的泛化性能。與多任務算法的對比結果說明，本文提出的方法在利用了多任務之間的的共享信息的同時有效利用了單個任務自身的特有信息，從而獲得了更好的表現。對于圖2 的可視化結果，我們可以看到，后件參數聯合矩陣W被劃分為了低秩部分V和稀疏部分E，實現了本文提出的模型設想，也間接驗證了MTTSKFS-CS 模型的有效性。

5 結束語

本文提出了一種新型多任務模糊系統建模方法，首先使用模糊聚類方法獲得多任務的模糊前件，然后通過合理劃分后件參數聯合矩陣為共享參數矩陣和特有參數矩陣，同時兼顧多任務之間的共享信息和各任務的特有信息。最后通過ALM 方法求解最優化問題，獲得模型的最優解。在多個真實多任務數據集上的實驗結果說明了，本文提出的MTTSKFS-CS 建模方法能夠有效解決傳統多任務模型只著重于多任務共享信息的問題。在今后的工作中，如何更好地在建模中平衡共享信息和特有信息將是我們研究的重點。