高等數學教學方法改革路徑探索與實踐

許曰才

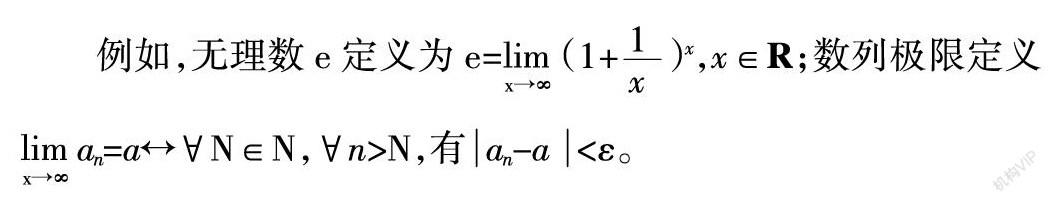
[摘? ? ? ? ? ?要]? 高等數學是一門非常重要的基礎性課程，內容豐富，理論嚴謹。在具體教學中，要加強與中學數學的聯系、注意數學思想方法的總結和滲透、提供易于記憶的結論表達式、善于運用數學符號語言、充分利用習題課、培養學生“用數學”思維、拓展“互聯網+”新思路，通過創新改革教學方法，提高學生的學習興趣和數學學習能力。

[關? ? 鍵? ?詞]? 高等數學;教學方法;改革路徑

[中圖分類號]? G642? ? ? ? ? ? ? ? ? ?[文獻標志碼]? A? ? ? ? ? ? ? ? ? ? ? [文章編號]? 2096-0603（2021）28-0220-02

一、高等數學教學方法改革的必要性分析

高等數學是普通高等院校開設的一門重要的基礎課程。高等數學不僅為學生學好數學和其他課程打下堅實的理論知識，還能為后續專業課程的學習提供基礎和保障。因此，學習高等數學具有十分重要的意義與價值。高等數學作為一門嚴謹性、邏輯性和抽象性較強的學科，涉及諸多公理化體系，主要包括推理邏輯以及定義、定理，所以存在一定的學習難度。教學中經常有學生存在內容抽象聽不懂、不會做題、難以理解等學習困難，甚至出現厭學情緒。教師如何解決上述學習問題，讓學生對高等數學教學產生興趣，進而接受并樂于學習高等數學是值得研究和思考的問題。筆者在教學中摸索了一些高等數學的教學改革方法，現總結如下。

二、高等數學教學方法的改革路徑

（一）加強與中學數學的聯系，提高學生的學習興趣

在教學中，要充分挖掘高等數學與中學數學有關的內容和方法，并加強其應用，增強學生學習高等數學的積極性。

1.進行適當的補充，做好初等數學與高等數學的銜接

高等數學和中學數學有不少脫節的地方，首先是數學知識上的脫節，高等數學中有些內容涉及某些中學數學的知識，中學沒講或沒講透等，而高等數學一帶而過，教師認為已講未予重視，結果造成某些知識處于兩不管狀態。如中學里講過各種不等式，但卻沒有講放大法，而極限內容經常用放大法;其次是邏輯與思維方法上的脫節，如不少學生為什么掌握不好極限概念，其主要原因是極限概念中使用了量詞（任給、存在），而高等數學與中學數學都沒有講量詞（屬邏輯學內容）的有關知識。這樣學生學習有困難，甚至產生畏難情緒。在教學中根據需要補充適當的內容，使學生順利地過渡到高等數學的學習。

2.注意高等數學對中學數學的指導作用

高等數學是中學數學的繼續和深入，對中學數學具有指導作用，突出表現在以下兩點：一是為中學數學的有關內容提供了理論依據，如高中立體幾何課本中介紹了祖原理，由于初等數學的局限性，課本上沒有給出證明，而利用定積分就可以證明其正確性，又如中學生用的數學用表是怎樣制造的，學了函數的冪級數展開的知識就容易回答這個問題了;二是為中學數學有關內容提供了簡便計算和證明的有力工具。如中學數學中求極值、某些不等式證明等，用初等方法很麻煩，而用導數來解決非常簡單。

（二）注意數學思想方法的總結與滲透，教給學生“點金術”

學生厭學高等數學的原因之一是學了知識以后遇到問題不會解決，缺乏分析問題、解決問題的能力。定理的證明及習題的求解中，有很多思想方法，如累次法、類比法、數形結合、分段處理法等，在教學中要善于總結或讓學生總結，教給學生“點金術”，這樣學生在做習題時就不會感到束手無策、不知所措。

例如，通過二元函數的微分中值定理及泰勒公式的證明可總結出研究二元函數f（x，y）在兩點A（x1，y1）與B（x2，y2）上的函數值之差Δ=f（x1，y1）-f（x2，y2）的性質的方法——累次法，即將多化單，其具體方法：

（三）提供易于記憶的結論表達式

高等數學的內容很多，學生在有限的課堂上學會那么多的知識存在一定的難度，因此，教師要將所學內容進行梳理，“梳成一條辮子”或提供一些易于理解和掌握的結論，幫助學生理解，便于學生掌握。

求多元復合函數的偏導數，用樹形圖講解效果好。樹形圖把函數、中間變量及自變量放在一起，復合關系清楚，求導時不易出錯。

樹形圖：

（四）善于運用數學符號語言進行教學

普通思維靠詞語，表述繁雜冗長，歧義橫生;數學思維靠符號語言，簡明準確，自成體系。數學符號繁多，含義豐富深刻。隨著數學的不斷發展，數學內容越來越抽象，然而不同符號很容易把數學內容表述清楚，于是數學符號的使用尤為重要，使用也更加廣泛。數學符號是簡捷化了的數學語言，它使數學語言變得精練、準確。正確使用數學符號，有利于數學思維和數學交流。在教學中，教師必須熟練而正確地使用各種數學符號，才能準確地表達定理和公式，流暢地進行數學交流，科學地傳授數學知識，易于學生記憶和理解的同時提高教學效果。

（五）充分運用習題課教學

數學習題課的教學是數學整體教學的組成部分，是課堂教學的基本組織形式。在以學生為主體的教學思想指導下，其越來越被重視。具體而言，習題課是在教師的講解、指導下，學生獨立或經過討論完成練習的課型。加強習題課的組織和教學，及時捕捉教學信息和反饋，一方面可以進一步幫助學生理解和鞏固數學基礎知識和基本方法，從而培養學生的分析能力、運算能力和推理論證能力;另一方面可以更加了解學生，從而改革教學方法，提高教學質量。