維數約化的弱耦合KP-Boussinesq方程的lump解和有理解

劉 袁,汪一航

（寧波大學 數學與統計學院,浙江 寧波 315211）

非線性演化方程描述了非線性現象,具有廣泛的應用.非線性演化方程的精確解在非線性科學中起著至關重要的作用[1-2].lump 解是一種特殊的有理解,它在空間的各個方向都是局域的[3-4].基于構造平方函數[5-7]和長波極限的方法[8-10],諸多方程都被發現存在lump 解.

(3+1)維的廣義KP-Boussinesq 方程[11]為

相當于把utt的項添加到廣義KP 方程中,u=u(x,y,z,t)是可微函數.通過變量變換

可得式(1)的Hirota 雙線性形式,即

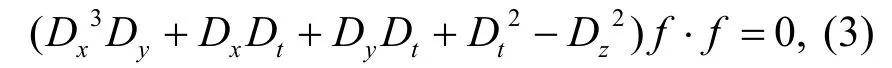
式中:f=f(x,y,z,t)為實輔助函數;D為Hirota雙線性微分算子.利用極大交換子代數中取值的Zm-KP 方程族結構[12-13],得到弱耦合KP-Boussinesq方程:

式中,v=v(x,y,z,t)是可微函數.

1 lump 解和有理解

1.1 lump 解

對于z=y的情況,式(4)可簡化為

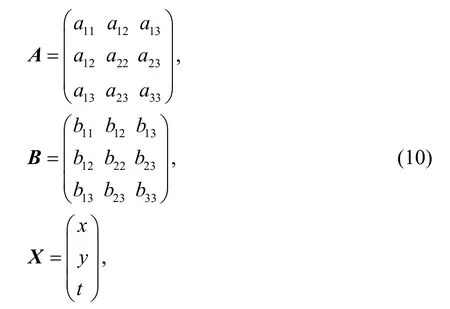
A和B為對稱矩陣,A和B的元素及c1、c2均為實變量.

將式(9)代入式(7),求解方程得到各參數的約束方程

為保證解u為lump 解,矩陣A和參數c1必須滿足以下約束:

(i)矩陣A是一個半正定矩陣;

條件(i)和(ii)保證f是一個恒大于0 的函數.條件(iii)保證f在任意時刻只有一個最小值.

在式(12)中有自由參數a22、a23、a33和c1.對各參數取值如下:

圖1 t=0 時lump 解u 的特征

圖2 t=0 時lump 解v 的特征

1.2 有理解

本節主要研究方程(4)的另一種有理解,它表現出不同于lump 解的性質.

將式(9)代入式(7)可解得如下約束方程:

上式包含3 個自由參數b22、b23和b33,令參數值為

輔助函數g的解析表達式為

那么在變量變換(6)下可得vr:

上述vr為方程(5)的有理解,圖3 所示為有理解vr在不同時刻的動力演化.

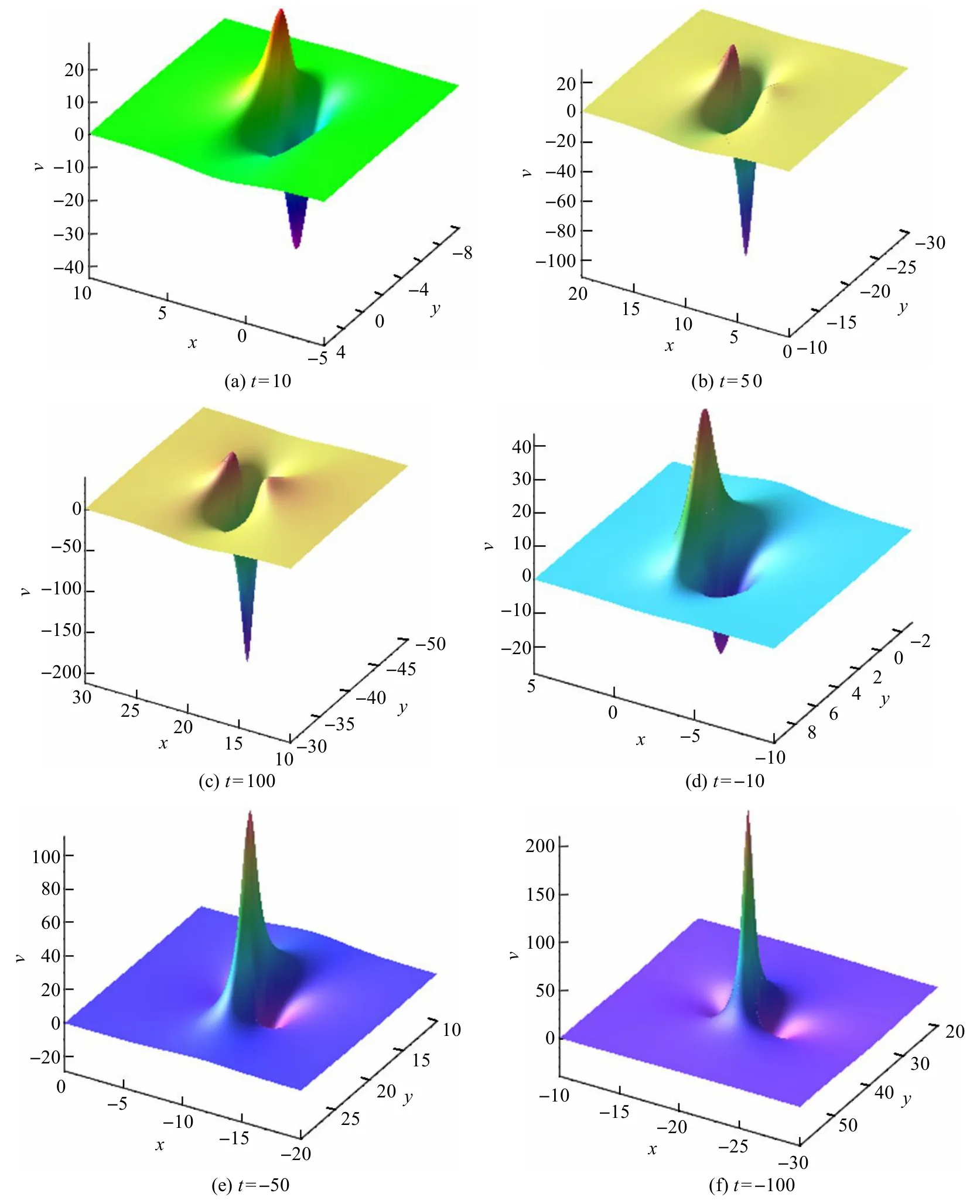
圖3 有理解 v r在不同t 下的動力演化

分析有理解vr,其表現出不同于lump 解的性質.首先,vr是奇函數,即滿足vr(x,y,t)+vr(-x,-y,-t)=0.如果能計算出波峰在t﹥ 0時的軌跡,那么可知任何t下的波峰位置.vr的偏導數反映了解的極值的性質,通過計算vr,x=0和vr,y=0不能直接解出有理解的極值.為了分析解的波峰和軌跡變化,需要采用數值方法來研究其性質.

表1 描述了t取不同值時有理解vr的波峰變化,其中h為峰值高度,|vr,x|和|vr,y|的數值越小,計算的波峰位置越精確.從圖3 可以看出,隨著時間的增加,波峰高度逐漸減小.當t﹤ 0時,波峰高度為正;當t﹥ 0時,波峰高度為負.

根據前面的描述,對表1 中的數據進行非線性擬合.

表1 有理解 vr 的波峰位置和高度

對于t﹥ 0,波峰的運動軌跡近似符合下式:

根據奇函數的性質,在t﹤ 0處波峰的軌跡為

波峰的高度h為

由式(23)可知,隨著時間的增加,波峰的運動過程近似為勻速線性運動.此外,任何單位時間所產生的高度變化值大約為2.為驗證式(21)和式(22)能否準確表示出波峰的位置和高度,另取不同的t值,可得相應的波峰坐標和高度,見表2.其中|vr,x|和|vr,y|略有增加,這是因為當|t|越大,波峰越尖銳,高度h的誤差略有增加,但這仍是有效計算出波峰高度的一種方法.

表2 有理解 vr 的估計

2 結語

在本研究中,利用Zm-KP 方程族構造了一個新的弱耦合廣義KP-Boussinesq 方程.基于Hirota雙線性方法和符號計算研究了其維數約化情形的有理解問題.通過假設半正定的對稱矩陣形式的輔助函數,限制參數之間的關系,得到了lump 解和有理解,并討論了lump 解的動力學性質.然后發現了一種不同于lump 解的有理解,并分析了其動力學性質.由數值分析給出了有理解的波高和極值點的運動軌跡,并通過相應的圖表來說明其運動規律.希望本文所描述的新結果能夠對其他非線性模型的應用有所幫助.