基于EEMD-RVM的土石壩滲流量時間序列預測模型

劉永濤，鄭東健，孫雪蓮，曹立林

(1.河海大學水利水電學院，江蘇 南京 210098； 2.河海大學水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210098；3.中國電力工程顧問集團華東電力設計院有限公司，上海 200063； 4.江蘇省連云港市通榆河北延送水工程管理處，江蘇 連云港 222023)

土石壩由于其經濟性、施工技術簡便及對地形地質適應性強等優勢在壩工領域應用最廣泛。在國際大壩委員會的3次潰壩事故調查報告中[1]，土石壩的潰壩數量占大壩潰壩總數的70%，其中約25%土石壩的潰決是由壩體滲透破壞導致。為保證運行期土石壩的滲流安全，需結合監測資料對土石壩的滲流進行監控。運行期土石壩滲流監測內容一般為壩后滲流量與壩內滲壓水頭，其中滲流量是土石壩運行性態的直接表征[2]。因此，研究土石壩滲流量的變化趨勢對準確評價大壩安全具有重要意義。大型土石壩工程由于監測資料詳實、可靠，因此很多算法可以較好地實現環境量與滲流量之間的映射關系，并且滲流量的預測精度較高，能滿足工程應用要求[3-4]。而對于占我國大壩總數90%[5]以上的中小型土石壩，一般監測資料會存在不同程度的缺測，特別是環境量。另一方面，由于規律性不強的降雨、變化的水位、壩體的時效變形等因素對滲流量變化影響較大，因此土石壩滲流的監測數據一般具有非線性及非平穩性，所以在不考慮環境量的情況下研究滲流量時間序列并準確預測比較困難。綜上，在不直接考慮大壩環境量對滲流的影響前提下，為了更簡便高效地進行中小型土石壩滲流量預測，以滲流量時間序列作為研究對象十分必要。

目前，在缺失環境量的情況下，為解決土石壩滲流量預測中的過擬合和結果不唯一等問題，一些學者在滲流量預測中引入了不同的學習算法[6-7]。這些算法，無論是傳統算法還是智能優化算法都存在諸多問題[8]，如參數初始值對預測結果的準確性影響較大、算法的魯棒性總體較差、算法迭代過于復雜且收斂緩慢、預測結果容易陷入局部最優且總體精度較低，所以滲流量時間序列的預測算法在理論研究和應用中均有待提高。為解決智能算法在非平穩時間序列的上述難題，Huang等[9]提出了經驗模態分解(empirical mode decomposition，EMD)算法，但EMD存在端點效應和模態混疊程度高的問題；針對EMD存在的問題，Wu等[10]對EMD進行改進，提出了集合經驗模態分解(ensemble empirical mode decomposition，EEMD)算法。目前，EEMD算法已應用于環境、水文、醫學、地質等多個行業[11-13]，但將其應用到土石壩滲流量預測中的研究甚少。

Tipping[14]建立的相關向量機理論(RVM)模型不僅解決了支持向量機(SVM)模型結構稀疏度不高的問題，還簡化了核函數的計算程序，提高了計算效率。高杰等[15]給出了基于RVM的邊坡可靠度計算方法，解決了極限狀態函數無法顯式表達、難以求解導數的問題，并且計算速度快、精度高；平善明等[16]通過RVM模型預測了短期風速，并較好地解決了由于間歇性和不穩定性導致風速擬合預測低的問題。

綜上，EEMD算法可以較好地解決大壩滲流監測值非平穩性所帶來的過擬合問題，RVM算法可以在大壩滲流值的訓練擬合和預測過程中提高算法收斂速率、預測精度以及模型的健壯性。因此，筆者運用EEMD算法對大壩滲流監測序列進行模態分解，結合高斯核函數的RVM模型對分解分量進行擬合訓練，構建基于EEMD-RVM土石壩滲流量時間序列的預測模型，在不考慮環境變量的前提下，以期提高土石壩滲流量預測的可靠性和精度。

1 土石壩滲流量預測模型

1.1 EEMD原理

在原始時間序列中多次加入足夠多的不同白噪聲，再將新的時間序列進行多次EMD分解得到多組本征模態函數；然后根據白噪聲均值為零的特點對各組本征模態函數分量作平均，可得到EEMD分解的IMF分量I和剩余量R[17]。過程如下：

首先，把高斯白噪聲M次加入原始時間序列得時間序列：

xi(t)=x(t)+ni(t) (i=1,2,…,M)

(1)

式中：x(t)為原始時間序列；xi(t)為第i次添加白噪聲的時間序列；ni(t)為等長度白噪聲信號。

然后，利用EMD算法分解新的時間序列，可得本征模態函數Ci,j(t)及一個剩余項ri(t)：

(2)

式中：Ci,j(t)為第i次添加白噪聲EMD分解所得到的第j個本征模態函數分量；ri(t)為剩余項；J為IMF分量的個數。

最后，利用互不相關的隨機序列之間均值為零的特性，將M組Ci,j(t)分量及剩余項ri(t)求算術平均得到最終的IMF分量I及剩余量R(t)。

(3)

(4)

式中：Ij(t)為EEMD最終分解分量；R(t)為最終剩余量。

1.2 RVM模型原理

tn=u(yn;ω)+εn

(5)

其中ω=(ω0,ω1,…,ωn)T

式中：yn為輸入向量值;tn為輸出目標值；ω為權重向量；εn為零均值的高斯噪聲且相互獨立，方差為σ2；N為樣本數；K(y,yn)為核函數。

設tn為獨立分布，數據序列完整概率為

(6)

其中t=(t1,t2,…,tN)T

Φ=(φ(y1),φ(y2),…,φ(yN))

φ(yn)=(1,K(yn,y1),K(yn,y2),…,K(yn,yN))T

當訓練序列中的參數增多時，σ2和ω的最大似然估計會出現過擬合現象，從而在預測過程中容易出現訓練模型中的控制參數溢出現象。為避免發生上述現象，本文結合SVM原理及Bayesian先驗特點，對一些參數附加約束條件[18]，以降低擬合及預測過程中的誤差，提高模型精度。因此對權重ω賦予一個均值為零的高斯分布：

(7)

式中:α為超參數，服從Gamma先驗分布。

由Bayesian知識和先驗分布p(ω,α,σ2)得后驗分布ω：

(8)

其中Σ=(σ-2ΦTΦ+A)-1μ=σ-2ΣΦTt

A=diag(α0,α1,…,αN)S=N+1

式中：Σ為后驗協方差；μ為后驗均值。

對式(8)的ω積分，得到由α、σ2表示的邊緣分布為

其中Ψ=σ2I+ΦA-1ΦT

式中：Ψ為中間變量；I為單位向量。

最大化求解超參數邊緣分布，通過迭代計算α和σ2，可得優化參數：

(10)

(11)

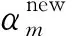
t*=μTφ(y*)

(12)

通過快速序列稀疏Bayesian算法計算超參數和噪聲方差，則模型高斯核函數為[19]

K(y,yn)=exp(-g‖y-yn‖2)

(13)

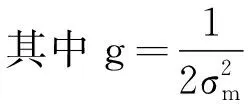
式中：σm為函數的寬度參數。

1.3 土石壩滲流量預測模型構建

在不考慮環境量的前提下，本文綜合利用EEMD算法和RVM算法的優點和特性將其串聯，構建基于EEMD-RVM土石壩滲流量時間序列的預測模型。首先運用EEMD模型對土石壩滲流量監測序列進行模態分解，然后通過RVM模型對分解的各分量進行擬合訓練，再將預測時間t代入訓練好的分量函數得到分量預測值，最后將每個分量的預測結果相加求和則可得到滲流量預測結果。該模型具體實現過程如圖1所示。

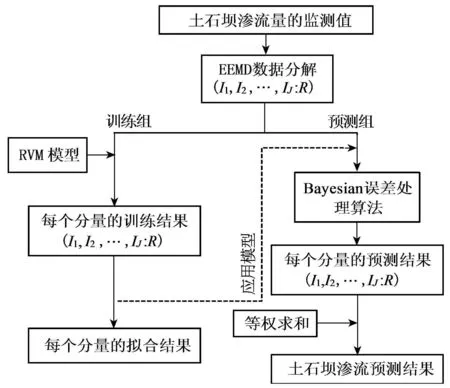
圖1 基于EEMD-RVM土石壩滲流量預測模型

2 算例驗證

2.1 EEMD分解滲流量時間序列

以某土石壩為例，該壩位于我國東南地區，最大壩高120.0 m，壩頂高程760.00 m，壩頂長度259.8 m，壩頂寬度9.0 m。壩址以上控制流域面積453 km2，水庫校核洪水位(洪水頻率0.05%)759.10 m，設計洪水位(洪水頻率1%)756.20 m，正常蓄水位755.00 m，總庫容2.65億 m3，為多年調節水庫。該壩滲流量采用量水堰人工測讀，監測頻率為一周一次，選取2015年1月7日至2017年8月31日的129個滲流量監測值作為計算訓練組；選取2017年9月15日至12月29日的15個滲流量監測值為預測組。訓練滲流量時間序列樣本的時間作為輸入值，相應的滲流量作為輸出值，基于EEMD-RVM建立土石壩滲流量的預測模型。

首先對滲流量監測數據進行平穩化處理，基于EEMD算法進行分解、重組。EEMD算法分解參數有2個：高斯白噪聲標準差S(一般為0.01～0.40)和添加白噪聲次數M(一般為50～200)。對于平穩性較好的滲流序列，S、M均可以取小點，具體取值由序列特征決定。

取2015年1月7日至2017年8月31日的滲流量監測數據為訓練組。在原始監測時間序列添加100組白噪聲序列，每組高斯白噪聲標準差S設為0.2進而可得I分量6個和剩余分量1個，分解結果如圖2所示。

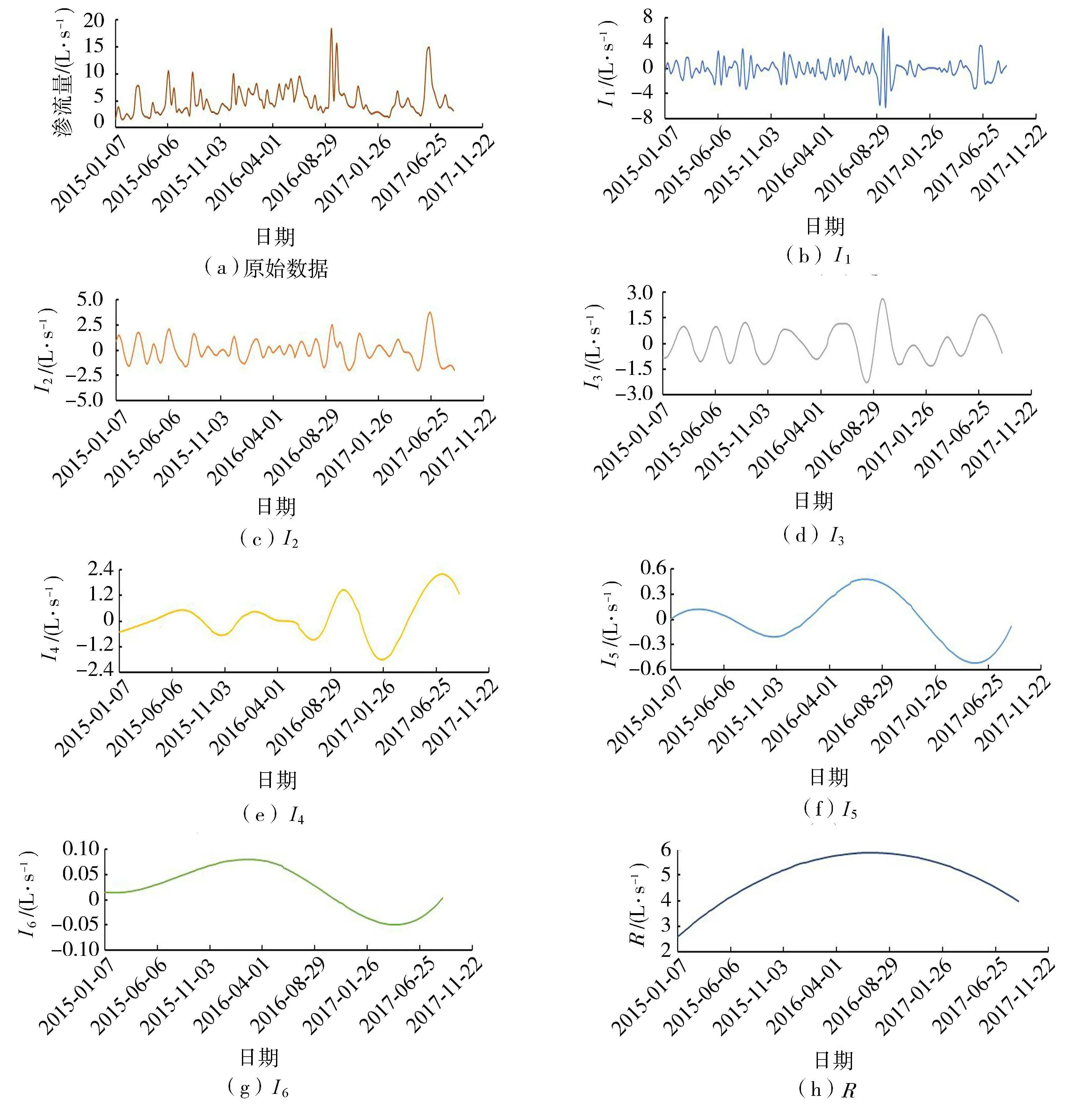
圖2 EEMD分解的IMF分量及R分量結果

2.2 RVM對各分量的訓練擬合

EEMD分解得到滲流量的分量后，采用RVM算法對分量進行訓練擬合。RVM算法相關參數參考前人研究成果[20]取定：慣性因子取值范圍0.3～0.8，核參數中g取值0.01～1.0，學習因子C1取值為1.2～2.5，學習因子C2取值為1.5～2.55，核函數的位置因子ν取值為0.01，速度因子γ取值為1.00。

通過RVM模型可擬合6個I分量及剩余分量R的函數，通過對比實測值與RVM模型擬合值得到擬合誤差，進而通過快速序列稀疏Bayesian算法對擬合結果進行誤差處理，然后對各個分量的擬合值求和得滲流量擬合值。該壩滲流量的擬合結果如圖3所示，擬合結果的判定系數為0.98，表明該模型的擬合精度高。

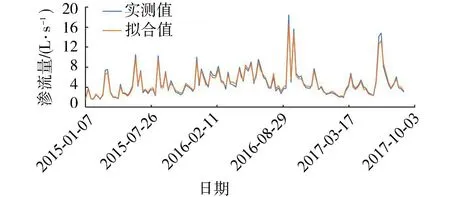
圖3 EEMD-RVM模型滲流量擬合過程線

2.3 滲流量預測結果及誤差分析

將預測集的2017年9月15日至12月29日的15個時間點代入已訓練好的各I分量及R分量的函數求得各分量值，再把各分量的值相加得到土石壩滲流量的最終預測結果。為分析該模型的精度，給出傳統的GA-BP模型以及RVM模型預測結果，各模型預測結果如圖4。3種模型滲流量預測值的相應平均殘差結果如圖5所示，其中EEMD-RVM模型、GA-BP模型與RVM模型3種模型的預測滲流量的平均絕對值殘差分別為0.222 L/s、0.674 L/s和0.653 L/s，平均相對誤差分別為14.9%、49.7%和48.8%。由此說明，EEMD-RVM模型可以大幅提高滲流量預測精度，并且對突跳值更敏感，整體預測結果更好，對環境量存在缺測的中小型土石壩水庫的滲流量預測提供了新方法。

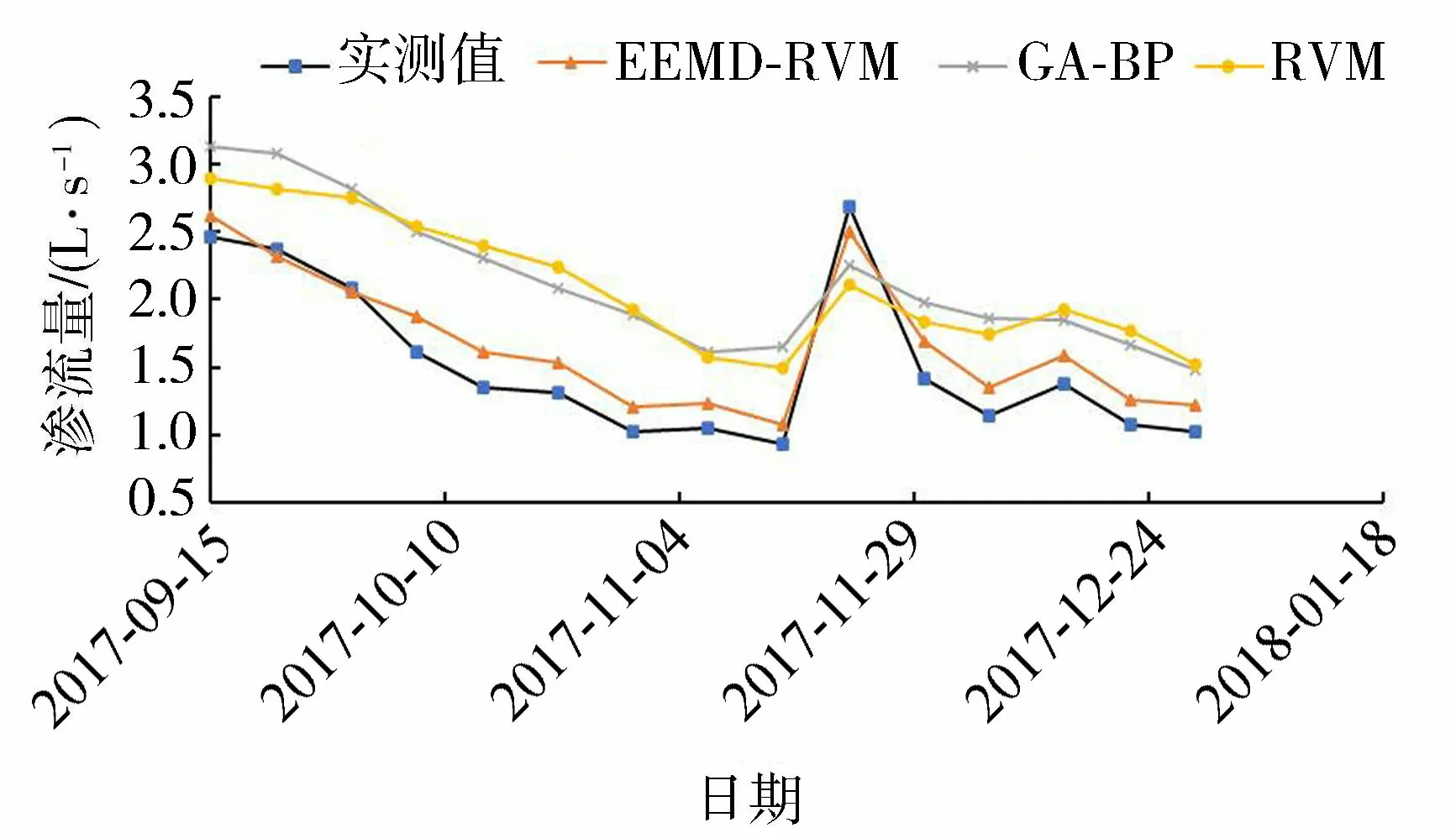
圖4 3種模型滲流量預測結果對比

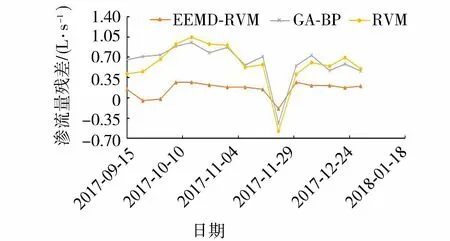
圖5 3種模型預測結果殘差對比

由實例計算可知EEMD-RVM滲流預測模型的精度和可靠性較高，為了增加該模型的適用性以及方便大壩管理人員的實際應用，對模型的樣本數和相關預測情況進行說明。

a.一般研究大壩滲流預測問題，在訓練過程中訓練集有大樣本和小樣本2種。本文模型研究的是大樣本情形。對于大樣本訓練，一般取一年以上，這樣可以較完整地捕捉到降雨、水位等年變化因素對滲流影響的規律特性。又由于大壩的滲流特性隨著運行時間的增加而漸變，所以如果訓練樣本過多，則不能較好地反映當前的大壩滲流情況。因此，建議本文模型的訓練樣本取1～2 a。對于小樣本，由于滲流實測資料較少，所以一般取所有測量值為研究對象。

b.對于預測時長的確定，時長并不是越長越好，因為時長越長必然帶來誤差增加，以至后期誤差較大的預測值不具有工程指導意義。在水工建筑物的預測研究中，一般取訓練集時長的10%～20%為預測集的時長。由于滲流的不穩定性，大壩的滲流預測比其他預測，如位移、應力的預測更難。所以為了提高滲流預測的精度，建議預測時長取訓練集時長的10%～15%。

c.在滲流實測過程中，不可避免會出現突跳值的情況。對于突跳值的預測，一直是研究的難題。一般突跳值有2種：突增和突減。其中滲流的突增往往對于大壩安全更不利，建議增加預測值的安全裕度以對工程管理提供可靠的支持。本文算例在預測過程中的2個突跳點(2017-11-22和2017-12-15)的預測相對誤差分別為7.06%和15.21%，對于該壩建議對突跳點的預測值增加5%～15%的安全裕度。由于每座大壩的滲流情況不同，可以對過去滲流情況進行訓練并比較預測值與實測值的誤差，分析出突跳點的預測誤差。根據預測誤差情況，可以調控預測結果和提高預測值的安全裕度以方便工作人員更好地管理和決策。

3 結 論

a.EEMD算法將滲流量時間序列分解處理為平穩子序列，可以有效地提高非平穩滲流監測數據的分析精度。

b.EEMD-RVM模型與RVM模型及GA-BP模型的結果對比可知：常規模型對滲流量時間序列的預測誤差較大，EEMD-RVM模型較大幅度地提高了預測精度，表明該模型在土石壩滲流量時間序列中具有較高的可靠性。

c.通過實例和驗證結果可得，EEMD-RVM模型在工程應用上可行，操作性較高，精度滿足要求。對于環境量監測缺失較為嚴重的中小型土石壩，特別是中小型病險壩，該模型可以快速進行滲流量預測研究，為提高中小型土石壩的滲流安全提供了新的途徑和方法。