固體顆粒粒徑對輸送泵葉輪磨損特性的影響①

張 勝，曹 騫，康 燦，丁可金，李長江

（1．國家泵類產品質量檢驗中心（山東），山東 淄博255209；2．江蘇大學能源與動力工程學院，江蘇 鎮江212013；3．中國船舶重工集團公司第七○四研究所，上海200031）

葉片泵是輸送固液兩相混合物的關鍵裝備，固體顆粒對葉片泵過流部件的磨蝕是輸送泵中的突出問題之一。顆粒與壁面發生碰撞和摩擦，造成輸送泵過流部件表面材料去除，泵效率和運行穩定性下降，嚴重時導致輸送泵停機和整個流程的中斷［1－2］。研究輸送泵內的固液兩相流動、顆粒運動規律及顆粒對泵過流部件的磨損具有重要意義。

隨著計算流體動力學（CFD）技術的發展，流動模擬的準確性不斷提高，其已成為泵內固液兩相流動研究的主要方法之一。基于對流動的模擬，考慮顆粒的運動及物理屬性，進而嘗試對顆粒對壁面的磨損進行模擬［3－5］，這是目前的研究熱點之一。

由于固液兩相流體輸送泵內顆粒運動非常復雜，并且受到顆粒物理性質（硬度、形狀、粒徑等）和顆粒群性質（濃度、粒徑分布等）的綜合影響，過流部件的磨損行為和影響因素難以準確描述，對于其中磨損機理的認識還不夠深入。以往研究中通常忽略顆粒之間的碰撞，得到的磨損規律與物理真實之間存在一定的差距。本文借助EDEM和ANSYS Fluent商用軟件，采用離散元方法（DEM）和CFD耦合的方法進行數值模擬，充分考慮顆粒之間、顆粒與液體之間的相互作用，模擬輸送泵內固液兩相流動，并使模擬更接近實際運行工況［6］。同時，獲得輸送泵過流部件的磨損特性，并考慮顆粒粒徑變化對磨損結果的影響，對比分析其中的規律，為輸送泵抗磨損設計及運行優化提供支撐。

1 輸送泵參數與幾何模型

選取某固液兩相流體輸送泵為模型泵，其基本設計參數及葉輪主要幾何參數如表1所示。

表1 輸送泵設計參數及葉輪幾何參數

圖1為輸送泵結構示意圖。該泵為臥式單級單吸離心泵，固液兩相介質自水平方向吸入。葉片為圓柱形葉片，在葉片進口略扭曲以提高流動質量。葉片間流道相對于普通離心泵葉片流道寬敞，以提高固液兩相流體的通過性。葉片數為8，其中包含4個長葉片和4個短葉片，短葉片靠近長葉片工作面布置。葉片后蓋板不設背葉片，采用開槽結構。

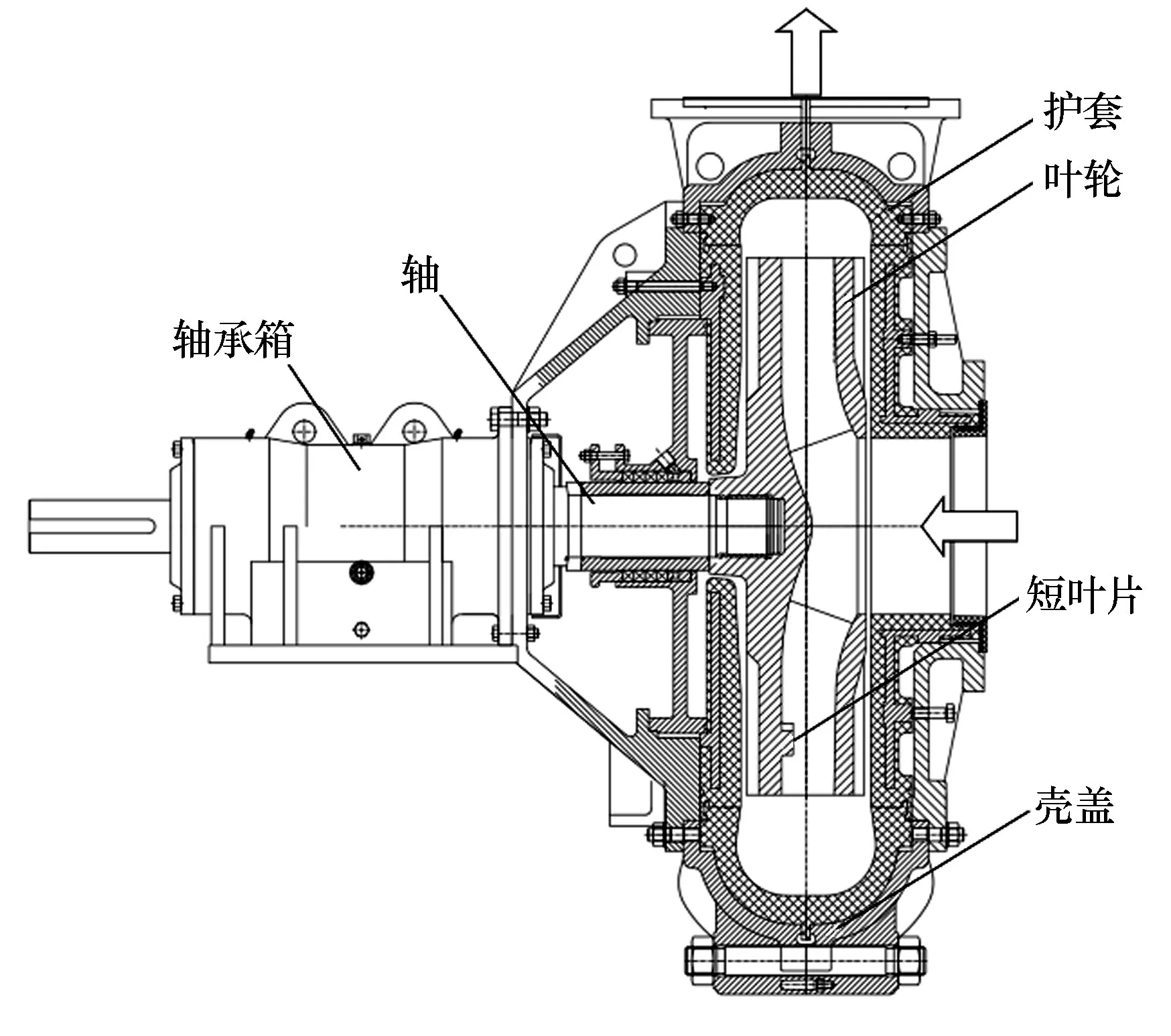
圖1 輸送泵結構示意圖

采用Siemens NX軟件對該輸送泵過流部件進行三維建模，考慮其中圓角、過渡等小尺度幾何特征。經過布爾運算后獲得流動充滿的空間模型，即水體模型，整個水體模型由吸入段、葉輪區域、壓出室域和出口段構成，如圖2所示。

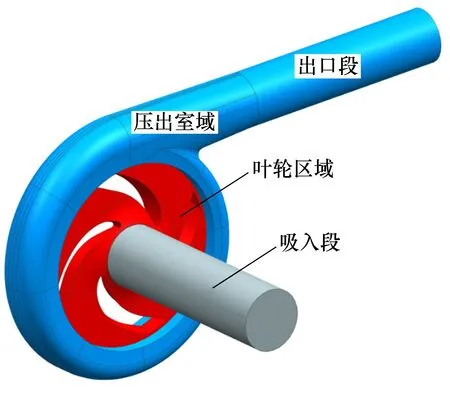
圖2 計算域水體幾何模型

2 數值模擬方法

2．1 基本假設

為探究不同粒徑的固體顆粒磨損輸送泵過流部件的規律，假設清水為連續相，為不可壓縮流體，固相顆粒為離散項，每相的物理特性均為常數；顆粒為直徑均勻的球形顆粒，每個顆粒的物理性質均相同，且不考慮相變。

2．2 顆粒運動方程

顆粒的受力決定了顆粒的運動軌跡。除了重力、阻力外，這里還要考慮Saffman升力FS、虛擬質量力FV和壓力梯度力FP。

固體顆粒運動方程為：

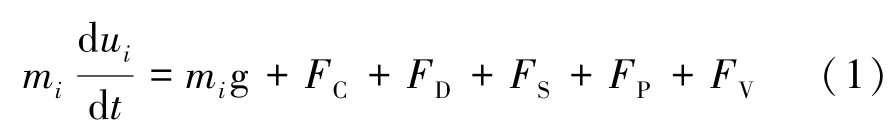
式中mi為顆粒質量；u i為顆粒速度；FC和FD分別為顆粒被液體攜帶過程中受到的離心力和阻力。

FS、FV和FP分別為：

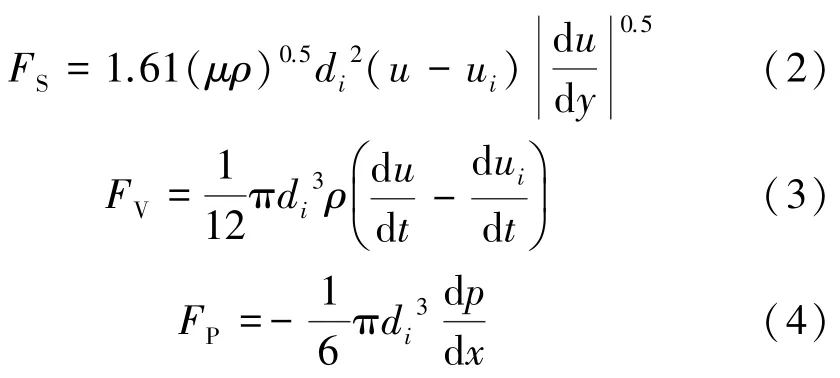
式中ρ為流體密度；μ為流體動力黏度；u為流體流動速度。

2．3 EDEM-Fluent耦合

本文應用歐拉-拉格朗日模型進行固液兩相耦合。利用ANSYS Fluent在歐拉坐標系下對液相進行計算，控制方程采用基于時均的Navier-Stokes方程，湍流模型采用標準κ-ε湍流模型，用SIMPLEC算法進行壓力和速度耦合，對流項及擴散項均采用二階中心差分格式。計算域的進口采用速度進口邊界條件，出口采用出流邊界條件，在各過流部件表面設置無滑移邊界條件，近壁面區流動采用標準壁面函數處理。數值模擬中，各監測量的收斂精度統一設為10－5。

利用EDEM在拉格朗日坐標系下對固相顆粒進行求解，設定顆粒為單一粒徑的球形。模擬過程中不考慮熱交換。顆粒與顆粒間的接觸模型選用Hertz-Mindlin無滑移模型［7－8］。在該模型中，法向力分量的計算基于Hertz接觸理論，切向力分量的計算則基于Mindlin-Deresiewicz的工作［9－10］。顆粒與輸送泵過流部件壁面之間的接觸采用Hertz-Mindlin模型和Archard磨損模型共同處理［11］。

2．4 Archard磨損模型

Archard磨損模型的表達式為：

式中Q為去除材料的體積即磨損體積，mm3；Fn為法向力；dt為滑動距離，m；W為磨損系數，可表示為：

式中K為無量綱常數；H為最軟表面的硬度值。

式中h為磨損深度；A為磨損區域面積，EDEM中采用磨損深度表示單位面積的磨損量。

2．5 網格劃分

利用ICEM CFD商用軟件對各過流部件進行網格劃分，各部分計算區域均采用非結構四面體網格進行離散，對近壁面區網格進行加密。經過網格無關性檢查，最后確定網格劃分方案。最終確定的網格方案中，4個計算子區域的網格數如表2所示。

表2 各計算子區域的網格數

3 結果與討論

將輸送泵進口的固相質量分數設為10%。選取顆粒粒徑d＝1．0～4．0 mm工況進行流動模擬。為檢查模擬中固相的質量守恒，在輸送泵啟動過程中，選取d＝2．0 mm和4．0 mm進行泵內顆粒總質量比較。計算得到的泵內固體顆粒總質量隨時間的變化如圖3所示。泵啟動后，泵內顆粒質量不斷增加，0．3 s后，2種顆粒粒徑工況下的泵內顆粒總質量達到平衡，泵進入平穩運行階段。以下在t＝0．408 16 s（葉輪旋轉10個周期所需的時間）后對模擬結果進行分析與討論。

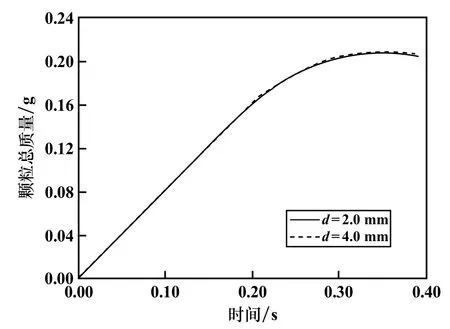
圖3 不同粒徑工況下泵內顆粒質量在泵啟動過程中的變化

3．1 顆粒粒徑對葉輪磨損的影響

圖4為輸送泵葉輪各過流部件的平均磨損深度隨顆粒粒徑的變化情況。可以看出，隨著顆粒粒徑增大，長葉片平均磨損深度逐漸減小，短葉片平均磨損深度顯著增加，后蓋板平均磨損深度先增大后減小。相比之下，前蓋板平均磨損深度較小，隨著顆粒粒徑增加呈現逐漸增大的趨勢。

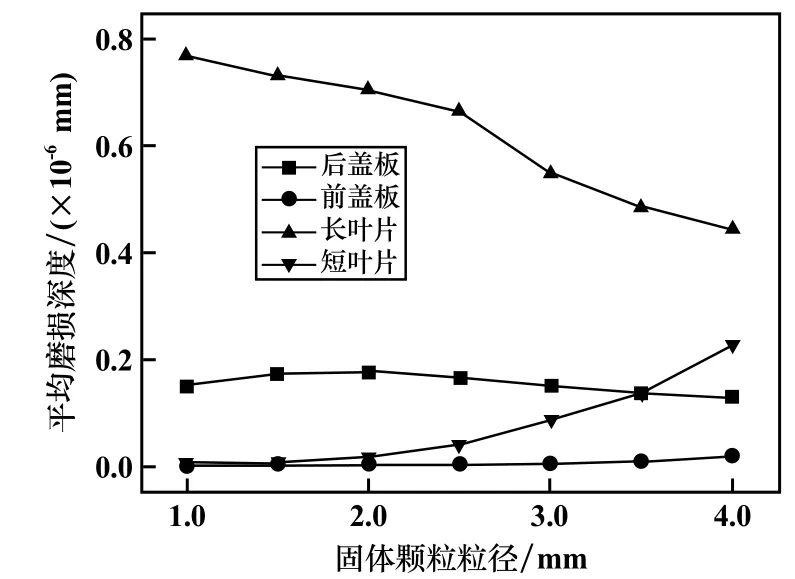
圖4 葉輪各部件平均磨損深度隨顆粒粒徑的變化

圖5為輸送泵葉輪各過流部件的最大磨損深度隨顆粒粒徑的變化情況。最大磨損深度表征葉輪各部件磨損最嚴重區域的磨損情況，前蓋板、后蓋板、短葉片的最大磨損深度變化情況與平均磨損深度變化趨勢相近。值得注意的是，長葉片的最大磨損深度在d＝2．5 mm時達到峰值，隨著顆粒粒徑進一步增大，最大磨損深度減小。

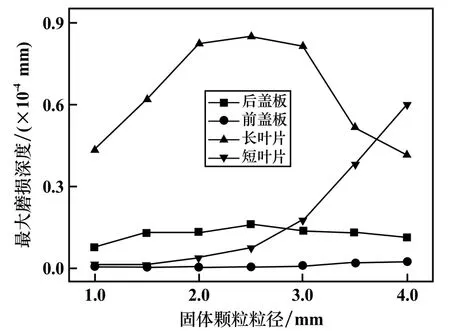
圖5 葉輪各部件最大磨損深度隨顆粒粒徑的變化

表3為同一磨損時刻葉輪各部件的磨損深度分布隨顆粒粒徑的變化情況。可見葉輪各部件均出現不同程度的磨損。葉片磨損較為嚴重，集中在葉片進口處和葉片工作面出口靠近后蓋板的位置。

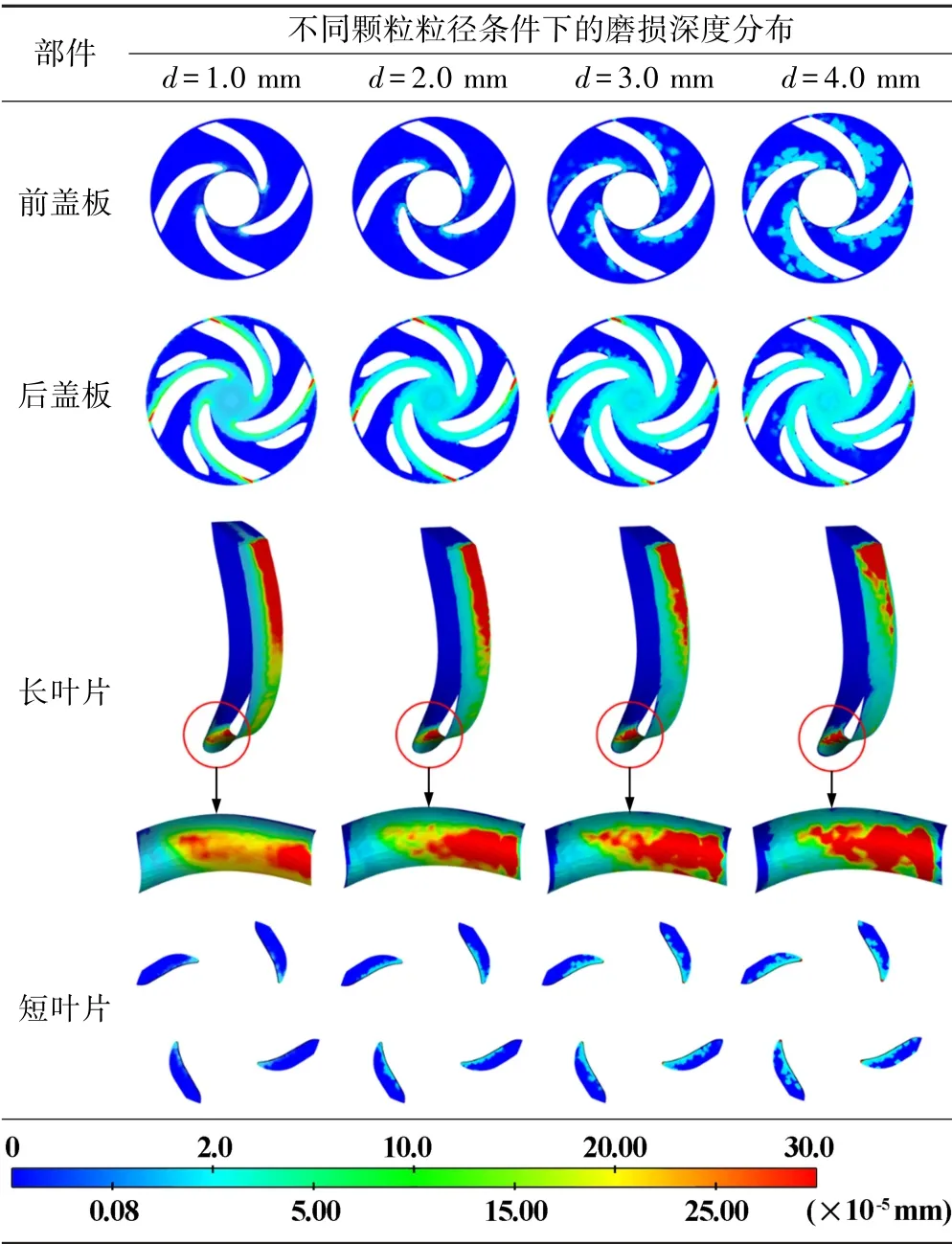
表3 葉輪各部件磨損深度分布

隨著顆粒粒徑增大，前蓋板表面呈現塊狀磨損狀態，說明大顆粒在葉輪中運動不規則性較強，碰撞前蓋板幾率大，從而造成沖擊磨損。在前蓋板表面，磨損較嚴重的區域位于前蓋板與葉片進口交界處，前蓋板磨損亦隨顆粒粒徑增大而加劇，但與葉輪其他部件相比，磨損深度較小。后蓋板磨損最嚴重的區域位于葉片出口工作面附近。隨著顆粒粒徑增大，后蓋板表面與葉片交界處附近區域的磨損程度有所減輕，但磨損范圍擴大。在后蓋板的中心區域，隨顆粒粒徑增大，顆粒慣性增大，同時顆粒之間的碰撞作用增強，少量顆粒進入葉輪流道后未跟隨葉片運動，而是繼續沿軸向運動，從而對該部位進行沖擊。該部分顆粒無法正常進入葉輪流道，對該區域產生持續性切削作用，從而造成磨損。葉片出口工作面靠近后蓋板位置為嚴重磨損區域，但是隨著顆粒粒徑增大，嚴重磨損區域的面積有所減小；葉片工作面進口與出口之間的區域磨損深度減小。葉片進口的磨損也隨著粒徑增大而加重，葉片進口磨損位置更偏向于后蓋板。在后蓋板上設置的4個短葉片的磨損隨顆粒粒徑增加而加劇，磨損的位置位于短葉片上靠近葉片工作面的區域。

為了驗證數值模擬的物理有效性，在某磨損試驗臺上進行了輸送泵葉輪磨損試驗，所用顆粒粒徑2．0 mm，將泵拆解后獲得的葉輪磨損后照片如圖6所示。可以看出，磨損試驗后，葉片進口處以及葉片出口工作面均產生嚴重磨損，尤其是葉片工作面出口，已被顆粒磨穿。圖6結果與表3一致。

圖6 磨損試驗后的葉輪照片

3．2 顆粒運動分析

圖7為顆粒粒徑1．0 mm和4．0 mm條件下輸送泵內的顆粒速度分布及葉片進口區域的速度矢量分布。

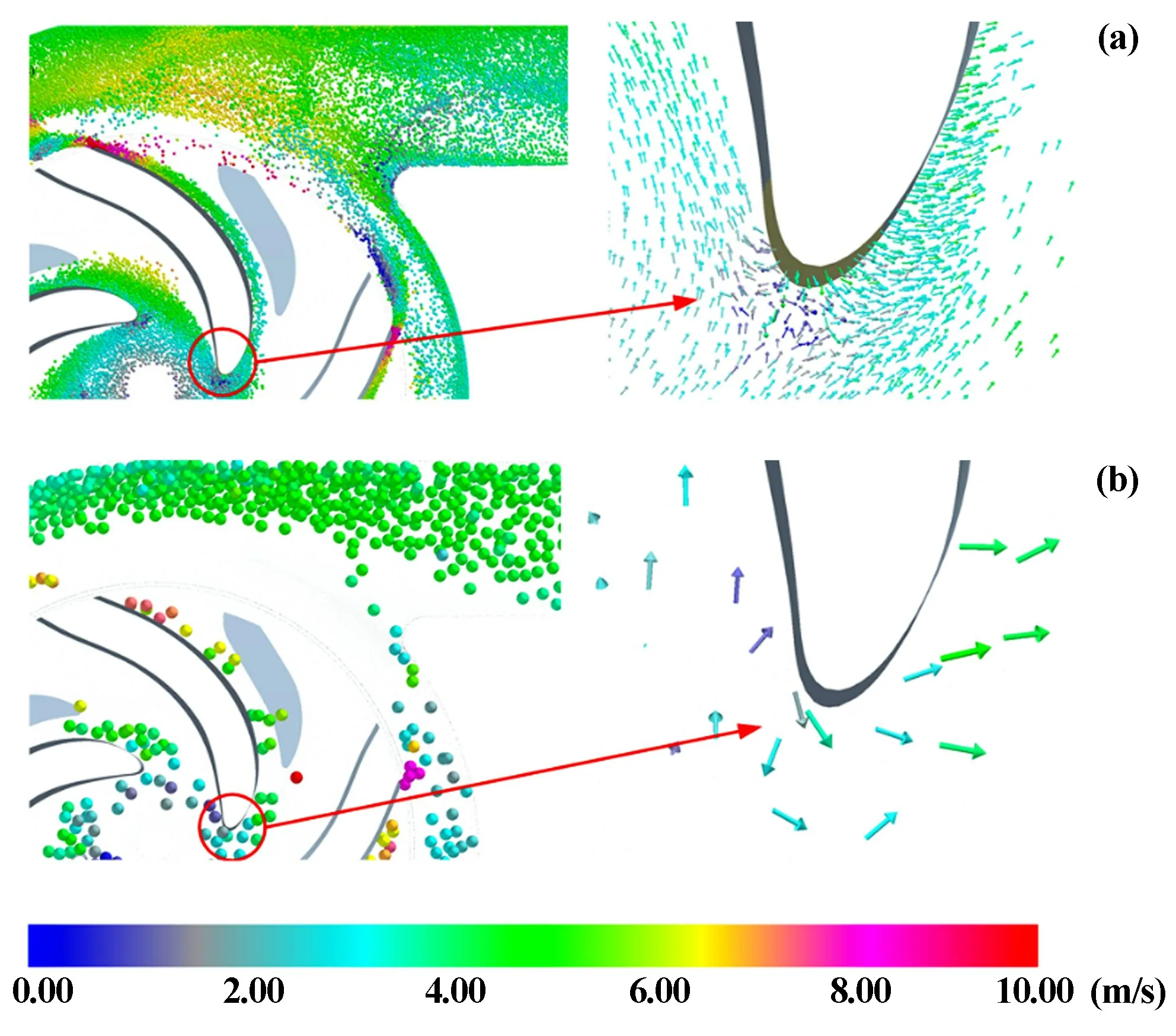
圖7 泵流道內的固體顆粒分布

當d＝1．0 mm時，在葉片進口區域，大量顆粒反復與葉片頭部產生碰撞，產生低速環流區，對葉片頭部進行沖擊，導致磨損。顆粒進入葉輪后，速度方向由軸向逐漸向徑向轉變，有序地沿葉片工作面向下游運動，顆粒運動軌跡與短葉片之間存在明顯間隙，故當顆粒粒徑較小時，短葉片磨損較輕。葉片進口與出口之間的工作面與顆粒之間存在一定間隙，所以該位置磨損量較小。在葉片出口處，顆粒速度驟增，較大的切向速度分量使顆粒沿著葉片出口快速運動，造成橫向切削磨損。

在保證泵進口流量及固相質量分數不變的情況下，隨著顆粒粒徑增大，單個顆粒體積及質量增大，顆粒數減少。葉片進口處顆粒速度與其他粒徑工況相比未發生明顯變化。但質量增大使單個顆粒動能增大，對葉片頭部產生更強的沖擊作用。顆粒慣性以及離心力增大，使顆粒有向葉片背面運動的趨勢，進而與短葉片發生碰撞。顆粒在葉輪流道內的運動更加不規則，部分顆粒運動至短葉片與葉片背面之間的流道。在葉片出口處，隨著顆粒粒徑增大，顆粒運動速度減小，葉片工作面出口的磨損減輕。

為更加直觀地表示不同顆粒粒徑條件下顆粒與壁面的碰撞規律，引入無量綱相對碰撞率N：

表4為不同顆粒粒徑條件下，顆粒對長葉片工作面的相對碰撞率。隨著顆粒粒徑增大，顆粒對長葉片工作面的相對碰撞率減小，說明顆粒撞擊長葉片工作面的幾率下降，顆粒有遠離長葉片工作面的趨勢。

表4 顆粒粒徑對長葉片工作面的相對碰撞率

4 結 論

1）葉片磨損集中在長葉片工作面出口和葉片進口位置。隨著顆粒粒徑增大，長葉片平均磨損深度減小，但其最大磨損深度先增加后減小。

2）葉片背面磨損總體較輕。隨著顆粒粒徑增大，葉片進口磨損不斷加重，而葉片工作面磨損量減小。

3）隨著顆粒粒徑增大，顆粒撞擊葉輪工作面幾率減小，顆粒有向葉片背面運動的趨勢，部分顆粒沖擊短葉片，顆粒運動不規則性增強。