鹽堿土入滲下修正Green-Ampt模型參數確定與驗證

陳俊英，何旭佳，楊亞龍，白旭乾，李 毅，謝林林

（1. 西北農林科技大學旱區農業水土工程教育部重點實驗室，楊凌 712100；2. 西北農林科技大學水利與建筑工程學院，楊凌712100；3. 西北農林科技大學理學院，楊凌 712100）

0 引 言

鹽堿土是堿土與鹽土的總稱，在中國總面積超過0.33億hm2，占灌溉面積的15%[1]。土壤中的鹽分離子影響作物水分吸收，對作物生長造成危害[2]。鹽堿土的改良利用與鹽堿土的入滲規律研究息息相關，掌握鹽堿土的入滲特性，建立鹽堿土的入滲模型尤為重要。

Green-Ampt模型是1911年Green與Ampt根據土壤毛管理論提出的土壤入滲模型[3]，計算精度較高，因而得到廣泛應用。隨著研究深入，Green-Ampt模型不斷被修正應用于初始含水率不均的土層入滲[4]、層狀土[5-6]以及渾水入滲[7]、降雨入滲[8]等研究領域，證明了該模型擁有廣泛的適用性。趙偉霞等[9]建立了適用于恒定水頭井積水入滲的Green-Ampt模型，聯立入滲率與累計入滲量的表達式，反求土壤導水率與濕潤鋒面基質吸力，并發現恒定水頭井入滲下土壤濕潤體呈橢球體。Ma等[10]對大型分層土壤土柱進行擴大試驗，采用了Bouwer方法對Green-Ampt模型進行修正，修正模型模擬效果良好。針對Green-Ampt模型的修正集中在土壤導水率與濕潤鋒面基質吸力兩個參數的變換求解，問題難度較高。迄今已有大量使用該入滲模型擬合鹽堿土入滲過程的研究，周蓓蓓等[11]施加枯草芽孢桿菌改良鹽堿土，并分別采用Philip和Green-Amp模型擬合入滲數據，結果顯示Green-Ampt模型的擬合數據誤差小于Philip模型。這與王全九等[12]的研究成果相似，都證明了在入滲時間較長的情況下，Green-Ampt模型模擬精度更高。鹽堿土由于鹽分離子的存在，其入滲性能降低，入滲歷時較普通土壤更長[13]，采用Green-Ampt模型更適合描述鹽堿土水分運移規律。不同于Kostiakov等經驗模型，Green-Ampt模型具有堅實的理論基礎，可以不斷被修正從而適用于鹽堿土入滲。因此采用Green-Ampt模型模擬鹽堿土入滲過程具有明顯優勢，但目前還未有固定的通用于鹽堿土入滲的修正Green-Ampt模型。

本文根據鹽堿土的入滲特性采用入滲區含水量剖面分布假定，通過擴散率計算得到基質吸力值從而對傳統Green-Ampt模型進行修正，建立適用于鹽堿土的修正Green-Ampt入滲模型，并采用試驗數據驗證該模型。修正模型綜合考慮鹽堿土入滲機理，結合水分入滲過程，進一步提高了入滲預測模型的精度，高精度的水分入滲預測作為基礎研究可為鹽堿土的改良利用與農業生產提供理論依據與技術支持。

1 基本理論

1.1 Green-Ampt模型基本表達式

Green-Ampt模型針對出現薄層積水時干燥土壤的入滲問題，假定入滲中存在明顯的水平濕潤鋒面，將濕潤區與未濕潤區分開，入滲時的水分運移符合達西定律。模型基本表達式[3]為

式中i(t)為入滲率，cm/min；Ks為飽和導水率，cm/min；Sf為濕潤鋒面基質吸力，cm；Zf為濕潤鋒運移深度，cm；H為土壤表層積水深度，cm。

由水量平衡原理，推得累積入滲量與濕潤鋒運移深度的表達式為

式中I為累積入滲量，cm；θs為土壤飽和含水率，%；θi為土壤初始含水率，%。

利用式（1）和式（2）推得時間與濕潤鋒關系式為

式中t為時間，min。

1.2 修正Green-Ampt模型

1.2.1 基本假設與理論

對于Green-Ampt模型，應用時要解決的最重要問題，即確定模型兩大參數飽和導水率Ks與基質吸力Sf。在傳統模型的實際應用中，由于空氣的存在，土壤的飽和區并不能完全被水填滿，因此飽和區的實際導水率K0會小于理論上的飽和導水率Ks，地表實際含水率值θ0會小于土壤飽和含水率θs[14-16]。有研究表明(θ0-θi)與K0不準確造成的數據結果差異大于Sf不準確造成的差異，因此確定(θ0-θi)與K0的數值是至關重要的[17]。

本研究對修正Green-Ampt模型作以下假設：

1）考慮到鹽堿土由于鹽分離子的存在，入滲時長高于普通土壤，甚至出現水分難以下滲的現象[18]，假設試驗計劃濕潤鋒深度足夠深，入滲時間足夠長，認為上層土壤接近飽和，入滲率趨于穩定。則有兩個結論：①K0數值等于土壤穩定入滲率ie，為1/2的飽和導水率[19]；② 土壤上層飽和區的地表實際含水率θ0等于入滲時間超過24 h的土壤表層實測含水率θm。

2）由于鹽堿土為非飽和土，假定水分到達的區域為入滲區，將入滲區分為濕潤區與浸潤區，含水量分布如圖1所示，濕潤區導水率K=ie且含水率θ=θm，浸潤區含水率由θm到θi變化。對濕潤區作以下假設：①當濕潤鋒運移深度為L時，濕潤區深度為L/α(α的取值范圍為1～10)；②有研究證明土壤浸潤區的含水率分布采用橢圓曲線描述具有較高精度[20]，因此入滲時用1/4的橢圓曲線描述浸潤層含水量變化，溫馨等[21]經研究獲得濕潤區深度為L/2時入滲深度的隱性表達式，本研究將濕潤區深度設為L/α，得出不同入滲時刻t(min)下，濕潤鋒運移深度L(cm)的隱性表達式

式中ie為土壤穩定入滲率，cm/min；θm為土壤表層實測含水率，%；α為表征濕潤區深度時使用的參數，無物理意義。

由此，將Green-Ampt模型中的Ks數值替換為穩滲率ie，修正Green-Ampt模型的表達式為

1.2.2 參數推導

根據Philip的研究[22-23]，傳統Green-Ampt模型實質上是將土壤水分運動參數近似為δ函數，即用一個含水率處急驟上升的δ函數來近似代替土壤擴散率D(θ)，而擴散率D隨含水率發生變化，土壤含水率較大時，擴散率急速增大，因此模型計算的土壤濕潤鋒吸力Sf值與實際數值有較大差距。Sf值的修正方法本質是用一條D=D’的線性化直線近似表達土壤水分運動參數D(θ)，避免了擴散率D(θ)因含水率的增加而急速上升的現象，從而增加了Sf計算值的準確度。

令D'表示濕潤區某種平均的或有效的土壤擴散率，已知Zf與t有近似關系式[24]

使用ORIGIN軟件通過最小二乘法擬合試驗數據Zf與t，擬合形式為：Zf=λ·t0.5（λ為擬合時使用的參數，無物理意義）。則有D'=λ2/2，通過擬合結果得到D'值。

而D'的表達式為

根據對Green-Ampt模型的兩個假設，將土壤飽和導水率Ks替換為穩滲率ie，將土壤飽和含水率θs變為土壤表層實測含水率θm，式（7）可寫為

將定值ie、H、θm、θi代入式（8），得Sf值。

綜上，Green-Ampt模型修正后兩大參數Ks與Sf都可得到準確數值。在入滲時間足夠長的情況下，將Ks轉換為更易得的穩滲率ie，并通過將土壤水分參數D(θ)近似線性化，經ORIGIN軟件擬合后得到更準確的Sf值，避免了含水率增大對D(θ)的影響。

為進一步探究修正模型精度，引用郭向紅等[25]建立的Green-Ampt模型模擬鹽堿土的入滲過程，比較兩種模型模擬效果，確定模擬效果造成差異的原因。郭向紅模型與修正模型基本假定相同，因此可引用該模型模擬鹽堿土的入滲過程，并探究郭向紅模型模擬鹽堿土入滲的精度。為了研究不同水頭下的水分入滲情況，基于傳統Green-Ampt模型的基本假定，即土壤初始含水率分布均勻且存在明顯的濕潤鋒，郭向紅等采用入滲率與濕潤鋒運移深度的倒數呈線性關系這一理論依據，求得概化濕潤鋒深度，通過擬合入滲率數據與概化濕潤鋒，求得參數a、b值，計算得飽和導水率Ks與基質吸力值Sf。

將Ks代入式（3），利用MATLAB采用二分法解不同時刻t對應的Zf，將解出的Zf代入式（1），即可求出不同時刻對應的入滲率。

2 材料與方法

2.1 試供土樣

試驗土壤均取自于內蒙古河套地區沙壕渠灌域，在灌域內隨機選取12個采樣點，采集0～30 cm深度表層土，經風干、研磨、過篩后得到土樣。土壤含水率由烘干法測得，使用pH試紙測得土壤pH值，采用激光粒度儀Mastersizer-APA2000測得土壤顆粒組成，對鹽堿土易溶鹽離子的含量進行測定。經測定后獲取到易溶鹽總量與8種主要的易溶鹽離子CO32-、HCO3-、SO42-、Cl-、Ca2+、Mg2+、K+、Na+含量。根據鹽漬化分級標準的易溶鹽總量確定鹽堿土的鹽漬化程度，12個采樣點的鹽堿土樣品分別為2個輕度鹽堿土、2個中度鹽堿土、2個重度鹽堿土，其他6種均為鹽土。因此樣品中的輕度鹽堿土、中度鹽堿土與隨機選取的1個重度鹽堿土構成了本文所用的5種土壤類型，根據5種試驗土樣驗證修正Green-Ampt模型的適用性，其基本理化參數見表1。

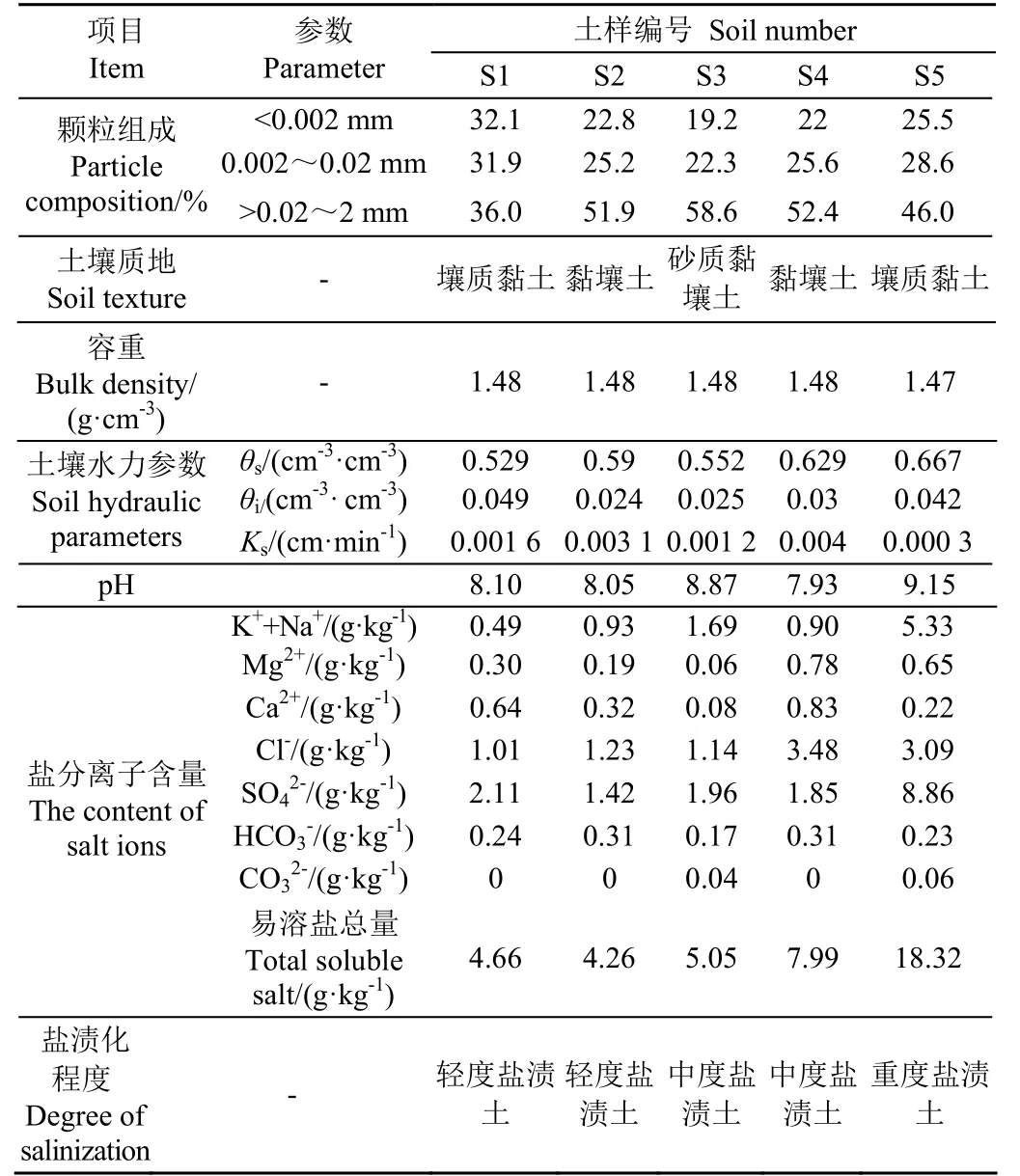
表1 試驗土樣理化參數Table 1 Physical and chemical parameters of test soil samples

2.2 試驗方案

試驗地點位于陜西西北農林科技大學旱研院灌溉大廳，試驗為一維垂直積水入滲試驗，裝置圖見圖2。裝置由試驗土柱、供水設備和支架組成，試驗土柱采用有機玻璃材料制造，柱高70 cm，內徑為12 cm，裝土高為60 cm，下置透氣底板。供水設備為內徑10 cm的馬氏瓶。試驗土柱與馬氏瓶外壁均有刻度，以便觀察讀數。

將試驗土樣混合均勻，風干后過2 mm篩備用。灌溉用水為咸陽市楊陵區自來水。利用馬氏瓶供水，供水水頭始終控制為3 cm。在試驗過程中，按照先密后疏的時間間隔定時觀察數據，記錄土柱濕潤鋒運移深度和馬氏瓶水位數據。經預試驗確定計劃濕潤鋒為30 cm，即當濕潤鋒達到30 cm時停止供水，結束試驗。

環境溫度控制在24 ℃左右，蒸發忽略不計，每種鹽堿土入滲試驗重復3次。

2.3 數據處理

將修正Green-Ampt模型與郭向紅模型計算的入滲率進行對比，分析兩者模擬效果的差異。為評價模型模擬精度，將修正Green-Ampt模型模擬值與實測值進行相關分析，并使用決定系數R2與平均絕對誤差MAE作為評價指標。采用軟件SPSS19.0進行分析。

3 結果與分析

3.1 參數確定

3.1.1 修正Green-Ampt模型

根據式（8）求得土壤水分運動參數Sf。

根據對Green-Ampt模型的假設，認為鹽堿土試驗計劃濕潤鋒深度足夠深，入滲時間足夠長，Ks數值等于土壤穩定入滲率ie。

5種鹽堿土采用修正Green-Ampt模型計算的Ks與Sf值見表2。

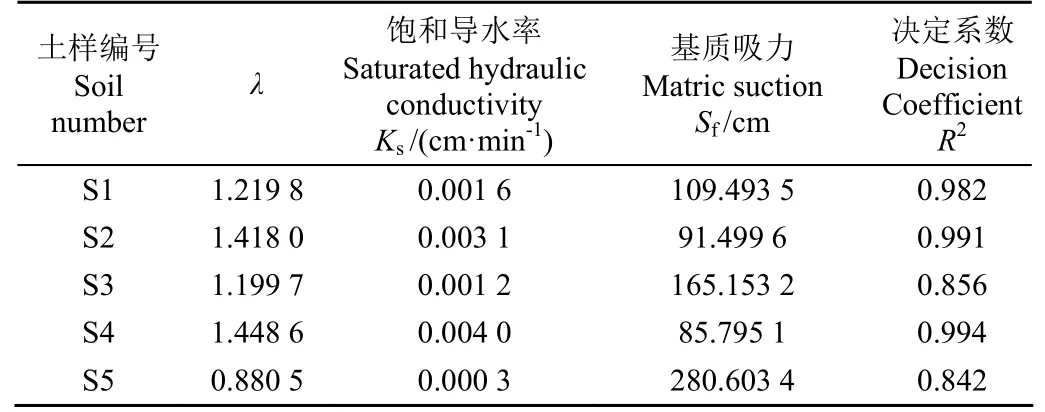
表2 修正Green-Ampt模型Ks與Sf值匯總Table 2 Summary of Ks and Sf values of improved Green-Ampt model

3.1.2 郭向紅模型

根據試驗方案確定入滲水頭為定值，即H=3 cm。求得概化濕潤鋒深度后，經擬合概化濕潤鋒深度的倒數與試驗入滲率的關系計算Ks與Sf值。5種鹽堿土的Ks與Sf值見表3。

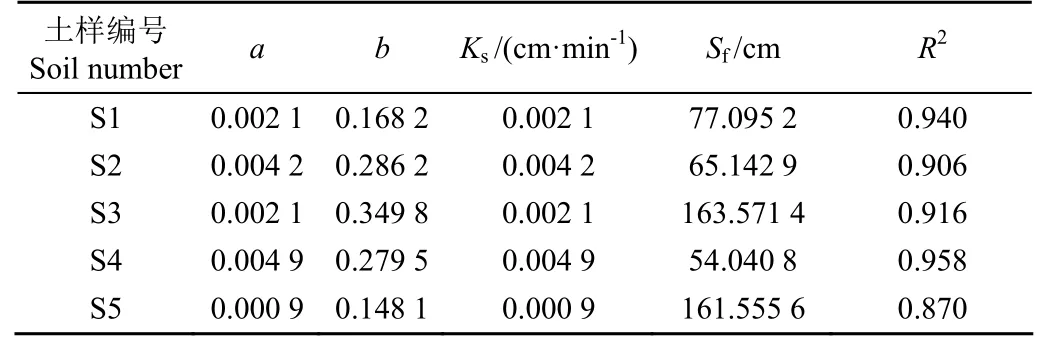
表3 郭向紅模型Ks與Sf值匯總Table 3 Summary of Ks and Sf values of Guo Green-Ampt model

3.2 模型參數與含鹽量分析

土壤入滲Green-Ampt模型的兩大參數Ks與Sf值由土壤性質確定。在灌溉水樣一致、裝土容重相同的情況下，土壤自身特性是影響模型參數的主要因素，作為鹽堿土，鹽分含量對土壤的模型參數有重要影響。將修正模型參數值與鹽堿土含鹽量進行分析。根據土壤中鹽分離子電動電位從小到大的排序（Ca2+＜Mg2+＜H+＜NH4+＜K+＜Na+），K+和Na+電動電位大，分散性強而凝聚性弱，即加強土壤顆粒的分散性并降低土壤團聚體的穩定性，較短時間內使土壤的大孔隙崩塌，小孔隙堵塞，降低土壤對水和空氣的滲透性，降低導水率，即這兩種離子最大程度上會影響土壤入滲能力，改變土壤入滲模型參數。因此取K++Na+與易溶鹽總量作為衡量土壤含鹽量的兩大指標。

5種鹽堿土修正Green-Ampt模型參數值與含鹽量指標見表4。根據表4可以看出，Ks、Sf與易溶鹽總量無明顯規律，但是與K++Na+存在一定規律，除S1外其他4種鹽堿土的參數值Ks隨K++Na+含量的增大而減小，Sf隨K++Na+含量的增大而增大。

表4 修正模型參數值與含鹽量指標匯總Table 4 Summary of improved model parameter values and salt content index

由于模型參數受K++Na+的影響，選擇S2、S3、S4、S5的K++Na+含量分別與Ks、Sf值進行回歸分析，分別采用冪函數模型與對數函數模型進行回歸估計。決定系數和檢驗值結果見表5。

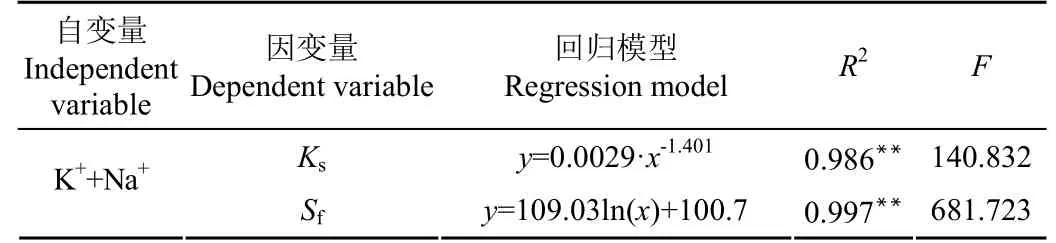
表5 飽和導水率、基質吸力與K++Na+含量回歸分析結果Table 5 Regression analysis results of saturated hydraulic conductivity, matric suction, and K++Na+ content

從表5可以看出，采用冪函數模型對K++Na+與Ks值進行回歸分析，R2值大于0.95；采用對數函數模型對K++Na+與Sf值進行回歸分析，R2值大于0.99。因此兩種模型擬合的顯著性檢驗都具有統計意義。

3.3 模型驗證與對比

3.3.1 入滲率驗證與對比

將修正Green-Ampt模型計算的Ks與Sf值代入式（5），郭向紅模型通過式（3）采用二分法解出Zf代入式（1），可求出兩種模型不同時刻對應的入滲率，將模型計算結果與實測數據進行對比，探究其模擬入滲效果的準確度。5種鹽堿土的入滲率比較結果點繪于圖3。

如圖3所示，修正Green-Ampt模型計算的入滲率在整體上更接近于實測值，特別在曲線的后半段，郭向紅模型與實測值差距較大，而修正Green-Ampt模型與實測值更為接近。由圖3中S3曲線可見，郭向紅模型計算值與實測值差距明顯，顯著高于實測值，而修正Green-Ampt模型的數據曲線與實測值曲線基本一致。因此根據圖3顯示，修正Green-Ampt模型的入滲率數據更接近于5種鹽堿土的實測值。

將郭向紅模型、修正Green-Ampt模型計算的入滲率與實測值進行相關分析，以衡量兩組數據的接近程度，見表6。

表6 顯示，對于試驗所用的5種鹽堿土，修正模型計算的入滲率R2平均值為0.983，且58種鹽堿土R2值均高于0.95，呈現極強相關性。修正模型模擬值的MAE均小于0.05 cm/min，MAE最大值的平均值分別為0.048和0.029 cm/min。綜合R2值與MAE兩個指標，修正Green-Ampt模型預測值誤差較小，模擬精度較高。郭向紅模型入滲率R2平均值為0.932，MAE平均值為0.055 cm/min，總體與實測值存在一定差距，特別在曲線后半段其計算值高于實測值。總體看來，修正Green-Ampt模型模擬的入滲率曲線更接近實測值，更適用于鹽堿土入滲分析。

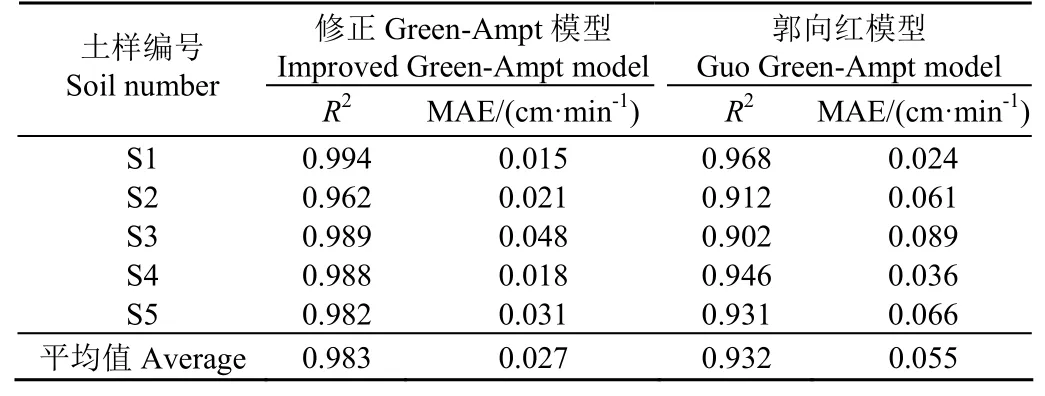
表6 入滲率相關分析結果匯總Table 6 Summary of related analysis results of infiltration rate

3.3.2 濕潤鋒運移深度驗證

因為郭向紅模型中的濕潤鋒為概化濕潤鋒，因此只利用濕潤鋒實測值驗證修正模型的適用性，不進行兩種模型模擬效果的對比。修正Green-Ampt模型的驗證是通過MATLAB建立代碼表達式（4），α定義為從1到10步長為0.1的循環，精度為0.001，將1種鹽堿土的Δθ、t、Sf、K代入計算得91個數組（橫軸為α，縱軸為時間），5種鹽堿土重復5次操作。將91個數組與對應鹽堿土的濕潤鋒實測值進行相關分析，當α取值為1時與實測值最接近，隨著α的增加，實測值與模擬值的差距越來越大，嚴重偏離實際情況（當α取值為1.1時與實際情況已出現較大差異）。因此，α取值為1，濕潤層深度為L。出現此情況是由于所取鹽堿土的鹽分與土壤質地共同影響。由表1可以得知5種鹽堿土的質地偏黏，土壤顆粒中黏粒占據一定比例，黏土在巖土工程中被稱為飽和土，水會占據土壤孔隙的絕大部分體積，土壤持水能力強。其次，5種鹽堿土中含有大量K+和Na+，兩種離子電動電位大，對土壤顆粒的分散作用強，會減弱對下層土壤的導水能力。

將修正Green-Ampt模型所計算的不同時刻的濕潤鋒運移深度與實測值進行對比，分析模型精度。將5種鹽堿土的濕潤鋒運移深度點繪于圖4。

如圖4所示，修正Green-Ampt模型與實測值的差異整體上較小，圖4中S1曲線顯示模擬值與實測值趨勢基本相同，S2、S4模擬曲線與實測值比較接近。S3、S5曲線有明顯拐點，拐點前模擬值小于實測值，拐點后模擬值大于實測值。將此現象結合鹽堿土的鹽分離子含量進行分析，K+和Na+分散性強凝聚性弱，降低土壤導水率[26-27]，S3、S5的K++Na+含量分別為1.69、5.33 g/kg，而其他3種土均小于1 g/kg，因此在拐點處鹽分向下運動不斷累積，土壤水溶液的K+和Na+到達一定濃度，使土壤顆粒分散，導水能力出現明顯衰減，濕潤鋒向下運移的速率減緩。

此外，S5的濕潤鋒運移距離只到達25 cm，與預期濕潤層30 cm出現矛盾。原因在于S5是唯一的重度鹽堿土，土壤質地為壤質黏土。黏土持水能力強、易飽和，又由于鹽分離子隨著水分運動的下移不斷累積，堆積形成障礙層，兩者共同影響從而使水分無法下滲。

5種鹽堿土修正模型計算的R2平均值為0.868，S1的R2最高，為0.952。修正模型計算的MAE平均值為2.639 cm，且5種鹽堿土MAE數據均小于3.50 cm，修正模型中S1的MAE值最小，為1.185 cm。分析結果證明修正模型的預測值與實測值較為接近，數據誤差較小，其中S1實測值與模型計算值一致性較高。

4 討 論

4.1 S1含鹽量與修正模型參數分析

模型參數與含鹽量分析中，S1不符合Ks隨K++Na+含量的增大而減小、Sf隨K++Na+含量的增大而增大的規律。5種鹽堿土中S1含鹽量指標K++Na+含量最少，而模型參數值Ks卻并非最高，原因在于與其他鹽堿土相比，S1作為輕度鹽堿土，其Ca2+、Mg2+離子含量較高，且pH值為8.10，屬堿性。在水分的入滲過程中，土壤膠體上的Ca2+、Mg2+離子被Na+置換到土壤溶液中，從而形成一種微溶物和一種沉淀，分別為Ca(OH)2、Mg(OH)2，這些物質在土壤中大量累積堵塞土壤孔隙，使水分和空氣無法透過，降低土壤的導水能力。另外，S1為壤質黏土，與作為重度鹽堿土的S5質地相同。而壤質黏土與其他土壤相比，由于土壤顆粒本身含有較多黏粒，在入滲過程中勢必會降低土壤的入滲性能[28-29]，使土壤表現出特殊性。

S1修正模型參數值Sf不符合規律的原因在于其黏重的質地。根據國際制土壤質地分類標準，S1中的黏粒（土壤顆粒粒徑小于0.002 mm）含量在5種鹽堿土中位居首位（表1）。Sf存在一定表達式[6]，說明其值受土壤進氣吸力ψb、形狀系數n、土壤表層積水深度H與位置水頭Z共同影響。對于本文H與Z都是定值，H取3 cm，Z定值為0，而ψb、n與土壤質地關聯緊密。一般地說，粗質地砂性土壤或結構良好的土壤其進氣值是比較小的，而細質地的黏性土壤其進氣值相對較大[30]，S1黏重的質地使其ψb數值變大。土壤孔徑分布要取決于土壤質地，質地越黏，土壤形成細小的無效水孔徑越多，較大的有效水孔徑越少[31]，用RETC軟件選用VG公式擬合5種鹽堿土的土壤水分特征曲線得到參數n值，S1、S2、S3、S4、S5的n值分別為2.162、2.189、2.306、2.165、2.408，S1的n值最小。S1的ψb數值大且n值小，因此出現了S1的Sf值偏大，不符合規律的特殊現象。

4.2 模型入滲率模擬值對比分析

入滲率驗證與對比中，修正Green-Ampt模型模擬精度高于郭向紅模型。這是由于修正模型計算的模型兩大參數Ks與Sf值比郭向紅模型更精確，更接近其理論值。郭向紅模型的參數計算誤差主要發生在曲線擬合處，即擬合入滲率與概化濕潤鋒運移深度的關系這一部分，出現誤差的原因在于試驗數據會受到各種外界因素干擾，特別是在入滲初期，入滲水頭會產生波動，土壤入滲情況會受到擾動直至入滲穩定，而在入滲末期由于這5種鹽堿土中含有黏土顆粒，甚至會出現入滲率數據非常小、水分幾乎無法向下滲透的情況，在曲線擬合時入滲初期與入滲末期的數據都會對曲線擬合的參數值大小產生影響。由于擬合曲線的縱截距等于Ks值，且試驗所用鹽堿土都為黏壤土，Ks數量級很小，因此入滲數據的微小變化都會使Ks值發生較大改變，Sf受Ks影響數據也會產生偏差。修正的Green-Ampt模型通過將土壤水分運動參數D(θ)線性化，計算出的Sf值更接近理論值，Ks數據由試驗實測確定，因此模型計算結果更貼近實測值。但是考慮到兩種模型最初的最佳適用條件不同，郭向紅模型使用于不同入滲水頭下的入滲試驗，而本研究的修正模型本就使用于鹽堿土的入滲試驗，因此該對比具有一定限制性。修正模型計算值與實測值不完全一致是因為：試驗數據易受環境擾動且土壤初始含水率極低，因此在入滲初期水分以極快速度濕潤土體，入滲率往往會大于模型計算值。

4.3 修正模型模擬誤差原因確定

濕潤鋒運移深度驗證中，忽略由于鹽分離子影響而使濕潤鋒出現拐點的S3與S5，其他3種土的模型預測值均小于計算值，即對應時刻的預測值小于試驗的濕潤鋒實測值，原因在于兩點：1）濕潤區的確定，α定義為從1到10步長為0.1的循環，當α取值為1時模型濕潤鋒計算值小于實測值，而當α取值為1.1（濕潤區為10/11 L）時模型計算值大于實測值，因此存在相對于濕潤區占比很小的浸潤區；2）在試驗開始階段，表層土壤會以極快速度被潤濕，濕潤鋒快速下移，影響后期濕潤鋒運移實測值，因此模型計算值通常小于實測值。

4.4 修正模型的限制性

研究鹽堿土的入滲特性對于其改良利用有至關重要的意義，目前還未建立鹽堿土的入滲模型。由于鹽堿土鹽分離子的存在使其入滲時長大于普通土壤，采用對長時間入滲模擬具有較高精度Green-Ampt入滲模型模擬鹽堿土入滲。本文在傳統Green-Ampt入滲模型的基礎上根據鹽堿土的入滲特性引進擴散率D(θ)對模型進行修正，考慮了土壤中空氣的存在并通過線性化表達D(θ)的方法，提高了模型參數的準確性，該研究對加深鹽堿土農業灌溉研究與加快鹽堿土農業生產起一定推動作用。模型參數受鹽堿土自身特性影響，此處探究了含鹽量與模型參數的變化規律，發現參數值Ks隨K++Na+含量的增大而減小，Sf隨K++Na+含量的增大而增大。樊貴盛等[32]通過大田鹽堿荒地入滲試驗證明了入滲能力、穩定入滲率與K++Na+呈負相關，本文得到的部分結論與之類似。該研究建立的修正Green-Ampt模型經檢驗可應用于土壤質地較為黏重的鹽堿土入滲模型研究中，進行不同鹽漬化程度的鹽堿土入滲過程模擬，當鹽堿土離子成分與試驗土樣不同時，該模型依然適用。但對于不同土壤質地的鹽堿土，如砂土含量極高的鹽堿土，該模型具有一定限制性。修正Green-Ampt入滲模型的建立還需進行更加深入的研究，作者將在后期的研究中將此作為重點，保證模型在不同質地土壤類型的廣泛應用。

5 結 論

本文根據鹽堿土的入滲特性對Green-Ampt模型進行修正，確定修正Green-Ampt模型參數并利用入滲數據驗證后，得到以下結論：

1）土壤自身特性是改變修正Green-Ampt模型參數的主要因素，鹽堿土的鹽分含量對土壤的模型參數有重要影響。總體上，修正Green-Ampt模型的Ks值隨K++Na+含量的增大而減小，Sf值隨K++Na+含量的增大而增大。

2）使用室內入滲試驗的入滲率與濕潤鋒數據驗證修正Green-Ampt模型。結果顯示，5種鹽堿土入滲率R2平均值為0.983，且MAE平均值僅為0.027 cm/min；5種鹽堿土濕潤鋒R2平均值為0.868，MAE平均值為2.639 cm。因此該模型具有較高精度，可用于鹽堿土的入滲過程模擬。

修正Green-Ampt模型適用于質地較為黏重的鹽堿土，存在一定的限制性，能否應用于其他土壤類型，需進一步驗證，未來可繼續改進該模型從而適用于其他類型鹽堿土。