基于機器學習的壓力傳感器故障診斷及剩余壽命預測模型研究*
白同元,黃瀚宇,林琳淳,鐘曉瑩,趙志紅
(北京理工大學珠海學院,廣東 珠海519088)
壓力傳感器在生產線上大量應用,實現了壓力閉環伺服控制,而工作環境高溫,存在水汽、多粉塵現象,使其造成經濟損失。因而工廠希望達到對傳感器健康工作狀態進行實時自檢的目的,做到及時提前預報,方能有效預防和解決故障問題,防患于未然,有效節省工廠原材料和設備采購費用。進一步提高生產能效比,降低成本,保障良好的經濟效益。
目前我國把設備壽命預測技術作為我國未來發展的主要方向,通過文獻查閱,從20世紀以來,國內外學者針對工廠設備壽命預測問題分別從傳統統計角度和機器學習角度進行深入研究。傳統統計方法通過大量的數據選擇合適的模型進行訓練,根據閾值理論,對數據進行診斷,相對于其他類型的方法,相對簡單,工作量較少。文獻[1]采用時間序列的預報算法,對傳感器的輸出數據進行預處理,得到具有故障特征的有用信息,達到對序列預測的目的;文獻[2]采用時間序列對溫室傳感器節點數據進行建模,提取數據特征,據此用遺傳BP神經網絡尋找最優的網絡連接權值,實現故障診斷;文獻[3]利用AR模型對測取的信號進行估計和分析,得到故障發生的范圍,并從其中提取參數作為特征向量,以此作為BP神經網絡的訓練樣本,進而實現故障診斷。
另外,目前國內外研究學者主要研究基于機器學習的方法,提出灰色模型、LSTM時間序列預測模型及馬爾科夫模型等對設備壽命進行預測,目前的研究結果模型精度較高,預測較準確。文獻[4]基于LSTM網絡的時間序列異常檢測算法,利用重建值與原始值之間的誤差對序列進行異常概率估計,并通過異常報警閾值實現異常檢測;文獻[5]基于數據維度高、規模大的特點,提出LSTM時間序列對單一傳感器進行時間序列預測。
本文基于時間序列分析方法和機器學習LSTM的壓力傳感器故障預測方法,可分為故障選取、模型優化和模型預測3個過程:
步驟1:基于大量樣本數據集,考慮到壓力傳感器隨機產生故障,且故障頻率逐漸升高的特點,對研究樣本進行選取。
步驟2:將樣本數據集按照7:3的比例進行分類,將70%的數據利用時間序列模型和LSTM模型對數據進行分析,通過對比模型的精度值及預測準確率,對模型優化,進而確定所選模型,便于提取模型的參數,以選定的模型參數對測試集數據進行反復檢驗。
步驟3:將數據集中剩余30%的數據集輸入到模型中,基于數據分類原則對壓力傳感器的設備運行狀態進行識別。
步驟4:根據選取的模型,建立壽命預測模型,采取實時預測,結合判斷準則,推斷設備運行時長。
1 數據來源及處理
研究數據集來源于某廠鋼鐵軋制過程中壓力傳感器真實運行數據集,分別選取5個時間段的數據集,每個數據集72000條觀測值和2個變量,根據數據集1s內有10條觀測值的特性,為進一步提高預測的精度與周期,提取壓力傳感器的運行特性,對數據進行預處理,以秒為單位,分別計算每個單位的測定值的平均值,將每個數據集的觀測值數量由72000條轉為7200條。整理得到的數據集如表1。

表1 預處理后數據集說明表
當壓力傳感器存在故障時,所測得的壓力值會不斷變化,通過已得的模型預測未來的工作狀態,得到壓力傳感器的未來的運行狀態數據,由此需要引入閾值以此判定該點是否為故障點。引入閾值判定方法[6],降低故障的誤報率。
參數閾值的設定對算法的靈敏度和可靠性的影響很大,如果閾值設定過低,則易出現誤報警;如果閾值范圍太大,又會降低算法的靈敏度。函數表達式如公式(1)。

其中:Pt為閾值,為偏差率的平均值,σ為偏差率的標準偏差。和σ由樣本數據求得,通過設定的閾值對預測的數據點進行判別。若n取0.05,且觀測點在區間內則為正常點;若n取3,且觀測點在0.05倍的區間之外、3倍的區間之內則為偏移點;若觀測點偏移程度高于3σ,則為異常點。
結合判別標準,采用無放回隨機抽樣的方式,以06:00-08:00時段為例,以7:3的比例拆分成訓練集和測試集并對數據點進行分類,如表2。
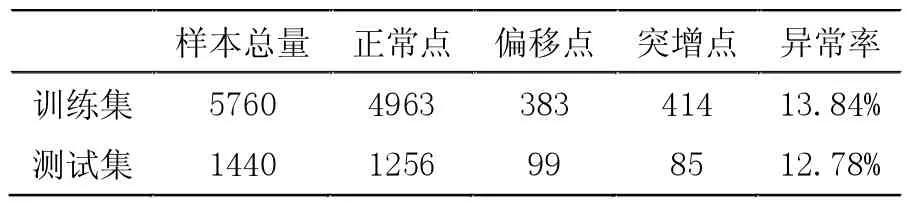
表2 訓練集和測試集數據概況
2 建立時間序列預測模型
本模型為提高模型的預測周期及預測精度,結合壓力傳感器測量計數間隔為0.1s的特點,引入偏離率的概念,即:測定值與設定值之間的偏離誤差,函數表達式如公式(2)。

其中,αm為測定值,βm為設定值,為偏離率。根據文獻[7]可知,AR模型結構如公式(3)。
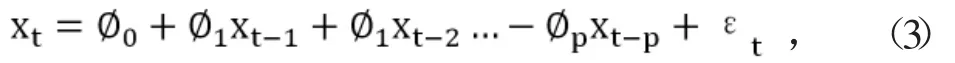
其中,xt為壓力傳感器的偏離率數據序列,εt為白噪聲的誤差項,為模型自回歸系數,對于模型階次的確定,采用赤池信息準則(AIC)進行確定。
為達到提前預測壓力傳感器運行狀態的目的,需對壓力傳感器的運行狀態進行預測,根據文獻[1]可知,AR(n)模型為預測公式如公式(4)。
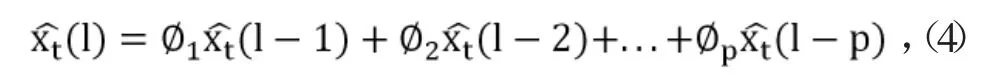
以06:00-08:00時段為例,繪制數據序列圖像,如圖1。
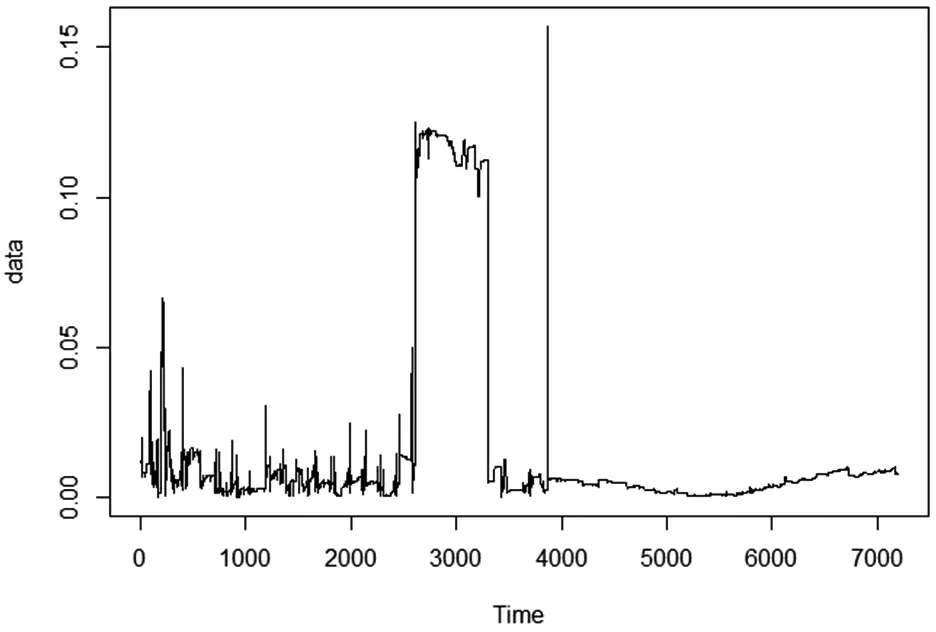
圖1 06:00-08:00時段時間序列圖像
通過圖1觀測,數據無周期性變化,并且無明顯的趨勢性,說明序列平穩,滿足AR模型建模要求。對數據進行自相關系數和偏自相關系數檢驗,得到各個時段的自相關系數和偏自相關系數圖像,如圖2。

圖2 自相關系數和偏自相關系數圖像
由圖2可知,自相關系數圖像拖尾,偏自相關系數圖像隨周期數的增大,偏自相關系數逐漸趨近于0,由此按照AR模型進行建模與預測。
針對自相關系數的拖尾性,偏自相關系數的p值確定為5、7和9。因此我們初步得到AR(5,0,0)、AR(7,0,0)和AR(9,0,0)三組模型,以06:00-08:00時段為例,利用AIC準則,計算這3個模型所對應AIC值,如表3。

表3 模型擬合結果表
同理,通過計算5個時間段的模型AIC值,根據AIC準則,最終確定模型為AR(7,0,0)模型。3時間序列模型預測及精度分析
采取AR(7)模型對測試集進行預測,在測試集中,正常點數為1256個,偏移點數為99個,異常點數為85個;在預測結果中,正常點數為1211個,偏移點數為125個,異常點數為104個。模型準確率為96.42%。
對5組數據利用AR(7)進行預測,平均準確率為96.14%,表明模型預測準確率較高,可以對壓力傳感器運行狀態進行較準確的預測。
計算模型的均方誤差作為模型精度指標的判斷標準,分別得到訓練集和測試集的均方誤差值,如表4。

表4 模型的均方誤差值
由表4計算結果可知,模型的均方誤差值接近于零,說明模型的精度較高,可以準確預測壓力傳感器的運行狀態。
4 建立LSTM預測模型
LSTM模型是一種RNN的變型,最早由Juergen Schmidhuber提出的。通過調節閥門的開關可以實現早期序列對最終結果的影響。
通過設定LSTM模型學習率lr為0.006對測試集進行預測,在測試集中,正常點數為1256個,偏移點數為99個,異常點數為85個;在預測結果中,正常點數為1198個,偏移點數為130個,異常點數為112個。模型準確率為95.38%。
對5組數據利用LSTM進行預測,平均準確率為95.49%,表明模型預測準確率較高,可以對壓力傳感器運行狀態進行較準確的預測。
5 建立設備剩余壽命預測模型
將壓力傳感器全壽命發展歷程可以劃分為3個階段,通過提取相同間隔的壓力傳感器數據,并以偏差率作為研究變量,由圖3正常期階段設備運行時長為240h;根據所設定的數據類別準則,利用公式(1)設置報警閾值,定義若連續5h內均為異常點則下一時間為退化起始點,當運行時長約為264h時,軸承開始退化,隨著退化系數逐漸增大,當偏差率超過失效閾值時,此時軸承已不能繼續工作,此時工作時長為412h。壓力傳感器的壽命如圖3。

圖3 壓力傳感器壽命預測圖
6 結論
本文通過對壓力傳感器的運行狀態利用時間序列分析和機器學習LSTM模型進行建模,根據模型結合數據分類準則對數據類別進行區分,計算模型的精度,通過對比結果,時間序列分析AR(7)模型結果更加可靠、精確,充分利用時間序列分析的優越性挖掘數據之間的關聯性,盡可能準確預測數據類別,并對剩余壽命進行判斷,在實際生產中,可以充分挖掘數據之間的有關信息,為工業生產提供了更加準確的參考意見。
采用多組數據對模型進行訓練,并計算各個階數的模型誤差值,提高模型預測的準確率,是學術知識直接指導實際生產,實現科技轉化的項目;采用模型對壓力傳感器進行預測,解決工廠傳感器無法預知工作壽命的問題,更好地指導工廠生產。

