新型雙模式加權機制及其對網絡計算的影響*

李慧嘉 黃照詞 王文璇 夏承遺

1) (北京郵電大學理學院, 北京 100876)

2) (天津理工大學計算機與通信工程學院, 天津 300384)

高效率的網絡分析方法對于分析、預測和優化現實群體行為具有重要的作用, 而加權機制作為網絡重構化的重要方式, 在生物、工程和社會等各個領域都有極高的應用價值.雖然已經得到越來越多的關注, 但是現有加權方法數量還很少, 而且在不同拓撲類型和結構特性現實網絡中的效果和性能有待繼續提高.本文提出了一種新型的雙模式加權機制, 該方法充分利用網絡的全局和局部的重要拓撲屬性(例如節點度、介數中心性和緊密中心性), 并構建了兩種新型的運行模式: 一種是在原始模式中通過增加橋邊的權重來提高同步能力; 另一種是在逆模式中通過弱化橋邊的權重來提高聚類檢測.此外, 該加權機制僅受單一參數 α 的影響, 非常便于調控.在人工基準網絡和現實世界網絡中的實驗結果均驗證了該模型的有效性, 可以廣泛應用于大規模的現實世界網絡中.

1 引 言

復雜網絡理論[1?3]是一種分析大規模復雜系統的有力工具, 在過去十年里已經涌現出一系列相關研究成果, 例如聚類劃分技術、疾病傳播和免疫策略、交通驅動模型、同步分析、級聯失效、異常值搜索算法等等.在這些成果中, 拓撲計算和結構分析是研究復雜網絡內在特性的最有效途徑, 并使得理解網絡功能特征成為可能.其中, 最重要的拓撲特征之一是聚類結構[3?8].它在探測聚類時將節點分成若干子集, 子集之間應有清晰的邊界約束,同一組成員之間比不同組成員擁有更多的關聯.聚類信息有助于理解和分析網絡的結構特征和功能特性.

既有研究已提出了許多網絡聚類探測算法, 其中Newman等[9,10]提出的模塊度函數Q是最為常用的一種探測指標, 用以評價聚類劃分[2]的好壞.給定一個劃分Pk=(G1,G2,···,GK)=((V1,E1),(V2,E2),···,(VK,EK)), K是聚類的數目, 模塊度函數Q[9]定義如下:

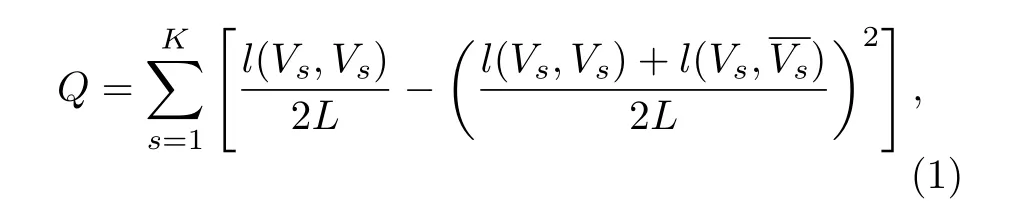
其中, L是網絡中邊的總數目, l (Vs,Vs) 和分別代表聚類s內部以及s與網絡中剩余部分之間的邊的數目.通常來說, Q值較大意味著該聚類結構較好[11?16].此外, Boccaletti等[17]根據網絡中的同步局域化理論提出了一種新的動態聚類檢測方法(opinion changing rate model, OCR).他們將改進的Kuramoto同步模型應用到網絡的每個節點中, 利用社團內部連接緊密而同步速度快的特征, 利用權重技術使得網絡聚類之間的邊權逐漸降低, 直到網絡聚類劃分獲得最大的模塊度Q值.復雜網絡中另一個廣泛存在的現象是同步[18?24].在連通網絡中, 每個節點通過網絡連接, 在動力系統的演化下, 與網絡其他節點進行耦合.在足夠強的耦合作用下, 節點的狀態會隨著時間的延長達到同步(狀態一致).在許多加權網絡中, 可以調整網絡的結構和權重, 以提升節點狀態獲得達到同步的能力.事實上, 已有研究結果表明, 在許多社會和生物網絡研究中, 同步行為會在調節系統和組織功能中發揮重要作用.

隨著數據收集技術的進步, 諸如互聯網、國際貿易網絡等現實網絡的規模極速增長, 如何處理這些大規模網絡已經成為巨大挑戰.傳統的指數型算法, 甚至是多項式時間算法, 也已難以適用于大規模網絡的計算與分析.為此, 研究人員可以嘗試另辟蹊徑, 如通過改變拓撲性質來提升網絡的計算效率.但是在許多實際應用中, 網絡結構通常是固定的, 一般不可能對邊進行重連.為了克服這一困難,可以為網絡連邊分配合適的權重, 用來異化不同屬性的邊, 以達到提升計算性能的目的, 如弱化類間邊的權重可以提高聚類探測的效率; 而在信息傳播研究中提高重負荷邊的流通負載(通常用權重表示)可以降低網絡擁塞.

當前, 加權方法已經得到越來越多的關注[21?30],但是總體來說數量還很少, 而且對于不同拓撲類型和結構特性的現實網絡, 特定加權算法的效果和性能仍不清楚, 還有待繼續分析和驗證.而且現有方法(在第2節詳細說明)通常僅利用一種節點中心度來定義網絡邊權, 對于結構相對均勻的網絡, 效果不理想; 而且對于相對稀疏的現實網絡, 調控參數的影響不明顯.另外, 目前加權之后的動態網絡中的各種隱藏特征, 如聚類結構和同步能力之間的相互關系, 仍未能得到很好的解釋和分析.

本文提出一種新型的雙模式加權機制, 用來解決上述問題.從一個簡單的無權無向網絡開始, 通過加權算法, 利用網絡的全局和多種局部信息(包括節點的介數、度、緊密中心度等), 將網絡轉化為能夠提高聚類和同步能力的加權有向網絡.這里的加權機制包括兩種模式: 在原始模式下, 它通過增加橋邊的權重以提高網絡的同步能力; 而在逆模式中, 則通過弱化橋邊權重以提高聚類的檢測效率.該加權機制只受一個參數 α 的控制, 可以很方便地進行調控.對于聚類探測, 通過在人工基準網絡(包括GN基準和LFR基準), 以及若干現實網上進行測試, 驗證了本文提出的加權機制不僅有助于提高探測精度, 而且還能緩解模塊度優化的分辨率限制問題.關于同步性, 通過在具有不同結構特性的無標度網絡和Watts-Strogatz網絡上進行測試,驗證了加權機制在提升網絡同步性能上的高效表現.通過比較, 本文提出的加權機制在提高網絡計算能力方面要優于其他以往發表的加權方法.

本文第1節和第2節分別梳理復雜網絡的基本理論及國內外相關的工作; 第3節引入本文使用的加權機制并提出對應的雙模式加權算法; 第4節對加權機制如何增強網絡同步性能及其對聚類結構探測的影響進行詳細分析; 第5節對加權機制分別運用于人工網絡和大量現實世界網絡進行試驗;第6節對全文進行總結, 并提出一些未來研究中值得深入考慮的問題.

2 相關工作

基于現實數據重構復雜網絡是了解和控制復雜系統的基本方式, 而作為網絡重構的重要組成部分, 網絡加權已經開始得到越來越多的關注.Chavez等[21]提出了一種通過拉普拉斯矩陣的非對角線元素 lij來增強同步能力的加權方案, 其加權后的元素定義如下:

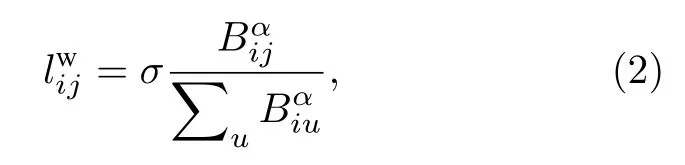
其中, α 為調控參數, Bij是節點i和j之間的邊介數中心度, α ≈1 相當于最優的同步能力.與之相似, Wang等[22]提出網絡可以被視為是加權無向網絡和加權有向網絡的疊加.基于現實網絡的特征, 他們假設了一個合適的梯度場, 并定義權重

如下:

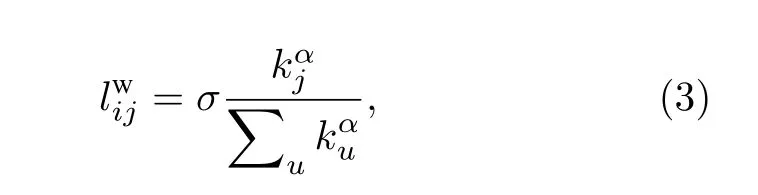
Charvez等和Wang等提出方法具有一定程度的相似性, 但后者利用的不是介數中心度, 而是基于節點的度.隨著 α 值的增大, 網絡同步化總是會隨之提升.然而, 同時應當注意避免 α 值過高, 否則會導致網絡斷開和分裂.為了解決這個問題, Jalili等[23]在節點介數中心度方法的基礎上提出了一種新的加權方法, 其中權重定義如下:

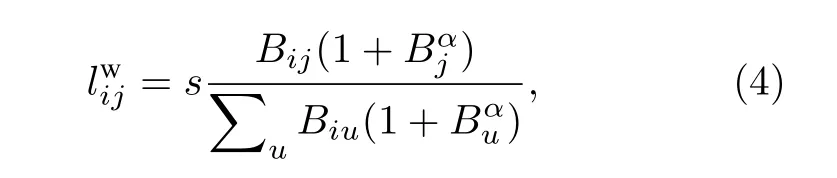
其中, BjB 和 BijB 分別代表節點j與邊 eij之間的介數中心度.該加權機制被用來提高網絡的同步性能.但是上述加權算法僅僅利用一種節點中心度來定義網絡邊權, 對于結構相對均勻的網絡, 效果不理想.而且對于相對稀疏的現實網絡, 調控參數的影響不明顯.

最近, Khadivi等[31]討論了一種新型加權機制, 用以緩解網絡聚類中的模塊度缺陷, 即分辨率極限[32]和極端限制[33]等問題.該加權機制利用了網絡的局部和全局信息, 其中每條邊的權重定義如下:

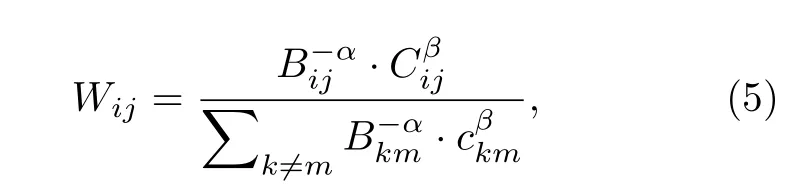
其中, cij定義為共同鄰居比例, Bij是邊介數中心度.利用Clauset-Newman-Moore方法[10]進行試驗, 驗證了該加權機制能夠顯著地優化社團探測的速度與精度.但是仿真分析也表明, 當網絡規模較小時, 其加權效果不明顯.而且雖然該方法可以用來加強社團內部的團內邊, 但是卻無法明顯降低團間邊的權重, 從而阻礙了該加權算法的進一步應用.另外現有的網絡加權方法還包括模擬退火算法[25]、文獻計量方法[26]、隨機游走算法[27]、級聯動力學方法[28]、變分貝葉斯方法[29]和概率推斷方法[30]等.但總體來說, 當前加權算法的數量還很少, 而且對于不同拓撲類型和結構特性的現實網絡, 特定加權算法的效果和性能仍不清楚, 還有待繼續分析和驗證.

3 復雜網絡基本理論

3.1 基本定義

假設 G (V,E) 是一個無向連通圖, V為節點集,E為邊界集.這里考慮三個最常用的衡量拓撲結構和信息流通的中心度指標.

節點度節點度 ki[34]表示節點i相連的邊的數量, 根據鄰接矩陣 A =(aij) 將其定義為

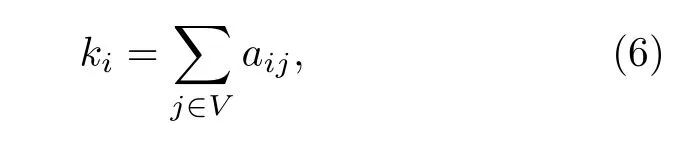
其中, aij是節點i和節點j之間的鄰接矩陣值.還可以將節點度擴展到加權網絡得到節點強度的概念.

節點強度節點強度 si[35]是節點i相關聯的邊的權重總和, 定義如下:

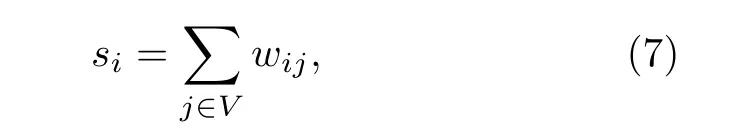
其中, wij為節點i和節點j之間的邊的權重值.

介數中心度一個節點在信息傳播中的重要性可以通過其介數中心度[36]來計算, 定義為

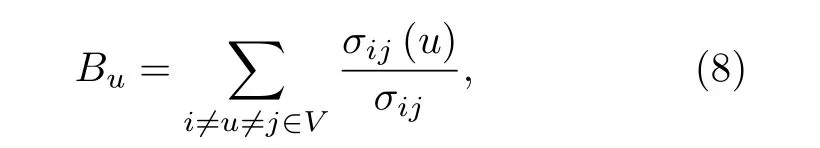
其中, σij(u) 為節點i和節點j之間的通過節點u的最短路徑的數量, σij是節點i和節點j之間的最短路徑的總數量.介數中心度的概念還可以拓展到邊.邊 eij的介數中心度 Bij表示通過該邊的最短路徑的數量, 在信息傳播研究中常用來表示流通負載.

緊密中心度(closeness)節點i的緊密中心度[36]定義為一個網絡中其他節點到節點i的平均距離的倒數

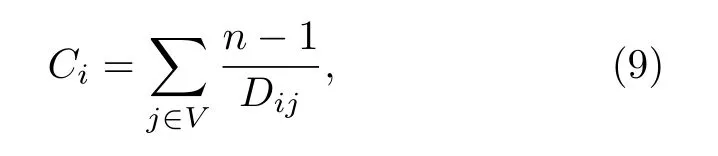
其中, Dij是節點i和節點j之間最短路徑的長度;Ci用來測量一個節點與其他節點的(平均)緊密程度.為了定義該中心性與最短路徑的直接(正比例)關系, 還可以將其定義為 Ci的倒數:

k-鄰域圖k-鄰域圖[37,38]定義為將節點i和節點j連接起來的最短路徑上的點的集合, 其中i和j之間的最短距離值小于等于k.由于鄰域關系是不對稱的( i →j ), 因此根據k-鄰域圖的定義得到的可能是一個有向子圖.在特定網絡中, 節點i的k-鄰域圖被構造為特定的相似性度量(這里指最短路徑距離)下顯示與i最相似的子圖.然而在大多數應用中, k的值難以直接給定, 以致其應用領域受到限制.

3.2 雙模式加權算法

1)通信鄰域圖

受到k-鄰域圖定義的啟發, 為了增強網絡信息流, 本文提出了一個新的拓撲定義——通信鄰域圖(communication neighbor graph, CNG), 并進一步提出一種新的加權算法.通信鄰域圖的具體定義如下.

通訊鄰域圖假設 G (V,E) 是一個無自循環的無向網絡, 其中節點的數量 | |V||=N.對于G中的節點來說, ζij是節點i與節點j之間的最短路徑(路徑為節點序列集合).節點i通過節點j的通信鄰域圖用 Πi→j表示, 其定義為: 給定節點u, 如果滿足通過節點i與u之間的最短路徑長度大于節點j與u之間的最短路徑長度, 即 l (ζiu)> l (ζju) ,那么節點u屬于 Πi→j.如果節點i和節點u之間存在一條以上的最短路徑, 那么就認為 ζiu是其中任意一條.根據通信鄰域圖CNG的定義, 對于特定節點u, 假定節點i與節點u之間有邊相連, 如果 ζiu經過節點j, 那么節點u就屬于 Πi→j.

注意到通信鄰域圖CNG是非對稱的, 即一般情況下 Πi→j與 Πj→i是不同的.對于任意一對相鄰的節點i和j來說, 節點j一定屬于 Πi→j.另外, 任一節點屬于且僅屬于節點i的一個通訊鄰域圖.圖1(a)給出了兩個相鄰節點的通信鄰域圖的例子.當網絡是稠密且規模不大時, 該定義是非常直觀的.

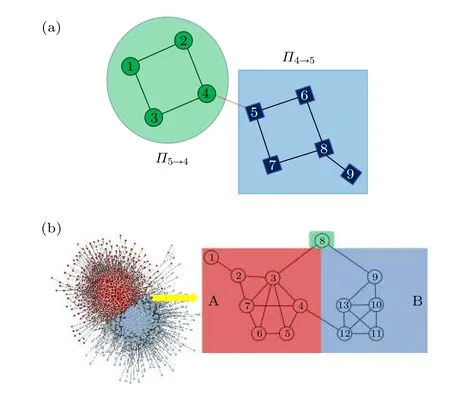
圖1 (a)節點4和節點5之間邊對應的通訊鄰域圖; (b)網絡中的橋邊Fig.1.(a) Communication neighborhood graph corresponding to the edge between node 4 and node 5; (b) bridge side in the network.

2) 加權算法

如果邊權與流量成正比, 那么為了增強連邊上的信息流, 需要研究最有可能出現瓶頸的橋點和橋邊.因為橋點和橋邊數目較少且處于兩個類之間,它們往往無法承載端點需要發送的全部信息, 如圖1(b)所示.如果節點具有大的度、介數中心性和緊密中心性, 那么它更有可能具有高信息吞吐量,因此這些節點及其所連的邊更可能成為瓶頸.在本文模型中, 這種可能性被假設為與單一實數成正比, 即定義圖中每個節點的 γ 值.

在給定通信鄰域圖CNG的定義后, 接下來介紹一種新型的加權機制.令 γ (u)∈R 表示屬于Πi→j中節點u的一個特定指標,Γ(Πi→j)={γ(u1),γ(u2),···,γ(uk)} 且 是 Πi→j中 所 有 節 點 的 γ 值集合, 其中 u ∈Πi→j.那么, 本文的加權機制定義如下:

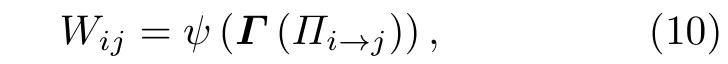
其中, ψ 為任意實數集中的單一實數相關的函數.這是一種具有代表性的加權方法, 可以用來加強與網絡通信相關的多種計算與應用.

本文加權算法旨在重點增強瓶頸節點的各種中心性值, 使其與加權權重成正比, 以便增強網絡的整體通信能力.定義 ψ 為一個集合所有元素的加和, 即如果 X ={x1,x2,···,xN} , 那么ψ(X)=定義節點u的加權參數為

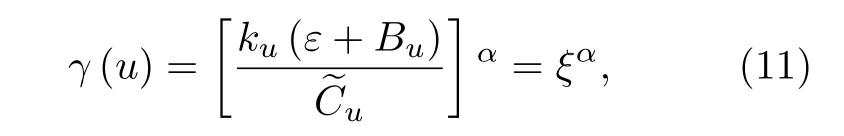
其中, α ∈R , 且 ku, Bu和分別為網絡G中節點的度、介數中心性和緊密中心度 Cu的倒數.ε 設定為0.01, 以避免 γ 值為0.設計加權參數 γ 是為了反映瓶頸節點u的各項參數, 包括度 ku, 介數中心性 Bu和緊密中心度 Cu, 如果各項參數比較大, 則γ也比較大, 節點u成為瓶頸節點的概率也會很大.那么, 節點j到節點i的權重為

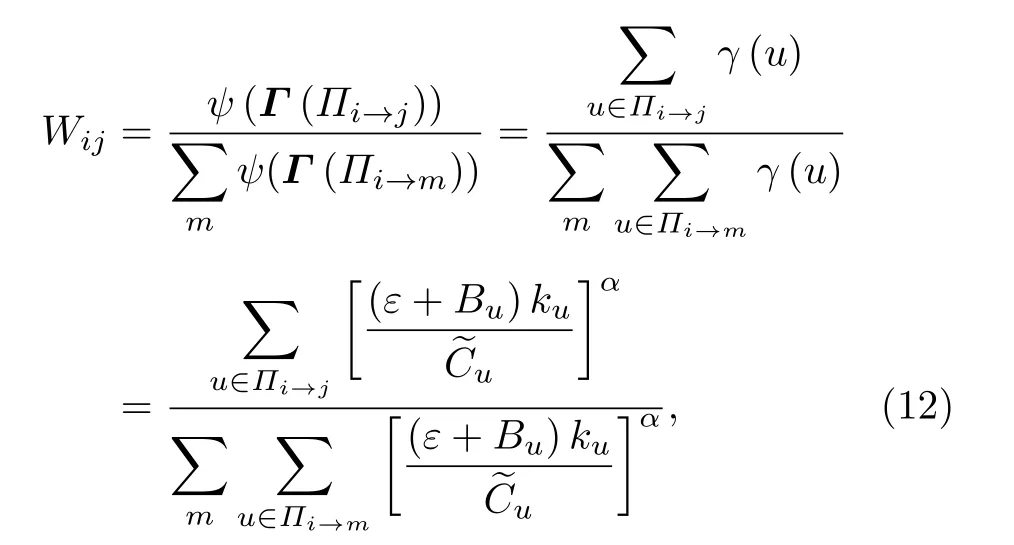
其中 Πi→j表示節點i通過節點j的通信鄰域圖.(12) 式表示的加權機制的原理為當傳輸線路i→j 比較重要時, 其通信鄰域圖 Πi→j的規模也會 相 應 比 較 大.則 當 α >0 時, (12)式 的 分 子 項和相應的權重 Wij也會相應比較大,從而實現了加權機制增強重要通信邊的權重的目的.這里, 分母項的設置是為了實現標準化, 權重矩陣的對角線元素被設置具有零行和屬性, 即

在加權策略((12)式)中, 分母的標準化項使得入度更加均勻.另外, γ 函數((11)式)增強了以高 γ 值節點為起點的路徑, 并且進一步使得網絡流量更加趨向于流向這類節點.這個過程使節點的負載分配更加傾向于平均.總而言之, 本文提出的加權策略使負載分布更加均勻化, 同時降低了平均路徑長度.本文加權算法具體流程如算法1所示.本算法由于需要計算節點的介數、度、緊密度三種中心性度量, 時間復雜度分別為O(n3), O(n2)和O(n3), 因此總的時間復雜度為O(n3).

算法1網絡加權算法流程

輸入: 網絡G, 其節點數為n, 邊數為m; 加權參數α.

輸出: 網絡加權矩陣W.

1） 根據“通訊鄰域圖”的定義計算網絡中每條邊的通訊鄰域圖;

2） 計算 ku, Bu和 C ～u, 分別為網絡G中節點的度、介數中心性和緊密中心度 Cu的倒數;

3） 根據(6)式和(11)式計算節點u的加權值γ(u);

4）根據(12)式更新網絡中邊的加權值wij.

需要說明的是, 本文提出的加權機制是使用虛擬方式改變拓撲結構, 但是僅通過加權來達到網絡重連的效果是不大可能的.例如, 在環形規則網絡中, 所有節點的 γ 值是相等的, 加權機制并不能增強網絡的傳輸容量.因此, 本文的加權機制旨在通過降低瓶頸節點的限制, 使網絡層次結構趨于平坦以提高傳輸容量.這種加權機制對具有非均勻層次結構和瓶頸節點的網絡(如無標度網絡)來說很有效率.反之, 均勻網絡或無瓶頸節點的網絡則不具備這種加權機制的優勢.此外, 本文的加權策略還有一個重要優點: 只受一個參數調控, 即參數 α , 可以用來控制加權權重的異質程度(即非均勻性).這里有三種典型的情況:

當 α >0(α<0) , 在通信鄰域圖中, 具有高ξ值的節點對信息傳輸會有更多(更少)的貢獻.特別地, 在同質(均勻)網絡中, 節點呈現出均勻的負載和度分布, 那么節點的 ξ 值和隨之得到的加權值也會變得均勻.在這種情況下, 改變 α 不會導致權重和網絡傳輸效率發生顯著變化.類似地, 當網絡負載分布和度分布是異質(非均勻)時, 不同的 α 會導致權重和網絡傳輸效率發生顯著變化.因此, 在異質(同質)網絡中, α 會有更多(更少)的影響.

當 α =0 時, γ 值將退化為對所有節點u都有γ(u)=1.值得注意的是, 這種情況與無權網絡或者標準化僅僅應用于節點度的情況不同.在這種情況下, 僅考慮每個通信鄰域圖的節點數量, 它在γ值分布的方差較小的網絡中將會相當有效, 即 γ 值的同質性.

由于受標準化因子和通信鄰域圖節點數目的影響, α <0 并不會產生負值, 但是會使得信息傳輸能力下降(即具有高 ξ 值的節點對信息傳輸會有更少的貢獻).根據本文框架, 我們提出了利用轉置權重矩陣以降低傳輸能力的逆加權方案.為了能夠更方便地轉換, 權重矩陣被定義為

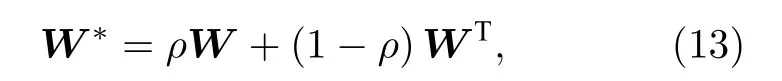
其中, 參數 0 ≤ρ≤1 , 表示傳輸程度.例如, 當ρ=1 意味著高傳輸流量, 而 ρ =0 意味著低傳輸流量.

逆模式加權機制在(12)式的加權機制中,設定參數 α <0 , 定義為逆模式加權機制.根據(12)式, 在逆模式加權機制中, 即具有高 ξ 值的節點對信息傳輸會有更少的貢獻, 從而會使得網絡流量更加趨向于避開這類節點, 使得信息傳輸能力下降.為了能夠更方便地轉換, 權重矩陣被定義為(13)式.逆模式加權算法如算法2所示.

算法2逆模式加權算法流程

輸入: 網絡G, 其節點數為n, 邊數為m; 加權參數 α <0 ; 傳輸程度參數0≤ρ≤1.

輸出: 網絡加權矩陣W.

1) 根據“通訊鄰域圖”的定義計算網絡中每條邊的通訊鄰域圖;

2) 根據(11)式計算節點u的加權值 γ (u) ;

為了測試參數 α 的影響, 將其應用到著名的BA網絡中, 分別考慮 α =2 和 α =6 兩種情況, 結果如圖2所示.可以看出, 受加權機制的影響, 節點強度和節點度會出現明顯異化.此外, 當α=6時, 節點強度和節點度的關系的分布相較于α=2時更加分散.這是因為 α 的值越大, 更多的邊會得到較大的權重值.該結果與前面加權機制的分析相符合.因此, 通過本文的加權策略, 權重分布、節點強度以及度的關系均依賴于參數 α 的值, 該加權網絡比相應的二進制無權網絡提供了更多的信息.

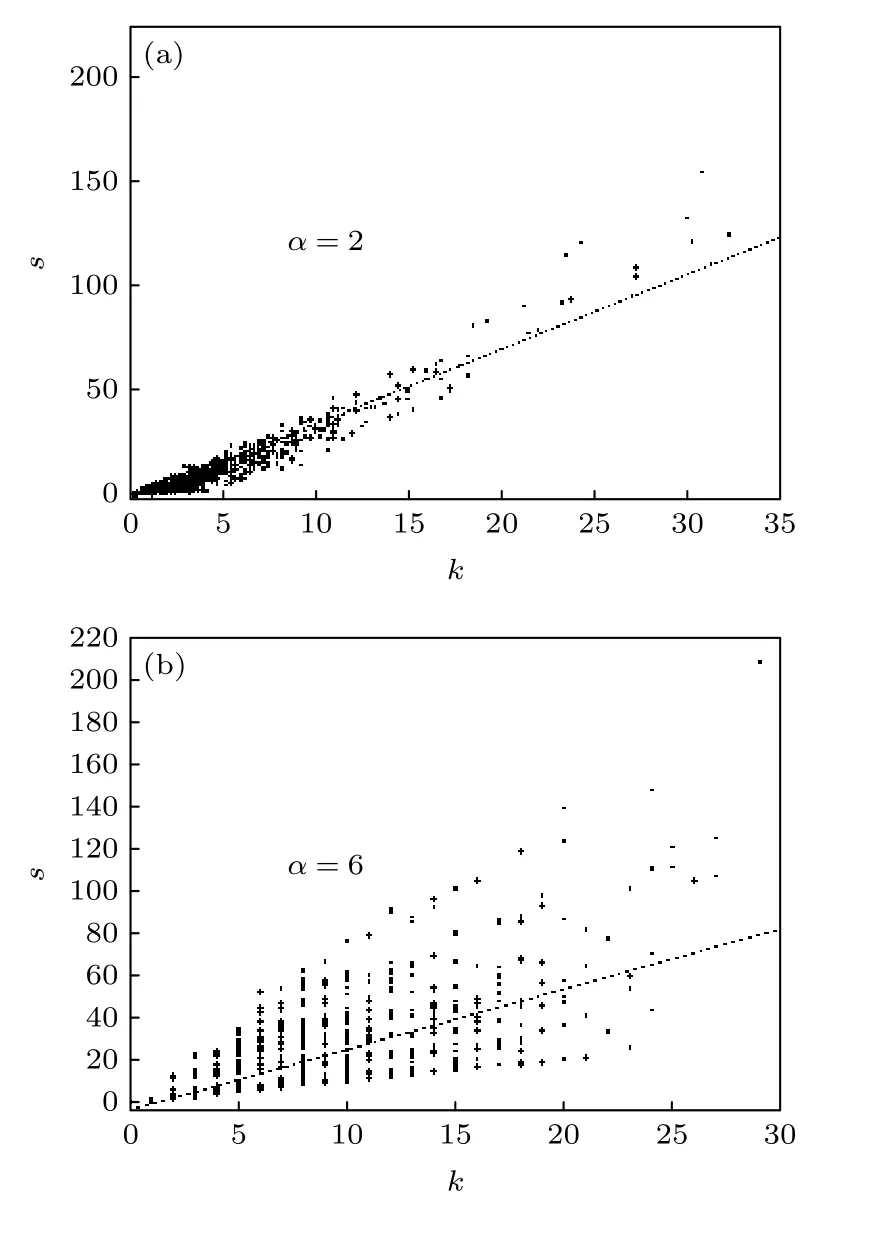
圖2 參數α取不同值時BA模型中節點強度s和節點度k之間的關系(N = 5000) (a) α =2 ; (b)α=6Fig.2.Relationship between node strength s and node degree k in BA model (N = 5000) with different values of parameter α: (a) α =2 ; (b) α =6.

4 復雜網絡的屬性分析

許多研究[20,39,40]發現, 網絡中信息傳輸的難易程度可以解釋為同步能力, 并且它們都被網絡拓撲矩陣的特征值所限制.由此直接引出本文提出的加權方案, 它可以試圖通過改善信息流以增強同步能力.然而, 并不是所有的應用都需要提高同步能力,有些反而需要降低, 比如降低網絡的同步性有助于辨別網絡中的聚類結構[17].本節將分析加權機制對網絡同步能力的作用, 并進一步分析其對聚類探測及其效率的影響, 從而有效驗證加權機制的高效性.除了同步和聚類分析, 本文加權機制還可以有效應用于網絡流行病傳播關鍵路徑識別、免疫策略分析、演化博弈分析、路由策略設計、交通擁塞預防等多個方面.

4.1 同步性分析

首先說明加權機制增強網絡同步性能的原因.設 λ1≤λ2≤,···,≤λN為加權矩陣W的N個特征值.根據文獻[41], 矩陣W的特征值比 λN/λ2越小, 則意味著該網絡具有更大的同步能力.如上所述, 網絡通信的能力可以被解釋為在網絡中信息流動的難易程度.更確切地說, 可以將動態方程寫作:

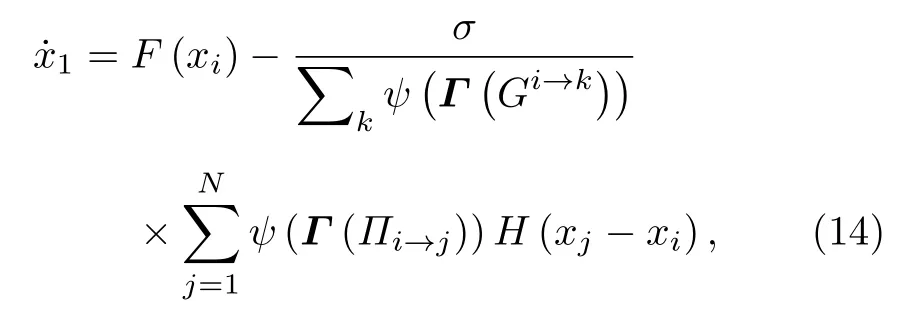
通過網絡加權, 總是可以將W的對角線元素標準化為1, 從而防止任意大或者任意小的耦合值.權重矩陣W是不對稱的, 并且一般而言非對稱矩陣的特征值非常復雜.下面的推論證明了非對稱矩陣W具有有界的實數特征值.

推論1加權機制((12)式)得到的權重矩陣的所有特征值是實數, 且值介于0—2之間.

證明權重矩陣W對應的拉普拉斯矩陣 Lw,寫作 Lw=MQ , 其中

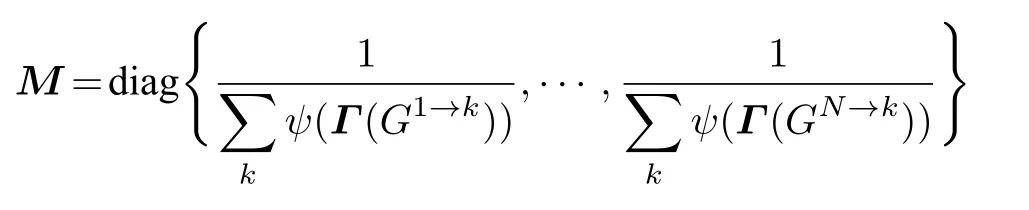
Q是一個零行和矩陣, 具有負非對角項, 即Qij=?ψ(Γ(Πi→j)).容易看出, W的特征值λi(i=1,···,N) 與 M1/2QM1/2的特征值相等, 即是實數且非負的, 且最小特征值 λ1=0.另一方面,Gerschgorin循環定理[42]證明了 Lw的每個特征值都在一個半徑為1的圓的內部, 因此0=λ1≤λ2≤,···,≤λN≤2.證明完畢.

接下來引入超中心節點的定義.

超中心節點網絡中具有最大 γ 值的節點被稱為網絡的超中心節點.

定理1令 G (V,E) 為一個無向網絡, 對于每一對節點u和v, 選擇它們之間的最短路徑 S Puv, 并根據通信鄰域圖的定義確定通信鄰域圖運用加權機制((12)式).如果該鄰域圖具有唯一的超中心節點, 那么當 α →+∞ 時, 通過移除超中心節點的輸入邊, 剩余網絡將會退化到一個以超中心節點為根節點的有向生成樹, 因此總有一條有向路徑可以從超中心節點通向其他所有節點.

證明根據(12)式, 當 α →+∞ 時, 可以得到ψ(Γ(Πi→j))≈max{Γ(Πi→j)} , 從而有現在, 假設節點 u?是唯一的超中心節點, 即網絡中具有最大的 γ 值的節點.當 α →+∞ 時, 如果 u?∈Πi→j并收斂于0, 權重 Wij將收斂于1.換言之, 每個節點?只保持一條邊連接網絡中具有最大 γ 值的那個節點.由于 u?的輸入邊被刪除了, 也就是所有到u?的輸入邊的權重都等于0, 僅保留N – 1條有向邊.因此, 從節點 u?到網絡中所有其他節點都有一條有向路徑, 且僅保留有N – 1條邊, 由此得到的網絡結構是一個有向生成樹, 其中具有最大 γ 值的節點是根節點.證明完畢.

推論2根據參考文獻[41], 定理1中得到的有向生成樹的特征值比 λN/λ2=1 , 意味著該網絡具有最大的同步能力.簡單來說, 由于生成樹的根擁有最大的 γ 值, 因此在所得的生成樹中, 大多數節點都在樹的較低層次上, 也就是說大多數節點與根節點的平均距離較短.值得一提的是, 當α→+∞時, 如果不移除根節點的輸入邊, 那么特征 值 比 λN/λ2=2 , 也就是說,0=λ1<λ2=λ3,···,=λN?1<λN=2.如果超中心節點并不唯一, 當 α →+∞ 時, 網絡將退化為有向圖, 其中所有超中心節點都屬于邊權重相等的團.此外, 該團中的任意節點都能與圖中的所有其他節點相連, 即對于網絡中的每個節點來說, 都有一條有向路徑通向每個超中心節點.基于上述可以發現, 只有參與這些路徑的邊被留下來, 而其他的邊都將會消失.

4.2 聚類結構分析

前文已經提到, 在一些應用中, 有時候還需要降低同步能力, 如辨別網絡中的聚類結構[17].本文提出的加權策略對聚類結構探測也有很強的影響,并且可以進一步發現聚類結構與同步性之間的隱藏關系.首先給出聚類結構的弱定義:

聚類結構的弱定義Radicchi等[43]分別從弱定義和強定義這兩方面給出了衡量聚類結構的量化標準, 其中弱定義被認為是一個子圖集合能夠成為聚類結構的最弱標準, 即聚類是網絡的子圖集合, 子圖內部的邊的密度高于子圖之間的邊的密度.給定一個網絡 G =(V,E) , 其中V是節點集,E是邊界集, A =(aij) 為 其鄰接矩陣, 令Vs?V為一個特定子圖, Vs=VVs為網絡其余的節點集,那么在弱靈敏度條件下 Vs能夠成為一個聚類的條件是:

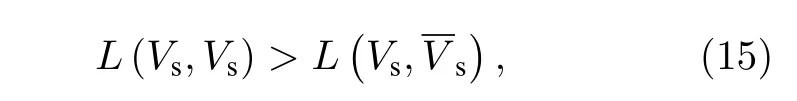
推論3如果 eij是一個類間邊, 那么鄰域圖Πi→j和 Πj→i很可能是兩個相鄰的聚類.此外, 在極端情況下, 如果網絡是二劃分且 eij是唯一的類間邊, 根據聚類結構的弱定義, Πi→j和 Πj→i將是嚴格的網絡聚類.

證明:根據弱定義, 如果一個網絡擁有聚類結構, 由于存在高密度的類內邊, 一個隨機游走者將會在一個聚類中停留很多的時間.這意味著一個節點到同一聚類內的節點的路徑長度通常比到不同聚類的節點的路徑長度短.如圖2中 α =2 時,Πi→j中的節點到節點j的路徑長度比到節點i的路徑長度都要長.相反, Πj→i中的節點到節點i的路徑長度比到節點j的路徑長度長.因此可以得出結論: Πi→j和 Πj→i很可能是兩個不同的聚類.此外, 如果 eij是唯一的類間界, 根據聚類結構的弱定義, 這個結論是嚴格的.證明完畢.

為了闡明加權機制對聚類結構的影響, 逐步增大 α 的值并在示例網絡中刪除 Wij<0.5 的 邊.如圖3所示, 當 α 值從2增加到4, 聚類結構會顯著增強.

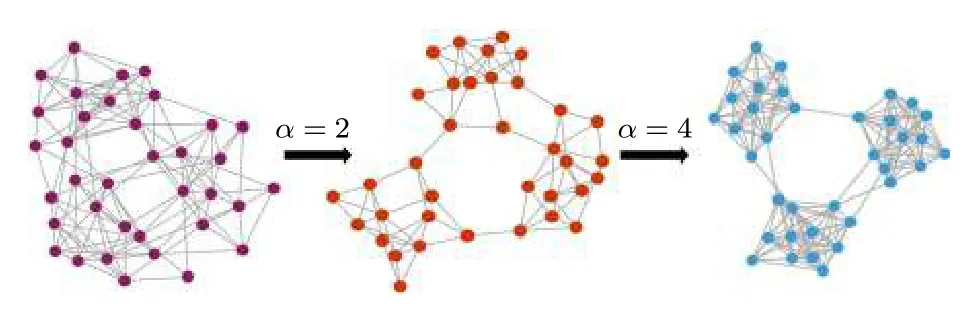
圖3 應用加權機制后網絡的動態演化示例圖Fig.3.Example of dynamic evolution of network after applying weighting mechanism.

根據弱定義, 比率 R =lout/lin在解決模塊度優化問題上發揮著十分重要的作用.為了滿足弱定義的標準, 這個比率的區間應該為[0, 2].

定理2令 lout為類間邊的數量, lin為類內邊的數量, 那么比率 R =lout/lin可以用來有效量化網絡中的聚類結構.

證明對于特定的網絡G, 其相對的超圖G?定義為一個有向加權的C團結構, 其中的每個節點對應于G的一個聚類.在 G?中, 節點r和節點s之間的邊用來加權, 其中代表G中聚類r和聚類s之間的團間邊數量,代表聚類r內部邊的數量.G?對應的 C ×C 拉普拉斯矩陣F={Frs} 是不對稱的, 但是可以變換為 F =?Θ , 其中?={?rs}是一個對稱的零行和矩陣, 其非對角元素為對角元素為且那么可以將F寫成:

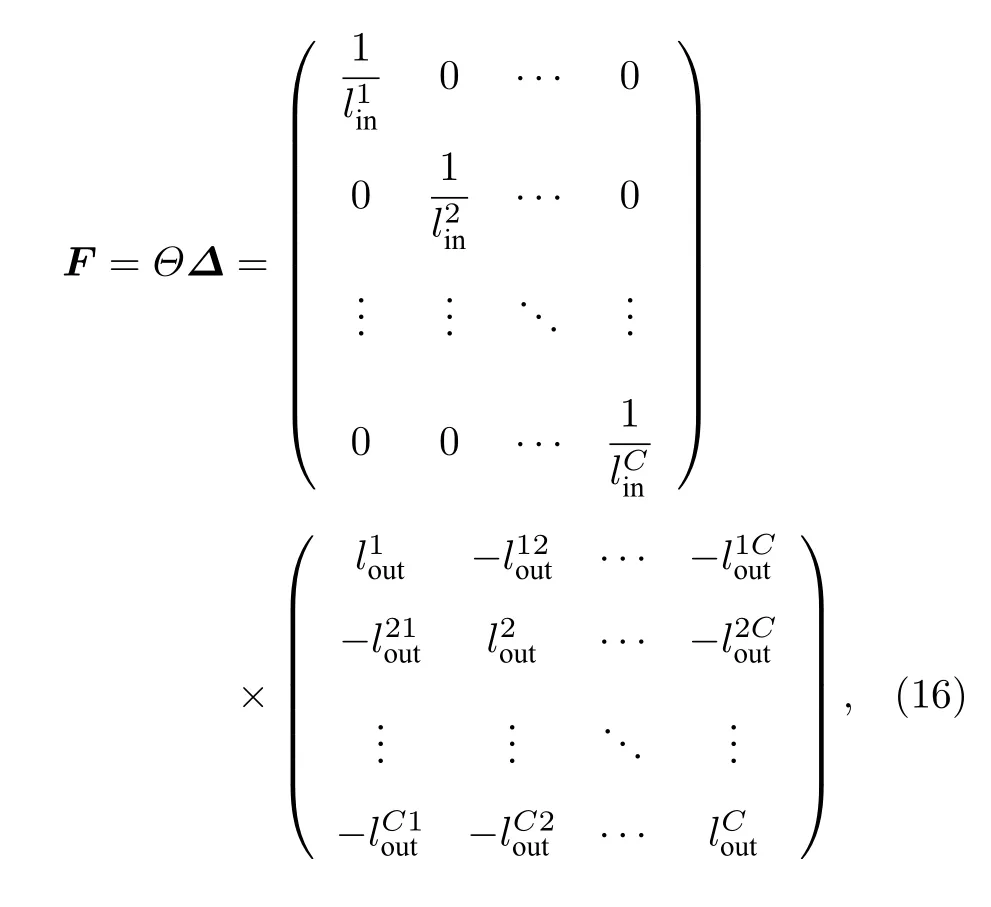
因為F是零行和的, 所以F的譜元素都是非負實數, 其中F的最小特征值, 次小特征值

根據譜方法和信息論[42,44?46],能夠量化超圖的連通性, 從而衡量不同聚類的性質和互相關聯的程度.應該注意到,已經過標準化, 所以它應該是一維的.這里, 可以得出.特殊情況下, 如果C個聚類都具有相等規模 Nc=N/C ,那么類內邊數量和類間邊數量對所有聚類來說都是一樣的.此時, 由和可以得到由?=CI/lin, 可以得到證明完畢.

接下來將展示本文的加權策略如何化解聚類探測中的分辨率限制問題, 以使優化方法更加有效.Fortunato和Barthelemy[32]發現了聚類探測的分辨率限制問題, 表明對于優化模塊度Q((1)式)的算法, 如果的取值區間不在[0, L]內, 那么模塊度優化算法將無法檢測到這些聚類.直觀地看, 如果引入一種加權策略, 能夠有效擴大這個限制區間, 那么許多優化算法就能夠在一個較大的限制范圍內探測到準確聚類.為了分析簡便, 假設權重之和邊的個數L保持相等.這里, 加權網絡中所有的量都以上尖號為區分, 即.首先, 回顧一個關于聚類規模邊界的定理[32].

定理3聚類規模對模塊度函數Q的影響有如下限制:

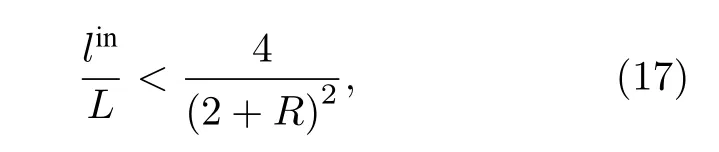
其中, R =lout/lin.如果合并聚類i和聚類j不能提高模塊度函數Q的值, 那么對于聚類i和聚類j的規模有如下約束條件[31]:

對所有j, 有

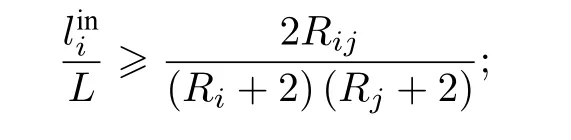
對所有i, 有

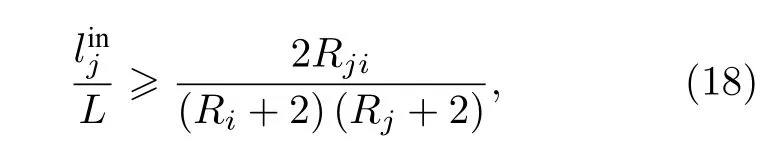
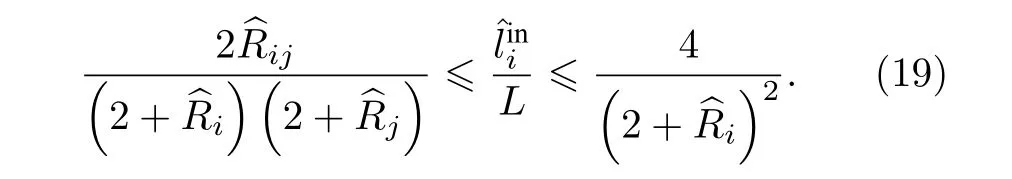
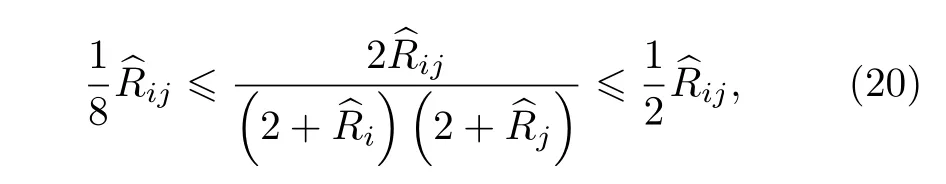
總結來說, 如果將本文的加權策略應用于網絡中, 那么能夠通過優化算法探測出更大或更小的聚類, 從而可以有效地降低分辨率限制的問題.

5 實 驗

本節將上述加權機制運用在人工網絡和大量現實世界網絡中.結果表明, 這種加權機制可以分別利用原模式和逆模式來提高網絡同步能力以及增強聚類結構檢測能力.

5.1 同步性

在本文提出的加權策略中, 唯一的調整參數是α.通過改變 α 參數, 可以控制權重值的異質性和特征值比 λN/λ2.

1)人工基準網絡

這里利用無標度網絡[2]和Watts-Strogatz小世界網絡[1]作為基準模型網絡, 并將本文加權機制應用其中.無標度網絡的節點度分布服從冪律特性, 即該模型有兩個參數, 其中節點初始邊數 k0控制平均度, 即 〈 k〉≈2k0.另外, 參數 β 調整控制網絡度分布的異質性, 當 β 增加時, 網絡的異質性會減少到特定程度.

圖4給出了在無標度網絡上的實驗結果, 其中數據點為50次實驗結果的平均值.圖4(a)為特征值比 λN/λ2和參數( α , 〈 k〉 )的對應關系, 這里網絡的平均度用 〈 k〉 表示.設 α =1 , 對于所有的平均度〈k〉 , 可以得到 λN/λ2<2 , 這比文獻[23]的最優情況還要好, 而又優于文獻[21, 22, 39]的研究結果.對于較大的平均度 〈 k〉 , 權重分布和度分布的同質性增加, 這表示 γ 值將更加均勻, 而 α 的影響也會較弱.所以, 無論 α 的大小, 加權過程都將顯著提高網絡同步能力.對于平均度 〈 k〉 較低的網絡, 由于網絡中異質性較高, 因此較大的 α 將會得到更好的結果.接下來研究網絡的異質性(非均勻性), 該性質可以用參數 β 來衡量.已有研究表明, 網絡度分布的異質性是影響同步性能最重要的因素之一.無標度網絡中特征值比 λN/λ2和參數 α , β 的關系如圖4(b)所示.對于不同的 β , 因為無標度特征導致節點度的非均勻性, 參數 α 的影響作用會更加顯著.此外可以看出, 隨著 β 值增加, 網絡非均勻性降低,得到的加權網絡的同步性會逐漸變差.

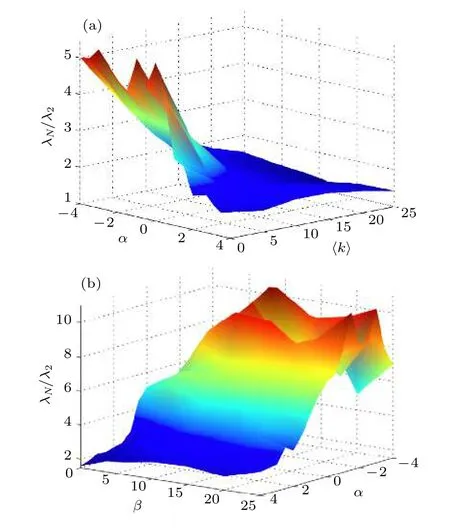
圖4 (a) 無標度網絡中 λ N/λ2 與( α , 〈 k〉 )的對應關系(N = 500, β =0 ); (b)無標度網絡中 λ N/λ2 與( α , β )的對應關系(N = 500, 〈 k〉=4 )Fig.4.(a) Corresponding relationship (N = 500, β =0 ) in scale-free networks between λ N/λ2 and ( α , 〈 k〉 ); (b) Corresponding relationship (N = 500, 〈 k〉=4 ) in scale-free networks between λ N/λ2 and ( α , β ).

接下來將加權機制應用到Watts-Strogatz網絡中, 相對于無標度網絡來說, Watts-Strogatz網絡的節點度分布是均勻的.該網絡受兩個參數控制, 即平均度 〈 k〉=2k0, 和重連概率P.圖5給出了在Watts-Strogatz網絡中應用本文加權算法的結果, 圖中數據點為50次實驗結果的平均值.其中, 圖5(a)為特征值比 λN/λ2隨參數 α 和網絡平均度 〈 k〉 的變化情況.和無標度網絡相似, 當平均度〈k〉 增加時, 網絡的異構程度隨之降低 α , 從而降低α的貢獻程度.可以看出, 當平均度 〈 k〉 非常高時,α對特征值比 λN/λ2幾乎沒有影響.圖5(b)為特征值比 λN/λ2隨參數 α 和重連概率P的變化情況.當P較小時, 網絡度分布幾乎是均勻的, 但是節點的負載分布卻是極度非均勻的.這是由于極少數的重連邊可以被視作捷徑, 它們承擔著很高的負載,導致負載的分布具有高度的不均勻性.隨著重連概率P的增加, 網絡重連邊的數量會逐漸增加, 負載分布會因此變得越來越均勻.在這種情況下, 雖然度分布的方差會逐漸增加, 但仍不足以提升 γ 值的異質程度.因此, 增加P會使 γ 值分布更加均勻,從而降低加權機制的貢獻程度.特別地, 當P = 1時, Watts-Strogatz網絡等同于完全隨機圖.

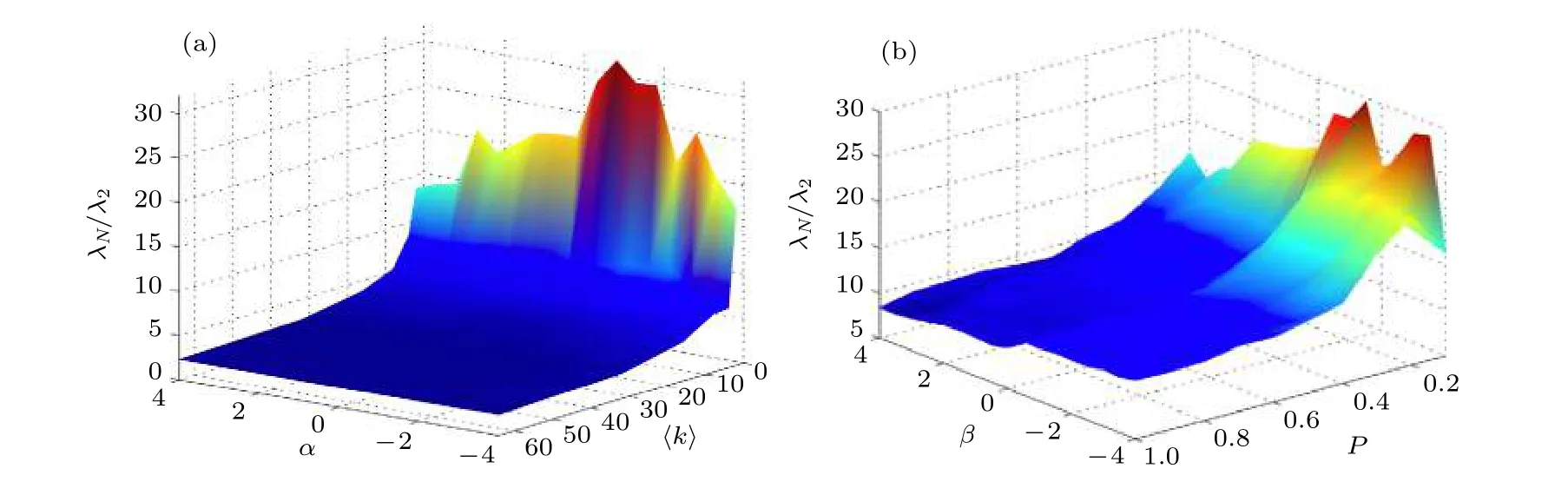
圖5 (a) Watts-Strogatz網 絡 中 λ N/λ2 與( α , 〈 k〉 )的 對 應 關 系(N = 500, P = 0.1); (b) Watts-Strogatz網 絡 中λN/λ2與( α , P)的對應關系(N = 500, 〈 k〉=4 )Fig.5.(a) Corresponding relationship (N = 500, P = 0.1) in Watts-Strogatz networks between λ N/λ2 and ( α , 〈 k〉 ); (b) corresponding relationship (N = 500, 〈 k〉=4 ) in Watts-Strogatz networks between λ N/λ2 and ( α , P).

2) 現實世界網絡

雖然現實世界極其復雜以致無法獲取全部信息, 但是為了充分地進行驗證, 我們將9個不同的加權機制應用到大量現實世界網絡中并進行對比,包括Chavez方法[21]、Wang方法[22]、Jalili方法[23]、Khadivi方法[31]、模擬退火(SA)算法[25]、隨機游走(RW)算法[27]、變分貝葉斯(VB)算法[29]、概率推斷(PL)方法[30]和本文方法, 結果列在表1中,其中設定 α =4.可以看出, 本文使用的加權機制的性能超過了其他所有的加權方法.值得一提的是, 對于所有的現實世界網絡, 隨著 α 的增加, 特征值 λN/λ2比都將收斂于2.

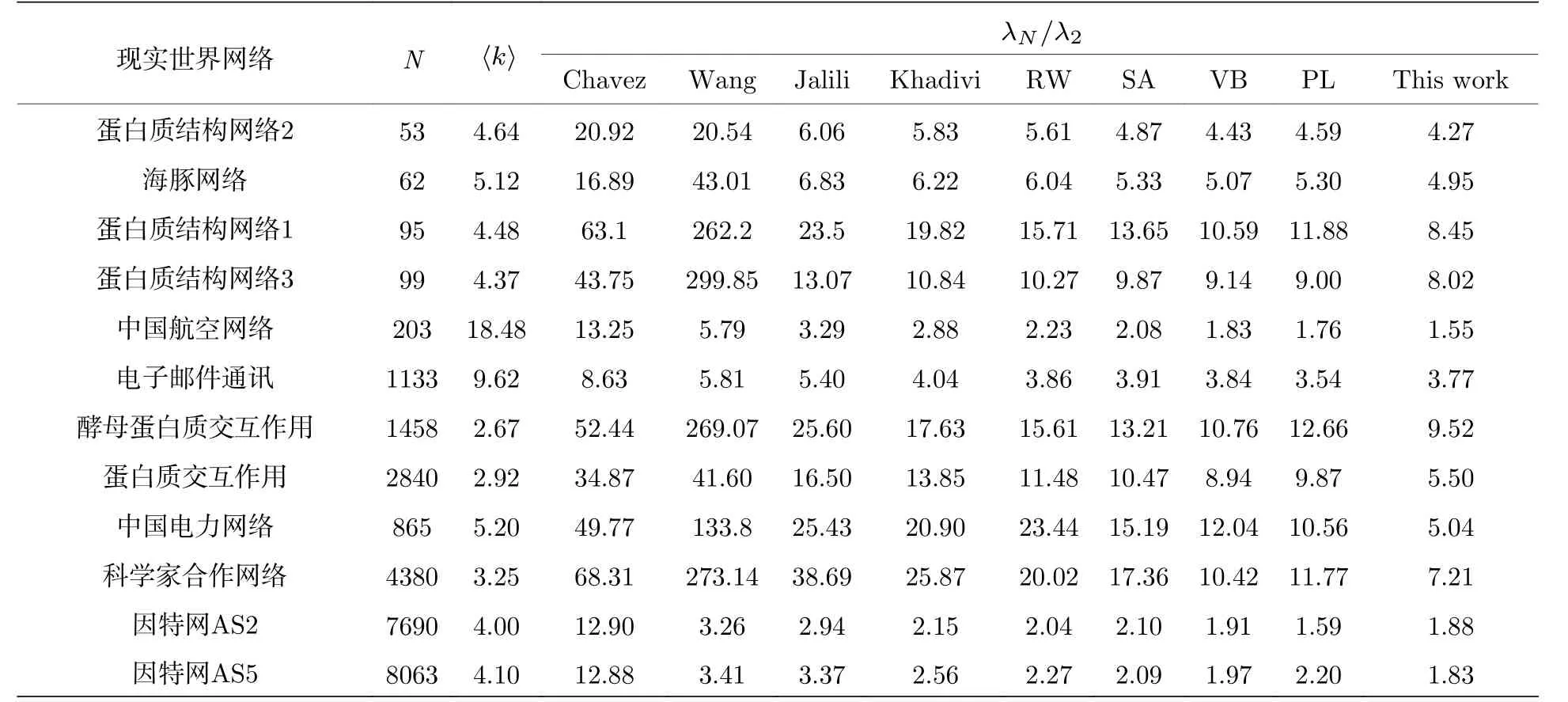
表1 在現實世界網絡中使用8種不同加權策略的實驗結果對比, 其中RW代表隨機游走方法, SA代表模擬退火方法,VB代表變分貝葉斯方法, PL代表概率推斷方法Table 1.Comparison of experimental results using eight different weighting strategies in real world networks, in which RW represents random walk method, SA stands for simulated annealing method, VB stands for variational Bayesian method, PL stands for probability inference method.

5.2 聚類探測

1)人工基準網絡

本文采用兩個著名的人工基準網絡, 即Girvan-Newman (GN)基準網絡和Lancichinetti-Fortunato-Radicchi (LFR)基準網絡, 用以評估加權機制對社區探測效率的影響.其中, GN基準測試[9,11]已經廣泛應用于對不同聚類算法的效率評估.GN網絡共包括128個節點, 這些節點被分配到4個聚類中, 每個聚類包含32個節點, 每個聚類內部點之間連邊和與類外節點連邊的概率分別為 pin和 pout.因此, 對于每個節點, 它們在聚類內部的邊的個數和與其他類節點關聯的邊的期望分別為 zin=31pin和 zout=96pout, 可以看出 zin+zout=16.

更進一步地, Lancichinetti等[47]提出了LFR基準網絡, 它可以通過調整相關參數來符合現實網絡中的無標度特征.在該基準網絡中, 節點的度分布和聚類規模遵循冪律分布.此外, 還需要設定一些其他參數, 包括節點最大度、節點平均度、節點總數、聚類最大規模和最小規模以及最重要的混合參數 μ.混合參數 μ 的取值區間為[0, 1], 決定了LFR基準圖的聚類模糊性程度: μ 越大, 聚類就越難被正確劃分.可以看出, GN基準網絡是LFR基準網絡的一個特例.由于GN基準網絡和LFR基準網絡的社團都是預先給定的, 而不同劃分算法得到的結果是不同的, 因此這里利用正確率R(正確劃分的節點和全部節點的比值)衡量劃分的正確性.

首先, 將加權策略將應用于GN基準網絡.在圖6(a)的原加權網絡中, α 取2和4, 在逆加權網絡中, α 取–2和–4, 數據點為50次實驗結果的平均值.圖6(a)給出了在GN基準網絡上應用加權策略前后的平均正確率R的對比.可以看出, 當α=4 和 α =2 時, 加權策略的原模式都提高了平均正確率R, 而相應的兩個逆模式 ( α =?4 和α=?2 )都會降低平均正確率R.與 α =4 的情況相比, 在 α =2 的情況下, 平均正確率R會下降約2—3倍.而且在逆模式中, 當 zout≤6.5 時,α=?4的情況與 α =?2 相比, 平均正確率R會降低2倍以上.

其次, 在LFR基準網絡上進行分析, 其中參數設置如下: 節點數量為1000、平均度為20、最大節點度為50、冪律分布指數為2、混合參數 μ 在區間[0, 0.5]內變化.從圖6(b)可以看出, 加權策略的原模式會顯著提高平均正確率R, 而相應的逆模式會降低平均正確率R.與 α =4 的情況相比, 在α=2的情況下, 平均正確率R會下降約4—5倍.另外, 在逆加權模式也會得到相似的結果.比較兩種基準網絡, 對于提高平均正確率R, 加權策略在LFR基準網絡中會取得更好的效果.

圖6 (a) GN基準網絡中使用加權機制(逆加權機制)前后平均比率R的對比; (b) LFR基準網絡中使用加權機制(逆加權機制)前后平均比率R的對比Fig.6.(a) Comparison of average ratio R before and after using weighting mechanism (inverse weighting mechanism)in GN benchmark network; (b) comparison of average ratio R before and after using weighting mechanism (inverse weighting mechanism) in LFR benchmark network.

再次, 為了展示加權機制對聚類探測的影響,首先利用具有不同 α 值的加權機制對網絡賦權, 然后利用一些著名的聚類算法運行并測試其準確性.這里使用在信息論中被廣泛研究的標準化互信息(normalized mutual information, NMI)來衡量聚類結果的準確性[40].NMI位于區間[0, 1]內, 其值的大小表明真實聚類和模型結果之間重疊的比例.特別地, 當NMI的值為1時, 算法結果與真實聚類完全相同, 具有最高的劃分效率.真實劃分X和模型結果Y之間的標準化互信息NMI的數學定義為

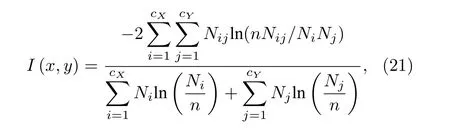
其中, cX和 cY分別表示真實劃分X和模型結果Y中的聚類數量.在(21)式, Nij代表真實劃分中聚類i和實驗結果中聚類j之間重疊的節點數量,Ni和 Nj分別表示矩陣N中第i行和第j列值的總和.

圖7 (a)和圖7(b)給出了利用兩種著名算法,即模擬退火法(SA)[48]和Duch-Arenas法(DA)[49],在運用加權機制的網絡上的實驗結果, 圖中數據點為50次實驗結果的平均值.其中, SA算法被證明是效果最好的聚類算法之一, 然而其計算復雜性也較高.與SA相比, DA不僅在模塊化優化方面具備一定可靠性, 而且計算過程也相對簡單.從圖7(a)和圖7(b)可以看到, 當 α 值從–2降低到–4,逆加權模式對應的NMI值越來越高, 要優于無權網絡.相反, 在原加權模式中, 當 α 值從2增加到4,加權網絡的NMI相對于無權網絡的NMI卻越來越少.這些結果均驗證了本文的加權策略的有效性.此外, 通過比較兩種方法發現, 圖7(a)中α=4( α =?4 )和 α =2 ( α =?2 )兩 種 情 況 的NMI差異區間小于圖7(b).這可能是因為, 即使是在無權網絡中, SA都擁有更高的精確度, 難以通過加權策略提高它的表現.但是對于DA來說, 通過提高α, 加權機制能夠大幅提高它的計算精度.

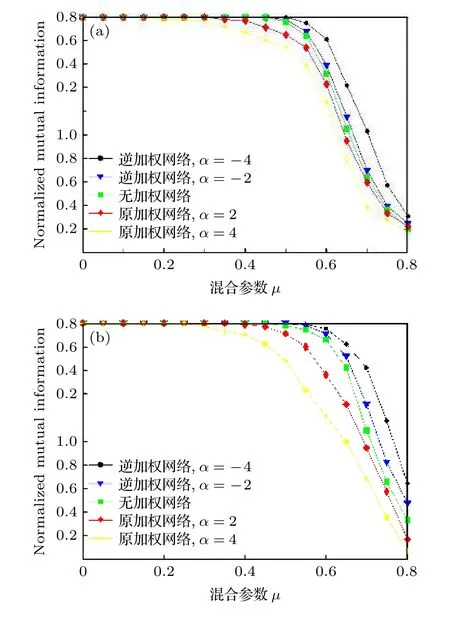
圖7 在LFR網絡中運用加權機制(逆加權機制), 當取不同的 α 值時, 利用(a) SA算法和(b) DA算法后NMI的計算值Fig.7.Weighted mechanism (inverse weighted mechanism)is used in LFR network.When the α value is different, the NMI value is calculated by using (a) SA algorithm and (b) DA algorithm.

此外, 本文還考慮了聚類規模的影響, 驗證結果如圖8所示, 圖中數據點為50次實驗結果的平均值.考慮兩種不同聚類規模條件下的LFR基準網絡, 其中, 每個聚類的節點數量在10—50之間為小聚類網絡, 在20—100之間為大聚類網絡.為了增強這兩種LFR基準網絡的可比性, 規定它們的區別僅限于聚類的規模大小, 其他方面的性質則完全相同.圖8驗證了在逆加權網絡中, SA和DA算法的準確性都得到提升.此外, 通過比較不同規模LFR網絡的聚類結果可以看出, 大聚類網絡中兩種算法的精確度更低, 這可能是因為小聚類網絡中具有更多的類間邊, 而類間邊更可能是被加權的.并且通過比較兩種方法, 圖8(a)顯示的小聚類和大聚類LFR網絡(無論是逆加權網絡還是加權網絡)之間的NMI區間差距小于圖8(b), 原因與圖7相同, 完美證明了本文加權機制的有效性.

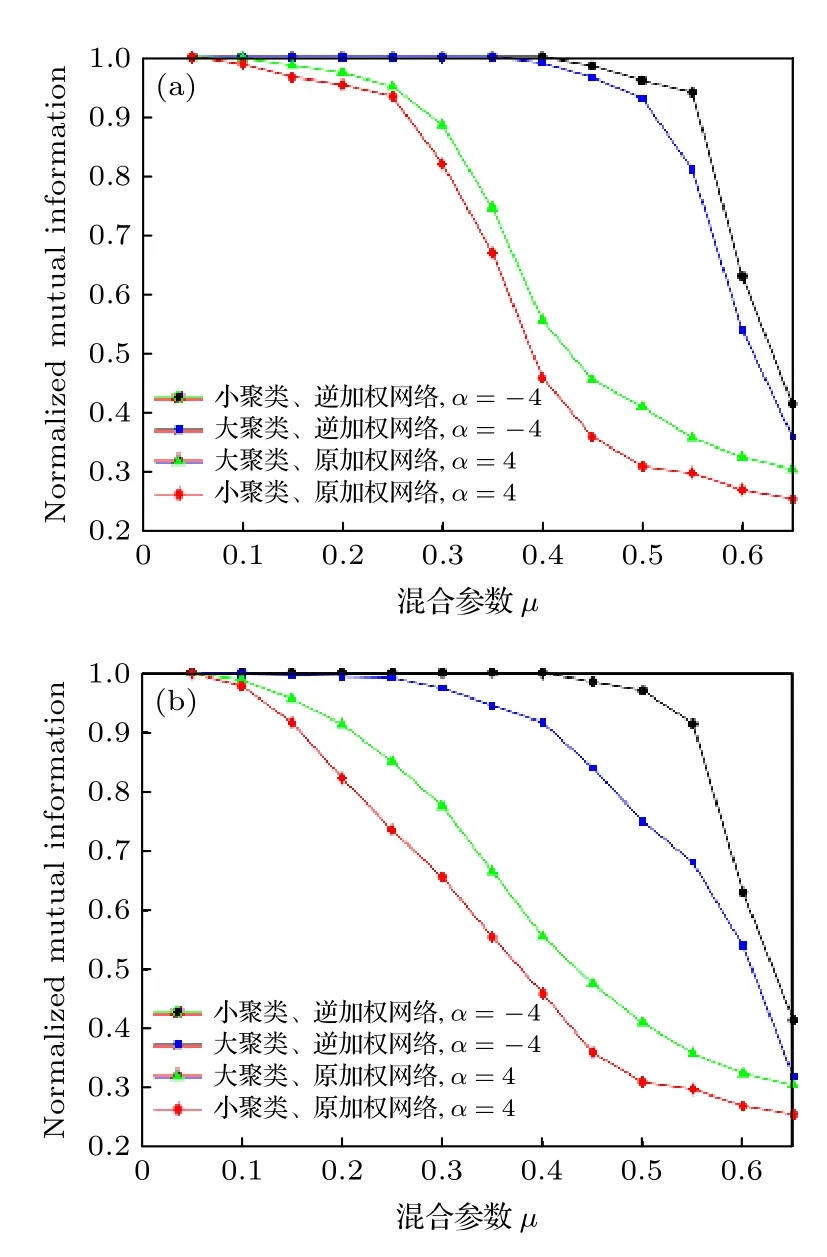
圖8 在LFR網絡中運用加權機制(逆加權機制), 當α=4( α =?4 )并考慮聚類規模時, 利用(a) SA算法和(b) DA算法后NMI的計算值Fig.8.The weighted mechanism (inverse weighted mechanism) is used in LFR network.When α = 4 (α = –4) and considering the cluster size, the NMI calculated by (a) SA algorithm and (b) DA algorithm.

2) 現實世界網絡

進一步將加權策略應用到現實世界網絡中, 結果在表2中列出.這里使用了7種廣泛使用的網絡, 并標識了相應的文獻出處.為了便于比較,提供了關于7種網絡已發表方法中的最優模塊度Q值[56].本文計算了當 α =4 時三種代表性算法,即SA[48], DA[49]和CNM[10]的加權前后模塊度Q值, 其中“/”左右表示加權后和加權前的模塊度Q值, 結果如表2所列.這三種算法的精確度雖然并不處于最頂級的行列, 然而正如表2所列, 在應用加權策略后, 結果非常接近已發表的最優值, 并且計算過程更加簡便.

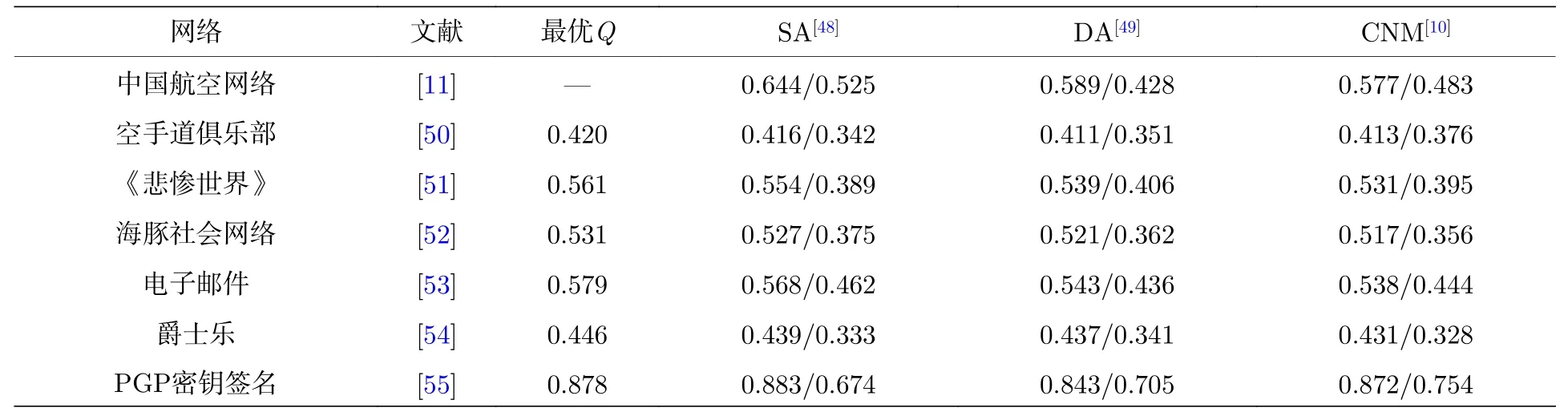
表2 在不同現實網絡使用加權策略得到的實驗結果, 其中“/”左右表示加權后和加權前的模塊度Q值Table 2.Experimental results are obtained by using weighting strategy in different real networks, where /’s left or right represents the modularity Q value after or before weighting.

進一步將9種加權策略應用到現實世界網絡中, 包括Chavez方法[21]、Wang方法[22]、Jalili方法[23]、Khadivi方法[31]、模擬退火(SA)算法[25]、隨機游走(RW)算法[27]、變分貝葉斯(VB)算法[29]、概率推斷方法[30]和本文方法, 用以對比不同加權方法的聚類效果.聚類算法統一使用CNM方法[10],并計算當 α =4 時的模塊度Q值.結果列在表3中, 可以看出, 本文所使用的加權機制的性能超過了其他所有的加權方法, 從而驗證了本文加權算法的高效性.

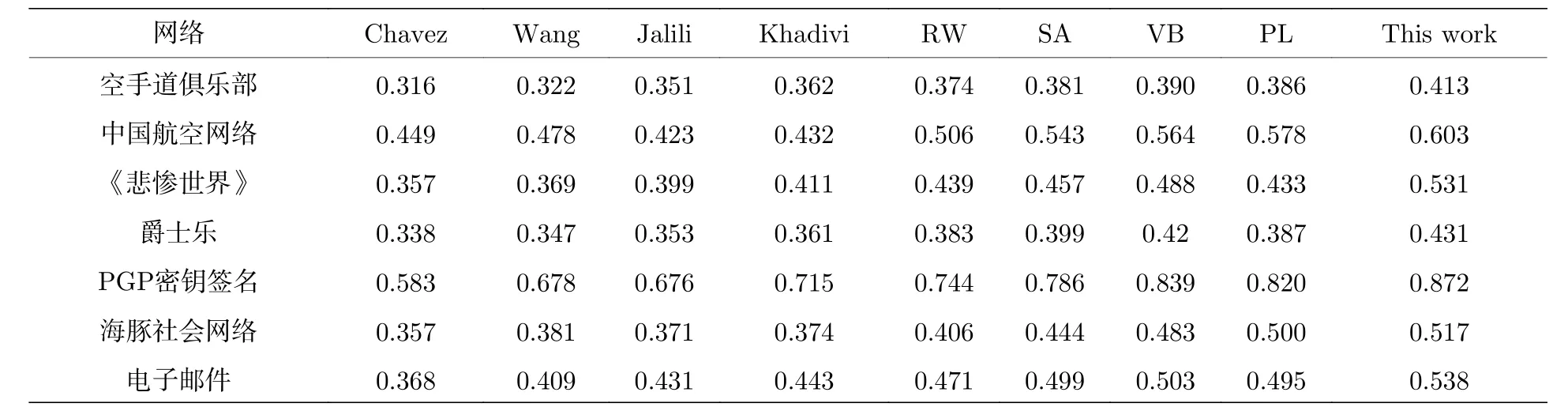
表3 在現實世界網絡中使用不同加權策略的實驗結果對比, 這里網絡聚類算法利用CNM算法, 其中RW代表隨機游走方法, SA代表模擬退火方法, VB代表變分貝葉斯方法, PL代表概率推斷方法Table 3.Comparison of experimental results using different weighting strategies in the real world network.CNM algorithm is used as the network clustering algorithm, in which RW represents the random walk method, SA represents the simulated annealing method, VB represents the variable dB method, and PL represents the probability inference method.

6 結 論

隨著“大數據”技術的不斷涌現和發展, 如何處理大規模網絡已經成為了巨大的現實挑戰[57,58].同時, 作為一個開放性問題, 提高網絡同步性能或聚類探測的算法效率往往非常困難.為此, 本文提出一個新型雙模式加權機制, 通過加權改變網絡拓撲結構來提高同步性能或聚類探測的算法效率.該加權機制包括兩種模式: 一是通過提高橋點的權重以增強同步能力的原始模式: 二是通過減少橋點的權重以提高聚類探測效率的逆模式.這種加權機制僅受一個參數 α 的影響, 因此非常便于實施.通過在人工基準網絡和現實世界網絡上的實驗分析, 檢驗了模型的有效性和高效性.特別地, 通過比較發現,本文提出的加權策略在效率上優于以往發表的提升網絡計算效率的加權方法.

在今后的研究工作中, 仍有一些問題值得深入探討.比如工程、信息領域應用中的群體演化博弈和平均一致性問題, 可能在無向網絡中更容易分析和理解, 加權有向網絡并不一定是最佳選擇.另外,如何在擁有數百萬甚至更多節點的超大規模網絡中進行研究分析, 也需要進一步深入探索.

感謝吉林大學劉大有教授、中國科學院數學與系統科學研究院章祥蓀研究員、中央財經大學劉志東教授對本文提出的建設性建議.