基于屬性數學理論的巖質邊坡穩定性評價

楊 濤

（四川省煤田地質局135隊，四川瀘州646000）

1 概述

巖質邊坡處于一個復雜而開放的系統當中，其工程地質性質受多種因素的影響和控制，具有很強的不確定性和模糊性，這決定了邊坡巖體的變形破壞特征是極為復雜的，因此，應用經典的數學模型來評價邊坡的穩定性存在著明顯的缺陷。傳統的巖質邊坡穩定性評價方法強調從結構面的角度出發建立巖質邊坡穩定性評價體系，利用定性和定量的評價方法，對邊坡穩定性做出綜合的評價，但對于實際情況中存在的模糊不確定性因素考慮不足，所得的評價結果往往不能反映出邊坡真實的穩定性狀況。為此，眾多學者將不確定性的評價方法引入到邊坡穩定性評價當中，包括灰色聚類分析[1]、層次分析法[2]、模糊綜合評價[3]、可拓學理論[4]等，各種方法的側重點不同，但都普遍存在著自身的局限性，如評價指標的選取和權重的賦值帶有很大的主觀性質，模糊綜合評判存在最大隸屬度失效的問題[5-6]等。屬性數學理論以屬性集、屬性測度空間和屬性識別為基礎，可以實現對定性描述的度量和有序分割類的識別。本文基于屬性數學理論，建立起巖質邊坡穩定性評價模型，構造屬性測度函數，以相似數[7]的方法確定各評價指標的權重，然后獲得綜合屬性測度，用置信度準則進行巖質邊坡穩定性的判別和評價。經過工程實例驗證表明：評價結果基本符合實際情況，這為科學的評價巖質邊坡的穩定性提供了一種新的思路和方法，對于類似的工程具有借鑒意義。

2 屬性數學評價理論

屬性數學理論是我國程乾生教授[5-6]提出的，它可以解決某類具有多個模糊屬性的綜合評價問題。屬性數學評價模型包括單指標屬性測度、多指標綜合屬性測度和屬性識別三部分。設x為評價對象空間，xi(i=1,2,…,n)為評價空間x的第i個評價對象，其有m個評價指標I j(j=1,2,…,m)和與之相對應的測量值t j，對于測量值t j，都有K個評價等級C k(k=1,2,…,K)。屬性評價空間F={評價等級}=(C1,C2,…,C K)，評價空間內每一種情況為一個屬性集,例如將巖質邊坡的穩定性評價等級分為C1={Ⅰ級}={穩定}、C2={Ⅱ級}={較穩定}、C3={Ⅲ級}={基本穩定}、C4={Ⅳ級}={不穩定}、C5={V級}={極不穩定}。評價對象的屬性級別用屬性測度來表示，因此可以用屬性測度值來定量化確定t ij的評價等級。由于屬性測度之間滿足相加性規則，從而可以對評價對象x i進行綜合屬性評價。

2.1 單指標屬性測度

設評價指標I j的測量值為t j，具有屬性級別C k，其屬性測度值μijk=μ（t ij∈C K），按照屬性測度的性質，μijk需滿足：

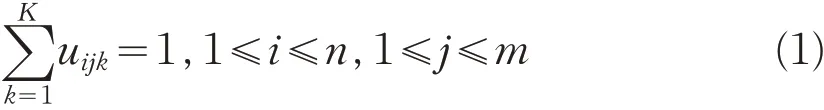
對指標I j建立對應的屬性測度函數，以表示屬性測度的變化情況。用表1中的形式來建立屬性測度函數。

表1 單指標等級劃分

表 1 中 ，a jk滿 足a j0＜a j0＜…a jk，或a j0＞a j0＞…a jk。令

當a j0＜a j0＜…a jK時，單指標屬性測度函數參考文獻[8]；當a j0＞a j0＞…a jK時[9]，根據公式（2）～（4）形式構造單指標屬性測度函數：

式（2）～（4）中 ，k=1,2,…,K-1 ，j=1,2,…,m。

2.2 多指標綜合屬性測度

對于評價對象x i各單指標的屬性測度μijk=μ（t ij∈C K），其綜合屬性測度由加權求和得到。μxk可按下式計算：

式中：ωj——第j個指標I j的權重，滿足0≤ωj≤1，

用相似權方法確定各評價指標的權重。首先假定評價對象x i各單指標的權重相同，即令ωj=1/m，由式（5）求出指標綜合屬性測度評價矩陣，若單指標屬性測度(u i j1,u ij1,…,u ijK)與綜合屬性測度(u i1,u i1,…,uiK)越近似，則表明I j越能反映總體情況，其權重越大。令r j為相似系數，ωj為相似權，由公式（7）和（8）求得，相似權ωj可作為評價指標I j的權重。最后將相似權值重新代入公式（5）求得綜合屬性測度。

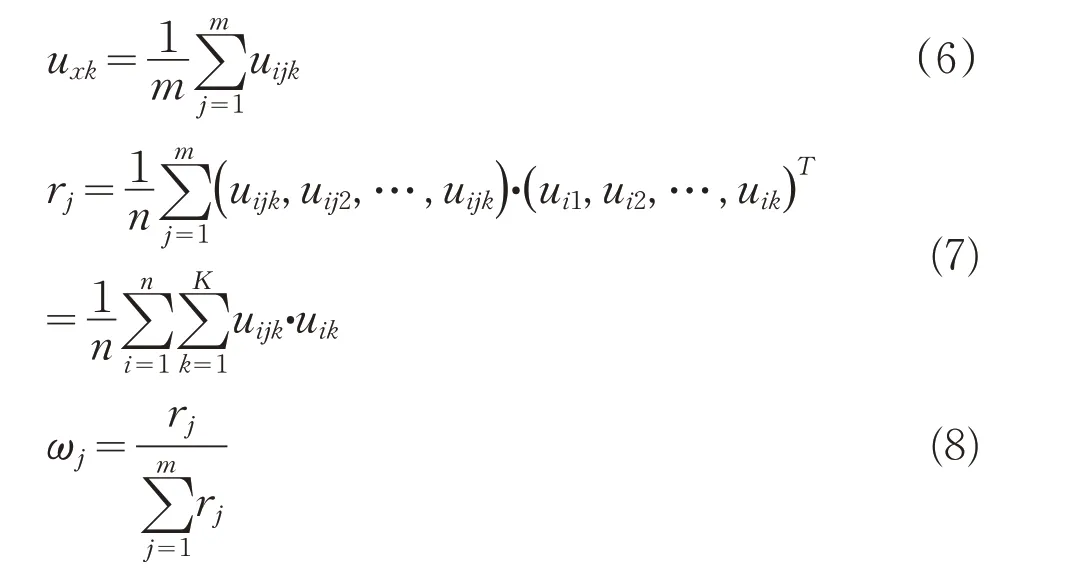
2.3 屬性識別

在屬性綜合評價中，如果(C1，C2，…，C K)為屬性空間F的分割，并且滿足C1＞C2＞…＞C K或C1＜C2＜…＜C K，則稱(C1，C2，…，C K)為有序分割，一般采用置信度準則判定評價對象x i屬于哪一個評價等級C K。置信度準則：設λ為置信度，且0.5＜λ≤1，一般取0.6～0.7之間。

當C1＞C2＞…＞C K時，若滿足：

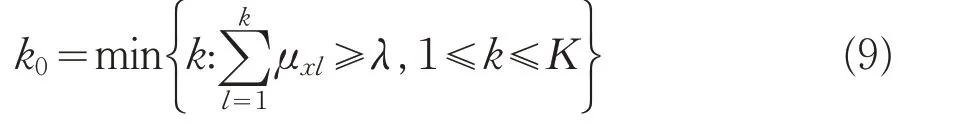
則認為x屬于C K0級別。

當C1＜C2＜…＜C K時，若滿足：

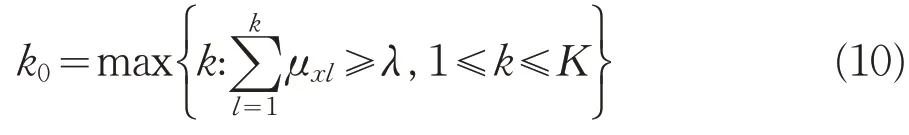
則認為x屬于C K0級別。

3 巖質邊坡危險性評價指標體系

3.1 評價指標的選取[4]

巖質邊坡的穩定性受巖體的結構特征、巖性、地形地貌和應力環境等多種因素的綜合影響，某些因素對邊坡的穩定性起控制性作用，某些因素則是邊坡失穩破壞的觸發因素。文中巖質邊坡的穩定性評價選取7個評價指標：I1={RQD}；I2={巖體結構特征}；I3={地應力}；I4={內聚力}；I5={內摩擦角}；I6={坡高}；I7={日最大降雨量}；將巖質邊坡穩定性等級分為穩定、較穩定、基本穩定、不穩定和極不穩定5個等級，各指標評價等級劃分見表2。

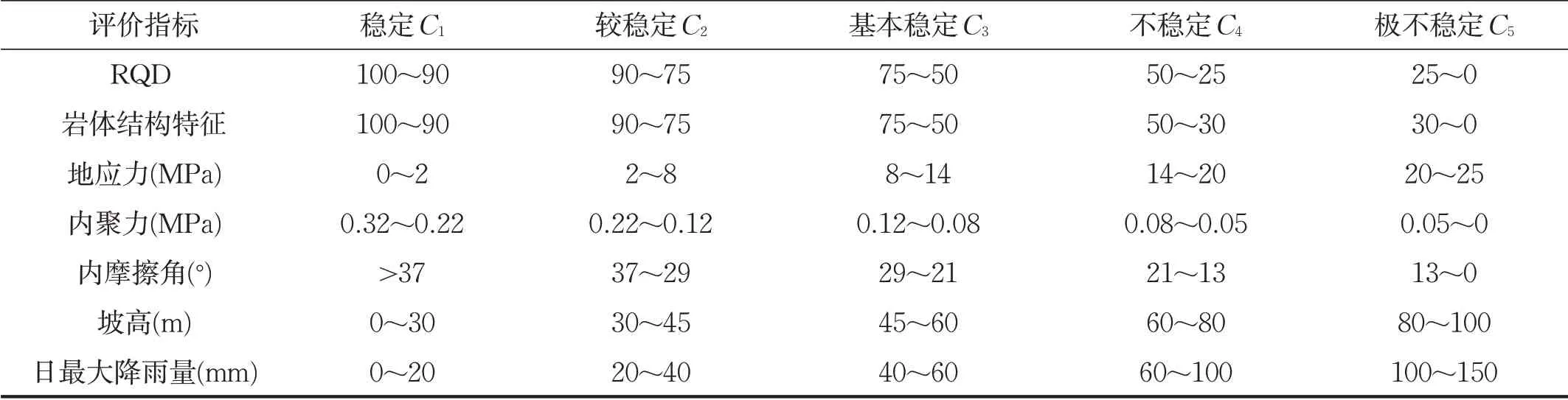
表2 巖質邊坡穩定性評價指標和分級標準

3.2 評價指標的屬性測度分析

以首鋼某區域的邊坡[4]為例，進行巖質邊坡穩定性屬性識別分析。該區域出露地層以變質巖為主，地質構造復雜，選取三類巖質邊坡作為待評價邊坡，進行邊坡穩定性屬性識別分析，見表3。根據公式（2）～（4），結合表2中的分類標準來構造單指標屬性測度函數，限于篇幅，文中僅列出評價指標I1的屬性測度函數，如下所示。

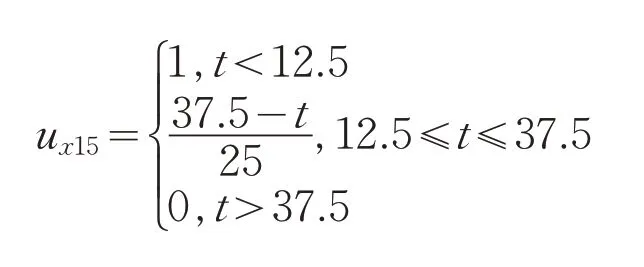
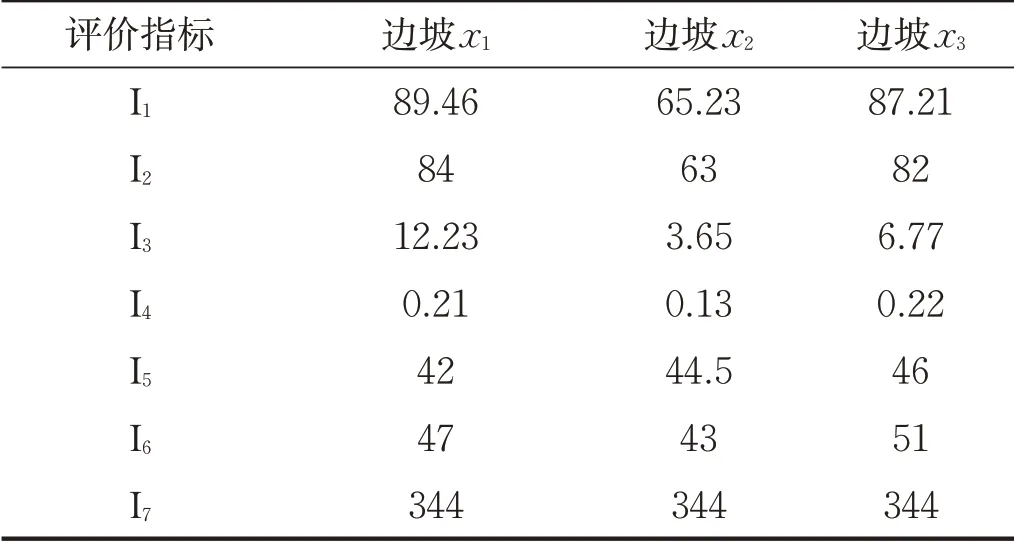
表3 待評價邊坡評價指標值

根據表3中的數據和構建的屬性測度函數，可求得各評價對象的單指標屬性測度評價矩陣。以評價對象x1為例，將測量值代入屬性測度函數中，計算可得x1的單指標屬性測度評價矩陣。首先假設各項指標的權重相等，得到各單指標的權重為1/7，依據公式（6）～（8）計算可得到相似數：(0.362，0.387，0.328，0.337，0.218，0.276，0.143)，然后得到5個指標的相似權：（0.176，0.189，0.16，0.164，0.106，0.135，0.07），即為各項指標的權重，最后計算得到評價邊坡x1多指標綜合屬性測度，見表4。

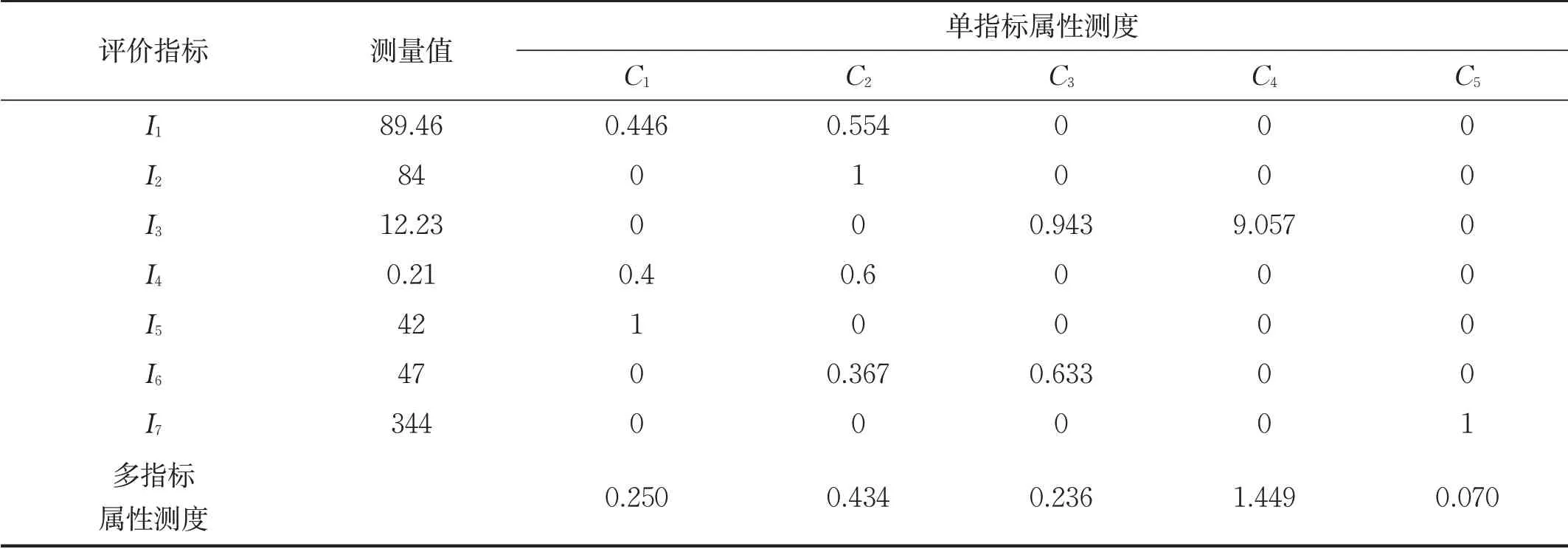
表4 邊坡x1屬性測度分析

3.3 屬性測度分析

屬性識別分析就是由多指標綜合屬性測度u xk判斷評價對象屬于哪一個評價級別，取λ=0.65，根據公式（9）進行屬性識別，可以判定邊坡x1的危險性等級為C3，即較穩定。依次可得到各評價樣本的屬性識別結果，基本符合實際情況，見表5。將評判結果與文獻[4]中的評價結果對比，可以看出屬性識別結果與物元可拓評判結果有較好的一致性，這表明利用屬性識別分析來評價巖質邊坡的穩定性是合理和可信的。

表5 屬性識別結果

4 結論

（1）基于屬性數學理論，建立巖質邊坡穩定性評價模型，為巖質邊坡穩定性評價提供了一種新的思路和方法。選取7種因素作為邊坡穩定性評價的指標，構建屬性測度函數，獲得指標的屬性測度值，利用置信度準則進行屬性識別分析。該方法理論基礎嚴謹，數學意義明確，具有較強的實用性。同時該評價模型采用相似數方法獲取指標權重，避免了傳統權值確定的主觀性和隨意性，從而保證了評價結果的客觀性和準確性。

（2）通過工程實例驗證，并與物元可拓評判結果對比，結果表明二者評判結果基本一致，表明該模型的評價結果是準確可信的。巖質邊坡的穩定性受多種因素的影響，其發展演化過程具有高度的不確定性，因此，其評價指標的選取和分級以及權重的確定等方面還需要進一步的研究。