一種基于網絡模型的任務可靠性預計方法
陸志毅 周云 王璟玢
(1.中國人民解放軍海軍裝備部駐上海地區軍事代表局 上海市 200241 2.中國航空無線電電子研究所 上海市 200241)
網絡可靠性概念最先針對通信網絡提出,其評估模型基于圖論和設備物理失效,研究主要集中于改進算法和降低計算復雜度。20世紀90年代開始網絡可靠性研究成為熱點,提出了包括連通可靠性在內的很多網絡可靠性概念,以及基于二元決策圖(Binary Decision Diagram,BDD)等算法的方法論。21世紀后,對無線移動網絡可靠性的研究成為熱點,同時針對復雜網絡的一些研究方法和成果也給復雜系統可靠性研究帶來新的啟發。
BDD作為一種描述布爾函數的數據結構,最早由AKERS提出,用來操作大數據函數[1]。之后,BRYANT給出了BDD的基本操作及算法[2],BDD得以廣泛應用于硬件電路驗證、組合優化、規劃調度等研究領域中。
可靠性分析方面,COUDERT最早研究將BDD方法用于可靠性分析[3],并且BDD在網絡連通可靠性分析領域的應用研究獲得了大量的成果,實驗證明利用BDD能夠有效提升網絡可靠性分析的性能。在一般的可靠性分析中,RAUZY等在內的大部分設計研究人員,主要將BDD用作故障樹定量分析的工具[4],這雖然體現了BDD技術高效、精確的優勢,但是就整個可靠性分析過程而言,仍較為繁瑣。
任務可靠性是航電系統的重要指標,主要的分析方法有GO法,Petri網,以及包括可靠性框圖、故障樹和Markov分析等在內的典型可靠性建模分析方法。GO法依靠操作符和信號流建立GO圖,然后按照信號流向和操作符運算規則進行計算。Petri網方法在系統功能性能設計基礎上進行系統狀態分析,進一步建立表征系統狀態轉變的Petri網模型,依靠對每次狀態轉換的定量分析,最終實現全過程的可靠性分析。以上方法建模分析過程較為復雜,部分存在狀態爆炸的問題。
本文在BDD的網絡連通可靠性分析方法,和傳統的任務可靠性分析方法基礎上,提出了一種基于網絡模型的任務可靠性分析方法。將產品的可靠性特征抽象為網絡模型,并利用基于BDD的網絡連通可靠性分析方法,來對其進行分析,省略了前級的故障樹分析過程,具有建模過程簡單、分析高效準確、便于計算機自動化分析等優點。
1 BDD算法
1.1 基本概念
BDD是基于香農分解的有向無環圖,是BDP(Binary Decision Program)的圖形化表示,是對香農分解的簡約化表達,可直觀反映函數的邏輯結構。其數據結構空間高效合理,操作方法省時有效。
香農分解定理:令f是基于變量集X(X∈Bn)的布爾表達式,且x為變量集X中的任一變量,則:
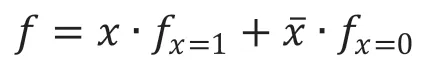
其中在fx=1表示x=1時f的值。
香農分解是BDD分析和求解的基礎。為簡化表達香農分解,引入ite算子,香農分解定義為:
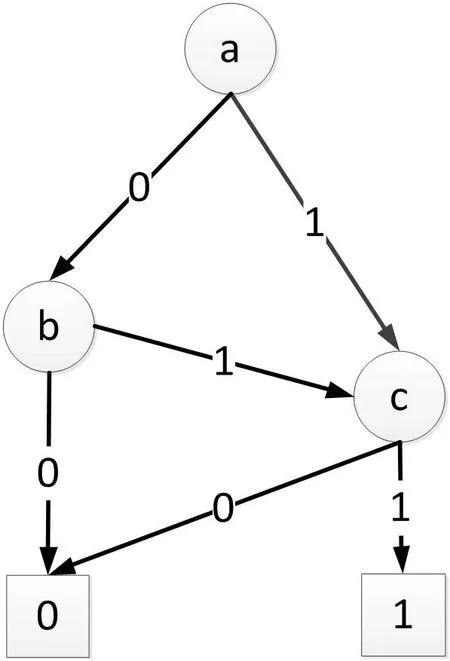
圖1:BDD示例
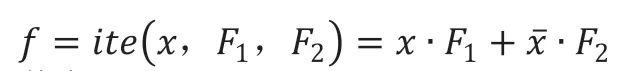
其中F1=fx=1,F2=fx=0
BDD表示為G=
在BDD的基礎上,對變量順序施加約束后生成有序二元決策圖(Ordered BDD,OBDD)。對OBDD進行約簡,使其不包含同構子圖,且節點的兩條邊指向不同節點,得到約簡的OBDD(Reduced and Ordered BDD,ROBDD)。ROBDD對布爾函數的表達更為簡潔有效,沿根節點向下索引時,每個節點在每條邊上出現不多于1次,且為升序。
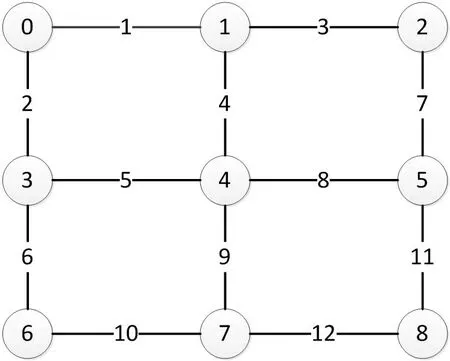
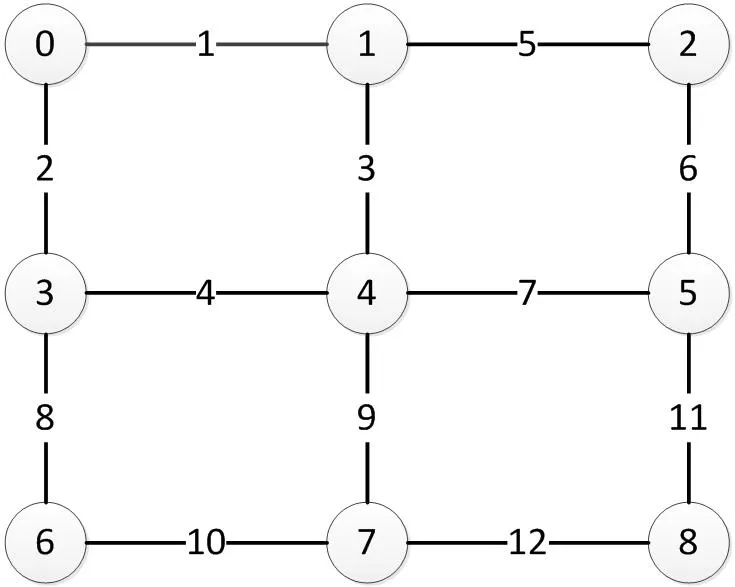
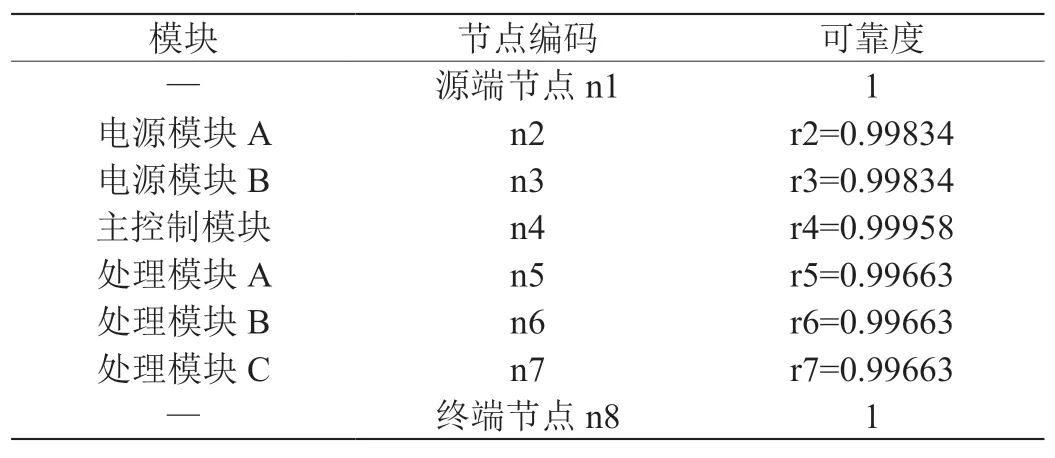
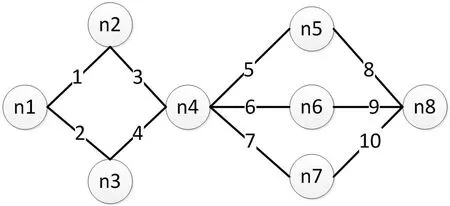
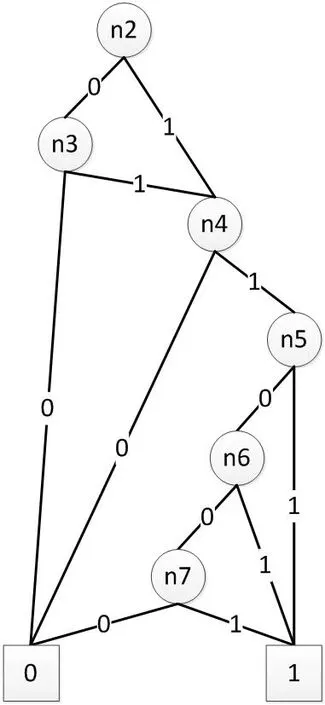
對ROBDD的構造而言,首先需要對變量順序施加約束,為所有變量分別創建索引,并且保持變量索引順序在整個構造過程中不發生改變。例如xi BDD規模和計算量依賴于變量排序,不合適的排序會使BDD規模變得很龐大。目前針對BDD排序有很多算法,如精確變量排序算法,動態變量排序算法,啟發式變量排序算法,優先排序變量和道路排序分解策略等等。其中,廣度優先排序策略(BFS)和優先級排序策略(POS)應用比較廣泛。 1.2.1 廣度優先排序策略(BFS) 廣度優先邊排序策略,是基于廣度優先原則索引所有網絡節點,并在索引過程中對未排序的邊實施排序。 圖2:BFS排序示例 圖3:POS排序示例 圖4:某綜合處理設備功能原理圖 對給定網絡G=(V,E),廣度優先排序的過程如下: (1)取?u∈V作為廣度優先排序的起點,標記u 狀態為已檢索,并將u 放入FIFO; (2)若FIFO中存在元素,取元素u,檢索與u 關聯的邊ei=(u,vi)并進行排序,如果vi未標記為已訪問則完成標記后放入FIFO; (3)重復步驟ii至FIFO為空,即完成排序。 以3×3晶格網絡為例,對各邊進行廣度優先排序,圖2為排序結果。 1.2.2 優先級排序策略(POS) 優先級排序策略的主要過程為:先按節點優先級規則完成節點排序,若關聯多條邊的兩個節點都已排序,則以邊優先級規則對這些邊排序。優先級排序策略的節點優先級規則如下: (1)關聯的節點中已排序節點數量多的優先; (2)關聯的節點中已排序節點數量相同時,其關聯已排序節點排序靠前的節點優先。 優先級排序策略的邊優先級規則如下:與邊關聯的已排序節點排序靠前的邊優先。以3×3晶格網絡為例,對各邊進行優先級排序,圖2為排序結果。 表1:模型信息 1.3 基本運算 為了計算的方便,BDD的運算一般不直接進行香農分解,主要直接采用一些基本運算規則。 令布爾表達式P和H如下: ◇表示任意邏輯運算,則P和Q之間的邏輯運算用 BDD 運算表示如下,: 連通可靠性是最早開始的網絡可靠性研究,與傳統可靠性一致,以概率統計理論為基礎,輔以圖論作為網絡“拓撲特殊”的支持,是目前網絡可靠性中最被認可的部分。 本文探討的任務可靠性網絡模型,主要思想是將與系統任務完成相關的功能流和數據流關系,以有源網絡形式進行表達,將任務可靠性分析問題轉化為有源網絡源端到終端的兩端連通可靠性問題。任務可靠性網絡模型可表達為: 其中N表示模型的節點集合,L表示模型的邊集合,R表示節點可靠度集合。 設N中有m個節點,則任意節點ni(ni∈N,1 從節點np到節點nq的任意邊lj=(np,nq),lj∈L,表示為保證任務的完成,節點np到節點nq間的功能或數據流。 任意元素ri∈R,表示節點ni的可靠度,規定幾點S和T的可靠度值為1。 在本文的模型中有以下假設: (1)任一節點ni只存在正常(即ni=1)和故障(即ni=0)兩種狀態; (2)任兩個節點間的故障是相互獨立的; (3)任一邊lj為正常狀態; (4)布置表征任務開始的網絡源節點S; (5)布置表征任務成功的網絡端節點T; (6)對任務可靠性分析層次相應設備進行編號,將已編號設備布置為中間節點; (7)根據任務活動,添加網絡的邊,使源端節點S連接到終端節點T。 圖5:任務可靠性網絡模型 圖6:任務可靠性網絡模型BDD 基于網絡模型預計任務可靠性,即為計算網絡模型源端節點S到終端節點T的連通可靠性。基于ROBDD的網絡模型任務可靠性分析,基本思想為:先由網絡的最小路集求得網絡的BDD,然后根據BDD求解連通可靠性的不交化積和表達式,最終完成任務可靠性預計。 假設有向網絡的節點集為N={ni}(i=1,2,…,s),邊集為L={li}(i= 1,2,…,t),若要求n1到nt的可靠度,算法過程如下: (1)從源節點開始,利用BFS或POS等排序策略對任務可靠性網絡模型各邊進行排序; (2)求出n1到nt的最小路集。設已求出為為網絡模型最小路集的邏輯結構函數.其中,m表示最小路集數,fj表示某條最小路集j的所有節點布爾值的與; (3)按照排序結果,作f的BDD; (4)在邏輯結構函數f的BDD上搜索從根節點到葉結點為1的路徑,則可獲得F的不交化最小路集其中gi表示最小路集經變換后得到的不交和,p表示變換后得到的不交和項的項數。 任務可靠度可用下面的概率和公式直接進行計算: 考慮某綜合處理設備,其功能原理如圖4所示。 該綜合處理設備主要完成數據處理任務,具有雙余度電源設計,由主控制模塊進行資源調度,由三個處理模塊提供數據處理的硬件資源,主控制模塊視當前資源占用情況,調用其中一個完成當前數據處理需求。 任務可靠性分析在模塊層面進行,對各模塊進行編碼,并求得時刻t的可靠度,如表1所示。并建立任務可靠性網絡模型,利用POS排序策略對模型中各邊進行排序,如圖5所示。 列出圖5所示網絡,其邏輯結構函數為: 進一步作出該表達式對應的BDD見圖6。 由BDD列出ST連通可靠性的不交化和表達式,即綜合處理設備的任務可靠性表達式: 計算得任務可靠度R=0.9995772,與使用可靠性框圖模型求解的結果一致。 BDD方法被廣泛用于網絡連通可靠性求解,對復雜的邏輯關系計算呈現出較高的效率和準確度。本文在網絡連通可靠性基礎上,提出了一種根據產品功能流和數據流建立的網絡模型,并將產品任務可靠性轉化為網絡連通可靠性進行求解的方法,給出了模型建立和基于BDD進行求解的方法。最后本文介紹了一個示例,說明該方法是可靠的。任務可靠性網絡模型BDD如圖6。 該方法尚需進行更多的模型轉化、模型規范等方面的研究,但是提供了面對復雜系統的任務可靠性預計的一種新思路,有以下兩方面可能的優勢: (1)模型建立方式簡單,便于利用各種語言和建模方式描述的功能性能模型直接轉化而來,便于與基于模型的系統工程結合。 (2)計算方式高效,準確,利于計算機進行計算,方便形成計算機輔助分析的工具鏈。1.2 排序策略
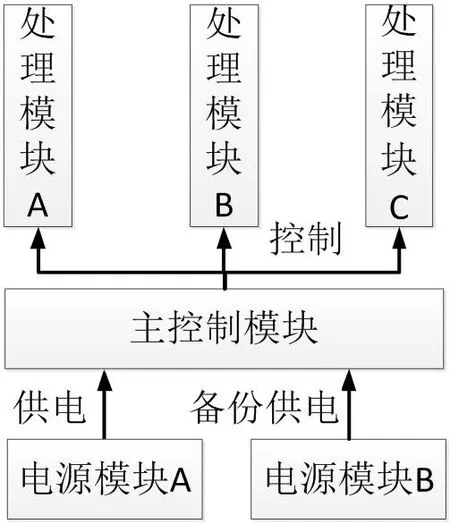
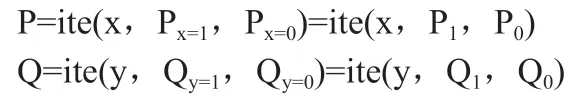
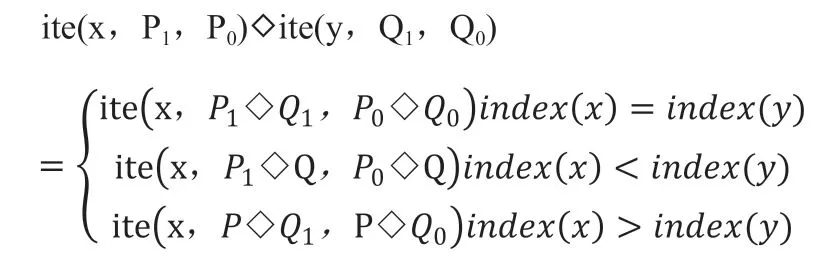
2 任務可靠性預計
2.1 網絡結構模型
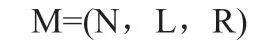
2.2 任務可靠性預計
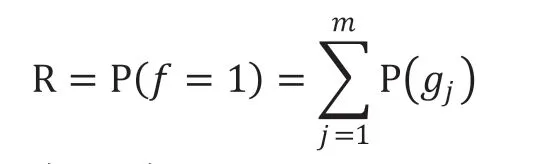
2.3 案例分析


3 總結

