二維函數光子晶體中的類Dirac點及帶隙結構

任明麗, 楊涪銓, 劉 晗, 韓 夢, 朱翔久, 姜明奇, 吳向堯

(吉林師范大學 物理學院, 吉林 四平 136000)

近年來, 光子晶體材料在許多領域應用廣泛. 如石墨烯被用作潤滑劑, 由于其片狀結構, 因此大量碳原子在同一平面內緊密結合, 在范德華力的作用下上下薄片間僅微弱附著, 這種弱的層間相互作用使提取原子或幾層原子成為可能[1-2]; 二硫化鉬(MoS2)已用于設計二維光源、 晶體管、 偏振選擇器和光電探測器等光電器件[3-6]. 二維MoS2與塊狀材料相比, 其單層膜結構的直接帶隙使光致發光得到加強[7], 得到了更小的有效激子Bohr半徑(1 nm)和較大的激子結合能(0.96 eV), 為實現在室溫下的激子器件研發提供了條件[8], 其偶極取向的二維特性使激子發射具有高度的各向異性[9].

與三維光子晶體材料相比, 二維光子晶體材料具有許多獨特性能. 首先, 垂直于二維平面方向的量子局域產生了新的電學和光學性質, 這些性質與三維情形明顯不同[10]. 其次, 二維材料的表面會自然鈍化任何懸垂鍵, 從而使二維材料易與波導和空腔等光子結構集成. 由于異質結構中晶格常數不同的層與層狀體材料的范德華力結合較弱, 因此使用不同的二維材料可構建垂直異質結構而不存在傳統的晶格失配問題[11]. 最后, 由于二維材料的原子層較薄, 因此它們與光的相互作用更強[12].

在研究石墨烯的電子能帶結構中提出了Dirac點[13-15], Dirac點通常出現在第一個Brillouin區內, 在帶隙結構中, 上、 下導帶間以線性方式相交, 產生一個Dirac錐, 在該點上, Maxwell方程組可被不含質量的Dirac方程取代[16]. 在光子晶體結構中可模擬石墨烯中的Klein隧道效應和Zitterbewegung效應[17-19]. 此外, Dirac點可研究光子晶體中的局域態模式, 稱為Dirac模式[20]. 目前, 已對三角形、 蜂窩形、 阿基米德式和類蜂窩形晶格的光子晶體中Dirac模式進行了研究[21].

在正方形晶格的光子晶體Brillouin區中心存在線性色散關系. 半Dirac點是一類研究特殊電子帶隙色散關系的新模式[22], 由能帶在Brillouin區中心或邊界上相交于一點形成. 在二維(2D)Brillouin區費米面的一個點附近, 色散關系沿對稱軸是線性關系, 在垂直方向為二次形式, 研究表明, 該半Dirac點與半金屬相和帶絕緣體間的拓撲相變有關[23].

由A和B兩種介質組成的一維函數光子晶體, 其折射率是關于空間坐標的函數[24-26], 與由介質折射率為常量的A和B兩種介質構成常規光子晶體不同. 本文研究二維函數光子晶體橫電(TE)和橫磁(TM)波模式的帶隙結構, 并在二維函數光子晶體中得到絕對帶隙和類Dirac點. 當介質柱半徑和介電常數的函數形式不同時, 帶隙結構發生相應改變. 因此， 利用二維函數光子晶體可設計所需的帶隙結構, 從而為光學器件的設計提供一種新方法.

1 二維函數光子晶體介電常數的Fourier變換

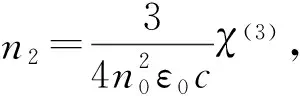
圓柱形介質柱的介電常數為

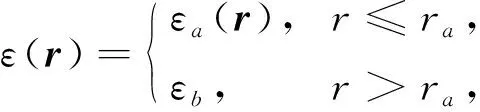
(1)

或表示為

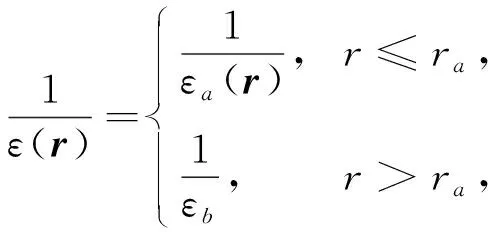
(2)

方程(2)可寫為

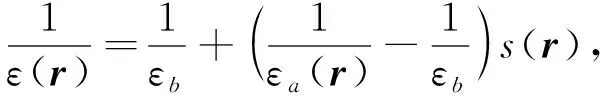
(3)

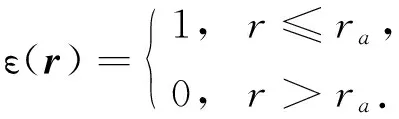
(4)

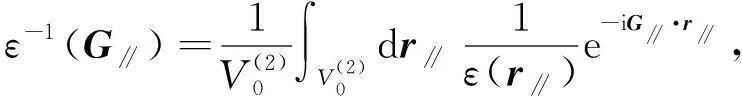
(5)

將方程(3)代入式(5)可得

其中

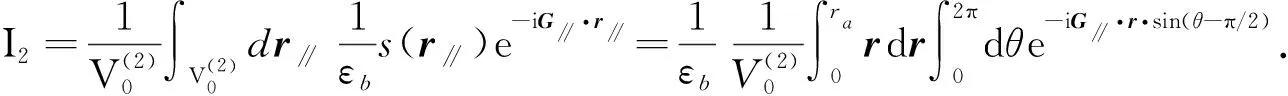
(8)

當|r∥|=r∥=r, |G∥|=G∥, dr∥=ds=rdrdθ時,r∥和G∥的夾角為θ.

由式(8)可得

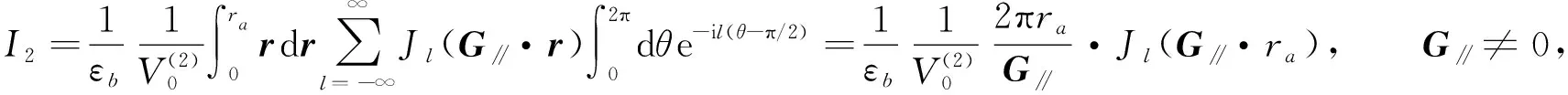
(9)

當G∥→0(m→0,n→0)時,

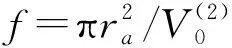
當G∥=0,J0(0)=1時, 由式(11)可得

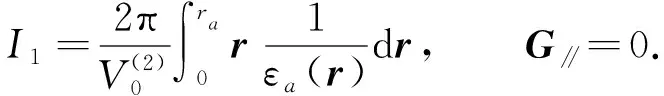
(12)

將I1,I2和I3代入方程(6)可得

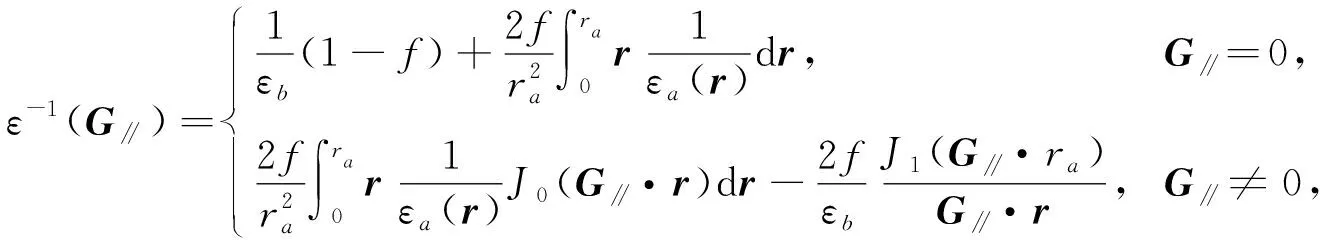
(13)

方程(13)稱為二維函數光子晶體介電常數的Fourier變換.當εa(r)=εa時, 若εa為常數, 則方程(13)變為

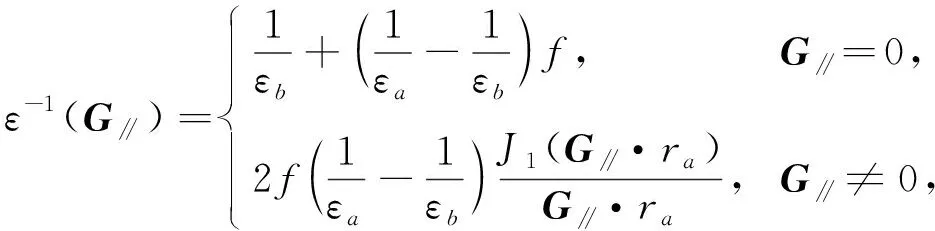
(14)

方程(14)稱為二維常規光子晶體介電常數的Fourier變換. 因此, 二維常規光子晶體是二維函數光子晶體的特殊情況.

用平面波展開法可得TM波和TE波的特征值方程[29-30]分別為

將式(13)代入式(15)和式(16), 可得二維函數光子晶體的帶隙結構.

2 數值分析

下面分析二維函數型光子晶體帶隙結構的數值結果. 分別用方程(13),(15),(16)計算二維函數光子晶體的帶隙結構. 設該光子晶體為三角形晶格, 圓柱形介質柱位于空氣背景板中. 研究介電常數是空間坐標的函數形式εa(r)=kr2+b(0≤r≤ra), 其中r為介質柱半徑,k為函數系數, 當k=0時, 它是常規型光子晶體, 當k≠0時, 變為函數型光子晶體, 令k=3×1012,b為常數項.研究常數項b對函數光子晶體帶隙結構的影響.

介質柱介電常數函數形式為εa(r)=kr2+b和b=8時三角晶格二維函數光子晶體TE模式和TM模式的帶隙結構如圖1所示, 其中k=3×1012, 介質柱半徑r=0.4a.由圖1可見, 當ωa/(2πc)=0～1時, TE波有5個帶隙, TM波沒有帶隙. 由于在帶隙結構譜中, 兩層能帶相交, 在一個方向上是線性的, 在另一個方向上是二次型的, 將這種交點定義為類Dirac點. 因此, 在TE波帶隙中有A和B兩個點為類Dirac點.

圖1 介質柱介電常數函數形式為εa(r)=kr2+b和b=8時三角晶格二維函數光子晶體的帶隙結構Fig.1 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=8

介質柱介電常數函數形式為εa(r)=kr2+b和b=9時三角晶格二維函數光子晶體TE模式和TM模式的帶隙結構如圖2所示, 其中k=3×1012, 介質柱半徑r=0.4a.由圖2可見, 當ωa/(2πc)=0～1時, TE波有5個帶隙, TM波有1個帶隙. 在TE波帶隙中有A和B兩個點為類Dirac點.

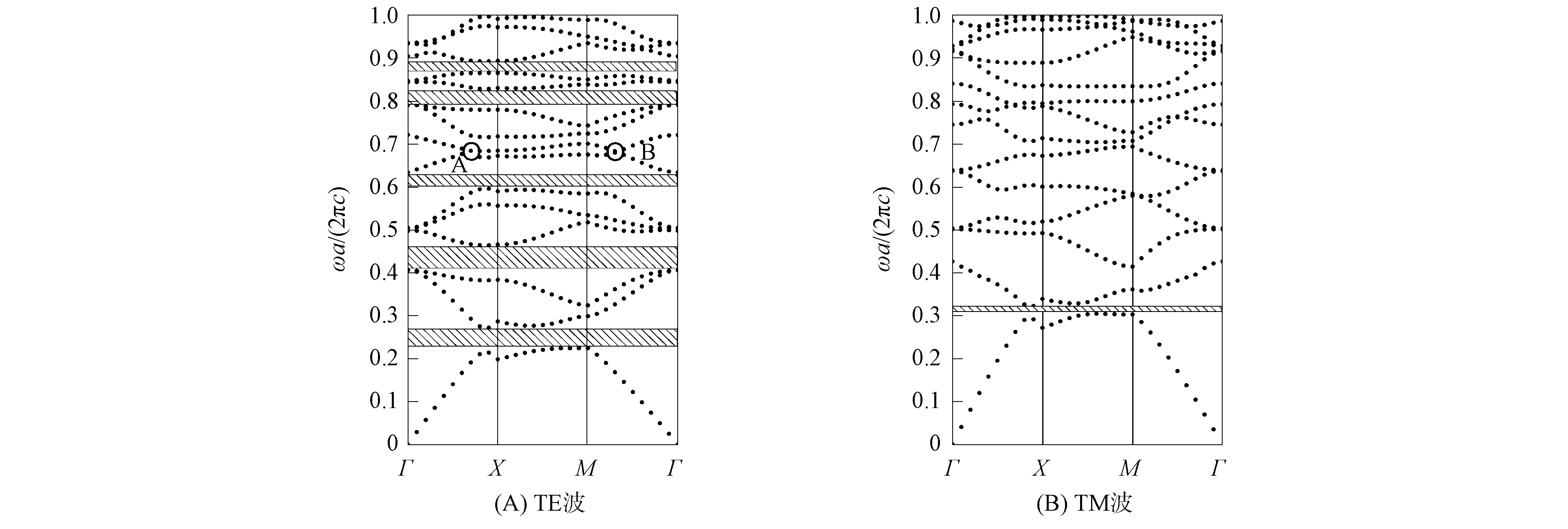
圖2 介質柱介電常數函數形式為εa(r)=kr2+b和b=9時三角晶格二維函數光子晶體的帶隙結構Fig.2 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=9

介質柱介電常數函數形式為εa(r)=kr2+b和b=10時三角晶格二維函數光子晶體TE模式和TM模式的帶隙結構如圖3所示, 其中k=3×1012, 介質柱半徑r=0.4a.由圖3可見, 當ωa/(2πc)=0～1時, TE波有5個帶隙, TM波有2個帶隙. 在頻率為0.4附近, TE和TM波的帶隙重合, 稱為完全禁帶. 在TE波帶隙中有A和B兩個點為類Dirac點.

圖3 介質柱介電常數函數形式為εa(r)=kr2+b和b=10時三角晶格二維函數光子晶體的帶隙結構Fig.3 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=10

由圖1～圖3可見, 隨著折射率函數常數項b的增加, 在TE波中的帶隙發生了藍移, 均出現2個類Dirac點, 并在TM波的帶隙中出現了新的禁帶, 表明改變常數項b可實現函數光子晶體能隙結構的改變.

介質柱介電常數函數形式為εa(r)=kr2+b和b=9,k=5×1012時三角晶格二維函數光子晶體TE模式和TM模式的帶隙結構如圖4所示, 其中介質柱半徑r=0.4a.由圖4可見, 當增加函數系數k時, 在TM模式的帶隙中出現了1個類Dirac點C, 兩種模式的帶隙均向低頻率偏移.

圖4 介質柱介電常數函數形式為εa(r)=kr2+b和b=9, k=5×1012時三角晶格二維函數光子晶體的帶隙結構Fig.4 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants εa(r)=kr2+b and b=9, k=5×1012

介質柱介電常數函數形式為ε(r)=k/(r+d)+b和r=0.2a時三角晶格二維函數光子晶體的帶隙結構如圖5所示, 其中k=7×10-6,d=2×10-6,b=11.由圖5可見, 當ωa/(2πc)=0～1時, TE波有3個帶隙, TM波有2個帶隙, 當ωa/(2πc)=0.46～0.57時, TE和TM波的帶隙中出現完全禁帶.

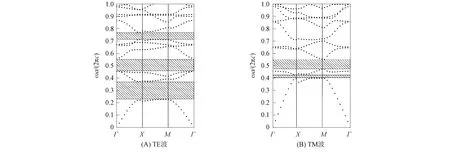
圖5 介質柱介電常數函數形式為ε(r)=k/(r+d)+b和r=0.2a時三角晶格二維函數光子晶體的帶隙結構Fig.5 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants ε(r)=k/(r+d)+b and r=0.2a

介質柱介電常數函數形式為ε(r)=k/(r+d)+b和r=0.3a時三角晶格二維函數光子晶體的帶隙結構如圖6所示, 其中k=7×10-6,d=2×10-6,b=11.由圖6可見, 隨著介質柱半徑r的增加, 在TE波帶隙中出現一個帶隙, TE波的帶隙結構逐漸藍移, 且完全禁帶的寬度逐漸變窄.

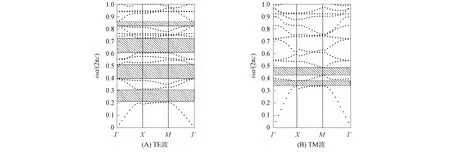
圖6 介質柱介電常數函數形式為ε(r)=k/(r+d)+b和r=0.3a時三角晶格二維函數光子晶體的帶隙結構Fig.6 Band gap structures of two-dimensional functional photonic crystals with triangular lattice when functional form of dielectric column dielectric constants ε(r)=k/(r+d)+b and r=0.3a

綜上, 本文設計了一種二維函數型光子晶體, 并計算了TE和TM波的帶隙結構. 結果表明： 在二維函數光子晶體中得到了絕對帶隙和類Dirac點； 當介質柱半徑和介電常數函數形式不同時, 帶隙結構發生改變, 利用二維函數光子晶體可設計所需的帶隙結構. 由于二維常規光子晶體的結構固定, 因此其帶隙結構不變. 若需一種新的帶隙結構, 則需對二維常規光子晶體進行改造. 對于二維函數光子晶體, 通過調節外部光強分布即可改變介質柱介電常數的函數形式, 同時調節介質柱的半徑, 可改變函數光子晶體的帶隙結構以及類Dirac點的位置.