基于CFD法預(yù)報(bào)組合螺旋槳的水動(dòng)力特性

王聲森 劉益平 張丁標(biāo) 蘭艷肖 張迪

摘要：螺旋槳是船舶的主要推進(jìn)裝置，船舶的推進(jìn)效率、燃料的消耗和排放量是設(shè)計(jì)的重要指標(biāo)。隨著計(jì)算機(jī)性能的提高，有限元法作為計(jì)算和評(píng)估螺旋槳水動(dòng)力性能的有效方法，能有效的模擬螺旋槳的運(yùn)行狀況，并獲得模擬數(shù)據(jù)。本文基于CFD數(shù)值模擬法對(duì)螺旋槳進(jìn)行有限元計(jì)算，比較在不同進(jìn)度系數(shù)下，不同湍流模型對(duì)螺旋槳水動(dòng)力性能的影響;研究螺旋槳的槳葉壓力及流場(chǎng)的變化趨勢(shì);揭示單槳、對(duì)轉(zhuǎn)槳和串列槳的運(yùn)行特性及敞水性能，為后續(xù)研究提供理論基礎(chǔ)。

關(guān)鍵詞：數(shù)值模擬;組合螺旋槳;CFD

中圖分類號(hào)：U664.33

文獻(xiàn)標(biāo)識(shí)碼：A

1 前言

隨著船舶行業(yè)的快速發(fā)展，螺旋槳的空泡、振動(dòng)和噪聲等問題制約了螺旋槳的發(fā)展，提高單槳的效率也出現(xiàn)了瓶頸，為此國內(nèi)外學(xué)者將目標(biāo)轉(zhuǎn)移到組合螺旋槳的設(shè)計(jì)和研究[1]。組合螺旋槳的出現(xiàn)，不僅提高了推進(jìn)效率，而且有效的改善了空泡和振動(dòng)的發(fā)生。因此，越來越多的學(xué)者致力于組合螺旋槳的研究，包括串列螺旋槳、對(duì)轉(zhuǎn)螺旋槳等。其中，對(duì)轉(zhuǎn)螺旋槳安裝在旋轉(zhuǎn)方向相反的兩個(gè)軸上，而串列螺旋槳在同一軸上裝有前后兩個(gè)旋向相同的螺旋槳。組合螺旋槳能加大槳葉面積，減小單位面積的載荷，且后槳能有效的回收前槳的渦流動(dòng)能，從而提高效率、避免或減輕空化與振動(dòng)的發(fā)生[2-3]。

對(duì)傳統(tǒng)螺旋槳的研究方法主要是依靠模型實(shí)驗(yàn)和理論計(jì)算，實(shí)驗(yàn)周期長(zhǎng)、成本高。采用數(shù)值模擬，不僅能節(jié)省人力物力，還能有效的模擬出實(shí)際螺旋槳的運(yùn)行狀況，因此數(shù)值模擬已成為現(xiàn)階段對(duì)船舶水動(dòng)力性能研究的最重要的方法之一[4]。

本文基于CFD數(shù)值模擬對(duì)螺旋槳進(jìn)行有限元計(jì)算。首先，在不同進(jìn)度系數(shù)下，分析不同湍流模型對(duì)螺旋槳水動(dòng)力性能的影響規(guī)律;同時(shí)，研究螺旋槳的槳葉壓力及流場(chǎng)的變化趨勢(shì)，揭示單槳、對(duì)轉(zhuǎn)槳和串列槳的運(yùn)行特性及敞水性能，為后續(xù)T作奠定理論基礎(chǔ)[3]。

2 控制方程與湍流模型

2.1 控制方程

以船用螺旋槳為研究對(duì)象，周圍的流體可視為不可壓縮流體，即密度p不隨時(shí)間變化。對(duì)于螺旋槳內(nèi)的不可壓縮流體的三維定常流動(dòng)，通常用RANS方程來表達(dá)，其中連續(xù)方程和動(dòng)量方程的表達(dá)式如下[3]：

2.2 湍流模型

本文分別采用standard k-ε、RNC k-ε、RSM和SST k-∞4種湍流模型來計(jì)算螺旋槳在不同的進(jìn)速系數(shù)下的推力系數(shù)Kr、轉(zhuǎn)矩系數(shù)Ko和敞水效率η。考慮到螺旋槳模型曲面空間的復(fù)雜、流場(chǎng)和流動(dòng)旋轉(zhuǎn)特性，本文選取SST k-ω湍流模型，因?yàn)镾ST k-ω湍流模型較RSM湍流模型對(duì)計(jì)算機(jī)的性能要求沒有那么高，同時(shí)能有效真實(shí)地反映實(shí)際情況，計(jì)算速度快、數(shù)值精度較高[3-6]。

2.3 螺旋槳計(jì)算公式

對(duì)螺旋槳通過數(shù)值計(jì)算得到的結(jié)果，應(yīng)用以下公式計(jì)算螺旋槳的推力系數(shù)Kr、扭矩系數(shù)Ko和敞水效率η[3]：

3 計(jì)算模型和網(wǎng)格劃分

3.1 計(jì)算模型

以某船用螺旋槳為對(duì)象，其主要設(shè)計(jì)參數(shù)為：轉(zhuǎn)數(shù)n=450 r/min;螺旋槳直徑D=300 mm;0.7 R處螺距比為P/D=1.3;葉片數(shù)2=4。

為了有效區(qū)分組合螺旋槳和單螺旋槳的各種性能，對(duì)轉(zhuǎn)螺旋槳和串列螺旋槳均由單槳組合而成。其中，對(duì)轉(zhuǎn)螺旋槳的前槳向左旋轉(zhuǎn)，后槳向右旋轉(zhuǎn);串列螺旋槳前后兩槳旋向相同，均為左旋轉(zhuǎn)。圖1分別為螺旋槳、對(duì)轉(zhuǎn)槳和串列螺旋槳的整體模型示意圖。

3.2 網(wǎng)格及計(jì)算域

對(duì)計(jì)算域流場(chǎng)可劃分為靜止域和旋轉(zhuǎn)域兩部分：旋轉(zhuǎn)域?yàn)橹睆?.1 D、長(zhǎng)度3D的小網(wǎng)柱體;靜止域?yàn)殚L(zhǎng)度10D、直徑5D的其余部分。

因螺旋槳形狀復(fù)雜，旋轉(zhuǎn)域因螺旋槳表面曲率較大，因此采用四面體網(wǎng)格劃分;靜止域因結(jié)構(gòu)規(guī)整，采用六面體網(wǎng)格，同時(shí)在槳葉和槳榖處進(jìn)行網(wǎng)格加密，在壁面進(jìn)行邊界層網(wǎng)格處理[2-4]。

對(duì)組合螺旋槳進(jìn)行相同方式進(jìn)行處理。但組合螺旋槳有兩個(gè)旋轉(zhuǎn)域，需要通過interior對(duì)前后兩槳的旋轉(zhuǎn)域進(jìn)行連接，旋轉(zhuǎn)域和靜止域之間的交界面采用interface聯(lián)接。

4 數(shù)值計(jì)算與分析

4.1 單螺旋槳敞水性能分析

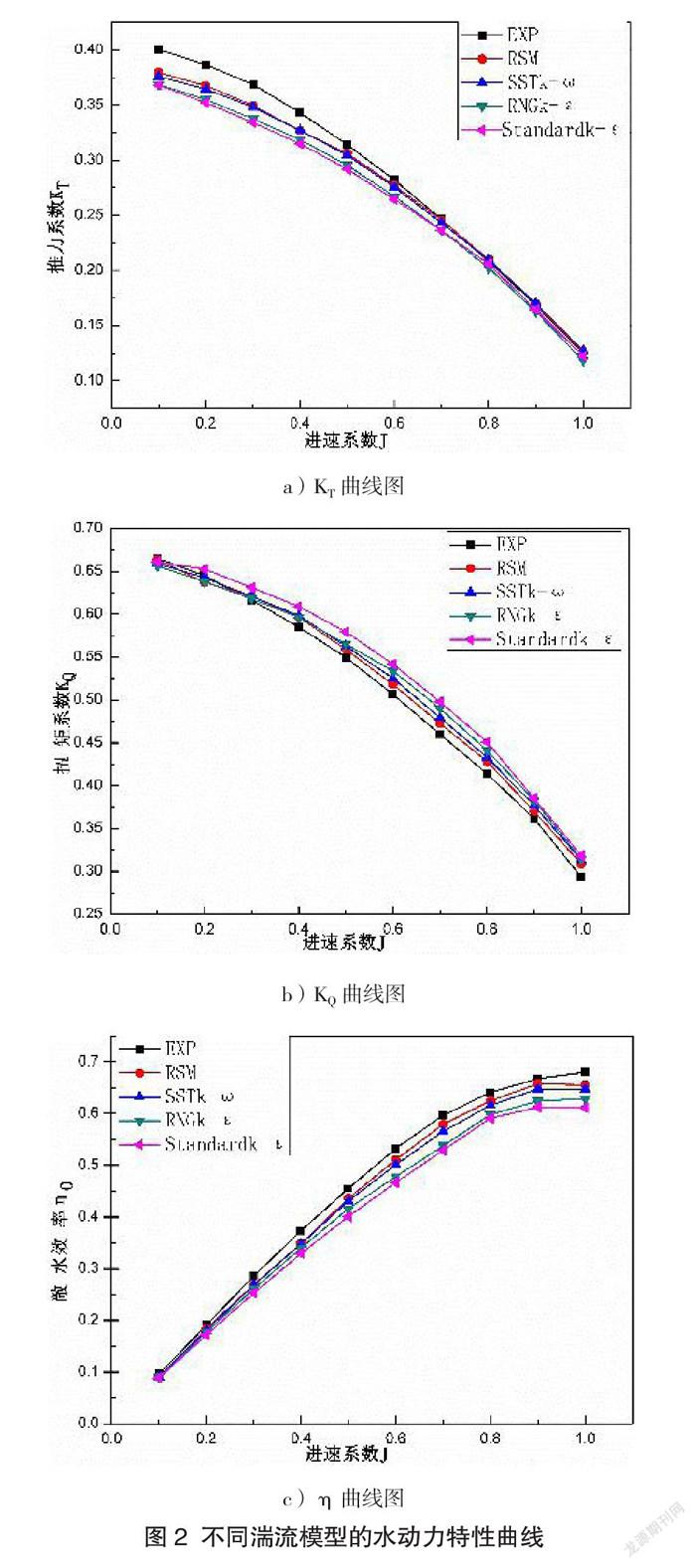
本文選取Standard k-ε、RNC k-ε、RSM和SSTk-∞4種湍流模型進(jìn)行數(shù)值計(jì)算。螺旋槳的轉(zhuǎn)速為450r/min，在進(jìn)速系數(shù)0.1-1.0范圍內(nèi)計(jì)算的數(shù)值結(jié)果與實(shí)驗(yàn)值相比較，并繪制出在不同湍流模型的水動(dòng)力性能曲線圖，如圖2所示。

（1）從Kr和Ko曲線圖可知：4種湍流模型得出的KT與實(shí)驗(yàn)值誤差較小，當(dāng)J過小或者過大時(shí)，誤差增大;10Ko隨著J逐漸增大，而模擬計(jì)算的Ko與實(shí)驗(yàn)值誤差與J成正比。總體上說，RSM湍流模擬效果與實(shí)驗(yàn)相吻合，Standard k-ε湍流模型與實(shí)驗(yàn)誤差較大;

（2）從η曲線圖可看出：實(shí)驗(yàn)值均大于湍流模型的計(jì)算值;在不同J值下，RSM湍流模型和SST k-ω湍流模型邯曲線與實(shí)驗(yàn)值相吻合且精度高。

綜上分析可得，與實(shí)驗(yàn)值的敞水效率吻合度最好的是RSM和SST k-ω湍流模型，但RSM湍流模型對(duì)計(jì)算機(jī)的配置和運(yùn)行性能的要求非常高，同時(shí)計(jì)算所花費(fèi)的時(shí)間長(zhǎng)，因此最佳湍流模型選擇SST k-ω湍流模型。

4.2 對(duì)轉(zhuǎn)螺旋槳數(shù)值驗(yàn)證

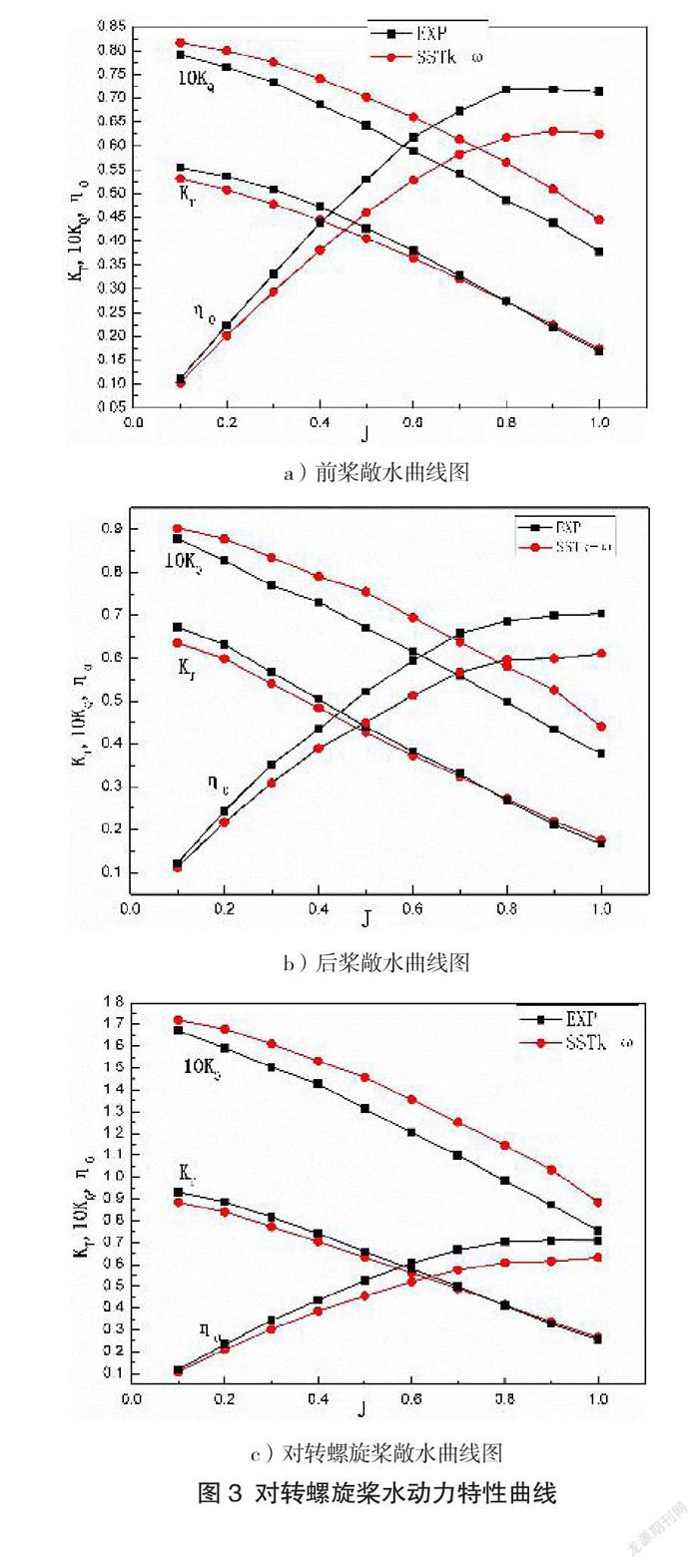
對(duì)轉(zhuǎn)螺旋槳的前、后槳扭矩大小相當(dāng)，旋轉(zhuǎn)方向相反，轉(zhuǎn)速均為450 r/min。基于SST k-ω湍流模型，進(jìn)速系數(shù)J在0.1-1.0之間對(duì)轉(zhuǎn)槳進(jìn)行數(shù)值模擬，并繪制數(shù)值模擬和實(shí)驗(yàn)數(shù)據(jù)的水動(dòng)力特性曲線，如圖3所示。由圖3可知，對(duì)轉(zhuǎn)槳前、后槳的Kr曲線和Ko曲線與實(shí)驗(yàn)值均相吻合，且10Ko隨著J的增大而減小。經(jīng)過分析可知：后槳受前槳尾流的影響，使得在同一進(jìn)度系數(shù)J下，前槳Ko的誤差小于后槳的誤差。

從圖3c）可以看出：對(duì)轉(zhuǎn)螺旋槳的推力系數(shù)Kr總體模擬效果都比較好，但10Ko的誤差隨著J的增大而增大，整體數(shù)據(jù)均大于實(shí)驗(yàn)值，而效率η均小于實(shí)驗(yàn)值。

由上可知，基于CFD數(shù)值模擬得出的結(jié)果與實(shí)驗(yàn)值吻合度較高，且滿足精度要求。

4.3 串列螺旋槳數(shù)值驗(yàn)證

串列螺旋槳前、后兩槳的旋轉(zhuǎn)方向相同，且轉(zhuǎn)速也均為450 r/min。基于SST k-ω湍流模型在進(jìn)速系數(shù)J為0.2-1.0的范圍進(jìn)行數(shù)值計(jì)算，并將得到的結(jié)果繪制水動(dòng)力特性曲線，同時(shí)與實(shí)驗(yàn)值進(jìn)行比較，如圖4所示：

從圖4可以看出：在進(jìn)速系數(shù)J=0.2-1.0范圍內(nèi)，串列螺旋槳的KT曲線、KQ曲線和η曲線的計(jì)算值和實(shí)驗(yàn)值的變化趨勢(shì)基本吻合。其中，數(shù)值計(jì)算得到的KT和η小于實(shí)驗(yàn)值，但10KQ值大于實(shí)驗(yàn)值，同時(shí)從圖中可以看出，KT、KQ和η的誤差與進(jìn)速系數(shù)J成正比關(guān)系，最終結(jié)果與實(shí)驗(yàn)值吻合度較高，驗(yàn)證了數(shù)值模擬方案的可行性。

4.4 組合槳數(shù)值驗(yàn)證

選取普通螺旋槳、對(duì)轉(zhuǎn)槳和串列槳進(jìn)行數(shù)值計(jì)算，按其結(jié)果繪制功率系數(shù)水動(dòng)力特性曲線，如圖5所示。

由圖5可知：對(duì)轉(zhuǎn)螺旋槳和串列螺旋槳的效率比單槳的效率高。其中，對(duì)轉(zhuǎn)螺旋槳的效率最高，串列螺旋槳次之。在BP=6-255范圍內(nèi)，對(duì)轉(zhuǎn)螺旋槳比普通螺旋槳效率提高了7.28%-15.07%，串列螺旋槳比對(duì)轉(zhuǎn)螺旋槳效率提高了2.68%-9.79%。

4.5 螺旋槳尾流分析

采用CFD數(shù)值計(jì)算模擬方法，能真實(shí)有效地反應(yīng)出螺旋槳處的流場(chǎng)情況。為了更清晰的分析單槳和組合槳的尾流情況，選取同一進(jìn)度系數(shù)J=0.7進(jìn)行分析，如圖6所示。

由圖6可知：?jiǎn)温菪龢奈擦魍鈴酱笥诼菪龢闹睆剑M合螺旋槳尾流外徑小于螺旋槳的直徑;單槳尾流直徑與進(jìn)度系數(shù)成正比關(guān)系，而組合槳前、后槳相互影響，其后槳吸收前槳的軸流速度與渦流能量，使得尾流外徑小于螺旋槳的直徑，組合螺旋槳能有效提高螺旋槳的性能與能量的利用率。

5 結(jié)論

本文基于CFD數(shù)值模擬對(duì)螺旋槳進(jìn)行有限元計(jì)算.首先，在不同進(jìn)度系數(shù)下，分析不同湍流模型對(duì)螺旋槳水動(dòng)力性能的影響規(guī)律，同時(shí)，研究螺旋槳的槳葉壓力及流場(chǎng)的變化趨勢(shì)，揭示單槳、對(duì)轉(zhuǎn)槳和串列槳的運(yùn)行特性及敞水性能，得出以下結(jié)論：

（1）采用4種湍流模型對(duì)單螺旋槳進(jìn)行有限元計(jì)算，RSM湍流模型和SST k-ω湍流模型表現(xiàn)出明顯的優(yōu)勢(shì)，說明有限元計(jì)算對(duì)分析螺旋槳的水動(dòng)力特性具有可行性和準(zhǔn)確性;

（2）通過對(duì)單槳和組合槳的數(shù)值模擬結(jié)果進(jìn)行分析，在功率系數(shù)相同的條件下，組合螺旋槳其敞水效率與單槳相比，體現(xiàn)出明顯的優(yōu)勢(shì);

（3）通過對(duì)尾流分布分析可知：對(duì)于組合槳而言，后槳能有效的吸收前槳的軸向速度和渦流能量，同時(shí)切向速度對(duì)流體的影響減小，從而流過螺旋槳槳葉的動(dòng)量增加，使得前槳的尾流外徑減小，螺旋槳的推力也隨之增加，提高了對(duì)轉(zhuǎn)螺旋槳推進(jìn)性能;同時(shí)，組合螺旋槳負(fù)荷較輕，在一定程度上減少了振動(dòng)和噪聲。

參考文獻(xiàn)

[1]楊美紅，李鐵驪，胡俊明，林焰等.基于CFD法的對(duì)轉(zhuǎn)螺旋槳敞水性能參數(shù)匹配研究[J]船舶1。程，2016，39（ ll）：42-46.

[2]王國強(qiáng)，董世湯.船舶螺旋槳理論與應(yīng)用[M].哈爾濱：哈爾濱]一程大學(xué)出版社，2005：383-396.

[3]王聲森.基于CFD的某船對(duì)轉(zhuǎn)槳側(cè)推器的性能預(yù)測(cè)[D].江蘇科技大學(xué)，2019.

[4]胡俊明，李鐵驪，林焰，紀(jì)卓尚等.基于RANS法的B系列對(duì)轉(zhuǎn)螺槳旋敞水性能數(shù)值模擬[J].大連理]‘大學(xué)學(xué)報(bào)，2017，57（2）：148-156

[5]王展智，熊鷹，齊萬江.對(duì)轉(zhuǎn)螺旋槳敞水性能數(shù)值預(yù)報(bào)[J]華中科技大學(xué)學(xué)報(bào)，2012，40（ 11）：77-80.

[6]曾攀.有限元分析基礎(chǔ)教程[M].北京：清華大學(xué)出版社，2008.