縱橫向運動耦合時車輛狀態估計算法研究

周興林，袁琛琦，盛中華

（武漢科技大學汽車與交通工程學院，湖北 武漢430065）

1 引言

隨著車輛底盤穩定性電控系統的不斷發展，車輛行駛狀態信息的測量與獲取顯得尤為重要。車輛的主動安全性能可以通過系統識別運動過程中的動力學狀態和參數來調整相應的控制策略而得以提高。

作為車輛狀態估計的基本方法，經典卡爾曼濾波估計方法［1］在車輛狀態參數估計的問題上應用廣泛，但是該方法的應用針對線性系統。而后為了解決非線性系統的狀態參數估計問題，在經典的線性卡爾曼濾波基礎上擴展卡爾曼濾波（extended kalman filter，EKF）估計算法被提出，它通過對非線性函數進行線性化來消除高階分量。文獻［2］建立了整車動力學模型，并應用卡爾曼濾波觀測器對汽車的質心側偏角和橫擺角速度進行了估計。文獻［3-4］相繼應用擴展卡爾曼濾波算法在車輛狀態參數估計領域做出了突出貢獻，但以上研究都是從縱向、側向和垂向三個層面獨立展開，而在實際行駛狀態下，車輛的各項運動響應存在耦合作用的特征。文獻［5］較早針對車輛縱橫向動力學耦合問題和輪胎力耦合問題進行了研究，然而，目前我國對于車輛耦合動力學控制的研究還較少。

另一方面，國內外對車輛狀態參數的估計大都針對開環系統，車輛的操縱性評價是十分復雜的問題，研究駕駛員在環仿真系統更接近車輛在實際行車條件下的情況，實用價值更高［6］。文獻［7］對駕駛員轉向特性的分類和在線辨識進行了實驗研究。20世紀中期以來，多種不同種類的駕駛員模型被提出，預瞄控制方式相對于其它控制方式而言，更符合實際駕駛經驗，能夠獲得更好的期望路徑跟蹤效果，且能夠體現駕駛員實際操控車輛時的預瞄作用［8］。因此，本文基于預瞄最優曲率駕駛員模型，建立駕駛員-車輛閉環仿真系統，并結合擴展卡爾曼濾波理論對車輛的縱向速度、橫向速度和橫擺角速度進行測量。

2 車輛動力學模型

2.1 車輛縱橫向動力學耦合模型

結合車輛縱向受力簡圖和車輛單軌模型橫向受力俯視圖，得到車輛縱橫向受力俯視圖［9］，如圖1所示，oxy為固定于車身的車輛坐標系，車輛重心c.g.所在點o為坐標原點，x坐標軸沿車輛縱軸方向，y軸垂直于車輛縱軸方向，OXY為一個固定于地面的慣性坐標系。

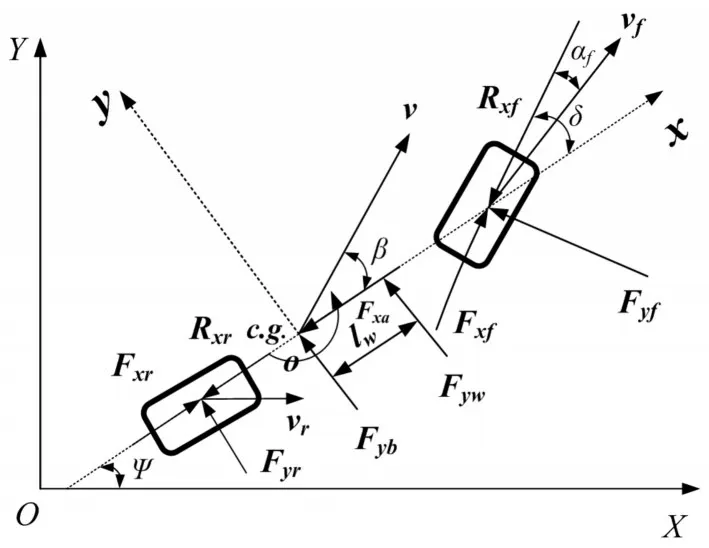
圖1 車輛縱橫向受力俯視圖Fig.1 Top View of the Longitudinal and Lateral Forces of the Vehicle

根據牛頓運動定律，作用在車輛上的外力之和等于線動量變化率；作用在車輛上的外力矩之和等于角動量變化率。所以：

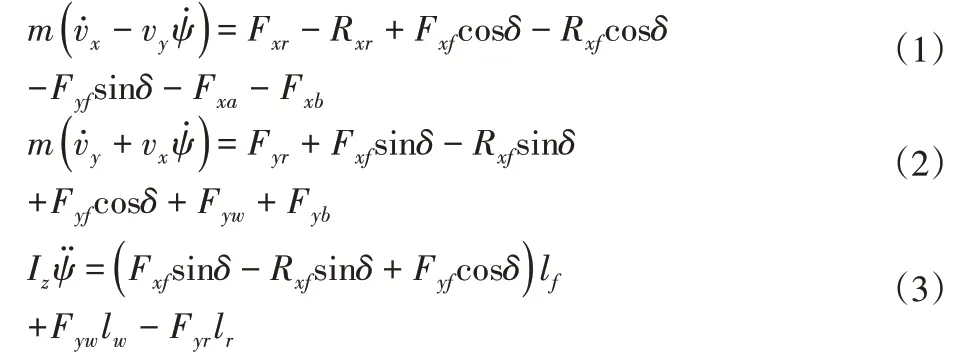
假設路面沒有側傾和俯仰，車輛不受橫向滾動阻力的影響，且相對風速在縱向和橫向上為零，假設δ較小，前、后輪的附著率相等，則簡化后的模型公式為：

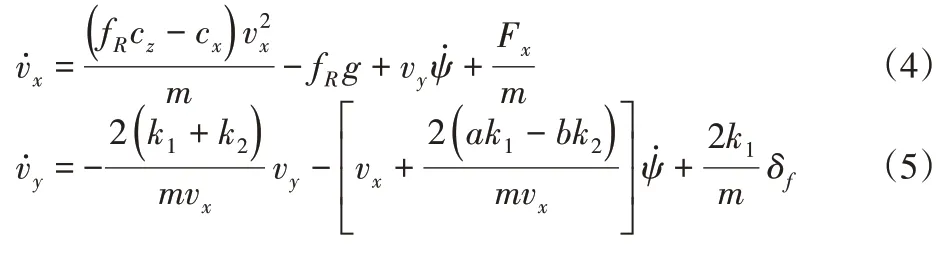
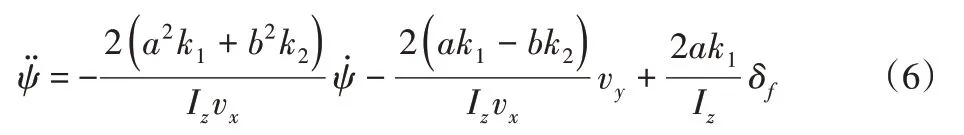
式中：vx、vy、車輛的縱向車速、側向車速和橫擺角速度；m、Iz—車輛質量和繞z軸轉動時的轉動慣量；a、b、k1、k2—質心到前輪的距離、質心到后輪的距離、前輪輪胎的側偏剛度和后輪輪胎的側偏剛度；g、fR、cx/cz—重力加速度、滾動阻力系數和比例系數；Fyw、Fyb、Fxf、Fxr、Fyf、Fyr、Ryf、Ryr、δf—側向風力、重力沿側向分量、地面作用在前輪上的縱向力、地面作用在后輪上的縱向力、地面作用在前輪上的橫向力、地面作用在后輪上的橫向力、地面作用在前輪上的滾動阻力、地面作用在后輪上的滾動阻力和前輪轉向角。

2.2 輪胎模型的選擇

采用Dugoff輪胎模型能夠用于縱滑側偏聯合工況下的縱向力和側向力的求解，忽略回正力矩的作用，Dugoff輪胎模型中的輪胎牽引力Fxi和輪胎側向力Fyi可表示為：

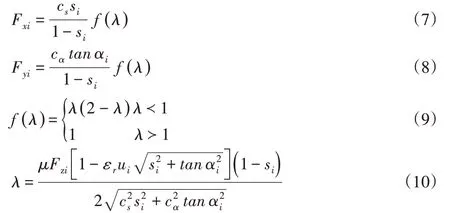
滑移率在制動和驅動下計算公式：

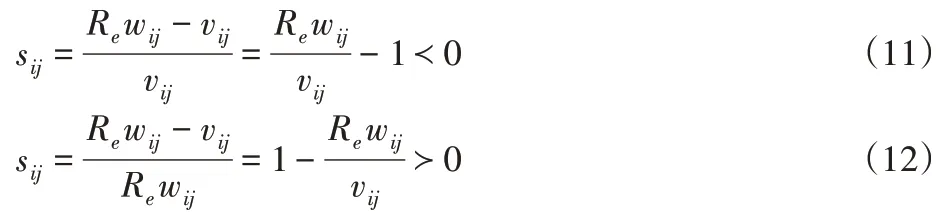
車輛的垂直載荷計算公式：

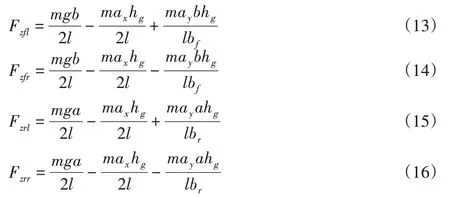
式中：λ—輪胎動態參數；μ—名義路面附著系數；εr—路面附著縮減系數；cs和cα—輪胎的縱向剛度和側向剛度；Fzi—輪胎垂向載荷；sij—縱向滑移率；i、j—輪胎位置，i—前輪或后輪，j—左輪或右輪；hg—質心高度；ax和ay—縱向加速度和側向加速度；l—輪距；bf和br—前輪輪距和后輪輪距。

2.3 基于加速度反饋的預瞄最優曲率駕駛員模型

建立一個能反映車輛各種行駛工況的駕駛員模型是閉環控制系統中的一個關鍵問題。大角度單點預瞄最優曲率模型，如圖2所示。經過T時間：y(t+T)=y(t)+Ty˙(t)+0.5T2y¨(t)，根據“最小誤差原則”，駕駛員選擇最優軌跡曲率1R*（R*為最優轉彎半徑），車輛在經過預瞄距離ld之后，橫向位置y（t+T）與預期軌跡f（t+T）接近一致［10］。

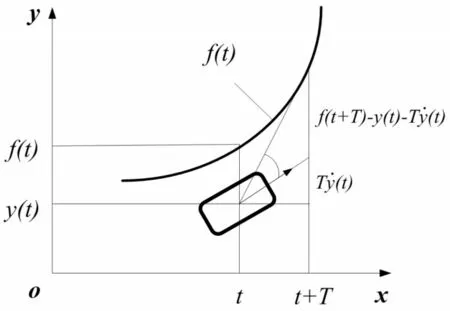
圖2 大角度單點預瞄最優曲率模型Fig.2 Large Angle Single Point Preview Optimal Curvature Model

根據離心運動狀態以及最小誤差軌跡跟蹤原則，得到最優橫向加速度：

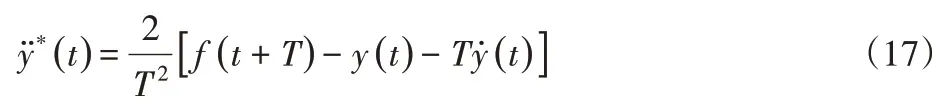
最優曲率為：

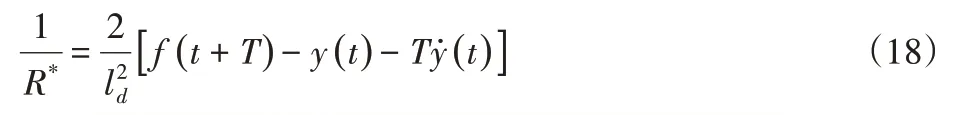
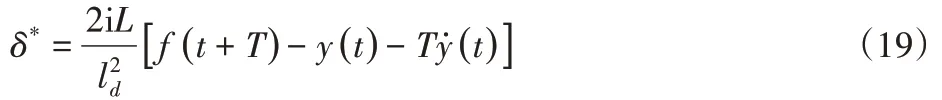
在實際道路上行駛時，Gay—車輛的橫向加速度對方向盤轉角的穩態增益，y¨*（t）—最優橫向加速度，達到最優橫向加速度應該施加的理想方向盤轉角為：

對最優方向盤轉角進行修正來計算實際的方向盤轉角，即：

式中：δ0—考慮駕駛員生理限制后的方向盤轉角，1+ths和—車輛轉向盤慣性滯后環節和駕駛員神經系統反應滯后環節，th和td—轉向盤慣性滯后時間常數和神經系統反應滯后時間常數。運用δ0進行方向控制時，車輛實際和理想側向加速度之間存在偏差，此時對轉向盤轉角進行修正，修正量為：

式中：Δδ—車輪轉角增量；δ0和修正量Δδ的和等于駕駛員模型最后決策出的方向盤轉角δ。

基于加速度反饋的預瞄最優曲率駕駛員模型圖，f（t+T）—預瞄時間為T的道路輸入，道路輸入結合側向位移y（t）和實際側向速度y˙（t）兩個反饋信號可以得到理想的側向加速度，經過校正環節、神經系統反應滯后和轉向盤慣性滯后環節獲得實際的方向盤轉角作為車輛模型輸入，如圖3所示。

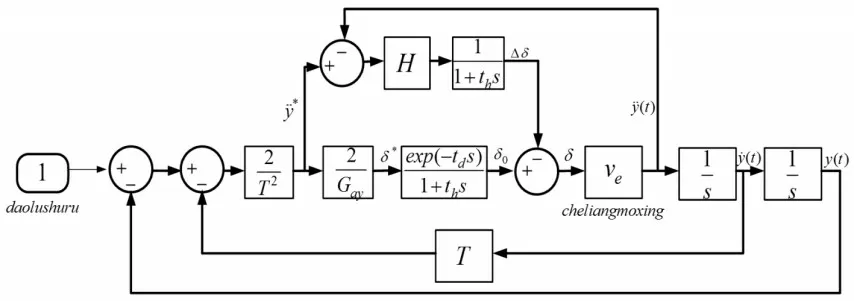
圖3 基于加速度反饋的預瞄最優曲率駕駛員模型Fig.3 Pre-pumped Optimal Curvature Driver Model Based on Acceleration Feedback

為實現車輛在復雜工況下縱橫向運動耦合時車輛的狀態參數估計，在車輛動力學仿真軟件MATLAB/Simulink環境下建立駕駛員-車輛閉環整車系統，整車系統包括車身模型和輪胎模型。其中車身模型由縱向和橫向運動耦合模塊組成，輪胎模型由側偏角模塊、車輪旋轉運動模塊、滑移率模塊等模塊組成。

3 基于擴展卡爾曼濾波的車輛狀態估計

擴展卡爾曼濾波（EKF）是非線性系統的一種無偏最小方差估計方法。非線性系統的狀態空間方程可表示為：

狀態方程：

觀測方程：

而在實際應用中，由于測量噪聲vk和過程噪聲wk不能在每個時刻以特定步長確定，所以非線性系統可以近似表示為：

狀態方程：

測量方程：

擴展卡爾曼濾波估計方程推導公式如下：

初始化濾波器：

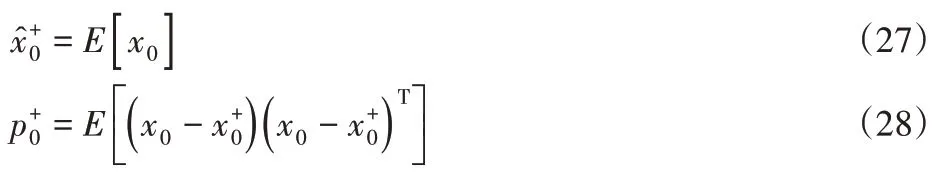
雅克比矩陣：

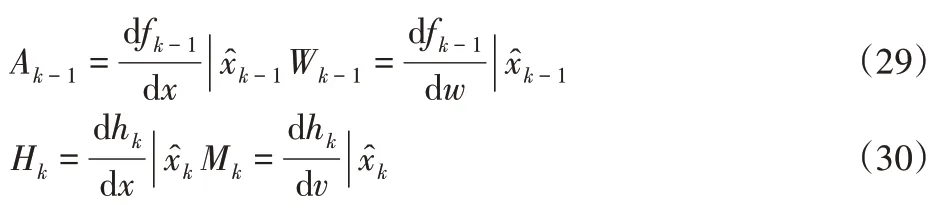
算法可以分為預測和校正兩個階段：

狀態估計和估計誤差協方差的時間更新方程（預測）為：

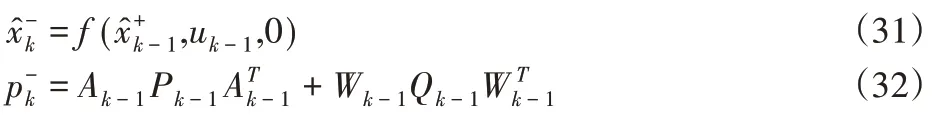
狀態估計的測量更新和估計誤差協方差的更新（校正）為：

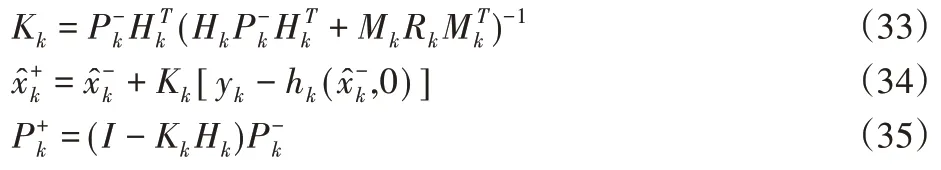
Kk為卡爾曼濾波器增益，選擇車輛的縱向速度、橫向速度和橫擺角速度作為估計器的狀態變量。

狀態方程表達式：

觀測方程表達式：

式中：x（t）、u（t）、w（t）和v（t）—狀態變量、控制變量、過程噪聲和測量噪聲，噪聲為相互獨立的高斯白噪聲；Qk和Rk—w（t）和v（t）的協方差矩陣。

根據上述分析，在MATLAB/Simulink中建立如圖4所示的車輛狀態參數估計模型。

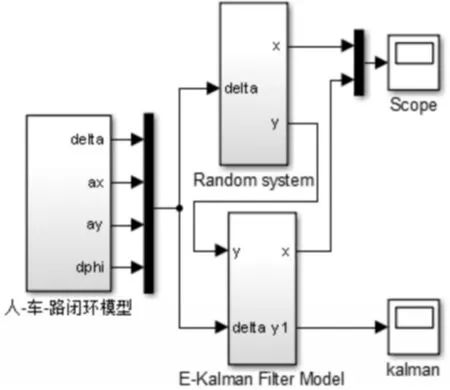
圖4 車輛狀態參數估計模型Fig.4 Vehicle State Parameter Estimation Model

4 仿真實驗驗證

在Matlab/Simulink軟件下對所提算法進行仿真驗證，所采用的車輛主要參數為m=2100kg，車輪半徑R=0.31m，繞z軸的轉動慣量Iz=2549kg·m2，輪胎轉動慣量Iw=2.1kg·m2，前軸到質心的距離a=1.256m，后軸到質心的距離b=1.368m，質心高度hg=0.7m，空氣阻力系數C=0.34，滾動阻力系數fR=0.02，控制校正增益C0=0.2282，穩態增益Gay=4.3821。仿真中，路面附著系數設為0.5，預瞄時間T和駕駛員模型參數在仿真過程中被多次調整，在縱向車速為30m/s時，預瞄時間T為0.3s。估計器協方差p0=eye（3）*1，過程噪聲協方差Q=eye（3）*0.00001，測量噪聲協方差R=eye（3）*100000，估算初值賦值x1=（30，0，0）。為模擬汽車的蛇形路徑行駛工況，按照穿桿試驗的要求，設定相應頻率和振幅的正弦道路作為系統輸入。

圖5中估計結果存在一定的誤差，誤差主要集中在波峰和波谷處，但估計值與仿真值的變化趨勢具有較高的吻合度，估計值穩定性較好且最大誤差不超過5%，結果表明，基于擴展卡爾曼濾波的估計模型可以更好地估計蛇形行駛條件下車輛的行駛狀態。在蛇形工況開始時，車輛和駕駛員存在響應滯后，而道路突然過渡到正弦形式，此時車輛行駛軌跡與預期軌跡有較大的差異，隨著車速趨于穩定，誤差也越變越小。

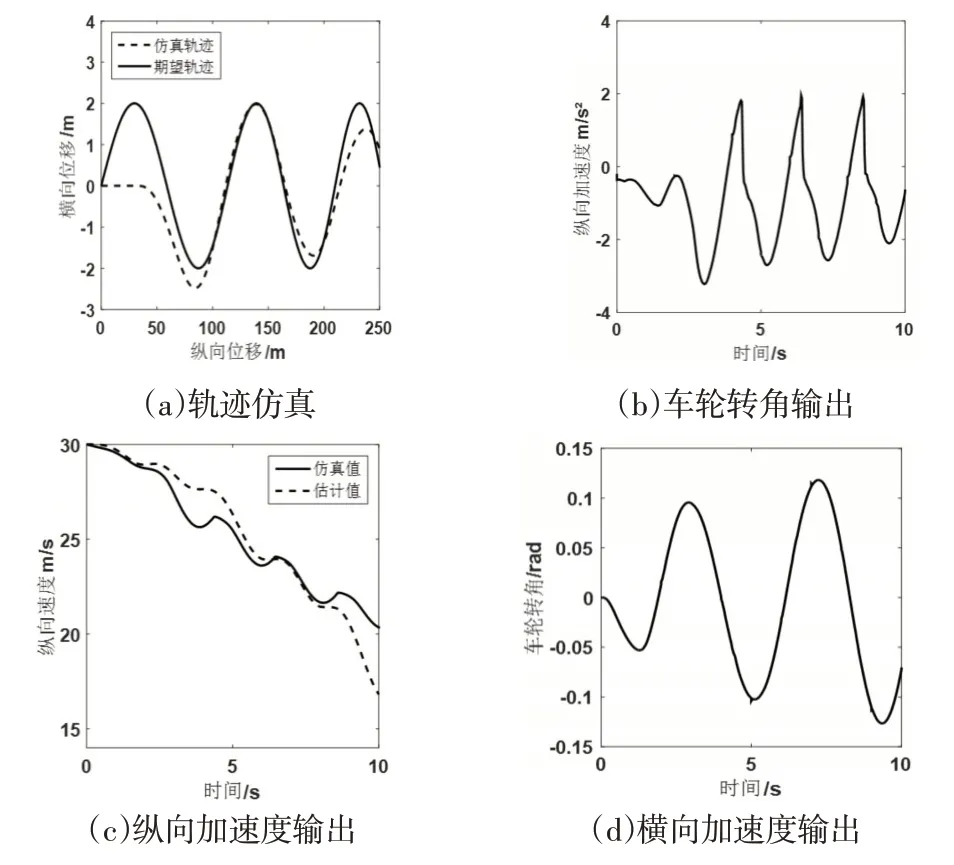
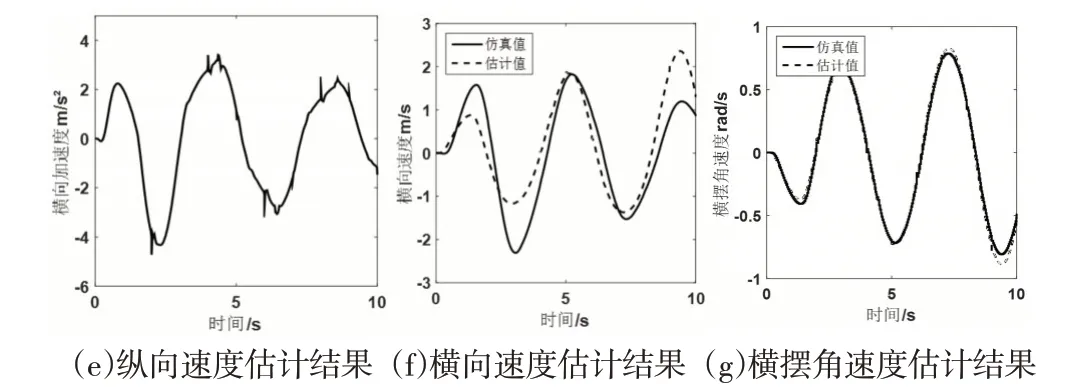
圖5 蛇形工況下車輛的行駛狀態Fig.5 Driving State of the Vehicle Under Serpentine Conditions

導致誤差的原因為加速度方向變化對模型精度有影響，而在縱橫向耦合運動條件下，車輛輪胎垂直載荷的變化也受諸多因素影響，為使問題簡化載荷分配計算并不精確；另一方面，并未考慮車身的俯仰和側傾運動。

5 結論

本文基于縱向和橫向運動耦合模型，建立了駕駛員-車輛閉環仿真系統，應用擴展卡爾曼濾波技術對車輛的行駛狀態參數進行了估計。在數據處理軟件MATLAB/Simulink下，得到如下研究結論：

（1）駕駛員-車輛閉環仿真模型考慮了車輛縱橫向耦合運動作用特征，將道路模型輸入轉換為車輛前輪轉角作為閉環模型的初始輸入，對研究“人-車”閉環控制動力學仿真具有重要意義。

（2）通過對比估計模型結果和車輛動力學模型的仿真結果，表明該算法可以較準確地估計車輛在縱橫向耦合運動條件下的狀態變量，可以準確地反映車輛實際狀態的發展趨勢。