混凝土泵車臂架可靠度分析

黃會榮，張 希

（西安建筑科技大學機電工程學院，陜西 西安710055）

1 引言

混凝土泵車施工靈活高效，廣泛應用在工程建設中，其核心部件是臂架［1］。目前對臂架結構強度的研究是以材料力學為基礎，根據材料強度極限采用安全系數法進行校核。王碧琨創建了一個37米泵車臂架模型，并進行了靜力分析和模態分析，得到了臂架應力云圖和模態振型圖，指出了臂架的薄弱地方，并提出了后續的優化方案［2］。朱俊輝采用有限元技術，分析了某款泵車臂架結構的強度和剛度性能，得出了不同工況下臂架的應力分布和變形情況［3］。王斌華等通過力學分析找出了泵車工作時的危險工況和經典工況，并在危險工況下對該泵車整體結構進行了有限元分析［4］。這些研究方法均將設計參數作為常量進行分析，卻忽略了各種誤差產生的影響。

結構可靠度分析將臂架結構尺寸、材料參數以及載荷等作為設計參數，研究臂架在靜力條件下各參數對臂架位移和應力的影響。這種方法將影響臂架位移和應力的參數看作不確定量，研究這些變量對臂架靜力分析的影響程度，進而提高臂架設計的準確度和可靠度，達到滿足強度又節省材料的目的。本文使用了可靠度分析法，利用APDL語言完成參數化建模，結合PDS模塊中的兩種計算方法，在置信水平95%的條件下對泵車臂架進行了結構可靠度分析。首先利用蒙特卡羅法得到了臂架結構的可靠度。進一步做了靈敏度分析，以找出影響臂架位移與應力的設計參數。最后使用響應面法分析了兩組關聯設計參數共同作用下的臂架位移和應力的擬合響應面，為后續臂架結構的設計與改進提供一些參考依據。

2 結構可靠度介紹與分析步驟

2.1 結構可靠度介紹

結構的可靠度是指，結構在規定的時間內與指定的條件下，完成結構預定功能的能力［5］。實際工程中，結構的設計模型不完善、材料屬性不真實、施加載荷不精準等均有不確定性，這些因素隨機的變化將會影響整個結構的可靠度。為了深入研究結構的可靠度，引入數學方法表述不確定因素和結構可靠度之間的關系，使用概率來表示結構實現預定功能的能力，構建的結構功能函數如下：

式中：Z—結構功能函數；X1,X2,X3,…,Xn—結構可靠度研究中的各個隨機不確定因素。

結構功能函數可用圖1表示，由圖可知，Z＜0時結構失效；Z=0時結構極限狀態；Z＞0時結構安全可靠。

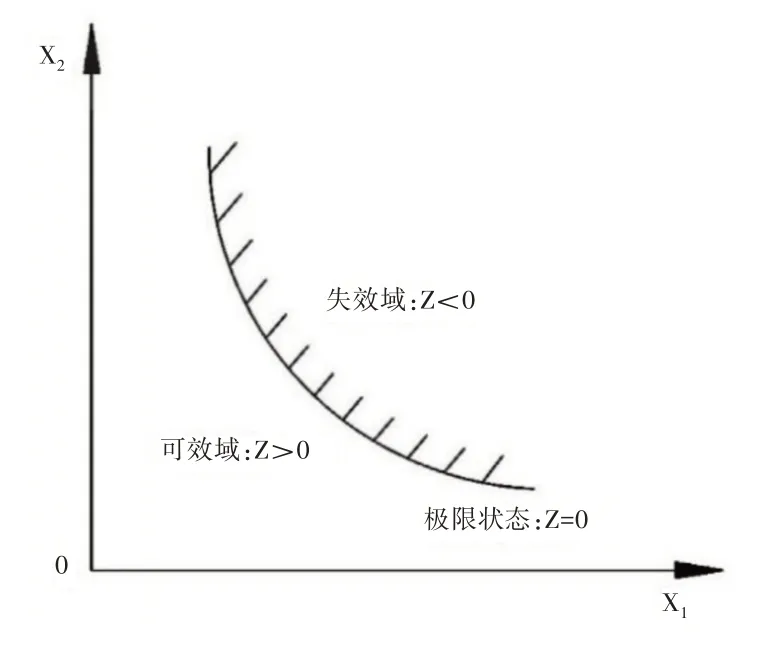
圖1 結構極限工作狀態Fig.1 The Ultimate Working State of the Structure

2.2 結構可靠度分析步驟

利用PDS模塊進行可靠度分析，詳細分析步驟如下［6］：

（1）制定分析文件。采用APDL語言在ANSYS中制定分析文件，其順序如下：①參數化建模，確定臂架三維模型和尺寸，進行參數化編寫所有的結構尺寸、彈性模量、密度、載荷等。②劃分有限元網格，定義單元類型后對臂架模型進行網絡劃分，施加固定約束與載荷后進行靜力求解。③后處理求解，獲得應力與位移結果，為后續分析做準備。

（2）將創建好分析文件導入ANSYS的PDS模塊中，進行初始化加載運行。

（3）根據所要研究的臂架模型確定輸入和輸出參數，并選擇選擇蒙特卡羅法進行分析，從而得到臂架結構的失效概率和可靠度。

（4）進行靈敏度分析，得到影響臂架應力和位移的設計參數，并找出主要影響參數著重分析。

（5）采用響應面法分析，得到兩組關聯參數對臂架位移與應力變化的響應面。

3 建立臂架參數化模型

以某型號混凝土泵車臂架為例進行實體建模，選擇臂架受力最大的第一節，對其進行適當簡化，建立了臂架的全參數化實體模型，并得到圖2所示尺寸設計參數圖。

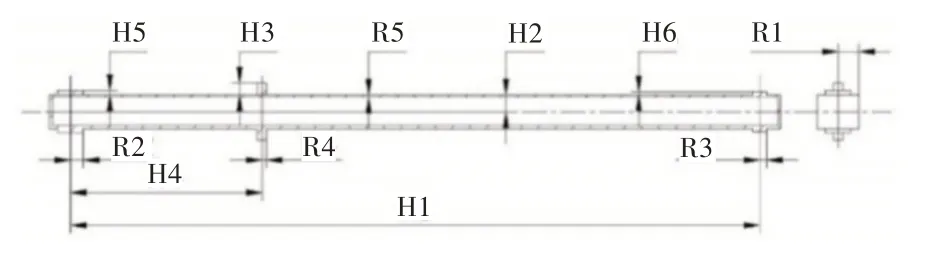
圖2 臂架尺寸設計參數Fig.2 Dimension Design Parameters of the Boom

這些設計參數可以歸為三類，分別是尺寸、材料和載荷參數，整理得到的變量參數，如表1所示。

表1 各個變量設計參數Tab.1 Design Parameters of Each Variable

混凝土泵車臂架使用WELDOX900E型高強度鋼制造，其屈服強度為900MPa，彈性模量為2.1×1011Pa，材料密度為7850Kg/m3,泊松比為0.3［7］。單元類型SHELL181殼單元，施加約束為轉臺與臂架的鉸接約束和液壓缸與節臂的支撐約束，施加載荷主要是臂架的自重和在泵送過程中管道內混凝土的自重，經計算等效載荷大小為301200N。進行單元網絡劃分，劃分的單元數量為12124，節點數量為24320并施加約束與載荷，如圖3所示有限元模型。

圖3 臂架網絡劃分及約束受力Fig.3 Network Division and Constraint Force of the Boom

4 臂架的蒙特卡羅法可靠度分析

4.1 蒙特卡羅法介紹

蒙特卡羅法可以定義幾千個輸入參數，適合分析大型復雜結構，并且仿真循環次數越多，得到的可靠度分析結果越接近真實值［8］。PDS模塊中含有直接蒙特卡羅法和拉丁超立方法（LHS）法兩種抽樣方法。兩者相比，LHS法具有記憶性，可以避免重復抽樣，因此選擇LHS法。

查閱資料得知眾多零部件的幾何參數、材料參數、載荷參數等都服從正態分布N(μ,σ2)，工程中材料的強度標準值采用概率分布的0.05。將表1中各變量（泊松比除外）值作為輸入參數，將位移與應力變量作為輸出參數，如表2所示。

表2 各變量輸出參數Tab.2 Output Parameters of Each Variable

4.2 可靠度結果分析

為確定樣本是否滿足分析要求，查看隨機輸入參數的直方圖。經過1000次循環計算后，選取尺寸變量H1和R3，生成圖4所示的抽樣直方圖。由圖可知，這兩個參數抽樣分布曲線較為平滑，接近正態分布，故此次抽樣符合分析條件。

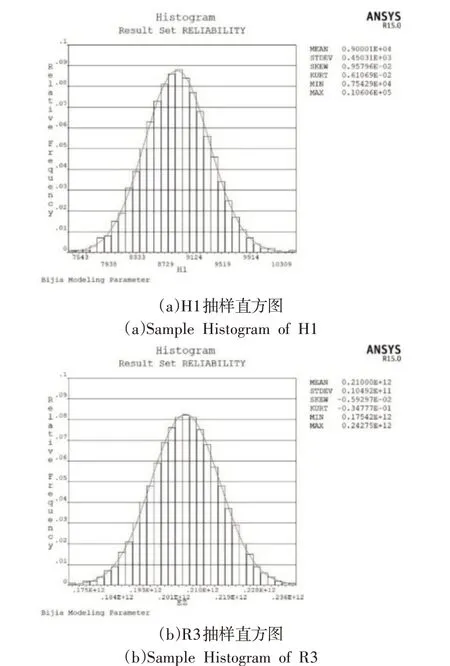
圖4 部分參數抽樣直方圖Fig.4 Sample Histogram of Partial Parameters

查看分析結果，得到臂架位移NMAX平均值為0.191m，臂架應力SMAX平均值是272.41MPa，均在材料許用值內。臂架位移NMAX的累積分布函數如圖5（a）所示，應力SMAX的累積分布函數如圖5（b）所示。可以看出位移NMAX的可靠度為1，應力SMAX的可靠度也為1，表明該臂架結構可靠，設計合理，符合施工使用要求。

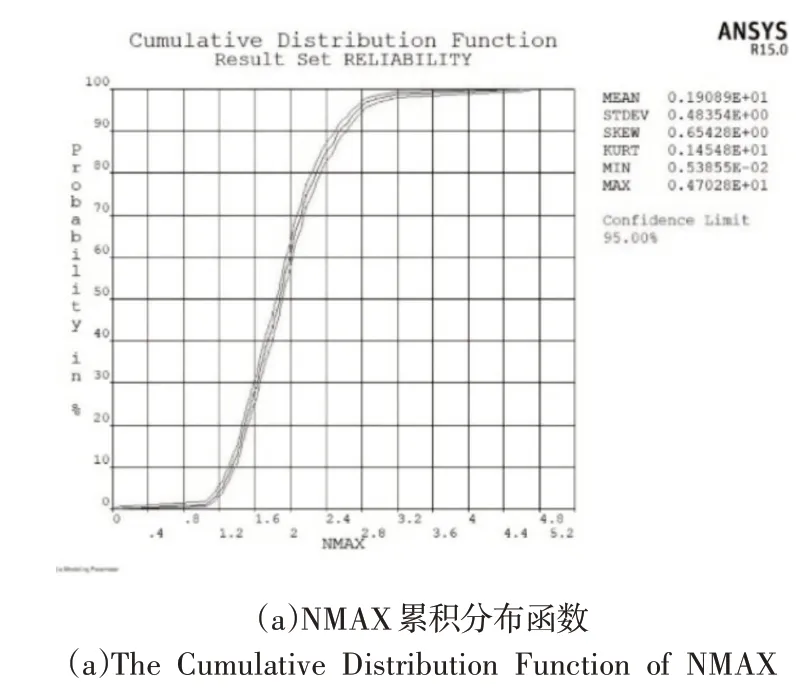
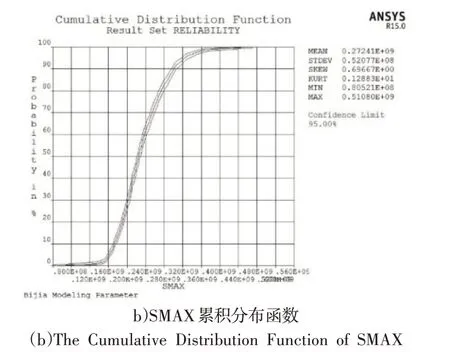
圖5 位移和應力累積分布函數圖Fig.5 The Cumulative Distribution Function of Displacement and Stress

5 臂架的靈敏度分析

不同的臂架結構設計參數對結構可靠度的影響程度是不一樣的。某些參數變化時對可靠度影響較大，稱其為敏感因素，因此在結構設計應精確取值，產品制造中應保證加工精度；反之，某些參數的變化對結構可靠度影響十分微弱，稱其為不敏感因素，分析時為了提高計算效率，簡化結構狀態函數，就可以把這些變量當作定值對待［9］。對臂架進行靈敏度分析，為臂架結構設計、加工制造和產品維護給予理論性指導意見。

如圖6所示，由NMAX餅圖得知，臂架長度H1的靈敏度為正，表明當臂架長度增大時，臂架的位移會顯著增大；臂架寬度的一半R1的靈敏度為負，則當臂架寬度增大時，臂架的位移會逐漸減小。其他的結構設計參數如臂架之間鉸接點半徑R3和寬度H6以及臂架承受壓力YL的靈敏度均為正，均會使臂架的位移增大，從而影響混凝土澆筑位置的精確度，因此在結構設計及后續的加工制造只能怪中需著重控制這些參數。還有一些設計參數如臂架液壓缸支撐點與鉸接點距離H4、材料的彈性模量EZ、臂架高度H2以及臂架板厚度R5的靈敏度均為負，表明適當的增大這些參數的設計值可以達到減小臂架位移的目的，進而提高混凝土的澆筑精度。

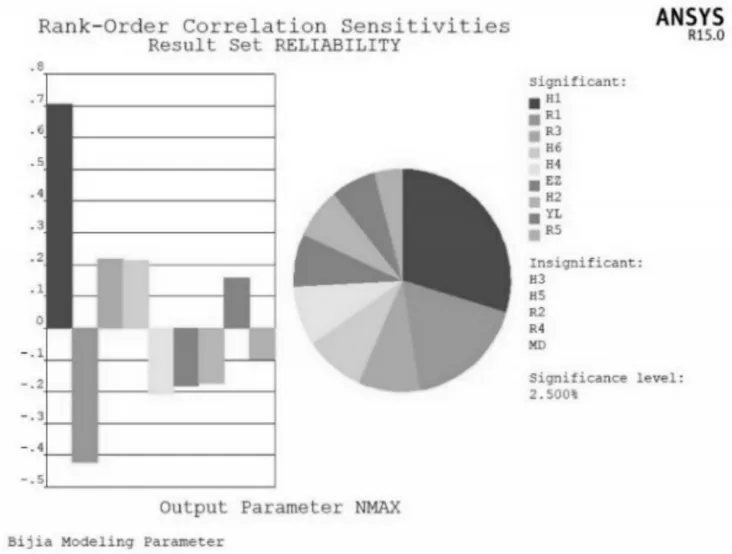
圖6 位移NMAX的靈敏度Fig.6 Sensitivity of Displacement NMAX

此外，餅圖體現了隨機輸入參數對NMAX參數的影響程度。從影響程度來看，臂架長度H1影響最大，為正向作用；臂架寬度R1影響次之，為負向作用。而這些參數如臂架液壓缸支撐點寬度H3和半徑R4、臂架與轉臺鉸接點寬度H5和半徑R2以及材料密度MD對臂架位移幾乎沒有影響，因此在分析中可以作為定值以提高分析速度。

如圖7所示，從SMAX餅圖可以看出，臂架寬度R1增大時，臂架的應力將會顯著減小，適當的增加臂架寬度可以達到降低臂架應力的目的；臂架長度H1增大時，臂架的應力將會增大，因此臂架長度不能太長。此外，臂架之間鉸接點半徑R3和寬度H6、臂架承受位置壓力YL以及臂架液壓缸支撐點寬度H3的值增大時，臂架承受的應力均會增大；臂架液壓缸支撐點半徑R4、臂架高度的一半H2以及臂架板厚度R5的值增大時，臂架承受的應力均會減小。

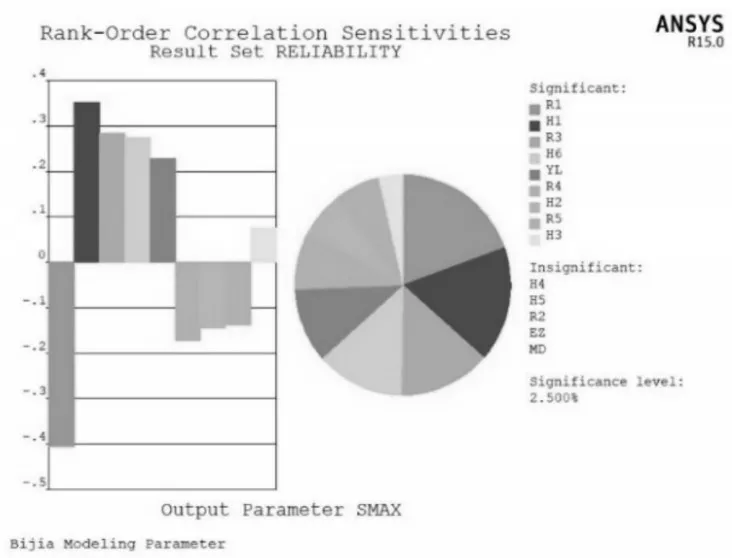
圖7 應力SMAX的靈敏度Fig.7 Sensitivity of Stress SMAX

從影響程度來看，臂架寬度R1影響最大，為負向作用；臂架長度H1影響次之，為正向作用。而臂架液壓缸支撐點與鉸接點距離H4、臂架與轉臺鉸接點寬度H5和半徑R2以及材料的彈性模量EZ和密度MD幾乎沒有影響。

6 臂架的響應面法可靠度分析

6.1 響應面法介紹

響應面法的優勢在于在保證分析精度的基礎上減少了仿真循環次數。進行響應面法分析首先要進行仿真循環計算以確定分析數據，然后進行回歸分析確定近似函數。響應面法中隨機輸入與輸出變量關系式為：

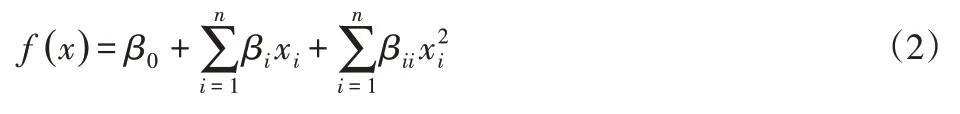
式中：n—隨機變量個數，β0—常數項，βi—線性系數，βii—二次項系數。

PDS模塊中響應面法分析主要有兩種擬合響應面的方法，分別是中心合成法（CCD抽樣）和BOX-Behnken矩陣法［10］。本文采用第一種CCD法，此方法原理公式用2N-f表示，N為隨機變量的數目。其優勢在于會隨著N變化會自動改變f的值以保證二次項系數所獲得的精度。

6.2 擬合響應面結果分析

進行分析設置后，PDS模塊會自動確定求解次數。查看抽樣曲線，如圖8為臂架長度H1以及臂架之間鉸接點半徑R3變量的抽樣過程圖。可以看出本次抽樣需要285次，且H1抽樣值在8750～9250之間波動，R3抽樣值在87.5～92.5之間波動，沒有顯著的變化，因此樣本可信度高。

圖8 部分參數抽樣曲線Fig.8 Sampling Curves of Partial Parameters

查看分析結果，并與蒙特卡羅法相比較，如表3。可以看出臂架位移NMAX的平均值是0.188m，應力SMAX的平均值是262.03MPa，兩種方法分析誤差在5%以內，符合要求。

表3 兩種分析方法的位移值與應力值比較Tab.3 The Comparison of Displacement and Stress between Two Methods

利用分析計算結果的樣本點擬合位移響應面，用RNMAX表示；擬合應力響應面，用RSMAX表示。根據蒙特卡羅法求解的靈敏度分析結果選擇影響較大的兩組關聯參數，一組是臂架長度H1與寬度的一半R1，另一組是臂架之間鉸接點寬度H6與半徑R3。分別繪制RNMAX和RSMAX的擬合響應面，如圖9～圖10所示。

對臂架位移值進行分析，如圖9（a），隨著R1參數根據正態分布隨機抽樣數值由小增大，響應面中RNMAX的位移值稍微減小；但隨著H1抽樣數值由小增大，響應面中RNMAX的位移值在逐漸增大，由圖知H1越大，RNMAX位移值越大。說明臂架寬度對位移值的影響較小，而臂架長度對位移值的影響較大。分析圖9（b），隨著H6與R3參數值由小增大，響應面中NMAX的位移值都在增大，說明臂架之間鉸接點寬度與半徑在受力時均會使臂架的位移增大。與圖9（a）相比較，可以看出臂架之間鉸接點寬度H6與半徑R3對位移值的影響小于臂架長度H1。

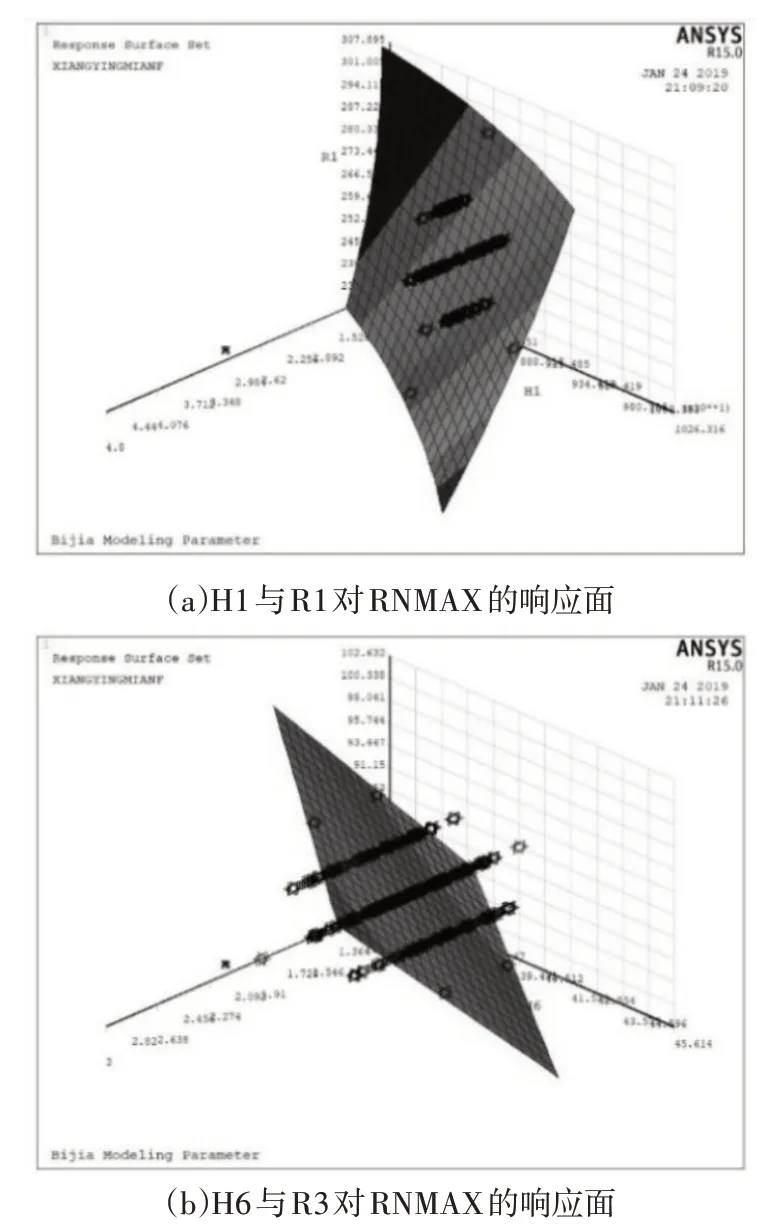
圖9 關聯參數對位移的擬合響應面分析Fig.9 Response surface analysis of displacement fitted by correlation parameters

對臂架應力值進行分析，由圖10（a）得，隨著R1參數的數值由小增大，響應面中RSMAX的應力值由大變小；但隨著H1參數的數值由小增大，響應面中SMAX的應力值經歷了由大變小在略微增大的一個過程。可以說明臂寬度對應力值的影響較大，為負向影響；而臂架長度對臂架應力值的影響小于臂架寬度，為正向影響。分析圖10（b），隨著H6與R3參數值由小增大，響應面中RSMAX的應力值都在逐漸增大。與圖10（a）對比，可以看出臂架之間鉸接點寬度H6與半徑R3對位移值的影響小于臂架寬度R1。鉸接點是臂架之間的連接位置，將后續臂架自重簡化為集中載荷施加到鉸接點，因此該位置的設計參數直接影響臂架之間的連接強度以及臂架位移應力變化情況，需要合理設計。

圖10 關聯參數對應力的擬合響應面分析Fig.10 Response Surface Analysis of Stress Fitted by Correlation Parameters

7 結論

本文以混凝土泵車臂架的第一部分為例進行了參數化建模，進行靜力分析得到了臂架的位移與應力數據，編寫了分析文件，對臂架進行了可靠度分析，得到以下結論：

（1）利用蒙特卡羅法進行可靠度分析，得到臂架位移值NMAX的平均值是0.191m，臂架應力值SMAX的平均值是273.62MPa，均在許用范圍內。在95%置信水平的條件下，位移值NMAX的可靠度為1，應力值SMAX的可靠度也為1，因此臂架結構設計可靠。

（2）進行靈敏度分析，臂架長度H1對位移值NMAX正向影響最大，臂架寬度的一半R1負向影響次之；臂架節臂寬度的一半R1對應力值SMAX負向影響最大，臂架長度H1正向影響次之；因此在后續臂架設計與改進中，需著重控制這些參數。

（3）使用響應面法分析，得到臂架位移值UMAX的平均值是0.188m，應力值SMAX的平均值是262.03MPa；并與蒙特卡羅法比較，相對誤差在5%以內。

（4）進行兩組關聯參數對臂架位移與應力的擬合響應面分析。在位移分析中臂架長度H1影響最大，為正向作用；臂架寬度R1影響次之，為負向作用；在應力分析中臂架寬度R1影響最大，為負向作用；臂架長度H1影響次之，為正向作用。