基于動力學分析的差速驅動AGV原地轉向穩定性研究

張 瑞，盧林芳，王婷婷

（鄭州大學機械工程學院，河南 鄭州450001）

1 引言

自動導引運車是一種以電池為動力，裝有電磁導引設備或光學導引設備，能夠自動沿著預定軌道行駛的自動化車輛［1］，應用于倉儲物流中，極大地提高自動化水平、降低人工成本，但其安全性與穩定性仍需做深入分析與研究［2］。某型前輪差速驅動式偏心貨叉AGV可實現在倉儲物流運輸中零半徑原地轉向，但在轉向過程中其穩定性較差，出現AGV側滑，驅動輪滑轉/滑移等現象。目前，國內外有許多針對AGV差速轉向的研究。其中，文獻［3］通過靜力學分析，研究差速轉向的可行性，并根據仿真，驗證了差速轉向的可行性。文獻［4］對AGV小車靜力學模型進行分析，驗證了一個驅動輪靜止，另一個驅動輪運動這種轉向方式的可行性。文獻［5］分析了輪式車輛速差轉向過程中輪胎工作狀態，并參考履帶車輛轉向理論，得出速差轉向輪式車輛的轉向阻力系數模型。但針對這種偏心式AGV原地轉向穩定性的理論研究較為缺乏。

針對差速驅動式AGV原地偏心轉向模型，進行動力學分析，推導AGV轉向穩定性的理論公式，獲得車體結構參數與運動參數對AGV轉向穩定性影響，并通過仿真實驗，驗證了理論推導的正確性。最后，依據理論推導以及仿真，對相關參數進行優化，改善了AGV轉向的穩定性。

2 AGV模型及參數

貨叉式前輪差速驅動偏心AGV如圖1所示，AGV前側為貨叉，后側布置電池、電機、配重塊等，車身為框架結構，兩前輪為差速驅動輪可實現原地零半徑轉向，后輪為萬向輪起支撐作用，轉向時能夠滿足阿克曼幾何學原理［6］。該AGV用于倉儲物流，水平路面運行，速度不超過1.5 m/s，屬于平面低速運動［7］。AGV通過二維碼引導直線行駛，到指定位置后前軸左右兩輪執行反方向同轉速運動，帶動AGV繞旋轉中心O（如圖2所示），實現勻加速-勻速-勻減速運動使車體轉向90°。

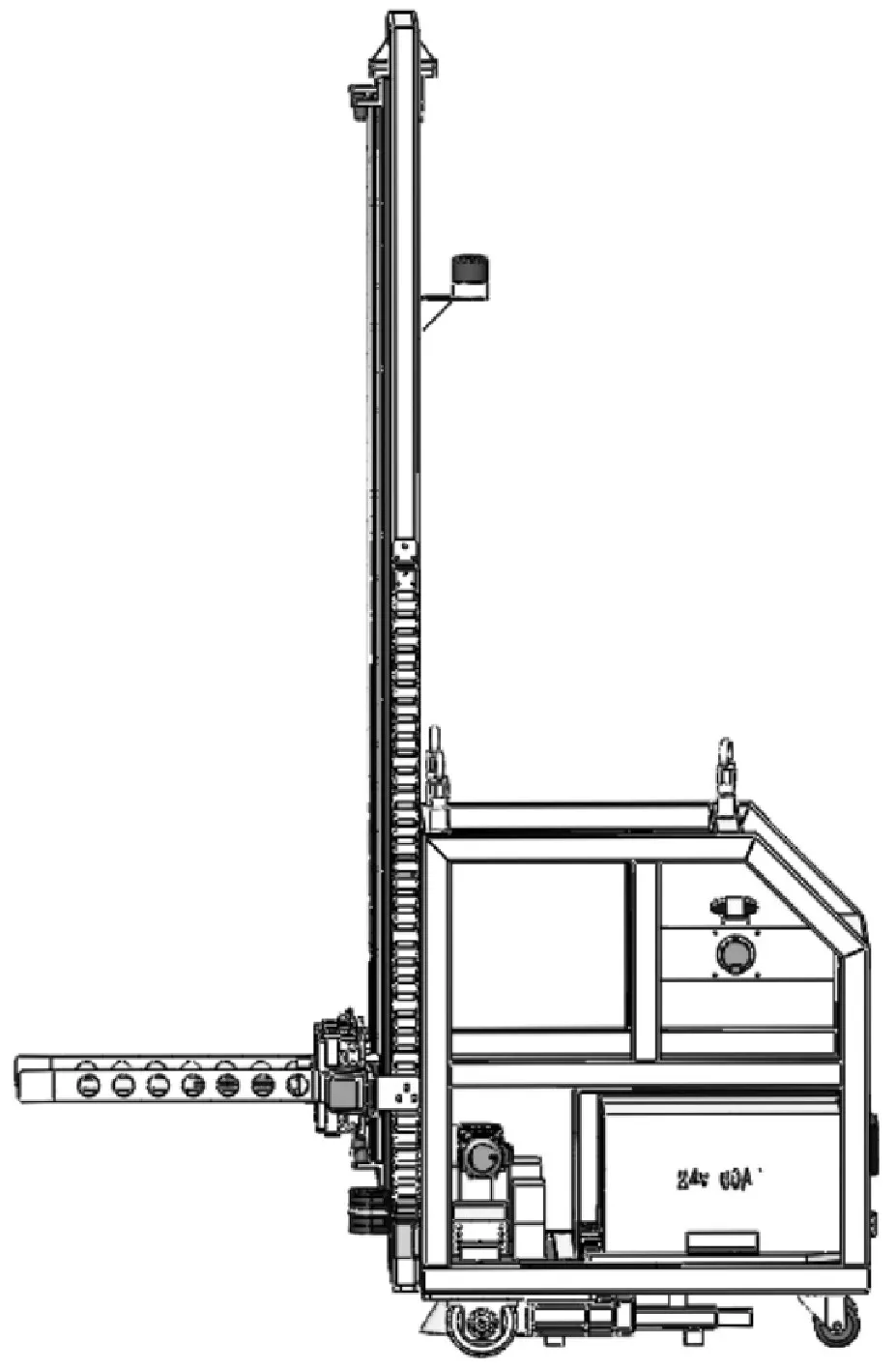
圖1 AGV實車模型Fig.1 AGV Model

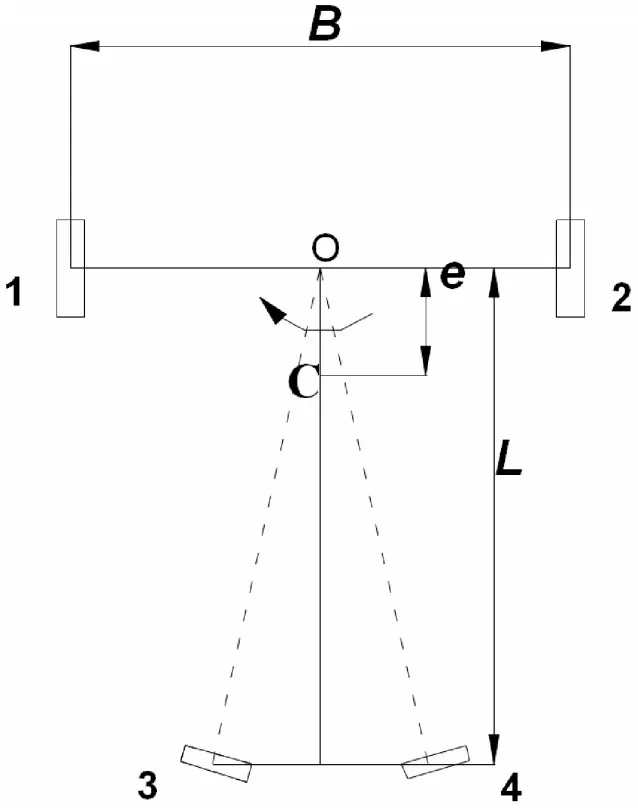
圖2 AGV簡化模型Fig.2 Structure Sketch of AGV

AGV總質量為m，兩驅動輪的輪距為B，前后軸距為L，車體質心位于C點，偏心距為e，質心高度H，驅動輪與地面之間的靜摩擦系數根據AGV運行路面及車輪材料確定為μs=0.6，滾動摩阻系數fR。

3 AGV轉向穩定性分析

針對AGV原地加速度轉向過程分析，AGV受力如圖3所示，兩驅動輪y方向上受地面對其作用力Fy1、Fy2，x方向上受靜摩擦力Fxs1、Fxs2；萬向輪上受滾動阻力FR3和FR4，分解得FxR3、FxR4、FyR3和FyR4；慣性力在x、y方向的分解，得

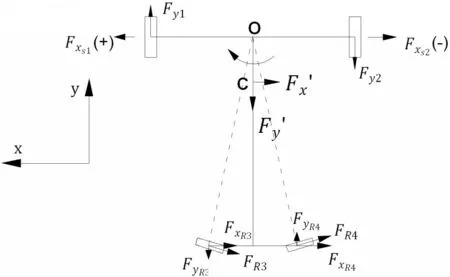
圖3 AGV受力分析Fig.3 Force Analysis of AGV

到F′x和F′y。采用動靜法［8］，列出平衡方程：

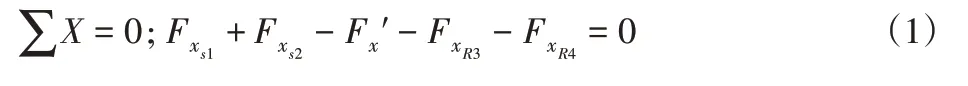
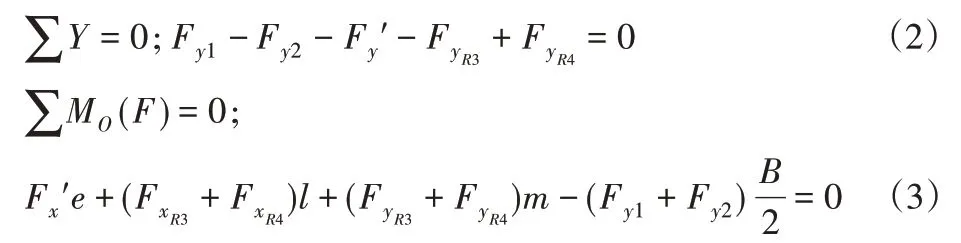
兩側驅動輪垂向載荷相等，則式（1）為：

代入公式（2）-（4）中：

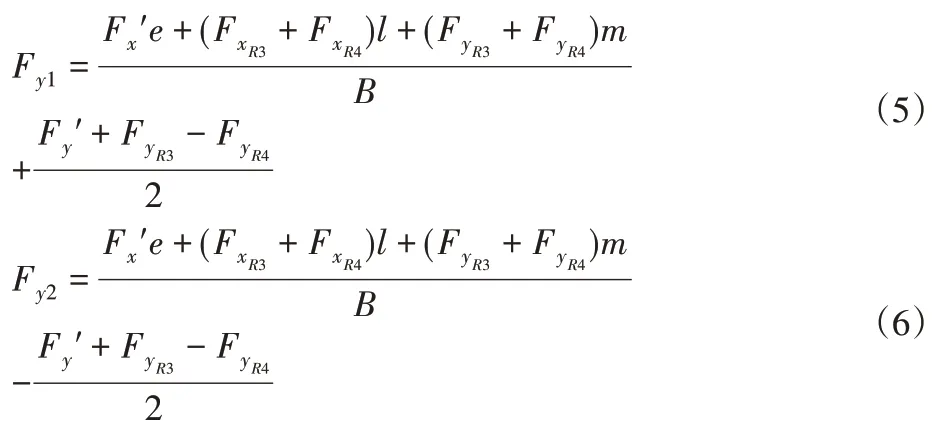
3.1 AGV出現側滑導致轉向不穩定

根據公式（1），在x方向上，當驅動輪的最大靜摩擦力合力小于AGV所受其它合力時，AGV將出現側向的滑動，為避免此發生，則：

將AGV相關尺寸、系數代入（7）中，即：

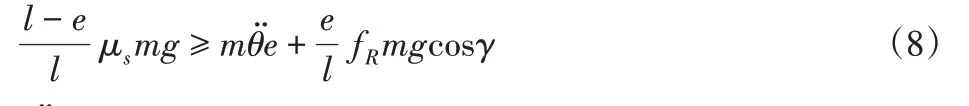
式中：—AGV在轉向過程中的角加速度，γ—萬向輪滾動阻力與其x方向上分力的夾角。

3.2 驅動輪出現滑轉/滑移導致轉向不穩定

AGV加速轉彎過程中，當地面給驅動輪提供的力形成的力矩無法達到小車圓周運動的慣性力矩時，驅動輪將出現滑轉，為避免該情況的發生：

圖2中，慣性力會對車體載荷轉移造成影響。Fx′造成左右輪子載荷轉移，Fy′造成前后輪載荷轉移。分別以右側輪、后輪與地面接觸點為支點，列力矩平衡方程：

式中：N1—輪1、3所受支持力，N1′—輪1、2所受支持力，以左側驅動輪1為對象，由公式（9）、（10）、（11）得：

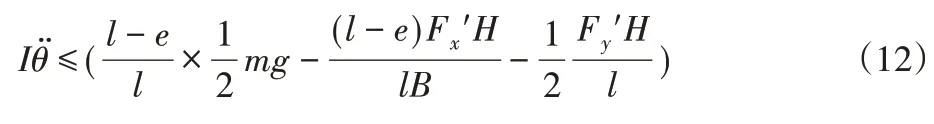
公式（12）為考慮載荷轉移后，驅動輪避免出現滑轉/滑移的條件，對比公式（9），可以看出，實際情況相對于不考慮載荷轉移時驅動輪更易發生滑轉/滑移。

3.3 兩驅動輪加速度值差異導致轉向不穩定

左側驅動輪的受力分析如圖4所示，輪半徑為r，質量為m1，車身對輪的作用力為FP，驅動力偶矩Me，地面對驅動輪的支撐力N，以及驅動輪做平面運動的慣性力FQ=m1a和慣性力偶MQC′=IC′α，AGV轉向時產生的慣性力F′y在左邊驅動輪上的分力Fy1′，Fy1′為公式（5）、（6）中的最后一項驅動輪作純滾動時：

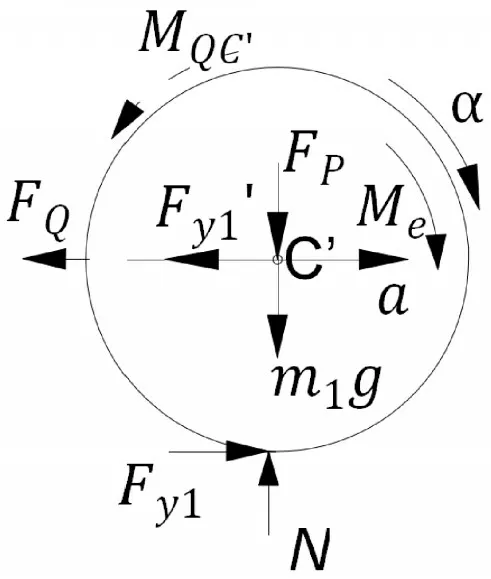
圖4 驅動輪受力Fig.4 Force Analysis of Driving Wheel

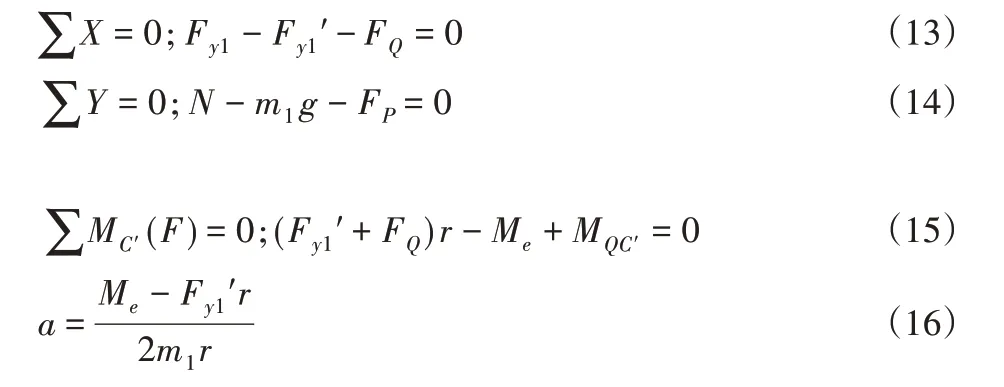
同理，對右側驅動輪進行分析，可得：

兩驅動輪輪心位移速度實時相等才能保證AGV實現零半徑的 原 地 轉 向，而 公 式（16）與 公 式（17）中，由 于Fy1′≠0導致左右驅動輪的加速度不相等，因此產生AGV轉向不穩定。

由公式（8）、（12）、（16）、（17）可知：AGV原地轉向的穩定性涉及AGV車體轉向角速度、角加速度、質心位置以及車體尺寸因素。為進一步分析各參數對AGV原地轉向穩定性的影響，后文通過仿真分別進行分析，而上述推導為后文的仿真研究提供理論依據。

4 AGV原地轉向仿真分析

通過上述理論推導，得出影響AGV原地轉向穩定性的相關參數。采用ADAMS軟件對AGV原地轉向進行仿真，分別針對所推導公式中的角速度θ˙、角加速度θ¨、偏心距e以及車體尺寸等參數進行仿真實驗，仿真模型，如圖5所示［9］。

圖5 AGV仿真模型Fig.5 AGV Simulation Model

4.1 速度對AGV轉向穩定性的影響

由于車體轉向角速度取決于驅動輪角速度，為方便設置，對AGV驅動輪不同轉速下驅動輪輪心位移速度進行仿真，得到旋轉中心的最大偏移量曲線以及驅動輪角速度為1445 deg/s的輪心位移速度曲線，如圖6～圖7所示。

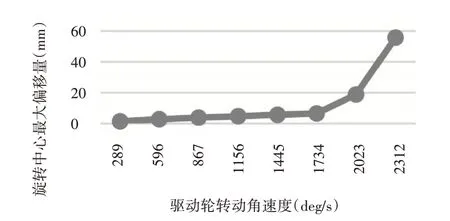
圖6 最大偏移量曲線Fig.6 Maximum Offset Curve of Rotation Center

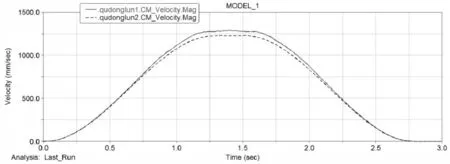
圖7 驅動輪輪心位移速度曲線Fig.7 Driving Wheel Displacement Velocity Curve

由仿真結果可知，AGV低速時，旋轉中心的最大偏移量（轉向過程中，理論上旋轉中心點位置與實際上該點的最大差值）不到1.5 mm。當速度較大時，如圖7所示，兩驅動輪加速度的差值較大，隨著速度的增大，這種差值增大，旋轉中心的偏移量變大，驗證了公式（16）、（17），隨著速度的增大，兩驅動輪的加速度值差異增大，導致旋轉中心在水平面上的偏移量增大。

4.2 加速度對AGV轉向穩定性的影響

針對不同加速度進行仿真，結果如圖8，以及在0.1 s的加速時間下驅動輪輪心位移速度曲線，如圖9所示。

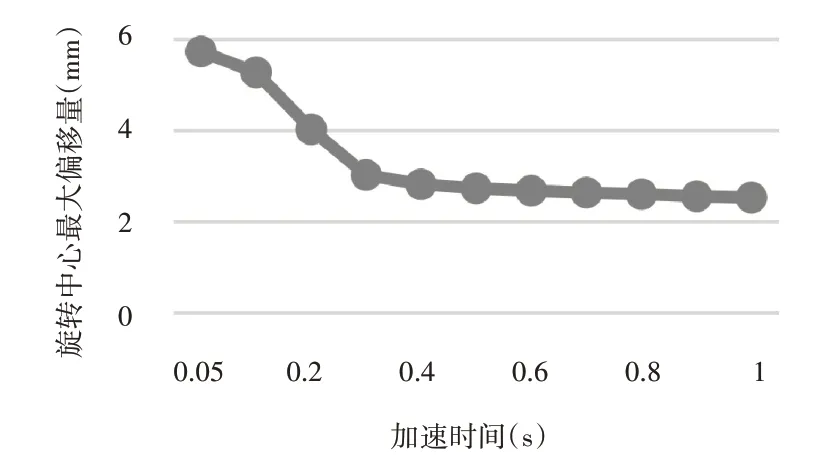
圖8 最大偏移量曲線Fig.8 Maximum Offset Curve of Rotation Center

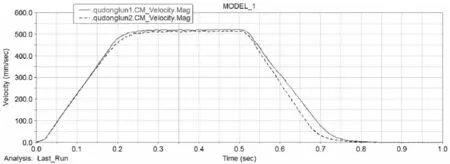
圖9 驅動輪輪心位移速度Fig.9 Driving Wheel Displacement Velocity Curve

從圖8看，加速度對兩驅動輪的速度差異影響并不大，符合之前動力學平衡方程：加速度只對AGV的x方向上的受力起影響。在加速度時間小于0.3 s，旋轉中心最大偏移量的變化明顯要大于加速時間大于0.3 s，符合公式（8）所分析：加速度達到一定時，x方向上的慣性力大于車輪的最大靜摩擦力，AGV會出現滑動；圖9中，加速時間為0.1 s，AGV在設置的停止轉動時繼續運動，驅動輪出現了明顯的運動遲滯，隨著加速度的增大，這種現象更加明顯。

4.3 質心位置對AGV轉向穩定性的影響

質心位置包括水平方向的位置，即偏心距e和質心高度H。對不同偏心距的AGV轉向進行仿真實驗，得到相應的仿真結果，以及偏心距為20 cm時驅動輪輪心位移速度曲線。

從圖10看，旋轉中心的偏移量隨偏心距的增大而增大。如圖11，偏心距較大時，兩驅動輪的速度差異相當明顯，對應的旋轉中心的偏移量也非常大。偏心距在公式（8）、（9）、（11）以及公式（12）中均有涉及，偏心距對穩定性很重要，它會使轉向過程中出現驅動輪側滑，滑轉/滑移以及驅動輪加速度不一致。

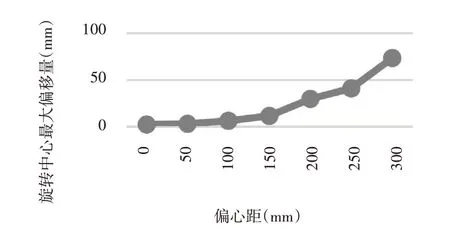
圖10 最大偏移量曲線Fig.10 Maximum Offset Curve of Rotation Center

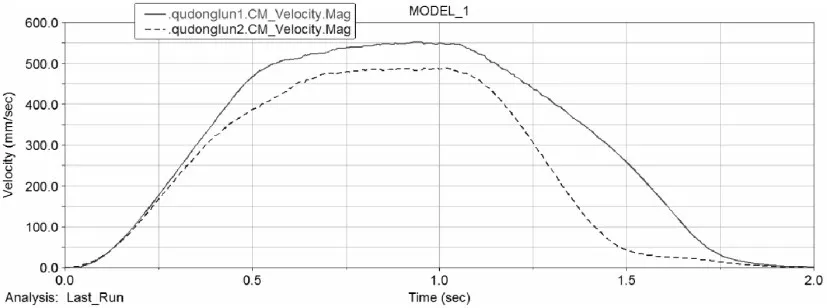
圖11 驅動輪輪心位移速度曲線Fig.11 Driving Wheel Displacement Velocity Curve

固定偏心距，對不同的質心高度進行仿真，其對穩定性的影響，如圖12所示。

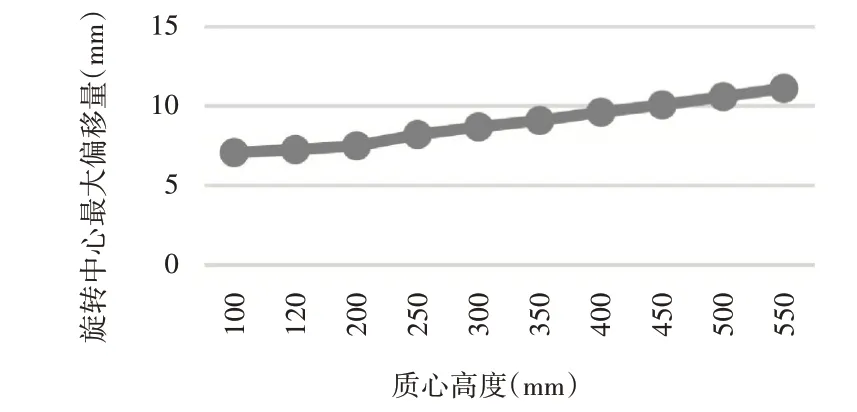
圖12 各質心高度下旋轉中心最大偏移量情況Fig.12 Maximum Offset Curve of Rotation Center in Different Centroid Height

由圖12可知：質心高度對AGV轉向穩定性影響很小，質心高度從10 cm到55 cm，其旋轉中心最大偏移量的變化范圍僅在6～12 mm之間。質心高度H對轉向時驅動輪出現滑轉/滑移現象有較小影響。

4.4 車體尺寸對AGV轉向穩定性的影響

車體尺寸包括車體長度、寬度，分別對車體長度、寬度進行仿真實驗，得到以下仿真結果。

圖14 不同長、寬車體驅動輪輪心位移速度曲線Fig.14 Displacement Velocity Curve of Driving Wheel in Different Length and Width of Vehicle Body

從圖13、14看，車體長度、寬度對AGV轉向影響較小，且長度與寬度對AGV轉向的影響在量上近乎一致，與理論分析一致。從驅動輪速度曲線來看，車體長寬不同時，兩驅動輪達最大速度時的速度差異并不大，而車體長寬偏大，運動遲滯現象更明顯，驗證了公式（9）中車體長寬的增大引起AGV轉向過程中慣性力矩過大，造成驅動輪出現滑轉/滑移。

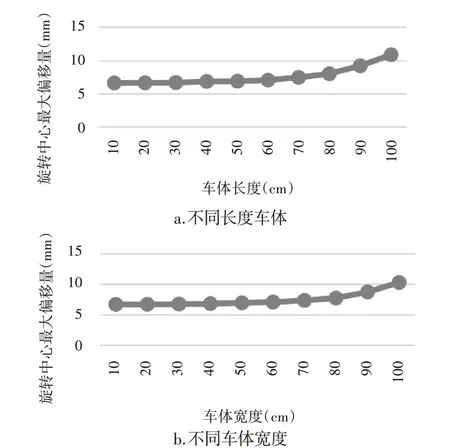
圖13 不同車體尺寸下旋轉中心偏移情況Fig.13 Maximum Offset Curve of Rotation Center inDifferent Size of Vehicle Body

5 AGV結構優化

通過上述分析與仿真可知，AGV轉向速度、加速度、偏心距以及車體尺寸對其轉向穩定性影響比較大。對這些參數進行優化，以提高AGV原地轉向穩定性。

偏心距過大導致AGV轉向出現滑轉、兩驅動輪加速度值差異過大以及驅動輪出現滑轉/滑移，而偏心距過小又會導致AGV在減速過程中出現前傾。對前輪與地面接觸為支點，列力矩平衡方程：

式中：N2′—地面對后輪的法向載荷，當N2′為0時，AGV有前傾的危險，a′—AGV直線行駛時的最大減速度，發生在AGV緊急停車時，需要在100 mm內從速度1 m/s減到0，可得a′—5m/s2。H取原設計的30cm，N2′為0時，得e=15.3cm。

對車體尺寸進行基于穩定性的輕量化設計，建立車體結構優化模型。

min：AGV車體框架體積

設計變量：框架邊長以及型材截面邊長

約束：材料許用強度

優化后的結果，如表1所示。

表1 優化前后各參數值Tab.1 Parameter Values before and after Optimization

AGV結構優化后，再次仿真，優化前后仿真結果如圖15、16所示，相同速度、加速度下，優化前兩驅動線速度一致性較差，優化后兩驅動輪線速度曲線幾乎保持一致；優化前，驅動輪加速和減速結束時都出現較為明顯的滑轉/滑移，而優化后，車體在驅動輪停止加速、減速時車體停止運動，即沒有滑轉/滑移；優化后的AGV旋轉中心偏移量大幅度減小，從最大偏移量接近12.5 mm降至僅4.6 mm。綜合分析，AGV原地轉向的穩定性在結構以及尺寸優化后得到很大的改善。

圖15 結構以及尺寸優化前的穩定性情況Fig.15 Stability of Vehicle Structure and Size before Optimization

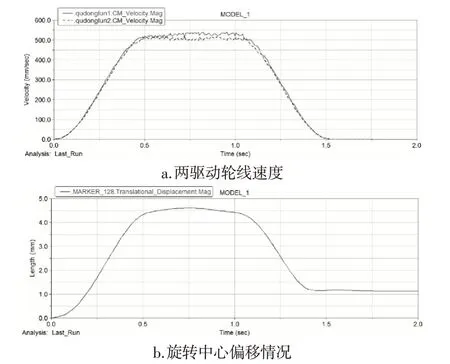
圖16 結構以及尺寸優化后的穩定性情況Fig.16 Stability of Vehicle Structure and Size after Optimization

將優化結構參數代入公式（8）、（9），為了使轉向過程時間最短，求得AGV驅動輪線加速度amax=2.34m/s2。

AGV轉向速度的增大造成轉向過程中兩驅動輪加速度差異增大，而為了快速完成轉向，AGV的速度不應過低。通過不同速度下的仿真實驗，尋求AGV能夠穩定轉向，又能以較快速度完成轉向的最優速度值。仿真結果如圖17所示，由于該AGV采用二維碼導航的方式，根據相機識別的范圍（12 cm×15 cm），以及二維碼的邊長（2 cm×2 cm），可以算出允許最大偏差距離為4.586 cm，則驅動輪角速度為1341 deg/s既符合要求，又保證最快速度轉向。

圖17 各速度下旋轉中心最大偏移Fig.17 Maximum Offset Curve of Rotation Center in Different Speed

6 結論

（1）對AGV偏心原地轉向過程進行動力學分析，獲得相應的理論公式，得出AGV結構參數與運動參數同原地轉向的穩定性的定性關系；

（2）采用ADAMS對AGV原地轉向過程進行仿真，分別針對速度、加速度、偏心距、車體尺寸等參數進行仿真實驗，通過各參數對AGV轉向穩定性的影響規律分析，驗證了理論推導的可靠性；

（3）最后，對AGV結構優化，獲得新的AGV結構參數與運動參數，結合仿真分析，AGV原地轉向的穩定性得到了改善。