分塊自適應加權改進大規模模糊聚類

田彥彥，孫 靜,2

（1.鄭州工業應用技術學院機電工程學院，河南 鄭州451100；2.吉林大學軟件學院，吉林 長春130000；）

1 引言

隨著計算機技術的發展，數據的大規模增長和信息系統的云服務化成為基礎應用，海量化、多樣化和復雜化成為數據處理的常態，如何從這些數據中提取有用信息，逐漸被人們所重視，聚類可以從各種無標記數據中通過一定的判斷策略發現數據的內在關聯而實現無監督聚類，對分析或挖掘熱點話題等信息具有重要的作用，已在計算機視覺、數據挖掘、審計評定、云計算、自動化控制以及網絡安全等學科領域具有眾多的應用，也是近幾年數據處理領域研究的重點［1］。

模糊聚類［2］基于模糊集理論分析數據集中數據對各個聚類中心的模糊隸屬度，基于模糊集理論可以實現更準確的聚類分析，多視角聚類［3］通常以傳統聚類方法為基礎，將其目標函數擴展為多視角，并對擴展后的目標函數添加約束以平衡視角一致性和聚類貢獻的差異性。為此，文獻［4］聯合視角內劃分與視角間協同的學習機制，提出多代表點一致的多視角模糊聚類算法，并通過拉格朗日乘子和KKT條件進行目標函數優化；文獻［5］基于稀疏相似和最大熵提出兩級變權的多視角自適應聚類算法；文獻［6］聯合NMF協同提高多視角聚類的相似矩陣計算，以獨立準則共享視角信息，從而優化冗余共享提高算法聚類性能。

分布式計算有效提高了大規模數據集聚類的處理效率，但其節點間的數據通訊占用了額外的資源，為解決節點通訊對資源的占用，文中提出基于大數據集抽樣分塊的多視角自適應模糊聚類算法，算法在改進多視角模糊聚類基礎上，通過數據抽樣分塊和自適應加權塊內聚類實現大規模數據集聚類。實驗結果驗證了算法的有效性。

2 模糊聚類算法的原理

設規模為N的待聚類數據集為X={x1,x2,…,xN}N×D，D為數據集中數據的維數，N?D，設V={v1,v2,…,vC}C×D為C類聚類中心，對象x（nn=1,2,…,N）劃分為第c=1,2,…,C類聚類中心的隸屬度記為為模糊劃分矩陣，則基于C均值的模糊聚類算法FCM（Fuzzy C-means）的聚類目標函數可以表示為：

使式（1）所示目標函數取得局部極小值則可以得到數據集的模糊劃分矩陣U=[ui,j]，其迭代優化計算式分別為：

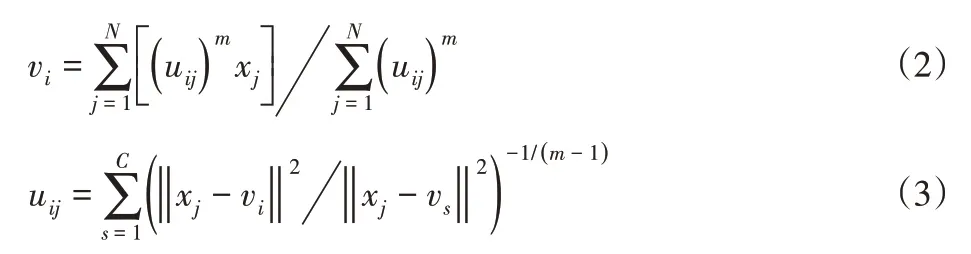
式中：m—模糊指數，針對經典FCM算法的unc無法精確表達數據集的分類信息問題，文獻將中立與拒分兩種度量策略引入到FCM算法中，改進后的正則化模型［7］，可描述為

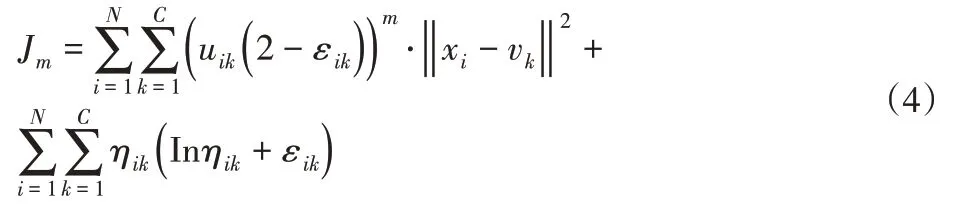
式中：η=[ηij]、ε=[εij]—聚類算法的模糊中立度矩陣與模糊拒分度矩陣，其相應的約束條件為∑uij( 2-εik)=1和∑(ηij+εik/c)=1，采用拉格朗日乘子法可以根據式（4）計算相關參數。為提高式（4）改進模型的魯棒性，將文獻［10］中的鄰域正則約束引入式（4），提出具有抗噪優化的魯棒模糊聚類方法，其改進后的目標函數為：

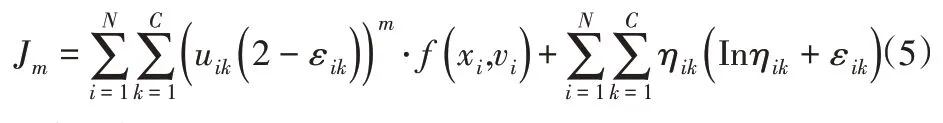
式中：f(xi,vi)—描述了領域空間信息約束特征，主要用于提高算法的魯棒性并抵制背景噪聲影響，其計算式為：

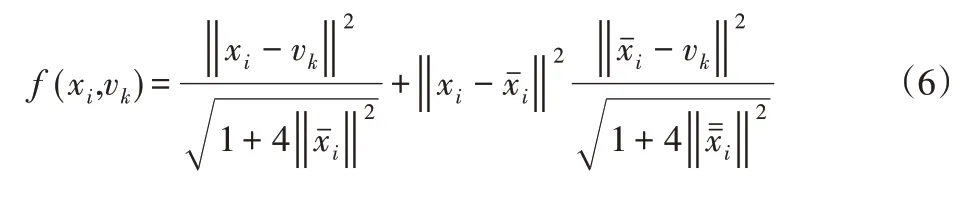
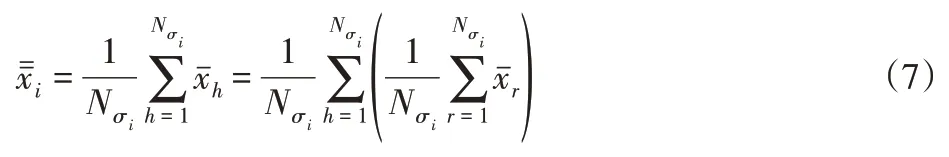
為提高聚類算法對多樣化數據的適應性，通過低秩約束和熵加權對改進后的自適應魯棒模糊聚類算法進行多視角擴展，通過視角系數優化算法在迭代過程中對可分離性視角的權重分配，從而提高算法對多樣化數據的聚類性能，低秩約束有利于改進算法在聚類過程中的多視角一致性，而熵加權則有利于保持不同視角數據之間的聚類貢獻差異性。

高頻接觸振動產生巨大的垂直力增量，使鋼軌塑變層遭受反復和快速的錘擊作用，逐漸在鋼軌表面形成明暗相間的波浪形磨耗。當有切向力作用的動輪經過其上時，瞬間的局部接觸間斷可使動輪積聚起很大的能量，一旦在波浪形的峰部恢復接觸時，聚合的能量就驟然被釋放出來。

令多視角數據的各視角系數為wk≥0，則有，則擴展算法的熵加權正則項為：

而低秩約束可以將多視角約束為核范數最小化求解問題，即Γ(U)=‖U‖，U－多視角隸屬度組成的矩陣，這樣基于低迭約束和熵加權的改進算法的目標函數可以表示為：

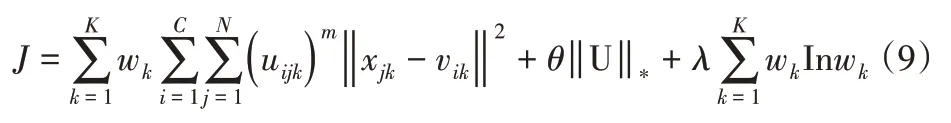
式中：N—數據量，C—聚類中心數，θ、λ—正則化因子。對于式（9）的迭代求解，通過固定其中的w和U，同時迭代更新聚類中心矩陣V，可得第t+1次迭代計算得到的聚類中心的解為：

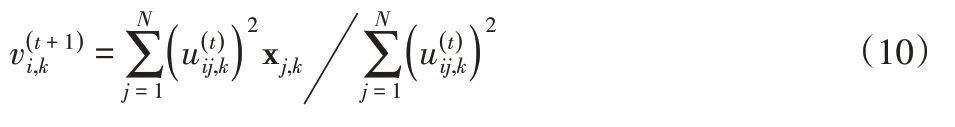
而通過固定式（9）中的w和Z，同時迭代更新模糊隸屬度，可得第t+1次迭代計算得到的模糊隸屬度U(t)+1為：

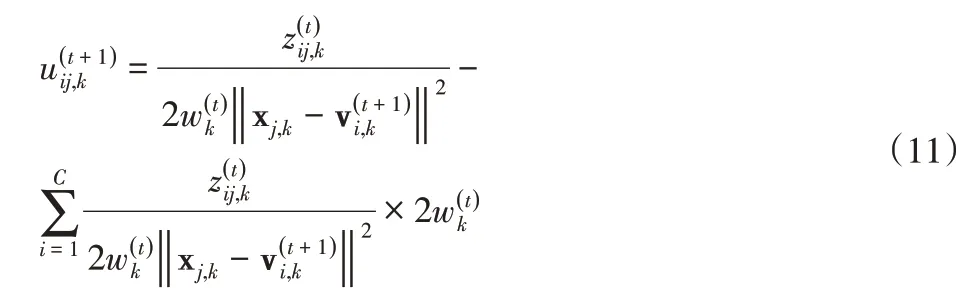
式（9）所示改進模型以等價關系融合了多視角聚類與模糊聚類的優勢，具有全局最優解［9］，但算法巨大的計算量使其在應用于大規模數據聚類時無法獲得最優聚類甚至無法得到聚類結果，為此，借鑒已有的大規模數據分塊思想，對提出的多視角自適應模糊聚類算法進行改進，以適于越來越普遍的大數據處理場景。

3 分塊加權大規模模糊聚類

大規模數據集難以一次性全部讀入內存中，因而給聚類算法的數據讀取帶來壓力，Canopy算法根據一定的數據預處理規則可以將原始大規模數據集劃分為多個數據片，每個數據包含一定數量的數據，因此可以通過Canopy算法先對數據進行分塊預處理，將原始大規模數據集劃分為可同讀入內存進行處理的小規模數據片，同時Canopy算法可以根據數據特征初步獲得數據的粗糙聚類中心，從而進一步減少后續數據處理過程的迭代次數，提高算法收斂效率。

對于原始數據集list=X={x1,x2,…,xN}N×D，預設兩個閾值T1和T2，T1＞T2，則判斷任意一個數據點P與list中剩余數據的距離值d，并將T1＜d＜T1的原始數據點作為候選的初始聚類中心，重復執行，直接所有數據被判斷一遍，同時將d＜T1的數據合并為一個臨時數據片。

在獲得初始聚類中心及其相應聚類后，對每個聚類中的數據進行隨機抽樣，并將一次抽樣結果作為一個數據分塊，根據數據規模判斷分塊數及每個數據塊的規模，并對數據塊進行編號。然后對第一個數據塊執行第2節所示的多視角自適應模型聚類算法，獲得第一個數據塊的聚類結果及其聚類的質心，由于每個聚類的質心最具有該類的代表性，因而將該質心作為代表點合并到第二個數據塊中，并參與第二個數據塊的聚類，依次類推，直接所有數據塊均完成多視角自適應模糊聚類，從而獲得最終大規模數據集模糊聚類結果。

由于從第二個數據塊開始，其中的數據除了原始抽樣數據外，還新加入了上一數據塊的代表點數據，從數據對最終聚類結果的貢獻看，由上一數據塊傳遞來的代表點對于當前塊最終的聚類具有更大的貢獻，因而從第二個數據塊開始，需要對原始抽樣數據和代表點數據賦值不同的權重，以描述其對最終聚類結果的貢獻，且隨著數據塊序號的增加，其新加入的代表點應自適應的賦值相應更大的權重，為此，文中對含有代表點的數據塊的聚類，其目標函數中增加數據的自適應權重，修改后的目標函數為：

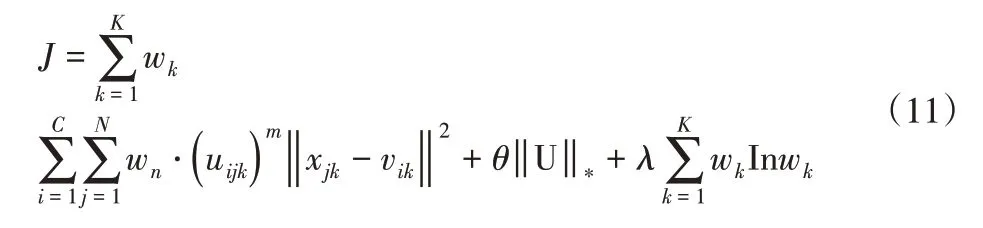
式中：wn＞0—數據權重，其描述了數據塊不同屬性數據的聚類貢獻，對于不同序號的數據塊，該權重值由前一數據塊的權重值累積得到，即

表1 大規模分塊多視角自適應FCM算法Tab.1 Large-Scale Split Field Multiview FCM Algorithm

4 實驗與分析

為驗證文中提出的分塊多視角自適應模糊聚類算法（簡記為pmvaFCM）的有效性，采用來自UCI機器學習庫的Iris和Wine數據集［10］作為測試數據，以傳統FCM算法［4］、多視角FCM算法（mvFCM）［9］作為比較算法，實驗平臺為：Intel i7 7700HQ@2.8G Hz，16G內存，NVIDIA GTX1060 6G顯存，以matlab 2016a軟件開發實驗算法。

從兩個數據集中隨機選取105條記錄進行實驗測試，數據集中加入噪聲，以多次實驗結果的聚類準確度平均值作為聚類性能評價指標，首先測試不同算法的聚類性能效率實驗結果，如表2所示和圖1所示。

表2 不同算法的聚類性能比較Tab.2 Performance Comparison of Different Algorithms

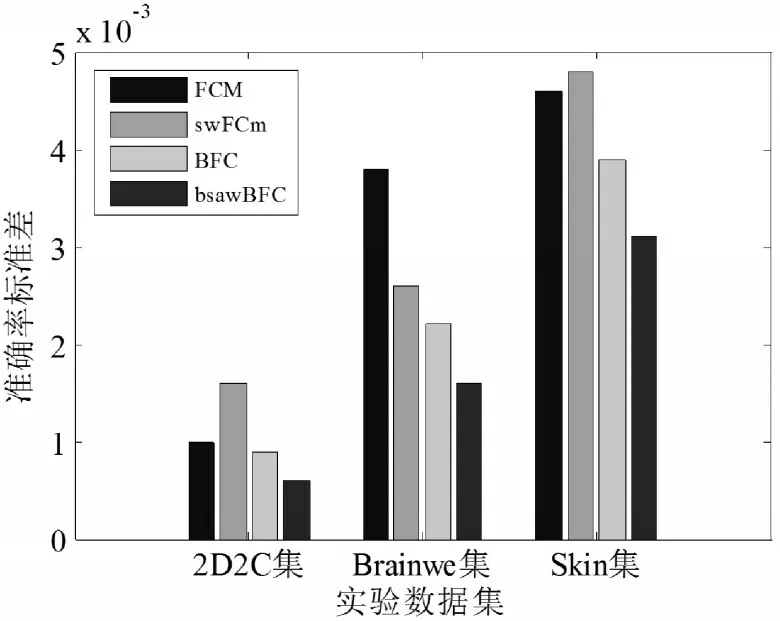
圖1 各算法聚類準確率標準差Fig.1 Standard Deviation of Clustering Accuracy of Each Algorithm

從表2和表1實驗結果可以看出，文中改進pmvaFCM算法的收斂迭代次數有了大幅減少，從而在相同硬件條件下有效減少算法的聚類時間，這主要是因為算法在將數據集分塊后，大多數數據塊僅有若干代表點等數據是的變量動，因而各數據塊的聚類迭代時間變化不大，而通過合理設置數據分塊大小，可以有效減少每個數據塊的聚類迭代次數。另一方面，從平均聚類準確率實驗結果可以看出，文中算法取得與mvFCM相似但略好的聚類準確率，這主要是因為，通過Canopy算法進行初始聚類中心提取后，后續的數據抽樣分塊及聚類初始聚類中心設置，都有了一個較為準確的參考，使得相關參數的設置更加合理，從而使得算法取得更優的識別準確率。從圖1準確度標準差可以看出，文中算法在2個數據集中均取得最小的標準差，說明文中算法具有最優的聚類穩定性。

5 結論

為解決傳統FCM模糊聚類算法在處理大規模數據集時遇到的時間復雜和內存不足等瓶頸，提出基于大數據集抽樣分塊的多視角自適應模糊聚類算法，算法通過鄰域正則約束提高傳統FDM算法的抗噪性，通過低秩與熵加權約束提高多視角一致性，以提高算法對多樣化數據聚類的適應性，最后通過Canopy算法初始聚類中心提取和數據抽樣分塊優化算法對大規模數據聚類的適應性，實驗結果驗證算法的有效性。