程序類競賽中的動態規劃算法探討

盧揚城，毛玉萃，關澤群

摘要：動態規劃問題在各類程序設計競賽中常常出現。該文首先簡單介紹了動態規劃算法，闡述了利用動態規劃解決實際問題的流程，并通過實例進一步探討了線性動態規劃、區間動態規劃、樹形動態規劃、背包動態規劃以及狀態壓縮動態規劃算法問題，簡單介紹了動態規劃算法思想在其他經典算法中的應用，最后進行了簡單總結。

關鍵詞：動態規劃;程序類競賽;實例;

中圖分類號：TP311.52? ? ? 文獻標識碼：A

文章編號：1009-3044（2021）21-0093-04

開放科學（資源服務）標識碼（OSID）：

1 動態規劃算法的概述[1-2]

動態規劃算法在是許多算法的理論基礎，在傳統決策性問題、圖論問題、字符串問題等問題中都有涉及，因此是程序設計類競賽考察的重點。

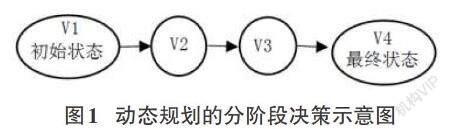
動態規劃算法的核心是利用記憶化處理方式、依托貪心思想、記錄歷史數據來達到優化時間復雜度的目的，簡而言之就是“用空間換時間”;在求解過程中采用分治思想，對問題分階段進行決策。圖1所示為動態規劃的分階段決策。

動態規劃算法需要滿足以下幾個特征：

1.1 無后效性

無后效性是指當前狀態一旦確定，則之后的所有狀態與之前的情況無關，僅僅與當前狀態的決策有關，因此要著重研究當前狀態。

1.2 最優子結構

動態規劃算法經常解決的是最值性問題。最優化子結構保證各階段求解的方案決策具有類似的最值結構，即決策滿足貪心思想下的解也一定是子解的最優解。

1.3 子問題重疊

即所分解得到的子問題之間不是相互獨立的，在之后的階段還可能被多次使用到。這一點不是動態規劃算法適用的必要條件，但是如果沒有這個特征，動態規劃算法便不具有時間上的優勢。

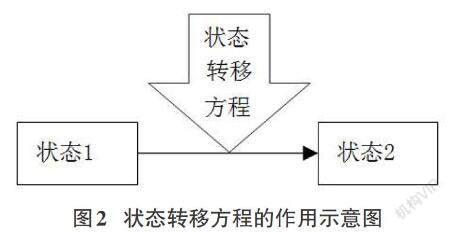
動態規劃算法中狀態定義和狀態轉移方程設計是核心。狀態定義是解決動態規劃問題的關鍵，把問題分成幾個不同的情況對這些情況的抽象描述即是狀態定義。狀態轉移方程是決策問題中的指南針，設計正確的狀態轉移方程是求解問題的重中之重，圖2表示狀態轉移方程的作用。各階段狀態由歷史狀態轉移而來，從眾多的歷史狀態中選擇哪一個就是狀態轉移方程要解決的任務。

2 動態規劃求解問題的流程[1-4]

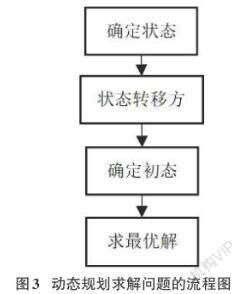
動態規劃算法由其分階段性和依托性，可將其分為正向遞推和反向遞推，利用分治思想從小問題逐漸遞推到大問題，注意遞推過程的邏輯性，觀察不同狀態間的特征及其之間的內在邏輯、不同點和相同點來得出初步遞推公式。正向遞推通常從“當前狀態可以得到哪些狀態”的大致思路思考，反向遞推通常由“當前狀態可以由哪些狀態得到”的大致思路來思考。捋順遞推過程是解決動態規劃問題十分關鍵的一步，確定了遞推關系才能解決整個問題，遞推關系的體現就是狀態轉移方程。動態規劃求解問題的過程如圖3所示。

首先確定狀態就是根據問題描述中的信息整理出相關的量，這些量必須是相互獨立的，也就是說在邏輯上問題的狀態由這些量構成，缺少任意一個量狀態問題的表示就不明確，在確定狀態量時必須兼顧內存空間的要求，不能一味地追求細致刻畫狀態，而造成冗余狀態的表示和無用信息的附加，這在動態規劃算法優化部分著重介紹;其次確定基本量、依托量。基本量通常以題干給定的信息為主，在不需要推導的情況下就可以得到。依托量通常是抽象量，指的是我們對答案的構成描述，依托量的某個狀態的全集就是最終的答案。再次根據問題描述中給定信息尋找不同量之間的遞推關系，可以運用正向遞推的方式也可以運用反向遞推的方式，通常情況下較難的題涉及的遞推思想常常與反向遞推有關，確定了遞推公式，接下來可以描述出狀態轉移方程的大致輪廓。許多涉及數組間遞推的動態規劃問題中，常見到以數組下標為基本量，以原數組數值為依托量來確定其遞推關系。描述了狀態轉移方程之后要確定狀態的初始情況，即確定初態，初態必須合乎狀態轉移方程的邏輯要求，初態的確定對算法來說有著舉足輕重的作用。最后要確定哪些狀態集合包含答案，通過遍歷該集合得到答案。

3 各類動態規劃的解題思路和應用舉例

動態規劃問題按其狀態轉移方程的形態和存儲方式，可以劃分為線性動態規劃、區間動態規劃問題、樹形動態規劃問題、背包動態規劃問題和狀態壓縮動態規劃[1，3-5]。

3.1 線性動態規劃

線性動態規劃包含了動態規劃的最基本的思想，是在線性結構上進行狀態轉移的，是最簡單的動態規劃，該類動態規劃空間復雜度一般為O（n），問題大多較為簡單。其他復雜類型的動態規劃都是在它的基礎上增加優化算法、增加狀態維度和在各種抽象數據結構上等的模型。

例1（原題見參考文獻[6]）問題簡述：一個游戲由一個棋盤和一些棋子組成，所有的棋子都用一個正整數或“開始”或“結束”來標記。玩家從起點開始，最后必須跳到終點。在跳躍過程中，玩家將訪問路徑中的棋子，但每個人必須從一個棋子跳到另一個絕對大的棋子（假設起點是最小值，終點是最大值）。所有玩家都不能倒退。一跳可以從一個棋子跳到下一個棋子，也可以跨越多個棋子，甚至可以從起點直達終點。一個球員是贏家，當且僅當他能得到一個更大的分數，根據他的跳躍解決方案。一個玩家的分數來自他跳躍路徑中棋子上的值的總和，求最大分數是多少。

這題是一道最長上升子序列的模板題。

子序列與子數組是區別。子序列指的是由原序列刪除若干元素后，剩下的元素由相對位置不變的方式得到的一個有序集合。子數組是原序列上一段連續的有序集合。

此問題可以說是動態規劃入門的經典問題并且是一個線性動態規劃。假設數組為sl，設到sl[i]的最長長上升子序列的長度為dp[i]，最初dp[i]=1，即到sl[i] 的最長上升子序列的長度初始值1，即數組中的每一個數都是包含自身的一個數的最長上升子序列 。考慮狀態轉移方程的確定，在計算dp[i]的值之前，就已經計算出sl[i]前面的最長上升子序列的長度。當數sl[i]大于往前遍歷到的數sl[j]時（j