材料性能分散性對輪盤破裂轉速預測結果的影響研究

蘇俊卿，李林駿

(中國航發四川燃氣渦輪研究院，四川綿陽 621000)

1 引言

輪盤是航空發動機的斷裂關鍵件，一旦破裂，會導致災難性后果[1]。為保證航空發動機的安全性，國內外航空發動機規范和適航標準均對輪盤的強度設計提出了嚴格的要求，明確規定了輪盤的破裂轉速儲備設計要求[2-3]。如美國發動機結構完整性大綱軍用標準[2]規定，輪盤的最低破裂轉速不得低于最大允許穩態轉速的122%。

根據規范要求，航空發動機結構設計時需要對輪盤構型進行設計優化，以保證其具有足夠的破裂轉速儲備。國內外學者提出和發展了多種輪盤破裂轉速預測方法[4-15]，如平均應力法、局部應變法、小變形解析法、大變形解析法等。在眾多方法中，基于殘余變形或塑性失穩準則的大變形有限元分析方法，主要利用輪盤材料的彈塑性本構模型來預測破裂轉速，不需要通過實際輪盤破裂試驗來修正方法本身，方便用于方案階段的輪盤設計和優化。然而輪盤材料性能具有分散性，使用該方法進行破裂轉速預測時，有必要了解和掌握材料性能分散性對其結果的影響規律。

本文針對GH4169輪盤，根據其拉伸性能數據，采用基于塑性失穩準則和大變形有限元分析方法，分別通過雙線性、多線性和非線性三種輪盤材料本構模型來描述輪盤材料變形行為，分析材料性能分散性對輪盤破裂轉速計算結果的影響。

2 基于雙線性本構模型的輪盤破裂轉速分析

利用雙線性本構模型描述GH4169合金材料的彈塑性行為，通過大變形有限元分析方法計算GH4169 輪盤的破裂轉速。考慮到所模擬輪盤材料性能及工作載荷的對稱性，僅建立整體輪盤的1/12扇形有限元模型(圖1)，設定循環對稱邊界條件，實現對整體輪盤的計算分析。

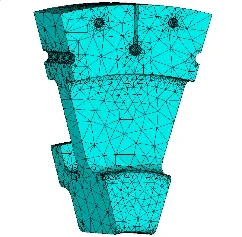
圖1 輪盤模型Fig.1 Model of disc

雙線性本構模型采用兩段線性方程來描述材料的響應曲線，對真應力-真應變曲線擬合度低，計算量小。表達式如下：

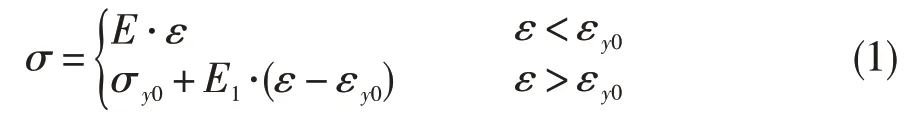
式中：σ為應力，E為彈性模量，ε為應變，σy0為初始屈服應力，εy0為初始屈服應力下的應變，E1為切線模量。對于雙線性本構模型，彈性模量、泊松比、屈服應力、切線模量是決定材料性能的主要參數。

通過試驗測得GH4169 合金試樣的彈性模量、泊松比、屈服應力、切線模量，將平均值作為基準值，設定系數k為基準值的倍數，以表示各性能參數分散性的取值范圍。在研究其中某一性能參數的分散性對破裂轉速計算結果的影響時，均假設其他參數取基準值。表1～表4 分別給出了彈性模量、泊松比、屈服應力、切線模量在典型分散范圍內基準值上下變化時，輪盤破裂轉速預測結果及其與取基準值時預測結果的偏差。

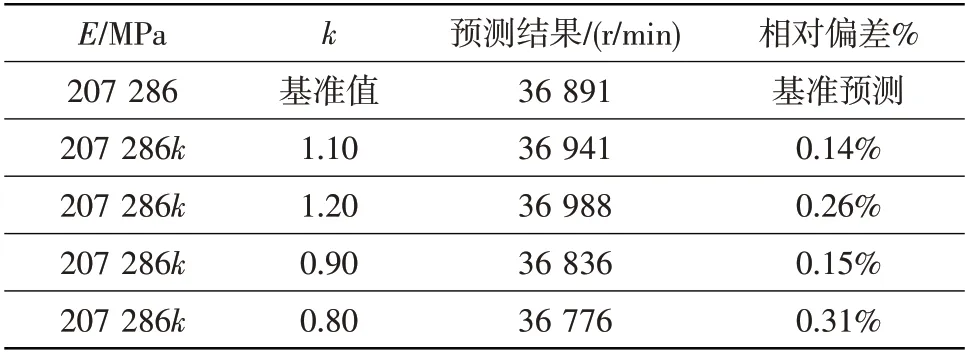
表1 彈性模量分散性對輪盤破裂轉速預測結果的影響Table 1 Contrast of prediction results of disc burst speed under different elastic modulus

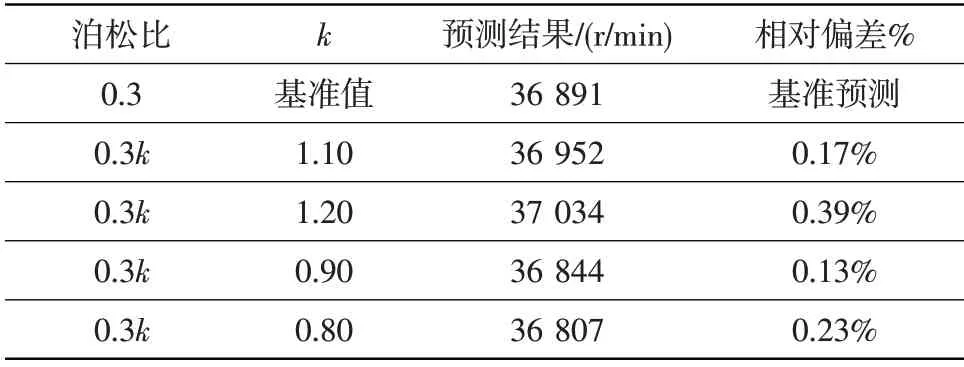
表2 泊松比分散性對輪盤破裂轉速預測結果的影響Table 2 Contrast of prediction results of disc burst speed under different Poisson ratio

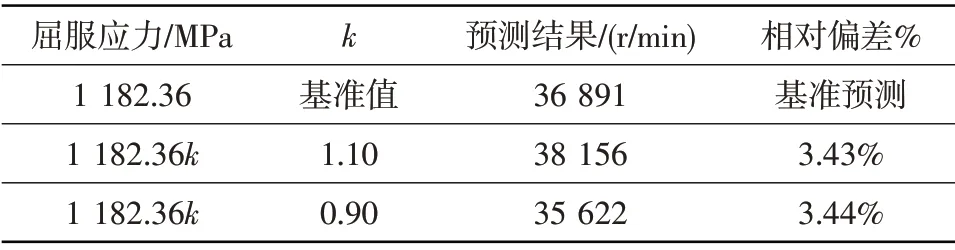
表3 屈服應力分散性對輪盤破裂轉速預測結果的影響Table 3 Contrast of prediction results of disc burst speed under different yield stress

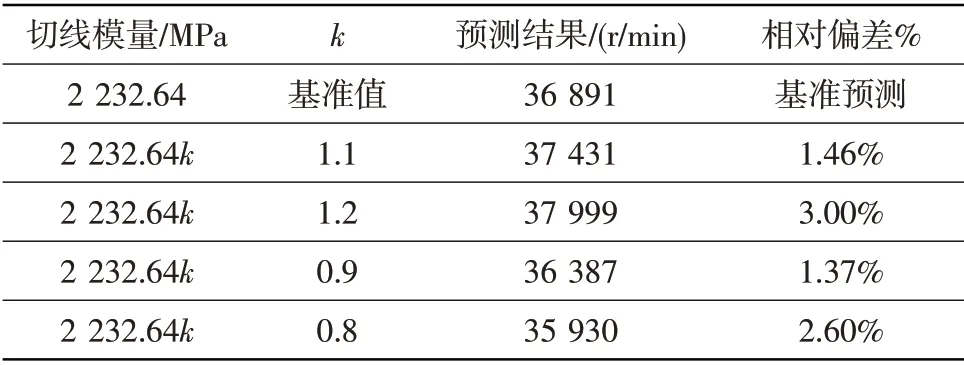
表4 切線模量分散性對輪盤破裂轉速預測結果的影響Table 4 Contrast of prediction results of disc burst speed under different tangent modulus

從表1和表2對比結果可以看出，彈性模量和泊松比在基準值上下20%范圍內變化時，破裂轉速預測結果偏差小于0.50%，影響較小。從表3和表4結果可以看出，屈服應力和切向模量分散性對破裂轉速預測結果的影響相對較大。屈服應力在基準值上下10%范圍內變化時，破裂轉速預測結果偏差在4.00%以內。切線模量在基準值上下20%范圍內變化時，破裂轉速預測結果偏差在3.00%以內。因此，當輪盤材料性能參數在典型分散范圍內變化時，基于雙線性本構模型預測的輪盤破裂轉速偏差較小，材料性能分散性對預測結果的影響較小。

3 基于多線性本構模型的輪盤破裂轉速分析

輪盤有限元計算模型同圖1。多線性本構模型是將試驗測得的材料真應力-真應變曲線采用多條直線段來描述，對真應力-真應變曲線擬合度較高，計算量適中。多線性本構模型表達式如下：

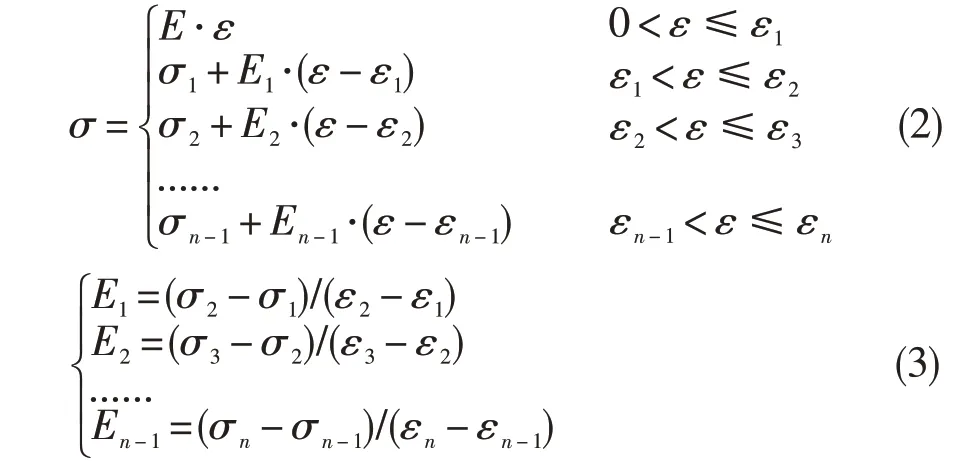
式中：(σ1,ε1)、(σ2,ε2)……(σn,εn)為多線性材料模型各分段的端點，E1、E2……En-1為各分段斜率。

試驗測試獲得10 條典型GH4169 光滑圓棒試樣拉伸真應力-真應變曲線，其拉伸性能分布在典型分散范圍內。采用10 個多線性本構模型來描述，拉伸強度從小到大依次排列，分別為多線性1至多線性10，最大拉伸強度與最小拉伸強度相差約100 MPa，如圖2 所示。基于10 種多線性本構模型預測輪盤破裂轉速，選擇拉伸強度最低的多線性本構模型1 的預測結果作為基準，其他本構模型的預測結果與其對照，見表5。

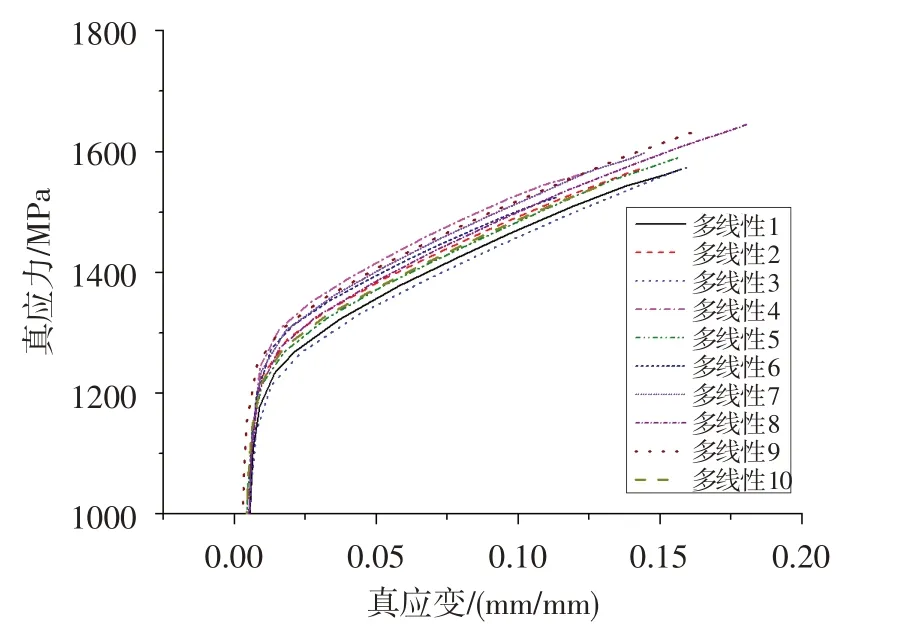
圖2 各多線性本構模型真應力-真應變曲線Fig.2 True stress-true strain curves of various multi linear models

綜合圖2和表5可看出，拉伸強度越大輪盤破裂轉速預測值越大；不同拉伸強度下材料真應力-真應變擬合曲線不同，存在分散性，由材料分散性影響的破裂轉速的預測結果相對偏差在3.00%以內。據此，當輪盤材料拉伸性能曲線在典型分散范圍內變化時，基于多線性本構模型預測的輪盤破裂轉速偏差較小，材料性能分散性對預測結果影響較小。

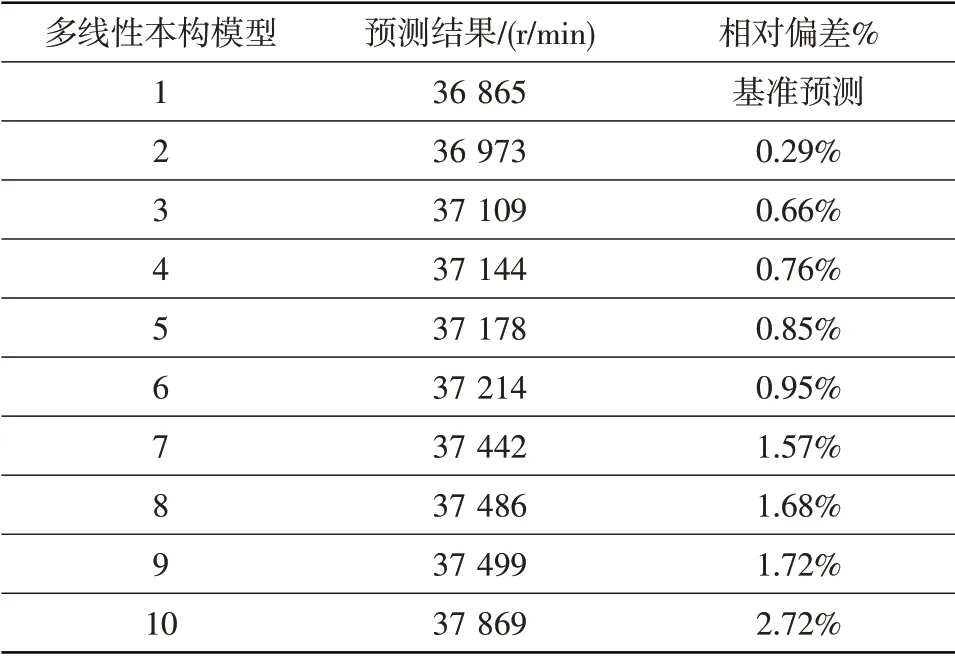
表5 各多線性本構模型的輪盤破裂轉速預測結果及對照Table 5 Prediction results of disc burst speed based on various multi linear models

4 基于非線性本構模型的輪盤破裂轉速分析

輪盤有限元計算模型同圖1。非線性本構模型對材料的真應力-真應變曲線的擬合度最高，但計算量大。典型的非線性本構模型是采用公式(4)來描述材料拉伸真應力-真應變曲線的塑性變形。

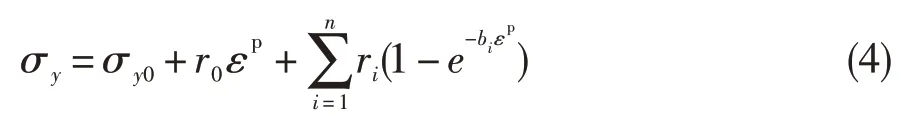
式中：σy為材料塑性流動應力；εp為塑性應變；r0、ri、bi為非線性本構模型參數；為能夠較好地描述材料塑性變形曲線同時考慮計算量，本文n取4。

基于前述10條典型的GH4169光滑圓棒試樣拉伸真應力-真應變曲線，采用非線性本構模型來描述，拉伸強度從小到大依次排列，分別為非線性1至非線性10(圖3)。基于10種非線性本構模型預測的輪盤破裂轉速見表6，仍選擇拉伸強度最低的非線性本構模型1的預測結果作為基準。

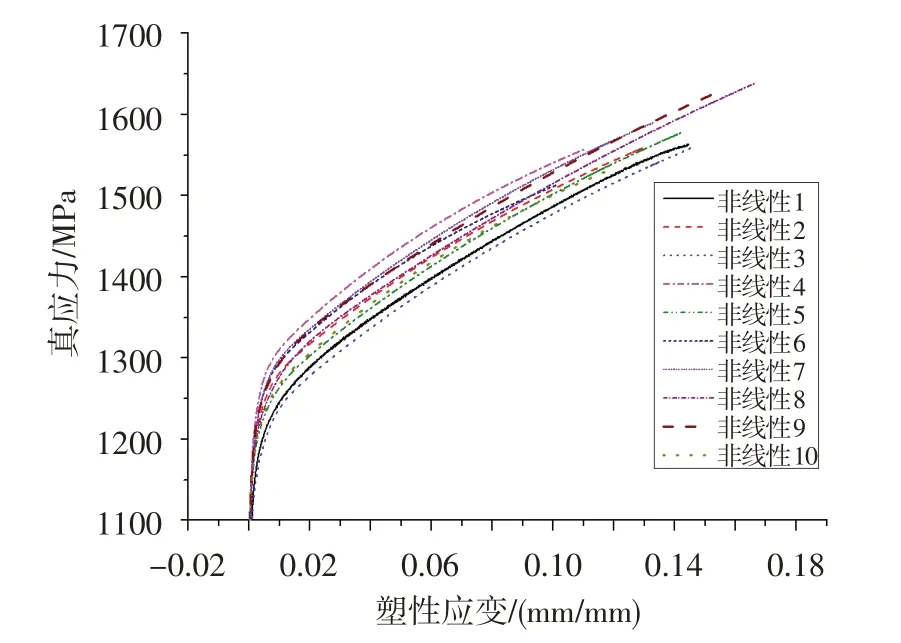
圖3 各非線性材料模型真應力-真應變曲線Fig.3 True stress-true strain curves of various non-linear models

從表6 中可看出，與多線性本構模型預測結果相似，拉伸強度越大，采用非線性本構模型預測的輪盤破裂轉速也越大。相對于拉伸強度最小的非線性本構模型1 的預測結果，相對偏差均在3.00%以內。據此，當輪盤材料拉伸性能曲線在典型分散范圍內變化時，基于非線性本構模型預測的輪盤破裂轉速偏差較小，材料性能分散性對預測結果影響較小。

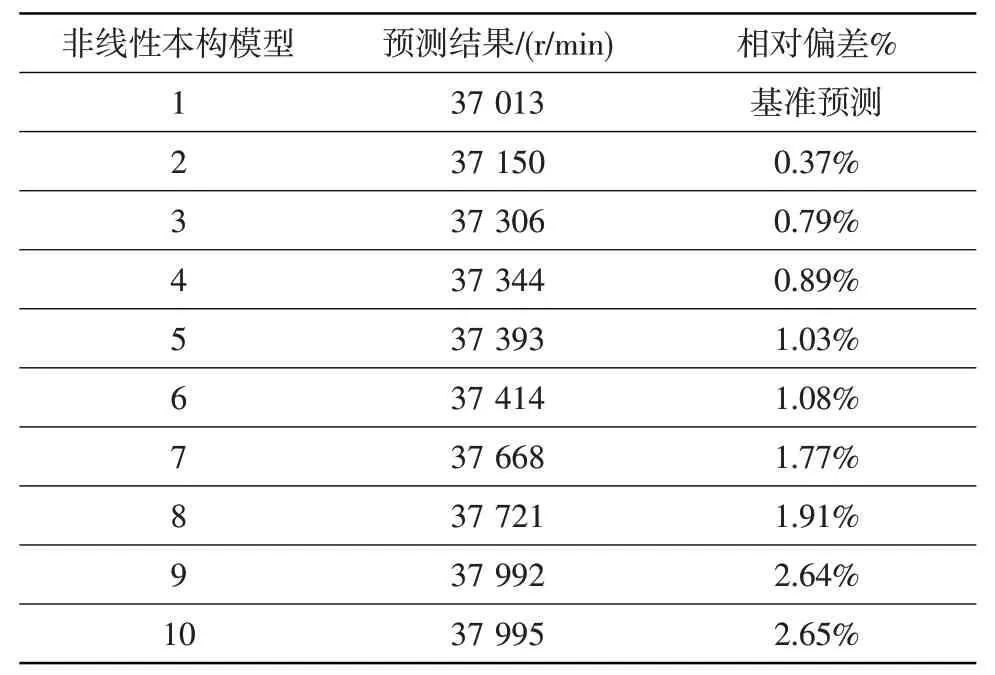
表6 各非線性本構模型的輪盤破裂轉速預測結果及對照Table 6 Prediction results of disc burst speed based on various non-linear models

5 結論

針對GH4169 輪盤，采用基于塑性失穩準則和大變形有限元分析方法，分別利用雙線性、多線性和非線性本構模型，計算分析了材料性能分散性對輪盤破裂轉速預測結果的影響。結果表明，在典型分散范圍內，材料性能分散性對輪盤破裂轉速預測結果有一定影響，但影響較小。采用基于塑性失穩準則和大變形有限元分析方法預測輪盤破裂轉速，可不考慮材料性能分散性造成的影響，直接采用材料最差性能真應力-真應變曲線進行預測，以獲得相對保守更為安全的結果。