基于傅里葉變換下的水銀測量元件的特性研究
劉宇軒,杜 苗,王 菁
(天水師范學院 電子信息與電氣工程學院,甘肅 天水 741000)
對于傳統的水銀溫度計而言存在著水銀膨脹系數的誤差、毛細管直徑不均勻的誤差、毛細管刻度的誤差、熱滯后的誤差、露莖的誤差等問題[1]。但是文章重點討論水銀本身性質上的問題。利用傅里葉分析,并且通過設計一個補償系統和去噪系統,可以有效地提高水銀溫度計的精度與使用效率。在家庭生活方面占據著不可忽視的地位,可以大大降低判斷身體溫度的失誤率。
1 傅里葉級數[2-3](Fourier Series)
對于一個由成諧波關系的復指數,是一種通過線性組合而成的信號,見式(1):
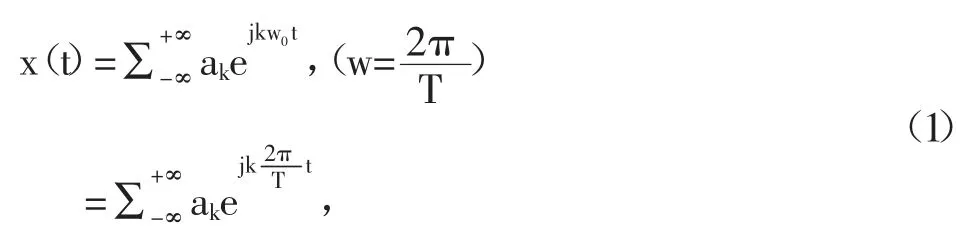

式(1)稱為傅里葉級數。此處ak的表達式為式(2):ak為傅里葉級數系數(Fourier Series Coefficient)。
2 傅里葉變換[2-3](Fourier Transform)
用傅里葉級數來表示一個周期信號時,當周期T逐漸增加時,該信號的基波頻率就會相應減少,對應的成諧波關系的各個分量在頻域上也會逐漸靠近;那么進一步的擴展開來,當周期T趨于無窮大的時候,這些頻率分量也就變成了一個連續域,從而在傅里葉級數求和的過程中,就演變成了求積分的問題。
對于一個信號x(t)來說,形如:

就稱為對函數x(t)進行傅里葉變換。那同樣的,它的逆變換為:

式(3)和式(4)稱為傅里葉變換對(Fourier Transform Pair)。函數X(jw)稱為x(t)的傅里葉變換或傅里葉積分(Fourier Integral)。則函數x(t)為X(jw)的逆變換,所以式(4)稱為傅里葉逆變換(Inverse Fourier Transform)。傅里葉變換是一種對于信號進行分析的工具,它既可以分解和分析信號,也可以將分解的信號合成為一個信號。一般情況下,傅里葉變換是用正弦波充當信號的主要成分。
3 逆系統(Inverse System)
當H(jw)*Y(jw)=1時,則這兩個系統互為逆系統。假如該系統在不同的信號激勵作用下產生了不同的響應,那么則稱該系統為可逆系統。并且對于每一個可逆系統來說,都存在一個逆系統。當原系統與這個逆系統級聯后,輸出信號與輸入信號則相同。
4 補償系統的設計(Design of Compensation System)
當把測量裝置的輸出提供給該補償系統時,其所產生的輸出等于待測量液體的瞬時溫度。假設這個裝置對溫度的響應為單位階躍響應,見式(5):

則該響階躍應的沖激響應,見式(6):

該系統的頻率響應,見式(7):
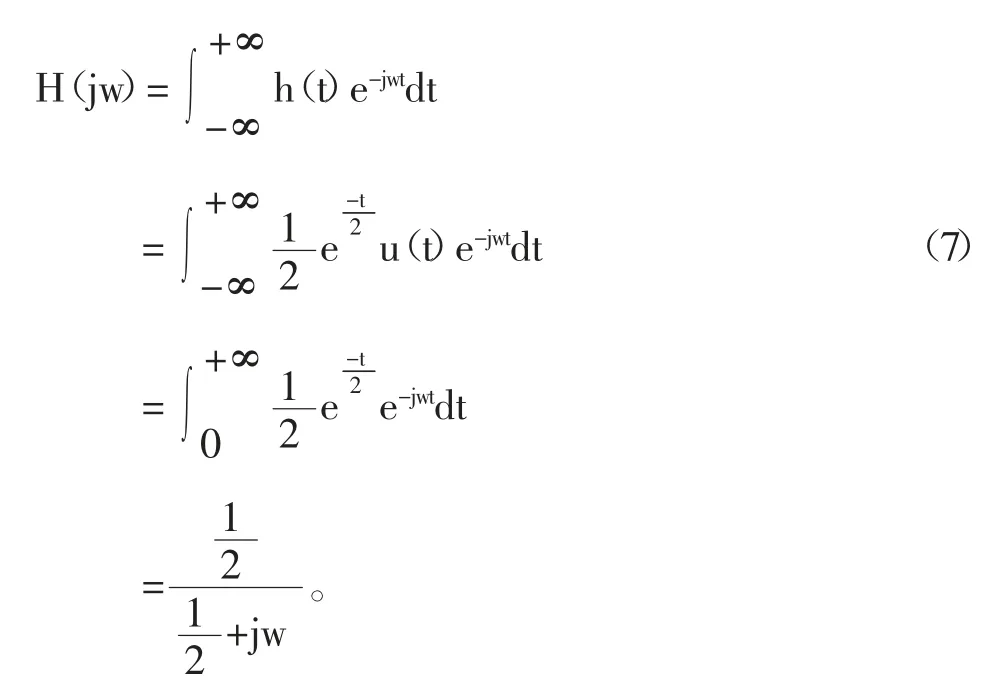
現在需對上方系統構建一個逆系統,因此該逆系統的頻率響應為G(jw),見式(8):
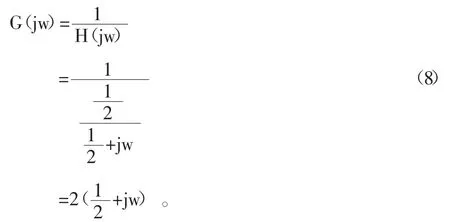
對G(jw)進行傅里葉逆變換得到式(9):

5 誤差分析(Error Analysis)
在周期信號中存在均方誤差,即
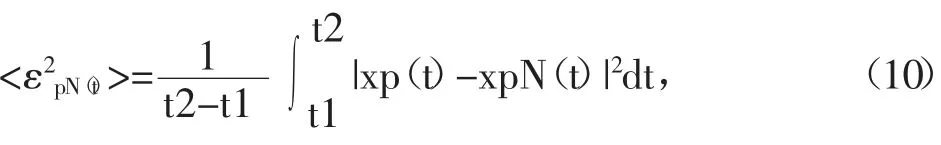

周期信號的最小均方誤差為

在把逆系統作為測量裝置的補償器時,常常發生的一個問題是:如果由于裝置內部發生了微小而且還無規律的一些現象,比如分子運動、化學變化等等[4]。就導致了測量裝置的實際總輸出可能會包含有一定程度的誤差,那么也可能會產生相對較大的讀數誤差。尤其對于溫度計這樣一種很敏感的醫療測量工具來說是無法接受的。但是往往在實際的系統當中,這種誤差源總是存在的,因此就必須要將這些誤差納入到考慮范圍當中,也就是要進行誤差分析。為了證明這一點,現在研究一個測量裝置,假定它的總輸出還是可以用式(5)所表示的測量裝置的響應s(t)與干擾“噪聲”信號n(t)之和來表示和模擬。該模擬的模型圖見圖1。
圖1中包括了逆系統,該系統以測量該裝置的總輸出作為輸入。假定n(t)=sin(wt),那么當n(t)通過該逆系統時,經傅里葉分析的計算可得輸出p(t)為式(13):
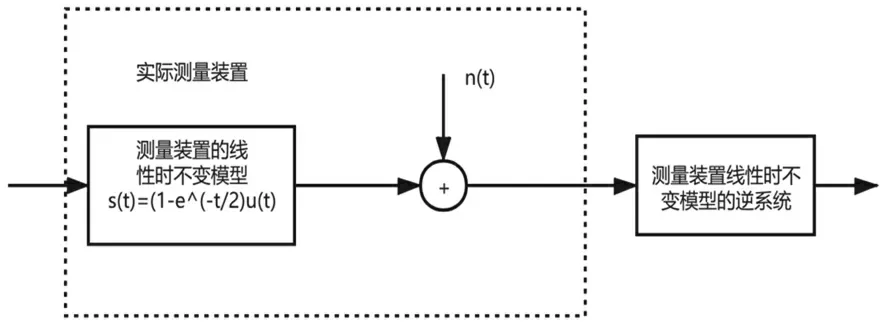
圖1 誤差分析的模型圖

顯然輸出是直接取決于w的取值,跟其他的值無關,滿足該系統為線性時不變系統這個條件。因此,隨著w的增加,噪聲對輸出的影響也會增大。
6 去噪系統(Denoising System)
對于水銀來說,水銀容易受到紫外線、輻射、高頻場直射等干擾[4],也就是干擾“噪聲”信號。干擾“噪聲”信號在許多線性時不變系統分析應用中是一個很重要,而且絕對不可忽視的問題。具體而言,要在系統的響應速度和系統抑制高頻干擾的能力之間進行基本的平衡。這種平衡意味著,如果提高測量裝置的響應速度,也就是采用前面所述加入一個逆系統。那么就產生了一個把那些不需要的正弦信號也放大了的系統。為了進一步說明,考慮一個測量裝置,它對被噪聲污損了的溫度變化做出了瞬時響應。這個系統的響應模型圖見圖2。
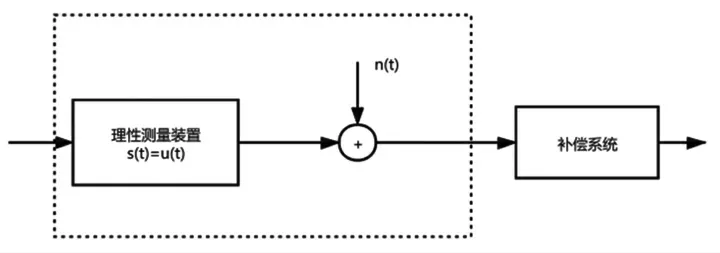
圖2 去噪系統模型圖
即該系統的響應可以利用理想化測量裝置的響應與污損信號n(t)的響應之和來表示。假如我們希望設計一個新的補償系統,該補償系統的作用就是可以減慢對實際溫度變化響應的同時,也衰減了噪聲n(t)。設這個補償系統的單位沖激響應(Unit Impulse Response)為式(14):

使得圖2的總系統在對噪聲n(t)=sin6t所產生的輸出幅度不大于1/4的情況下,對溫度階躍變化的響應盡最大可能的快。
對該系統的響應進行傅里葉變換得:
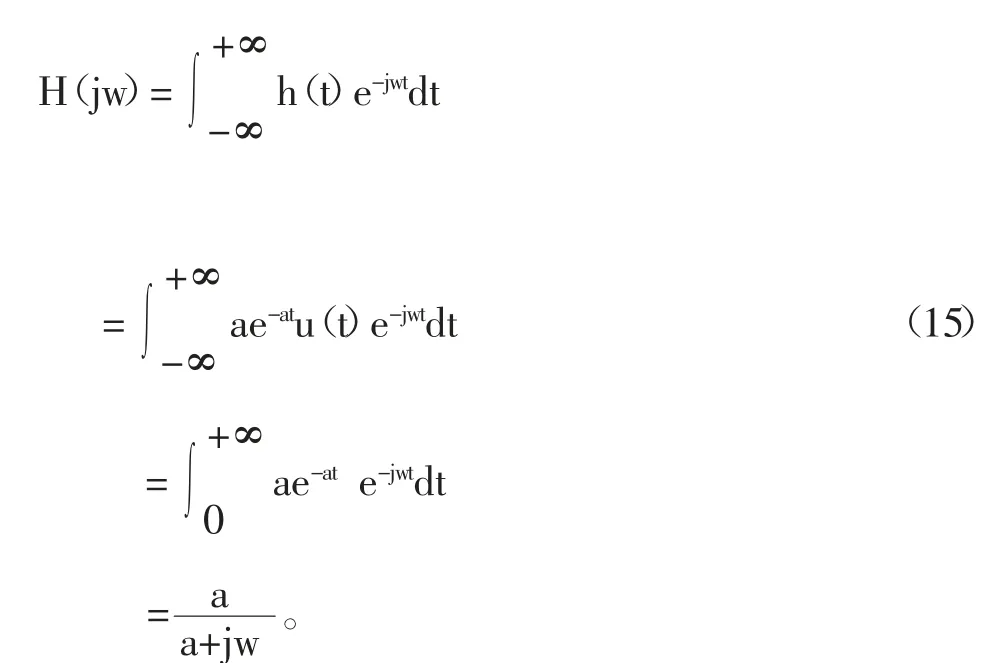
當|H(jw)|2≤,恰好當w=6的時候,即的時候,就可以得到。此時這個范圍內的a的取值才能使圖2中的總系統在對噪聲n(t)=sin(wt)(w值取6的時候)所產生的總輸出幅度不大于的條件下,對溫度的階躍變化的響應加快。也就是使得水銀溫度計受外界干擾的程度降低,那么自然該系統就穩定、精確。
7 結束語
對于溫度計當中水銀的一些特性,按照傳統的溫度計來看,該溫度計是無法快速做出反應的,但是利用傅里葉分析進行改進的話,可以最大限度地避免光線、熱輻射等[4]問題對它的影響,使得該溫度計會更加靈敏、測量精度更加高。通過設計一個補償系統和去噪系統,在水銀溫度計的靈敏度方面得到了很大提高,在日常家庭生活當中起到不小的作用。

