梯度提升回歸樹在風力發電機溫度預測的應用研究

江漢大學人工智能學院 陳 巖 侯 群 關雅琦

隨著全球范圍內風電裝機總量的逐步增加，風力發電領域對風機的運維提出了更高的要求。風力發電機的溫度是評價風機運行狀態的重要指標之一，其預測值可以用于風力發電機的故障預警等應用場景。本文介紹了一種基于梯度提升回歸樹對風力發電機溫度進行預測的方法，首先使用皮爾遜相關系數法選取發電機溫度的特征參數，利用正常工況下的歷史數據，使用梯度提升回歸樹建立發電機溫度的歸回預測模型，最后將采集的實時運行數據輸入到該模型中，得到對應的發電機溫度預測值。本文通過實驗，有效并準確地預測了風力發電機的溫度值，擬合度達到96.42%，為進一步的風力發電機溫度測點預警提供了準確的數據來源。

發電機溫度是風力發電系統中極為重要的指標之一，它的預測值可以用于風場運維中的故障預警場景。在風電機組運行的過程中，每個部件上都裝有對應的數據采集傳感器用于實時數據的采集。然而，即使是當前的運行數據是正常的，也并不能說明該風機指標在長期的運行趨勢中是正常的，這就需要使用機器學習建模的方法來對實時的運行數據進行預測，判斷其與真實數據的偏差程度，如果偏差過大，則代表風機在將來的某個時間點將會發生故障。如果可以提前預測出發電機會因為溫度過高而出現故障，將有助于風電場及時做出檢修計劃，排查故障原因，避免造成經濟損失和生產事故。

從目前的風電運維領域，很多專家學者都在嘗試使用機器學習、深度學習和神經網絡建模等方法對溫度進行預測。溫度值的預測不僅僅是針對發電機的溫度，還有齒輪箱各個部件的溫度以及環境溫度等。滕偉等提出了一種基于極端梯度提升樹于長短時記憶網絡加權融合的組合模型對風力發電機的定子繞組溫度進行了預測。梁濤等提出了一種基于灰色關聯度理論的變權組合預測模型對齒輪箱溫度進行預測。劉午超建立了用于風力發電機溫度預測的小波神經網絡模型，通過相關系數法對風力發電機溫度的影響因素進行分析。

本文使用了種集成學習中的梯度提升回歸樹算法，探討其在風力發電機溫度預測中的應用研究，將發電機溫度的歷史數據及其對應的特征參數數據進行訓練建模，并使用測試數據集對預測模型進行檢驗。

1 梯度提升回歸樹算法介紹

梯度提升樹也可以稱為多決策樹。根據不同的目的，通常分為梯度決策提升樹（GBDT,Gradient Boost Decision Tree）和梯度提升回歸樹（GBRT，Gradient Boost Regression Tree）。該算法由Friedman在20世紀初提出，具有很強的非線性擬合能力，常用于設備運行預測、人流預測等不同場景。

梯度提升回歸樹由多個決策樹組成，為了得到最終結果，只需將所有決策樹的輸出結果相加即可。它的核心是每棵樹都是從之前所有樹的殘差中學習出來的。為了防止過擬合，增加了Boosting過程。

原始的Boost算法會給每一個樣本都賦予一個相同的權重，然后開始對模型進行訓練。在這個過程中，每一步的模型都會導致樣本出現正確或錯誤。在這時對模型中的點進行標記，如果模型是往正確的方向前進的，那么就減少它的權重，如果是往錯誤的方向前進的，那么就增加它的權重。這樣，經過n次迭代，錯誤的點由于擁有過高的權重，會被重點關注，并且我們得到了n個簡單的分類器，將它們組合起來，便可以得到最終的模型。

Gradient Boost和傳統的Boost有所不同，在每一次計算的過程中，它會在誤差減少的方向上建立新的模型，這樣在經過n次迭代的過程中，我們每一步都在減少誤差的方向上前進。

梯度提升回歸樹作為一種集成學習方法，有如下優點：

（1）在參數調整時間相對較小的情況下，預測精度較高；

（2）非線性數據處理能力強；

（3）可以靈活處理各種類型的數據，包括連續值和離散值；

（4）利用一些魯棒損失函數，對異常值的魯棒性非常強；

（5）不需要數據歸一化。

同時，梯度提升回歸樹也具有一些缺點，比如難以并行訓練數據、不適合高維稀疏特征等。

2 基于梯度提升回歸的風力發電機溫度預測模型

2.1 特征參數的選取

在統計學中，皮爾遜相關系數(Pearson correlation coefficient)，又稱皮爾遜積矩相關系數(Pearson product-moment correlation coefficient，簡稱PPMCC或PCCs)，是用于衡量兩個變量之間的相關性，其值介于-1與1之間。

兩個變量之間的皮爾遜相關系數定義為兩個變量之間的協方差和標準差的商：

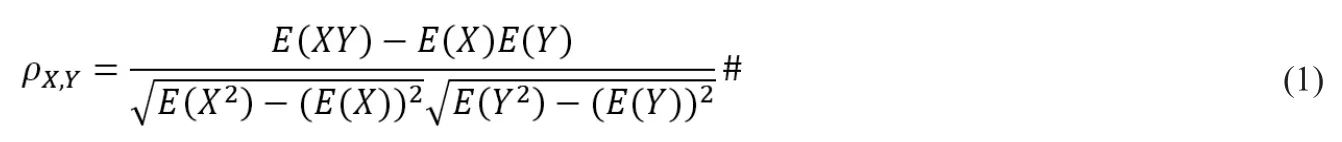
對于樣本皮爾遜相關系數，給出其簡單的單流程算法：

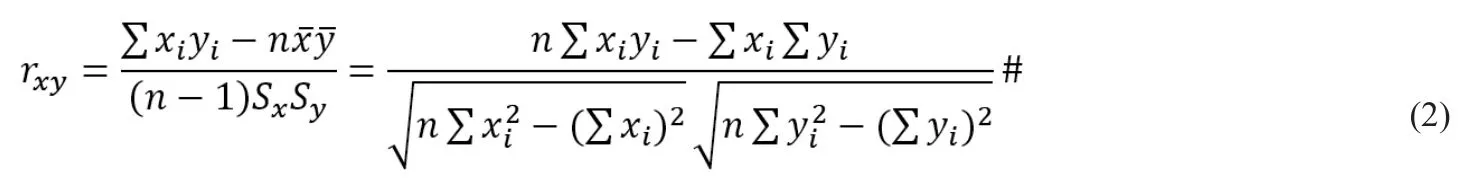
將某一時間段風機正常工況運行狀態下的發電機溫度監測數據提取出來作為X，將其他同一時刻具有相關性的觀測特征數據提取出來作為Y，分別代入公式(7)，可以得到X關于Y的皮爾森相關系數ρX,Y。

將特征參數和發電機溫度的連續數據處理為兩個觀測向量，代入公式(7)，即可得到發電機溫度關于該特征參數的皮爾遜相關系數，如表1所示。

表1 發電機定子溫度特征參數選取表

2.2 使用梯度提升回歸樹建立預測模型

針對梯度提升回歸，首先要輸入訓練集樣本：

其中，最大迭代次數T，損失函數L。

初始化弱學習器：

在迭代輪數從1到T的過程中，對樣本i=1,2,…,m，計算負梯度：

針對每一個葉子節點里的樣本，求出使損失函數最小，擬合葉子節點最好的輸出值ctj值如下：

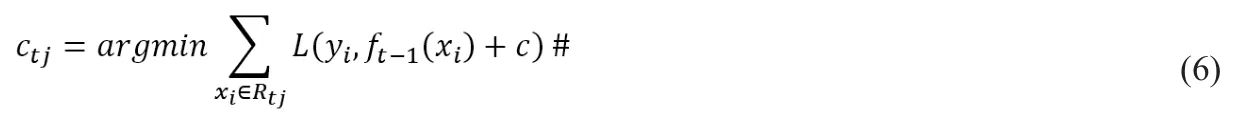
更新強學習器：

從而得到最終的強學習器表達式：

通過對正常工況下歷史數據的訓練，調整最適合的迭代次數，即可得到最佳的風力發電機溫度預測模型。在這里，使用sklearn下的ensemble集成學習功能包，調用GradientBoostingRegressor()方法，不斷調整參數，得到最后的迭代次數n_estimators值為200。整個預測模型的流程圖如圖1所示。

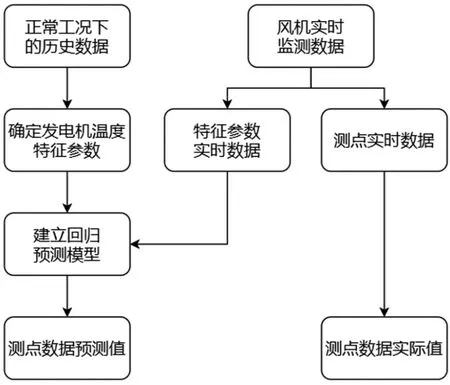
圖1 預測模型流程圖

3 預測結果分析

3.1 模型訓練結果

本文選取某風電場2019年4月1日12:00—18:00，6h內的60s采樣間隔數據，在得到預測模型時后，使用方根均差、平均絕對誤差和擬合度作為其評價標準。在訓練結束后，得到測試集的擬合度為96.42%，其中方根均差為0.20，平均絕對誤差為0.15。模型預測的真實值和預測值圖如圖2所示。

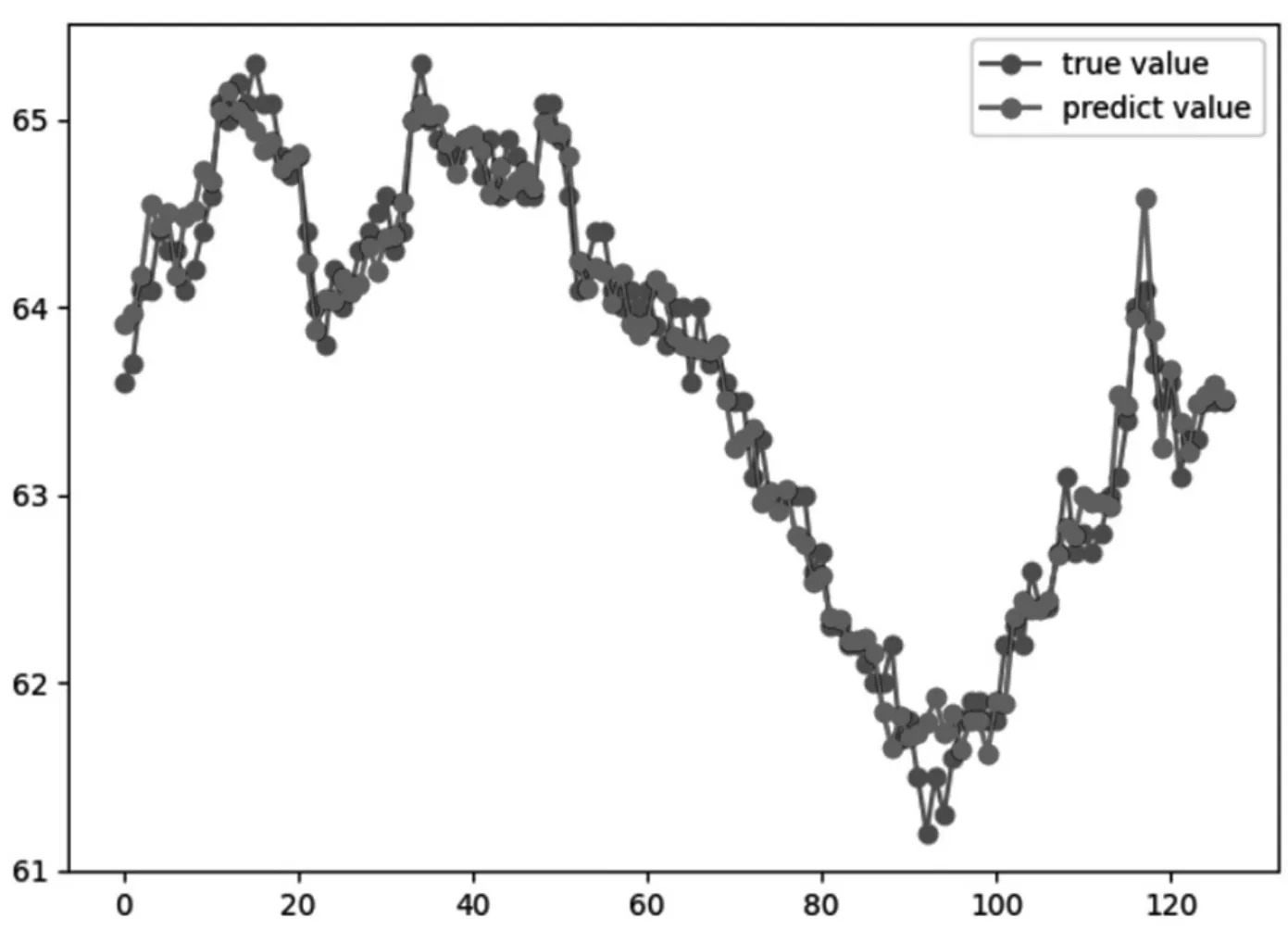
圖2 基于梯度提升回歸樹的預測值與真實值

3.2 模型校驗

為了進一步對基于梯度提升回歸樹的發電機溫度預測模型精度進行評價，本文使用BP神經網絡算法建立預測模型與其進行對比。使用相同的數據集，使用BP神經網絡算法建立發電機溫度預測模型，得到測試集的擬合度為96.15%，其中方根均差為0.21，平均絕對誤差為0.16。模型預測的真實值和預測值圖如圖3所示。

圖3 基于BP神經網絡的預測值與真實值

風力發電機機組設備數據預警是風電運維過程中極其重要的環節，包括發電機溫度等指標的預測。在風力發電機的運行過程中，有很多因素會對發電機溫度產生影響，所以選取這些主要因素作為特征參數考慮進來并對結果進行預測成為了關鍵的一步。本文首先使用皮爾遜相關系數法對發電機溫度的特征參數進行選取，再使用梯度提升回歸算法將正常工況下的發電機溫度歷史數據及其特征參數數據訓練出預測模型，便可以得到預測結果。將該模型的預測結果與實際值相比，擬合度為96.42%。同時，使用BP神經網絡算法對同樣的參數指標和數據進行預測，可以得到略低于使用梯度提升回歸樹算法訓練的預測模型的擬合精度，側面證明了使用梯度提升回歸樹算法再風電運行數據預測領域的可行性。