改進遺傳算法優化RBF神經網絡在短期電力負荷預測中的應用

武漢市規劃研究院 宋朝鵬

為減小短期電力負荷預測中的誤差，提出了一種改進遺傳算法優化RBF神經網絡（IGA-RBF）的負荷預測方法，解決RBF神經網絡易陷入局部極值的問題，提高預測的準確性。利用IGA算法對RBF神經網絡的中心、寬度以及隱含層與輸出層之間的聯結權值參數進行優化，提高了RBF神經網絡的泛化能力。仿真實驗表明，IGA-RBF算法在短期電力負荷預測中具有較快的收斂速度和較高的精度，具有較好的實用價值。

短期負荷預測是電力系統負荷預測的重要內容，精準的電力負荷預測對于制定發電計劃、保障生產生活用電、控制電網經濟運行、降低旋轉儲備容量等方面具有重要作用。

隨著現代人工智能算法的快速發展，粗糙集、人工神經網絡、群體進化算法等智能化方法被廣泛應用于電力負荷預測之中。徑向基函數（Radial Basis Function，RBF）神經網絡可映射復雜的非線性關系，魯棒性好且自學習能力強大。因此，RBF神經網絡被廣泛應用到電力系統短期負荷預測。但RBF神經網絡也存在易陷入局部最優解的問題，使得預測精度下降。針對RBF網絡存在的問題，本文利用改進遺傳算法(Improved Genetic Algorithm，IGA)強大的進化尋優能力，提出一種IGA-RBF神經網絡短期負荷預測模型，該方法可有效解決RBF神經網絡訓練時易陷入局部極值的問題，提高算法收斂精度。

1 RBF神經網絡的結構與原理

RBF神經網絡是一種三層前向神經網絡，網絡的拓撲結構如圖1所示。第一層是輸入層，為信號源節點；第二層是隱含層，其單元數根據實際需要來確定；第三層是輸出層，是對輸入數據產生的響應。圖1所示RBF神經網絡的結構中，x=[x1,x2,...,xn]T為網絡的n維輸入，y=[y1,y2,...,ym]T為網絡的m維輸出，c=[c1,c2,...,ch]T為隱含層基函數中心構成的矩陣，為隱含層徑向基函數，Whm∈Rh*m為隱含層至輸出層的聯結權值矩陣，b=[b1,b2,...,bm]T為網絡的閥值向量。

本文使用歐式距離函數作為RBF神經網絡的隱含層節點基函數，激活函數采用徑向基函數。在不同的徑向基函數中，高斯函數應用最廣泛，具有徑向對稱、解析性好并存在任意階導數的特點，本文以高斯函數為徑向基函數，則圖1所示的RBF神經網絡輸出表達式可表示為：

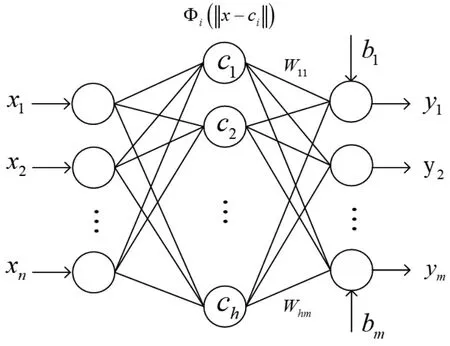
圖1 RBF神經網絡結構圖

2 改進遺傳算法優化RBF神經網絡模型

RBF神經網絡有三個重要的參數：即徑向基函數的中心ci與寬度δi，聯結權值wij。合理確定這些參數對于RBF神經網絡性能的發揮至關重要。但是，目前隨機選取固定中心法、自組織學習法和梯度下降法等常規學習規則存在著需大量的樣本數據、易陷入局部極值等缺陷。因此，本文將IGA算法引入到RBF神經網絡的參數尋優，有效解決RBF神經網絡訓練時易陷入局部極值的問題。

遺傳算法是一種啟發式全局搜索算法，具有較高的搜索效率和優異的全局優化性能，其交叉概率Pc和變異概率Pm的選取對于收斂性有著重要影響，參數選取不合適將造成算法過早收斂。因此，本文采用改進的自適應遺傳算法，交叉概率和變異概率隨適應度自動改變調整，以達到更好的收斂性。

2.1 確定編碼方式

本文選用實數編碼方法，把徑向基函數的中心ci、寬度δi及輸出層的聯結權值wij編成染色體，用實數來表示每個個體的基因值。基因值編碼方式為：

其中：h為隱含層神經元個數，n為網絡的n維輸入，m表示網絡的m維輸出。

2.2 選擇適應度函數

采用適應度函數評價群體中各個染色體的優劣。網絡優化的目標是搜尋到一組最優參數，使得運算的均方根誤差最小，本文的適應度函數選為：

式中，k為訓練樣本總數，m為網絡輸出層神經元個數，sij為神經元理想輸出值，yij為神經元實際輸出值。

2.3 交叉與變異

交叉和變異用于從當前群體中產生下一代新群體。若子個體的適應度小于父個體適應度，代表子代優于父代，則用子個體代替父個體。如此重復迭代，直到達到最大迭代次數或滿足給定的精度為止。

在傳統遺傳算法中，交叉率Pc與變異率Pm在算法執行過程中均保持不變，易產生過早收斂而陷入局部極值的情況。因此，需要在運算過程中根據當前個體適應度及迭代次數，對交叉概率和變異概率進行自適應動態調整。在尋優過程中，當個體適應度大于平均適應度時，說明個體性能不佳，應當采用較大的交叉概率和變異概率；若個體適應度小于平均適應度，則表明個體性能優異，應結合其適應度選取交叉概率與變異概率。因此，本文交叉概率Pc和變異概率Pm采用如下計算公式：

式中：Pc1=0.8；Pc2=0.6；Pm1=0.1，Pm2=0.01，f’為要交叉的兩個體中較小的適應度值；f為要變異的個體適應度值；favg為每代群體平均適應度值，fmin為群體中的最小適應度值。

2.4 預測應用

將IGA優化所得的最優個體作為RBF神經網絡最優的參數值，并進行負荷預測仿真測試。

3 預測模型性能分析

為驗證算法的有效性，現采用Matlab對IGA-RBF算法與RBF算法分別進行仿真測試。

3.1 輸入輸出量設定

IGA-RBF網絡采用三層結構，即輸入層、隱含層和輸出層。結合不同因素對電力負荷的影響，將預測日最高溫度、預測日最低溫度、預測日日期性質、預測日期前一天最大負荷、預測日期前兩天最大負荷、預測日期上一周同一天最大負荷6個變量作為輸入變量，預測日最大負荷預測值為輸出變量。

3.2 仿真測試

本文選取某地區2019年6、7、8、9共4個月的110組電力負荷數據作為訓練數據，并選取該地區2020年6、7月份的50組電力負荷數據作為預測數據對模型進行測試。初始種群規模設為35，訓練誤差為0.001，最大迭代步數為1000步。

訓練均方根誤差隨迭代次數變化情況如圖2、圖3所示。由圖可知，基本RBF神經網絡收斂速度較慢，而采用改進遺傳算法優化的RBF神經網絡進行訓練，收斂速度明顯較快且收斂精度更高。

圖2 RBF算法收斂曲線

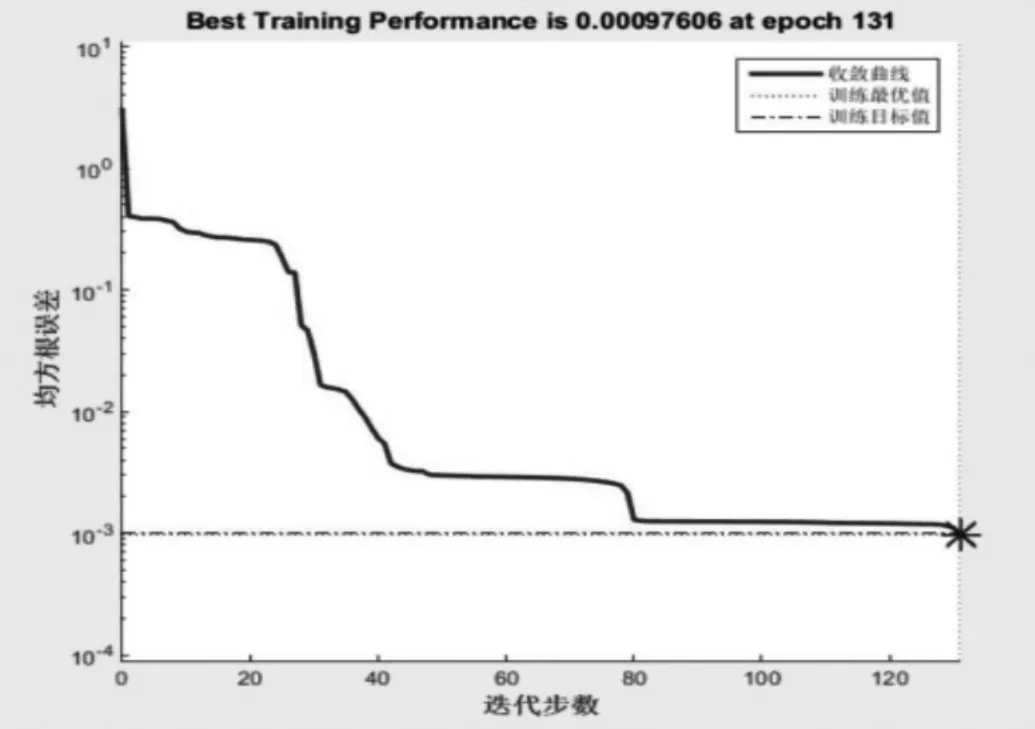
圖3 IGA-RBF算法收斂曲線

將IGA-RBF神經網絡算法與RBF神經網絡算法測試結果進行比較，IGA-RBF算法與RBF算法平均誤差分別為1.9%和3.9%，表1為部分測試結果。從表中數據可以看出，IGA-RBF算法的誤差相對較小，性能優于RBF算法，其預測精度更高。

表1 測試結果對比表（部分）

針對RBF神經網絡在短期電力負荷預測中存在易陷入局部極值的問題，本文提出一種改進遺傳算法優化RBF神經網絡模型。通過仿真分析，IGA-RBF神經網絡的收斂能力更強，預測誤差更小，性能更優，在電力系統短期負荷預測中有著更好的實用性。