基于MRE 隔振器的變剛度半主動隔振系統分析

黃學功，劉濤，馬偉佳，張廣

（南京理工大學 機械工程學院，江蘇 南京 210094）

磁流變彈性體（Magnetorheological Elastomer，MRE）是磁流變材料的一種，一般是在基體材料（如橡膠等高分子聚合物）中添加微米級的軟磁性顆粒，經過一系列工序制成[1-3].1996 年Jolly 團隊[4]首次將軟磁顆粒加入到高分子聚合物中得到了最初的磁流變彈性體，并測試得到了磁流變彈性體在施加磁場后的力學性能變化響應時間為毫秒級別.加拿大學者Dargahi 等[5]用硅橡膠作為基體，加入體積分數為40%的羰基鐵粉制成磁流變彈性體材料，當磁感應強度從0 T 增加到0.45 T 時，相對磁流變效應達到了1 672%.近年來，隨著磁流變彈性體性能的提升，其響應速度快、高磁流變效應的特點受到了越來越多的關注，已經成為土木工程、結構振動控制領域研究的熱點.

磁流變彈性體隔震支座使用磁流變彈性體材料代替傳統橡膠材料，可以通過磁感應的強弱來改變支座的剛度，相較于傳統橡膠隔震支座擁有了可控性.悉尼科技大學的Li 等[6]和Gu 等[7]根據傳統的疊層橡膠隔振器設計了一款疊層MRE 隔振支座，并進行了一系列實驗研究，根據測試，該隔振器的最大水平剪切位移為26 mm，在零磁場強度的情況下縱向承載力可達到370 kg.馬來西亞理工大學的Wahab等[8]利用天然橡膠基MRE 制作了一臺大型的應用于實際建筑隔振的基礎隔震支座，其中詳細介紹了支座的設計加工過程，MRE 疊層結構的焊接工藝，具有很高的實用價值.測試表明，當工作電流從0 A 增加到3 A 時，支座的靜態豎向承載力增加了14%，動態豎向承載力增加了16%.

現有研究中，磁流變彈性體隔震支座大多采用半主動控制機制.近些年，國內外學者對基于磁流變彈性體隔震支座的半主動控制算法進行了大量研究.Eem 等[9]提出基于模糊控制的半主動控制算法，并通過試驗，驗證了其對結構的減震效果.Xu 等[10]提出了基于磁流變彈性體隔振支座的改進半主動變剛度控制算法，該算法充分利用支座的連續變剛度特性，控制效果良好.悉尼科技大學的Gu 等[7]提出了基于神經網絡控制的模糊控制算法，并進行了隔振控制試驗，結果表明，該控制算法有很好的控制效果.

目前對MRE 隔振器的研究大多為正向變剛度MRE 隔振器，對負剛度MRE 隔振器的研究較少.負剛度MRE 隔振器有效解決了正向變剛度MRE 隔振器在沒有振動的情況下也需要一直通電的問題，更加符合實際工程應用要求，因此對負剛度MRE 隔振器進行全面研究具有極高的工程價值.本文基于制備的磁流變彈性體材料，設計了一款面向橫向振動的負剛度隔振器，并進行了性能測試試驗.基于負剛度隔振器搭建了變剛度半主動隔振控制系統，設計了GA 模糊控制算法并進行了仿真分析.

1 MRE 隔振器設計與試驗方法

1.1 磁流變彈性體制備與測試

1.1.1 磁流變彈性體制備

磁流變彈性體的制備分三個過程：材料的充分混合、預磁化處理以及室溫下的固化.具體過程如圖1 所示，先將羰基鐵粉、硅橡膠和二甲基硅油按質量比為8 ∶1 ∶1 倒入燒杯中，充分攪拌使其混合均勻；然后將材料放入真空桶，抽出材料中的氣泡，這一步需反復多次抽取；倒入模具，蓋上模具端蓋，放在磁感應強度為600 mT 的加磁裝置中進行預磁化處理，預磁化的目的是為了提高MRE 的磁流變效應，研究表明，預磁化的MRE 可以產生更加明顯的磁流變效應以及更大的磁致模量[11]；加磁2 h 后放置常溫干燥環境5～7 d，即能脫模完成MRE 樣品的制備.

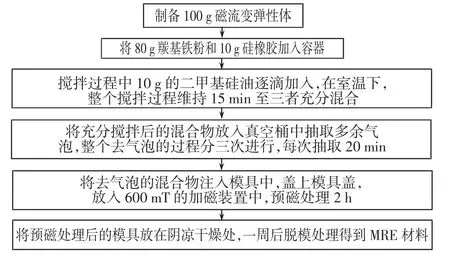
圖1 MRE 制備過程Fig.1 MRE preparation process

1.1.2 磁流變彈性體性能測試

將制備好的MRE 樣品置于如圖2 所示的測試儀器中，測試儀器為流變儀（型號：MCR302，Anton Paar），根據儀器的要求，將MRE 材料制成直徑為20 mm，厚度為1 mm 的圓形薄片，將MRE 樣品置于轉子與下盤片之間.由于MRE 要應用于MRE 隔振器中，在工作過程中處于動態應變條件，需要研究MRE 材料在動態應變下的特性才能更好地服務于MRE 隔振器.整個測試過程，MRE 薄片處于剪切工作模式，這與后續的隔振器工作模式一致.通過計算機設定室溫下測量，流變儀自帶的溫控系統可以設置溫度恒定；設置不同的工作條件，然后將測試結果存檔.本次測試MRE 性能的測試條件為：室溫25 ℃恒定，測試頻率設置為8 Hz，應變條件設置為0.1%、0.5%、1%.磁場強度從0 T 開始持續增加，直到MRE材料的儲能模量趨于穩定不變為止.

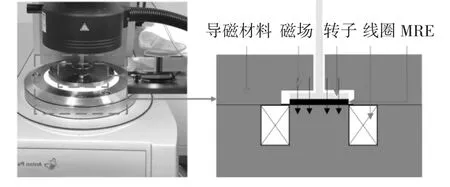
圖2 流變儀測試原理Fig.2 Testing principle of rheometer

圖3（a）為在不同應變條件作用下MRE 的剪切儲能模量與磁感應強度之間的關系.從圖中可以看出，MRE 的剪切儲能模量隨磁感應強度呈非線性增長趨勢，在磁感應強度為600 mT 時趨于穩定，在800 mT 時達到穩定值.其中在0.1%應變條件下儲能模量最大，達到2.95 MPa，隨著應變的增加，儲能模量會隨之降低，當應變為1%時，儲能模量最大為2.15 MPa，較0.1%應變條件，儲能模量衰減了27.6%，隨著應變的增大，衰減會更加嚴重，這是Payne 效應造成的，隨著應變的增加，粘彈性材料的動態模量會減小.圖3（b）是不同應變條件下MRE的磁流變效應隨磁感應強度的變化圖，從圖中可以看出，在小應變情況下，磁流變效應很大.當應變條件為0.1%時，磁流變效應最大可達到2 040%.換言之，在該應變條件下，當磁感應強度達到600 mT 以上時，MRE 的剪切儲能模量增加了20 倍.高磁流變效應是實際工程應用的關鍵，可以讓磁控條件降低，降低了外部磁場發生裝置的設計難度.

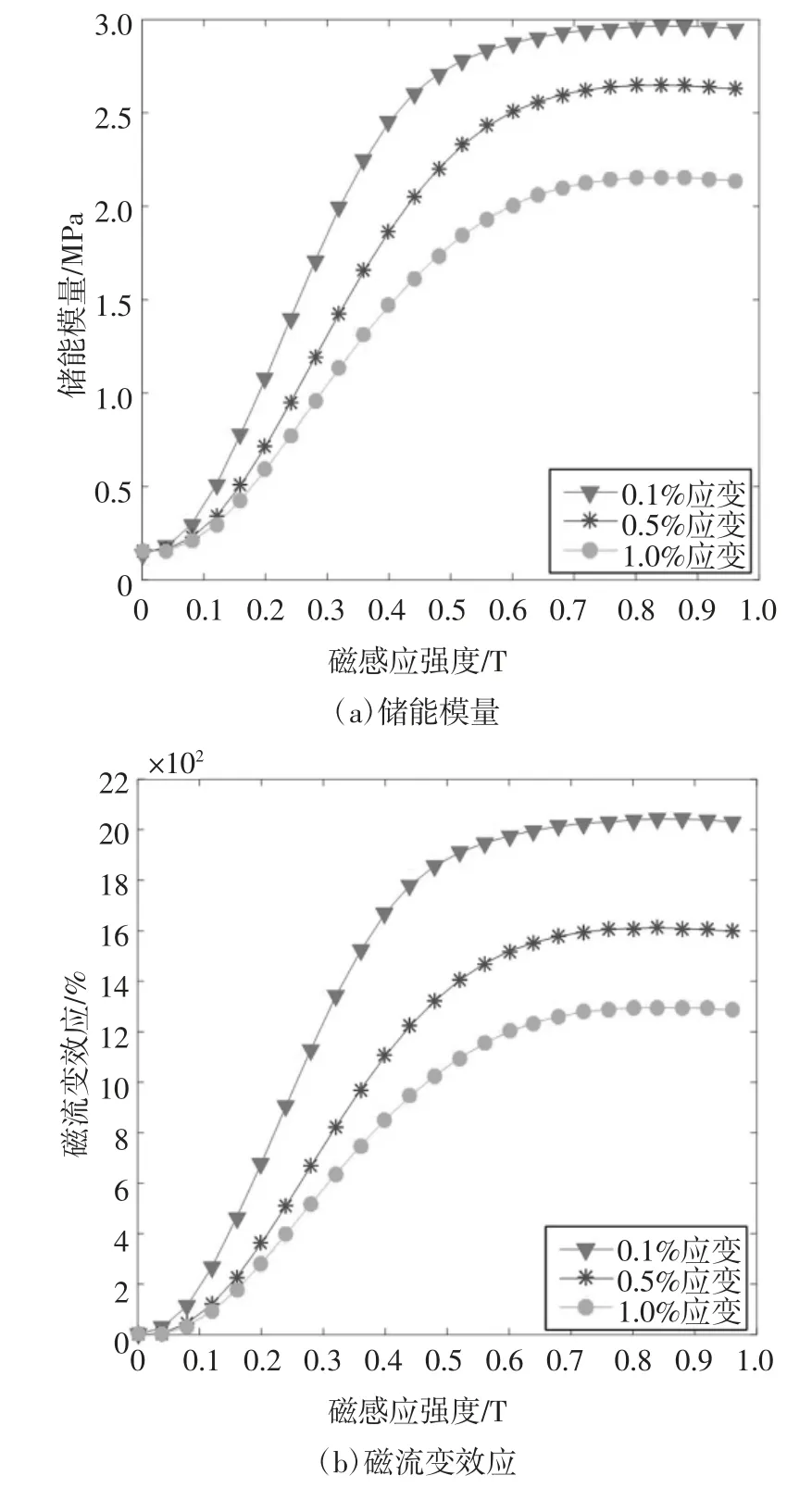
圖3 材料特性與磁場關系Fig.3 Relationship between material properties and magnetic field

1.2 MRE 隔振器的設計與測試

1.2.1 MRE 隔振器的設計

隔振器的具體設計過程參考文獻[12].隔振器的實物模型、具體結構組成以及工作原理如圖4 所示.其中永磁鐵提供一定大小的磁場，使隔振器具有較大的初始剛度，在正常工作環境中能夠承受較大的載荷，通過調節通入線圈電流的大小來改變隔振器的內部磁場環境，核心部分就是MRE 疊層結構，通過內部磁感應強度的大小來改變此結構的剛度和阻尼大小，進而達到隔振的目的.

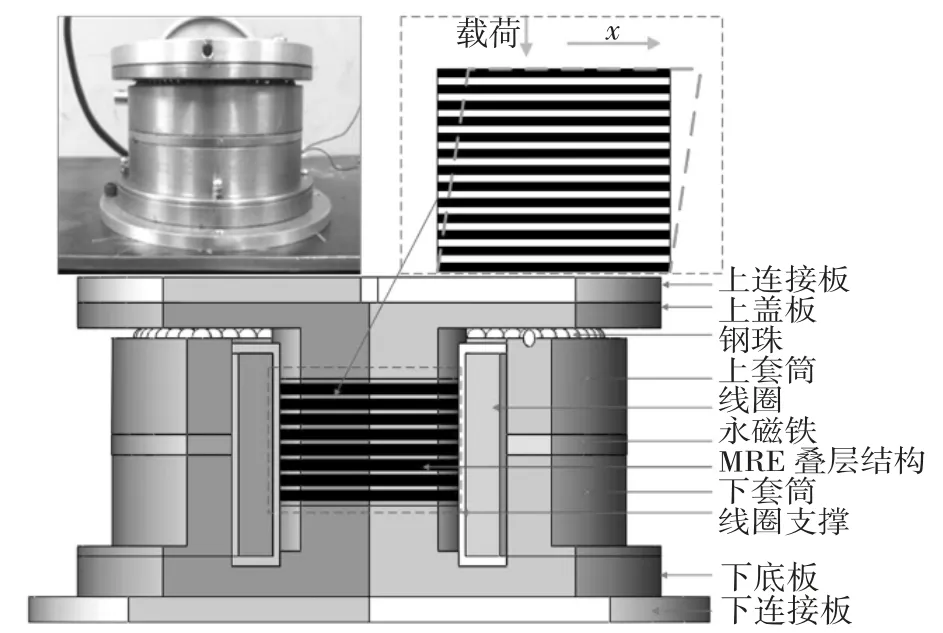
圖4 隔振器結構及原理Fig.4 Structure and principle of vibration isolator

1.2.2 MRE 隔振器的移頻特性測試

由于MRE 隔振器的固有頻率隨著外加磁場的變化而連續、快速變化，為了更好研究其隔振性能及其隔振控制規律，有必要進行相應的試驗來對其移頻特性進行測試.圖5 為本文所搭建的MRE 隔振器移頻特性測試試驗平臺，信號發生器發出的信號經由功率放大器放大后驅動激振器推著水平滑臺進行受迫振動，MRE 隔振器安裝于水平滑臺之上，兩個加速度傳感器分別安裝于MRE 隔振器上和水平滑臺上，用于測得激勵和響應加速度信號，所測得的加速度信號經電荷放大器轉變為電壓型加速度信號后傳入LMS 動態測試系統，LMS 動態測試系統對信號進行分析處理后最終傳至PC，整個過程中，由直流電源給MRE 隔振器供電.

圖5 移頻特性測試平臺Fig.5 Frequency shift characteristic test platform

根據試驗數據得到如圖6 所示的加速度傳遞率曲線，在-3 A、-1 A、1 A、3 A 電流下隔振器的共振頻率分別為68 Hz、63 Hz、59 Hz 和50 Hz.因此，可以得出在-3～3 A 的電流范圍內MRE 隔振器的共振頻率隨著勵磁電流的增加而減小，由-3 A 時的68 Hz 減小到3 A 時的50 Hz，減小了18 Hz，隔振器的共振頻率發生了明顯的負向移頻.這是由于作用于MRE 的磁場是由勵磁電流激發的磁場和永磁體所產生的磁場疊加而成的，當兩個磁場的方向相反且勵磁電流所激發的磁場小于永磁體的矯頑力時，勵磁電流的值越大，疊加磁場的強度就越小，MRE 的剛度就越小，從而隔振器的共振頻率就越小.當兩個磁場的方向相同時，勵磁電流的值越大，疊加磁場的強度就越大，MRE 的剛度就越大，從而隔振器的共振頻率就越大.

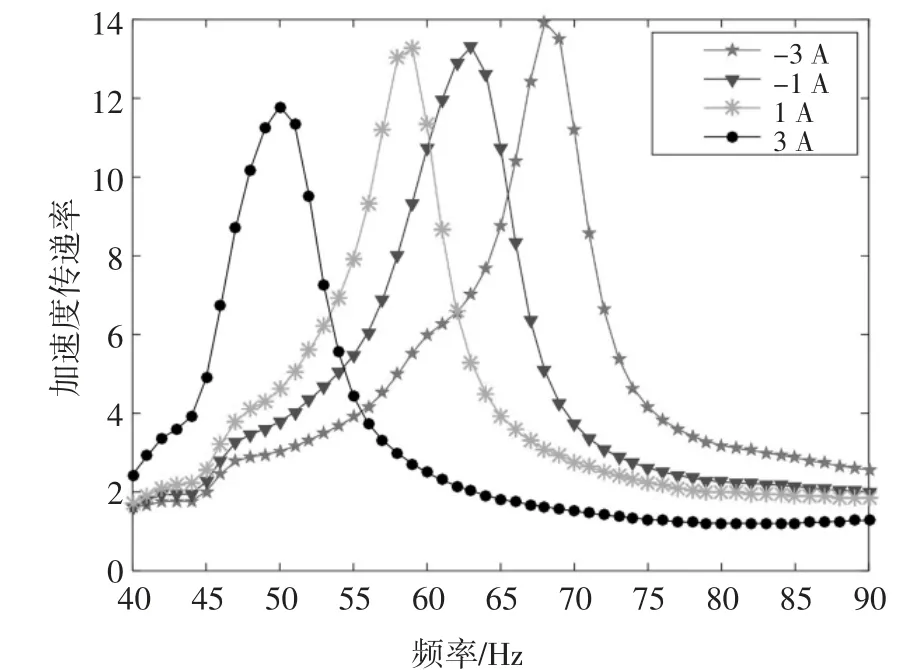
圖6 移頻特性曲線Fig.6 Frequency shift characteristic curve

1.2.3 MRE 隔振器的參數計算

隔振器的簡化模型可以用一個單自由度模型來描述，如圖7 所示.根據模型可以建立運動方程：

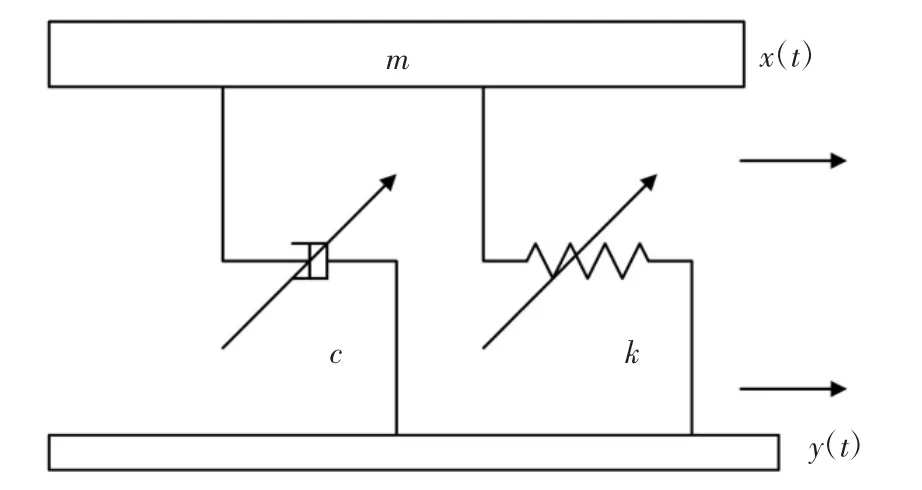
圖7 隔振器單自由度模型Fig.7 Single degree of freedom model of vibration isolator

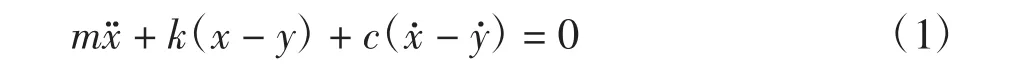
式中：m 為負載質量；k 和c 分別為MRE 隔振器的剛度和阻尼；y 和x 分別為激勵位移和響應位移；y和x分別為激勵速度和響應速度；x 為響應加速度.

已知單自由度有阻尼系統的傳遞率函數表達式為：

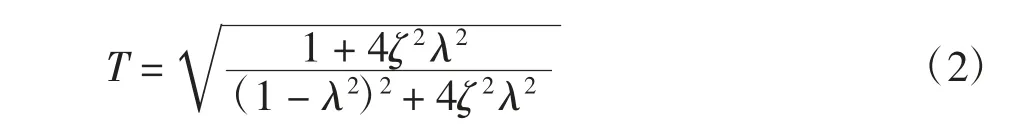
對于有阻尼單自由度振動系統來說，其共振頻率為：

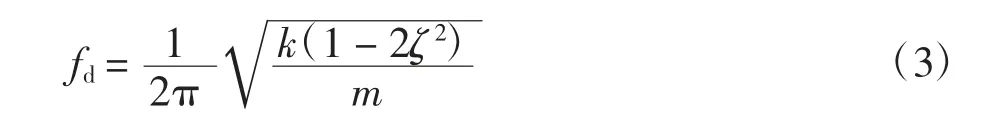
式中：fd為該隔振系統的共振頻率.

通過式（2）計算得到的系統阻尼比ζ 和試驗測得的共振頻率fd，利用式（3）可以計算系統的等效剛度，再由阻尼比公式可以得到系統的等效阻尼.

本次測試的負載質量為0.75 kg，結合圖6 可以得到MRE 隔振器在不同電流下的性能參數如表1所示.Tm為傳遞率最大值，從表1 可以看出，隨著電流的增加，隔振器的剛度和阻尼隨之減小.其中，變剛度特性明顯，阻尼變化不明顯.圖8 為隔振器剛度隨電流變化曲線，由圖8 可得，剛度隨電流基本呈線性變化關系，擬合曲線的關系式為：

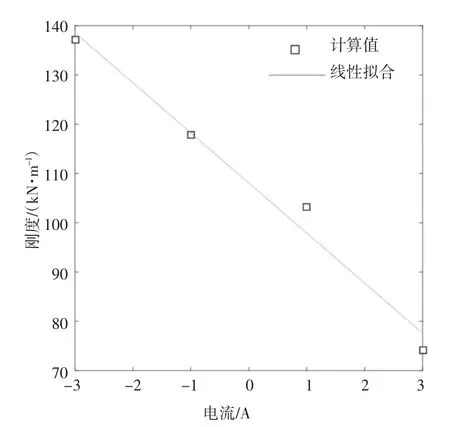
圖8 剛度線性擬合曲線Fig.8 Stiffness linear fitting curve

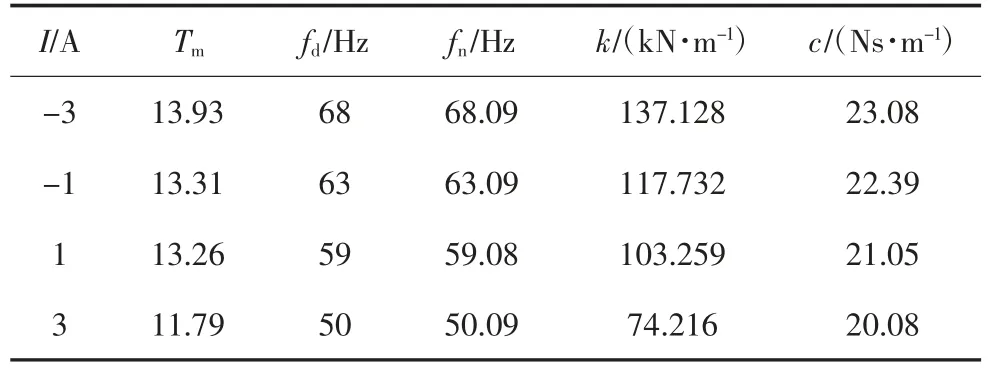
表1 MRE 隔振器的性能參數Tab.1 Performance parameters of MRE isolator

2 基于MRE 隔振器的半主動隔振系統

2.1 地震作用下變剛度隔振系統的動力模型

對于層數較多的鋼筋混凝土框架和鋼架結構，在地震波的作用下，上層結構的變形以剪切變形為主，為了準確計算出各層的響應情況，可采用多質點計算模型來模擬建筑結構[13].建立多質點模型有三個假定條件：剛性地基，即各點水平運動完全一致；各樓層質量集中在一點；做純剪切運動.具體的模型結構如圖9 所示.

根據達朗貝爾原理，圖9 的隔震模型在地震波作用下的運動方程可表示為[14]：

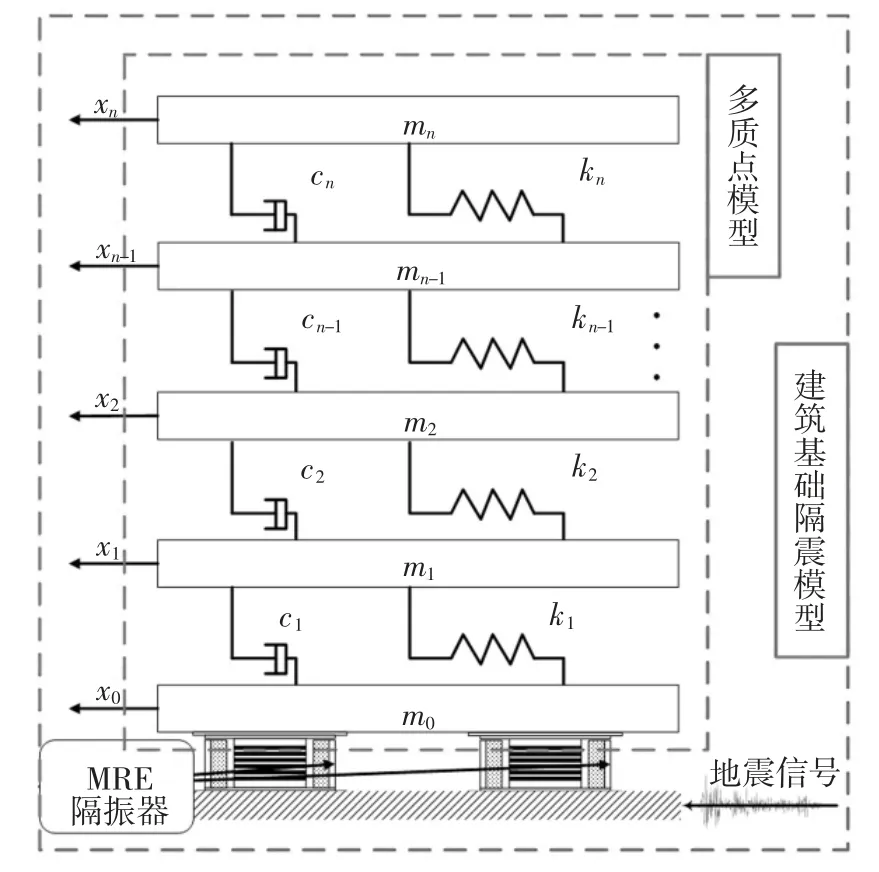
圖9 基礎隔震模型Fig.9 Base isolation model

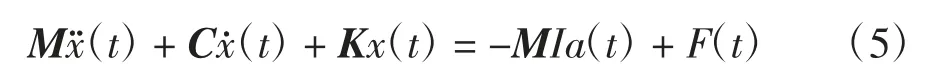
式中：M、K、C 分別為結構的質量、剛度以及阻尼矩陣；x（t）為位移響應；a（t）為地震加速度；F（t）為控制力.I=[1 0 0 …]T1×n.

阻尼采用Rayleigh 阻尼[15]，計算公式如下：

α 和β 為比例系數.

由MRE 隔振器以及電流變化產生的控制力F（t）可表示為：

由式（4）可知：

控制力由隔振器輸出直接作用于建筑的隔震層，可令

式中：m0為隔振層的質量；a0為控制力產生的加速度.

將式（12）代入式（5）可得

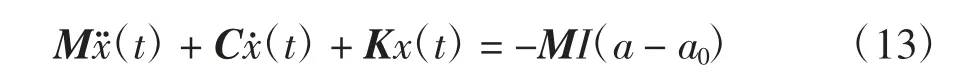
2.2 控制算法

2.2.1 On-off 控制

由表1 可知，隔振器剛度隨電流變化明顯，基于這種特性選用On-off 控制策略進行半主動控制，內容如下[16]：

式中：kmax，kmin為隔振器的最大剛度和最小剛度.當激勵開始時，如果x·≥0，即被控對象偏離并且有偏離更遠的趨勢時，需要增大隔振器的剛度從而抑制這種運動趨勢；當x·＜0 時，被控對象趨近平衡位置，將隔振器剛度調到最小，使其慢慢回歸平衡位置.

2.2.2 模糊控制

模糊控制器包括模糊化、推理機制、模糊規則和解模糊.其中e 作為負載相對位移偏差，是負載位移變化率，e 和作為模糊控制器的輸入，輸出電流I 作為施加在勵磁線圈的電流.輸入論域設置為[-3，3]，輸出論域設置為[-3，3]，將輸入輸出變量劃分為7 個模糊等級.輸入量的隸屬函數選擇Gaussmf 型，可以提升模糊控制的平滑性，輸出量隸屬函數選擇三角型，可以提高控制器的靈敏度，模糊推理機制采用Mamdani 理論，用重心法進行解模糊.模糊規則見表2.

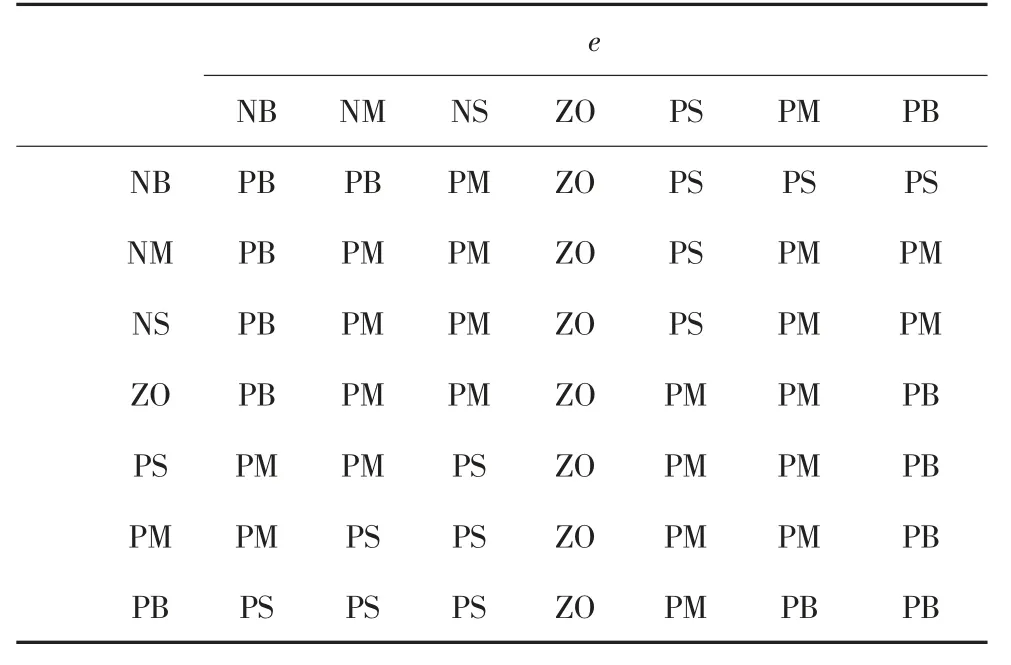
表2 控制規則表Tab.2 Control rule table

2.2.3 遺傳模糊控制

遺傳算法基于自然選擇、適者生存的遺傳思想，具有對問題依賴性小和全局尋優的特點，可應用于模糊控制器的優化.基于上節的模糊控制器，對其隸屬函數進行優化，進而與優化前的模糊控制器控制效果進行比較.

輸入采用的Gaussmf 型隸屬度函數，函數的表達式為：

每一個隸屬函數由兩個參數確定，在雙輸入系統中，每個輸入有7 個模糊子集，所以一共需要優化28 個參數.

考慮到位移是與安全性有關的參數，本文以結構的位移響應作為評價標準，適應度函數為：

遺傳算法的具體參數設置為：種群規模為100，迭代次數為300，交叉概率和變異概率分別為0.9 和0.1.以輸入為EI-Centro 地震波為例，表3 是優化后得到的隸屬度函數參數，圖10 是優化前后隸屬度函數曲線對比，圖11 是優化前后輸入輸出曲面圖對比.從圖11 中可以看出，優化后，當模糊控制器的輸入較大時，可以輸出更大的控制電流，當模糊控制器的輸入較小時，輸出的控制電流可以控制得更小，優化了控制效果.

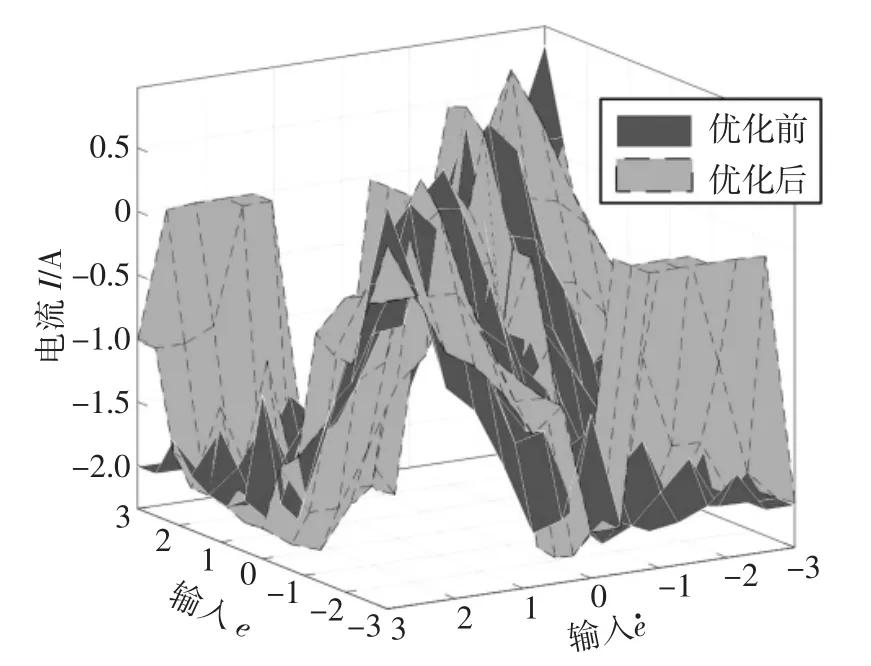
圖11 優化前后輸入輸出曲面圖Fig.11 Input and output surface maps before and after optimization

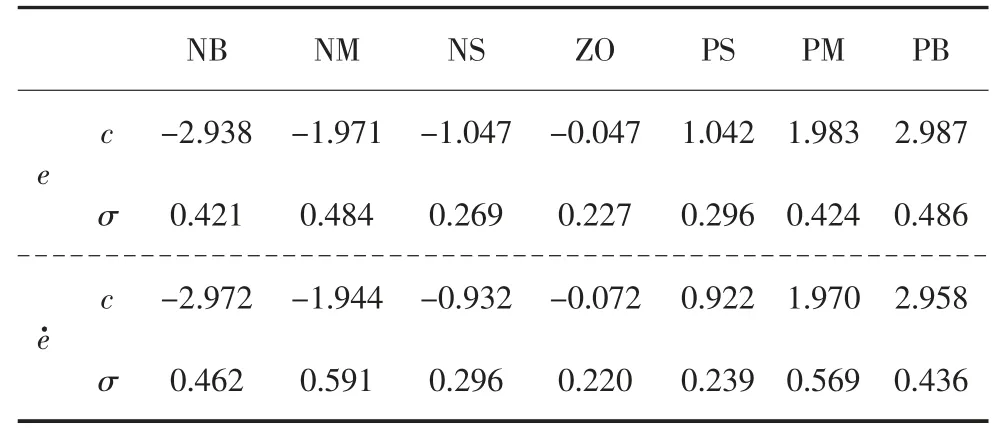
表3 優化后隸屬度參數Tab.3 Membership parameters after optimization

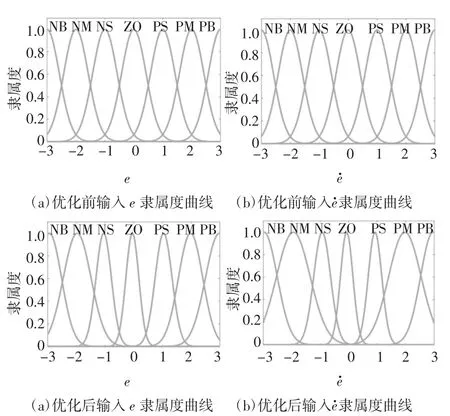
圖10 優化前后隸屬度函數曲線Fig.10 Membership function curve before and after optimization

3 仿真分析

為了驗證MRE 隔振器在變剛度半主動隔振系統中的隔振效果，選取了抗震設防烈度為8 度的某4層商店-住宅砌體結構房屋為例.在EI-Centro 波、Taft 波以及人工地震波的作用下，對其結構進行地震激勵仿真分析，地震波的采樣時間為2 ms，將地震波的加速度幅值設為4 m/s2.建筑結構參數如表4 所示.根據隔振器剛度隨電流變化規律，擬采用20 個MRE 隔振支座，單個支座的剛度為3.4×105kN/m，得到隔震層的總剛度為6.8×105kN/m.根據式（14）系統狀態方程以及圖12 所示的隔振控制系統，可以建立Simulink 模型進行數值仿真分析.

表4 建筑結構參數Tab.4 Building structure parameters

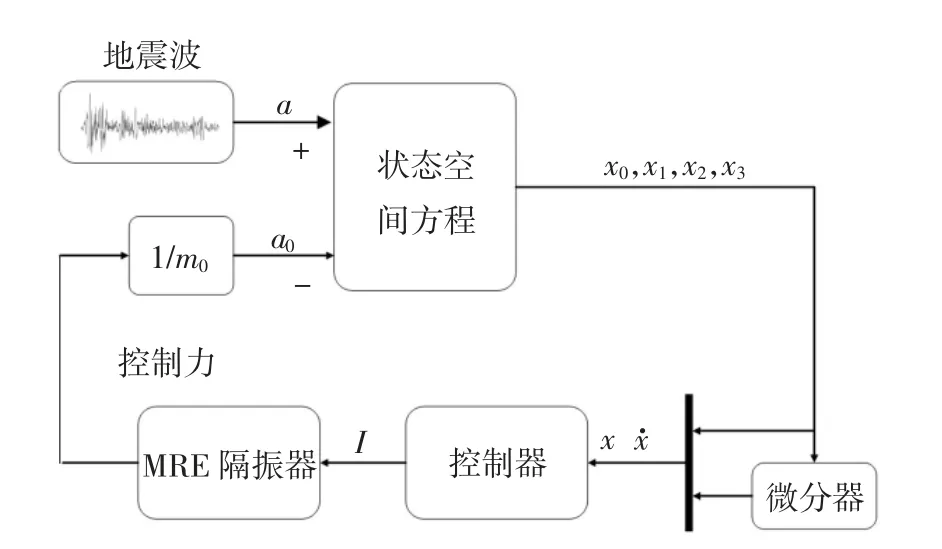
圖12 隔振控制模型Fig.12 Vibration isolation control model

根據圖12 搭建Simulink 動態仿真模型，如圖13 所示.將EI-Centro 波、Taft 波以及人工波三種波作為激勵，嵌入上文提到的On-off 控制、模糊控制以及GA 模糊控制三種控制算法，觀察各自的響應情況.三種地震波的加速度時程曲線如圖14 所示.圖15 為仿真結果，頂層的位移響應時程曲線.

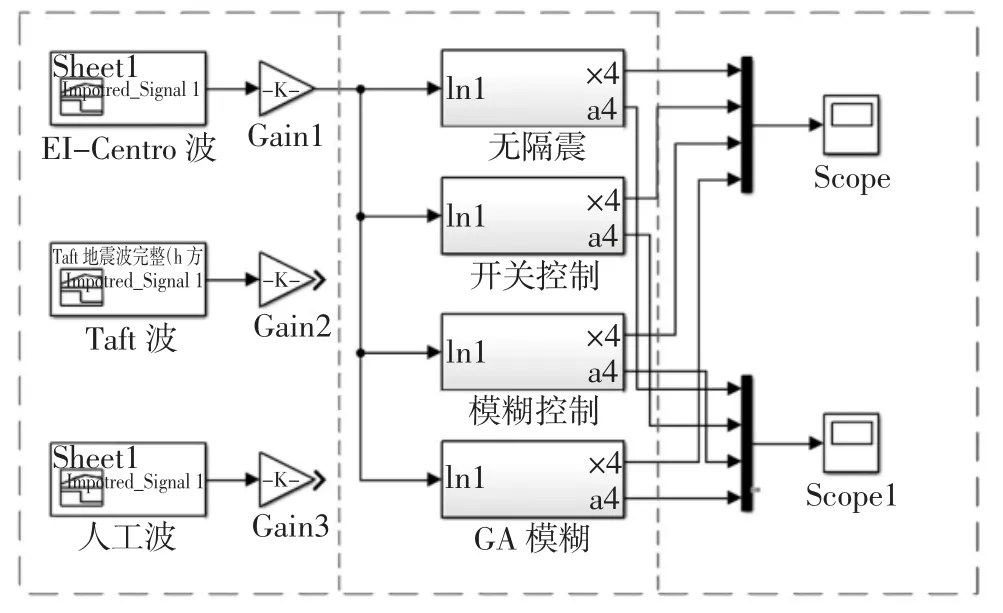
圖13 Simulink 動態仿真模型Fig.13 Simulink dynamic simulation model

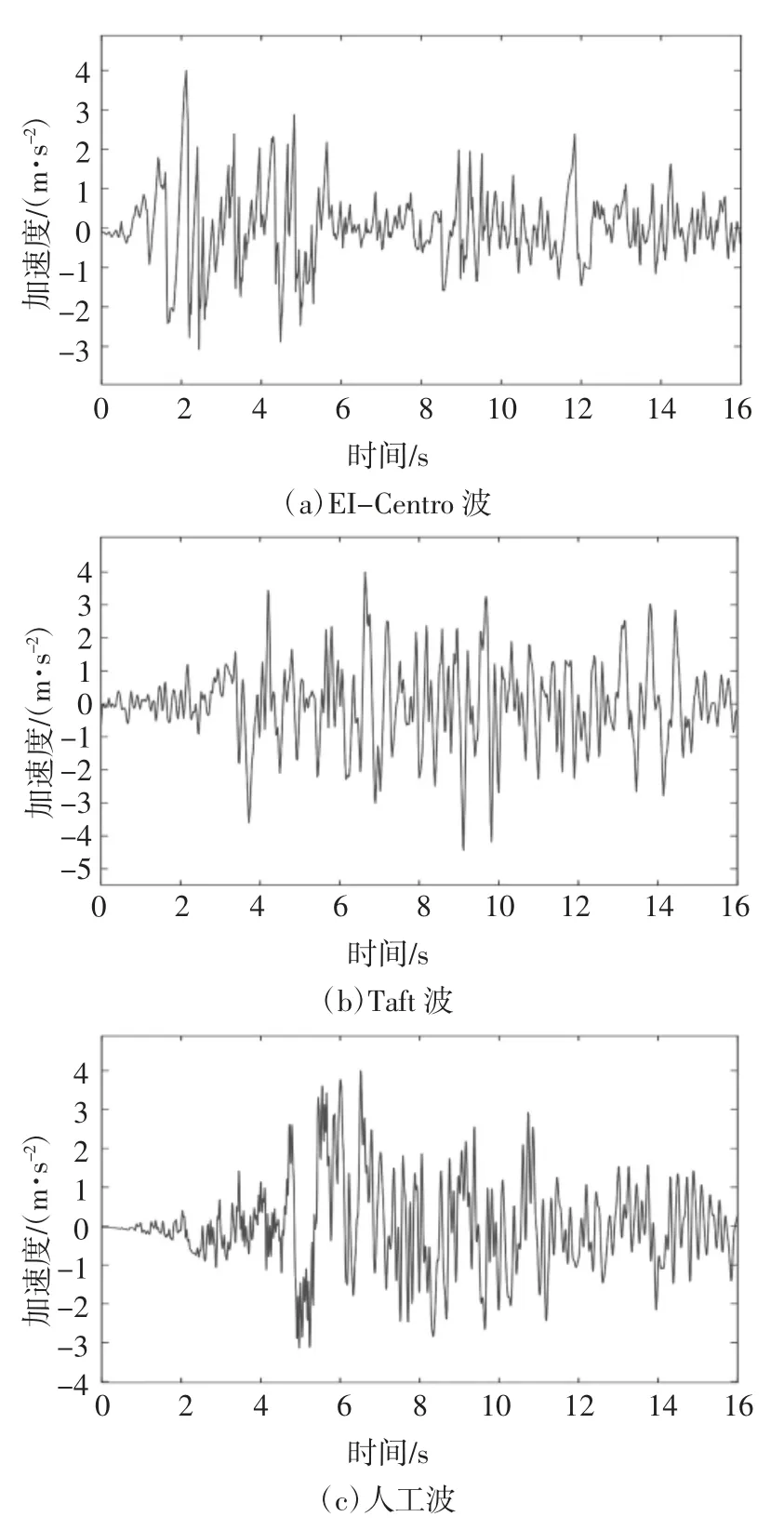
圖14 地震波時程曲線Fig.14 Seismic wave time history curve

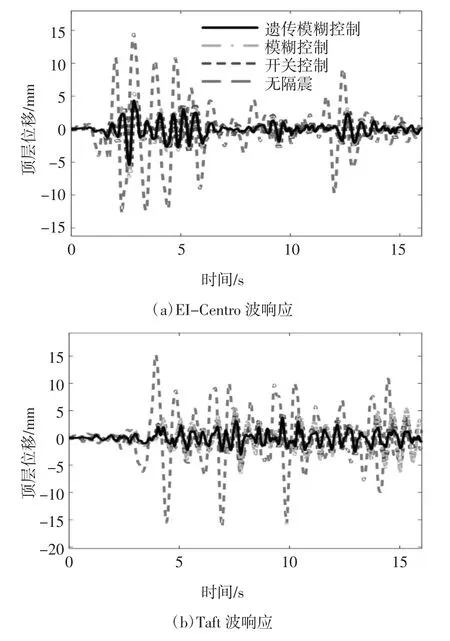
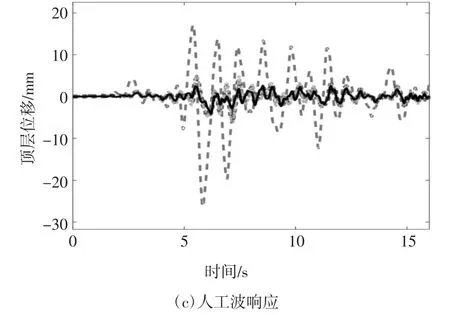
圖15 結構響應時程曲線Fig.15 Time history curve of structural response

從圖15 中可以看出結構在三種控制策略的作用下，頂層的位移響應都具有明顯的下降趨勢，說明了MRE 隔振器可用于對建筑的隔振.通過位移響應對比發現，經過遺傳算法優化的模糊控制器大大提高了控制性能.根據位移響應曲線，提取出各層位移的響應峰值以及位移RMS（Root Mean Square）值得到下表數據.表5、表6 和表7 分別是建筑結構在三種地震波作用下各層位移響應的峰值以及RMS 值，圖16 是位移控制效果對比圖.

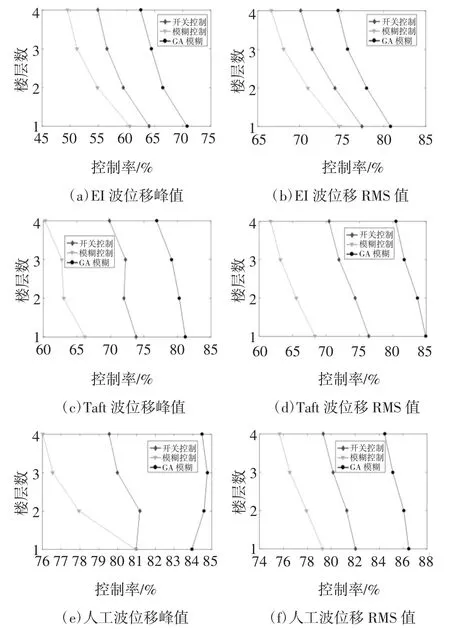
圖16 控制效果對比圖Fig.16 Control effect comparison chart

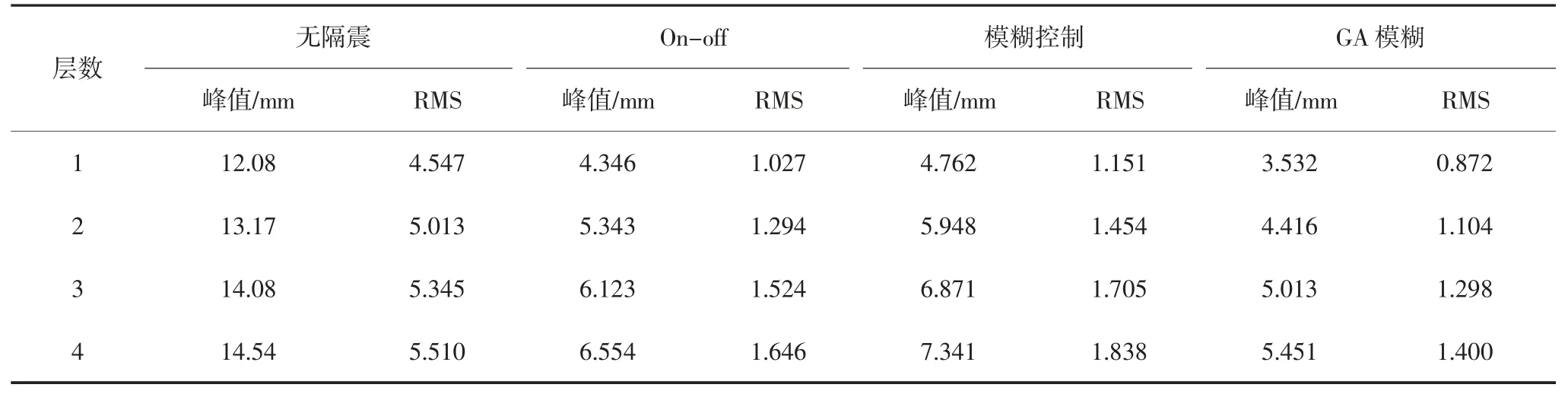
表5 EI-Centro 波作用下結構各層位移峰值及RMS 值Tab.5 Structural displacement peak and RMS under EI-Centro wave

從上圖表中可以看出，三種半主動控制策略對結構的位移響應都具有較好的控制效果，對位移峰值的控制效果達到50%以上，對位移均方根值的控制效果到達了60%以上.對位移均方根的控制效果優于對位移峰值的控制，這說明對激勵過程的整體控制更好.樓層越高，三種控制效果就會越差.三種控制策略對人工波的控制效果最好，對EI-Centro 波的控制效果最差.經過遺傳算法優化后的模糊控制器控制效果改善明顯，提升了10%以上.整體上Onoff 控制優于模糊控制，但是On-off 控制在工作時是持續輸出最大電流，相比較而言，模糊控制可以節省更多的能源，GA 模糊控制在輸出電流方面更加合理，控制效果更好，在實際工程中有應用的潛力.

4 結論

1）自行制備的MRE 在外部磁感應強度逐漸增大的條件下，儲能模量顯著增大，磁流變效應達到2 000%以上.設計制作的磁流變彈性體隔振器變剛度特性明顯，適用于變剛度半主動隔振控制系統.

2）以某4 層鋼筋混凝土建筑為例，采用On-off控制、模糊控制以及GA 模糊控制算法進行控制效果的比較分析，驗證了磁流變彈性體隔振器應用于變剛度半主動隔振控制系統的有效性.

3）三種半主動控制策略都具有良好的控制效果，對位移峰值的控制都能達到50%以上，對位移均方根值的控制更好，能達到60%以上.

4）運用遺傳優化算法對模糊控制器的參數進行優化，優化后的模糊控制器在控制輸出方面的性能有了一定的提升，整體的控制效果提升明顯，超過了10%.