基于T-SSA算法的流水車間訂單調度問題研究
王 婷,毋 濤
(西安工程大學 計算機科學學院,陜西 西安 710048)
0 引 言
隨著中國經濟社會的發展,產品定制服務的出現,消費者個性化需求也日益凸顯,有一部分制造型企業開始采用訂單生產模式[1](make-to-order,MTO),比如西裝定制、船舶制造。
在MTO生產模式中,訂單內不同的工件的交貨期不同,而制造型企業通常都是配備固定的車間、機器和人員,訂單調度決策往往受車間生產能力的制約。在這種情況下,這種決策往往會與實際生產有所偏差,造成計劃外的生產成本(如加班、外包)和拖期罰金,導致企業信譽受損,客戶滿意度降低。
為提高訂單交付的準時率,企業需要在有限產能下對訂單生產作業進行合理的計劃安排和調度,依據訂單產品的要求交期及時交付產品,履行合約。研究基于流水線車間的訂單調度問題可以有效提高企業的生產效率和競爭力,對于處于MTO生產模式的企業制定出合理有效的訂單調度決策,及時交付作業具有重要的研究意義。
長期以來,混合流水車間調度問題[2](hybrid flow shop scheduling problem,HFSP)被證明是一個經典的NP難題。目前,求解HFSP的算法主要包括遍歷式算法、構造型算法和智能化優化算法,其中遍歷式算法可以求解出該類問題的精確解,但計算速度較慢;構造型算法在求解該類問題時運算速度較快,但算法結構復雜且通常無法求解出全局最優解[3];優化算法有嚴格的理論基礎,能在短時間內解決問題的最優或理想解。智能優化算法[4]主要有混合螢火蟲算法(hybrid firefly algorithms,HFA)[5]、最佳覓食算法(optimal foraging algorithm,OFA)[6]、離散狼群算法(discrete wolf pack algorithm,DWPA)[7]、離散布谷鳥算法(cuckoo search,CS)[8]、改進蛙跳算法(shuffled frog leaping algorithm,SFLA)[9]、果蠅優化算法(fruit fly optimization algorithm,FOA)[10]、混合魚群算法(hybrid artificial fish swarm algorithm,HAFSA)[11]、人工蜂群算法(artificial bee colony algorithm,ABC)[12]等等,已經廣泛應用于解決各種生產調度問題。
麻雀搜索算法[13](sparrow search algorithm,SSA)是一種新型的群智能優化算法,主要是受麻雀的覓食行為和反捕食行為的啟發。針對SSA的研究表明,該算法在不同的搜索空間中具有良好的性能。在SSA的基礎上,文中提出了基于生產環節生產線兩段式麻雀搜索算法(two-vector sparrow search algorithm,T-SSA),并將T-SSA實際應用于流水車間訂單調度問題中,驗證了該算法的有效性。
1 問題描述與建模
1.1 問題描述
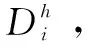
1.2 模型的假設條件
(1)在初始時間(設置為0),可以處理任何訂單任務。
(2)同一生產線的同一時間只能加工1件產品。
(3)不同的訂單任務之間沒有先后約束。
(4)在生產過程中,訂單前一個生產環節被處理完成后,會立即進入下一個生產環節進行處理;如果下一個生產環節生產線正在工作,則訂單進行等待。
(5)每兩個處理環節之間有足夠的緩存空間,允許產品在處理環節之間停留和等待。
(6)訂單調度過程為非搶占式調度。
(7)訂單任務中各生產環節的交貨時間和利潤值均為已知量(交貨時間從初始時間0開始計算)。
根據上述解釋和假設,研究的問題是:確定訂單的加工順序和各生產環節的生產線分配,從而使加權訂單完成時間最小化。
1.3 參數和變量說明
i:表示待加工工件編號。
j:表示待加工的生產環節序號。
k:表示每個生產環節的生產線編號。
Mj:第j個生產環節并行生產線的集合。
NMj:第j個生產環節并行生產線的數量。
MPij:工件i在第j個生產環節可用的生產線集合,MPij?Mj。
tijk:工件i的第j個生產環節在生產線k上的加工時間。
stijk:工件i的第j個生產環節在生產線k上的開始加工時間。
etijk:工件i的第j個生產環節在生產線k上的結束加工時間。
xijk:當工件i的第j個生產環節在生產線k上的加工時xijk=1;否則xijk=0。
rjk:第j個生產環節在生產線k上加工的第r個任務的工件編號。
Ti:工件i的各生產環節加工時間總和。
1.4 模型構建
根據問題描述,采用最小最大訂單完成時間為目標函數,可轉化為求解訂單內工件集的最小化完成時間,即一個工件完成時間的最小值,模型構建具體如下:
(1)
模型描述如下:
etijk≤sti(j+1)k*;i=1,2,…,n;j=1,2,…,s;
k∈MPij;k*∈MPi(j+1)
(2)
etijk=stijk+tijk;i=1,2,…,n;j=1,2,…,s;
k∈MPij
(3)
(4)
r=1,2,…,Njk-1
(5)
若rjk=i,則:
其中:
k∈MPij,k-∈MPi(j-1),r=1,2,…,Njk
(6)
(7)
xijk∈{0,1},xijk-=1,?i,j,k,r
(8)
(9)
公式(1)是最小化工件完成時間的公式和目標函數;公式(2)表示在前一個生產環節完成后,才可以在下一個生產環節中進行加工;公式(3)表示每個工件的加工完成時間,其中每個生產環節的加工結束完成時間取決于該生產環節的開始時間和加工時長;公式(4)表示工件的每個生產環節只能選擇該生產環節的一臺生產線進行加工;公式(5)表示一條生產線同時只能加工一個工件;公式(6)表示當工件i是第j個生產環節在生產線k上處理的第r個任務時,生產環節開始時間取決于該工件前一個生產環節的結束時間與本生產線的前一任務結束時間;公式(7)表示每個工件的完成時間等于工件在最后一個生產環節中的完成時間;公式(8)為變量取值范圍;公式(9)表示每個工件每個生產環節加工時間的計算關系,即工件的總加工時間。
2 麻雀搜索算法(SSA)
麻雀搜索算法是一種基于麻雀覓食行為和反捕食行為的新型群體智能優化算法,其仿生原理如下:
在麻雀覓食的過程中,將整個麻雀種群分為發現者和加入者兩種角色,疊加了偵查預警機制。發現者在種群中負責尋找食物并為整個麻雀種群提供覓食區域和方向,而加入者則是利用發現者來獲取食物。為了獲得食物,麻雀通常可以采用發現者和加入者這兩種行為策略進行覓食。種群中的個體會監視群體中其他個體的行為,并且該種群中的攻擊者會與高攝取量的同伴爭奪食物資源,以提高自己的捕食率。此外,當麻雀種群受到捕食者的攻擊時會做出反捕食行為。
SSA算法的具體流程見圖1。
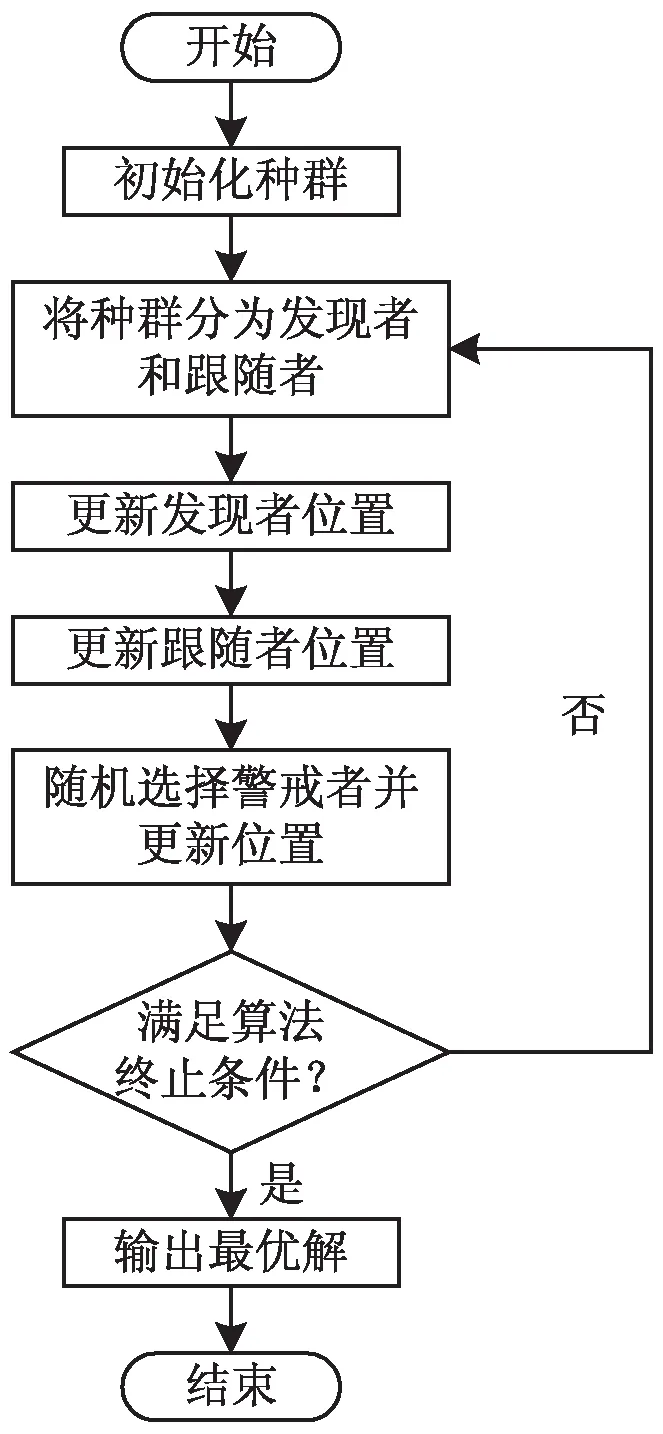
圖1 麻雀搜索算法流程
Step1:初始化麻雀種群。
Step2:設置發現者規模,將種群分為發現者和跟隨者。
Step3:(發現者位置更新)當預警值小于安全值的時候,即覓食環境沒有捕食者時,發現者位置隨機更新;若預警值大于安全值,種群中的一些麻雀已經發現了捕食者,并向種群中其他麻雀發出了警報,此時所有麻雀都需要迅速飛到其他安全的地方進行覓食。更新方式如公式(10):
(10)
上式表示種群中第t代中的第i個個體的第j維位置信息,α和Q是服從不同分布的隨機數。itermax、R2、ST分別表示最大迭代次數、預警值和安全值。
Step4:(跟隨者位置更新)若當前跟隨者處于十分饑餓的狀態,則需要飛往其他地方覓食,以獲得更多的能量,進行位置更新;否則,跟隨者是圍繞最好的發現者周圍進行覓食,期間也有可能發生食物爭奪,使自己成為生產者。更新方式如公式(11):
(11)
其中,Xp是目前發現者的最優位置,Xworst是當前全局最差的位置,n是種群大小。
Step5:(隨機選擇警戒者并更新位置)當任意麻雀意識到危險靠近時,它們會放棄當前的食物,即無論該麻雀是發現者還是跟隨者,都將放棄當前的食物而移動到一個新的位置,處于種群外圍的麻雀向安全區域靠攏,處于種群中心的麻雀則隨機行走靠近別的麻雀。更新規則如公式(12):
(12)
其中,Xbest是當前的全局最優位置,fg和fw分別是當前全局最佳和最差的適應度值,fi是當前麻雀的適應度值,ε、β、K是不同隨機常數。
Step6:判斷是否達到最大迭代次數,若達到,則輸出最優適應度值,即所求問題的最優解,否則轉到Step2。
3 基于T-SSA算法的模型求解
針對流水車間訂單調度問題采用基于生產環節和生產線的兩段式編碼方式來表示麻雀種群中麻雀的位置。應用其設計的初始化種群方式初始化種群,對麻雀的智能行為進行重新設計;則基于兩段式麻雀搜索算法的流水車間訂單調度問題的具體操作如下:
3.1 編碼方式
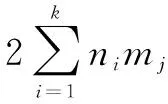
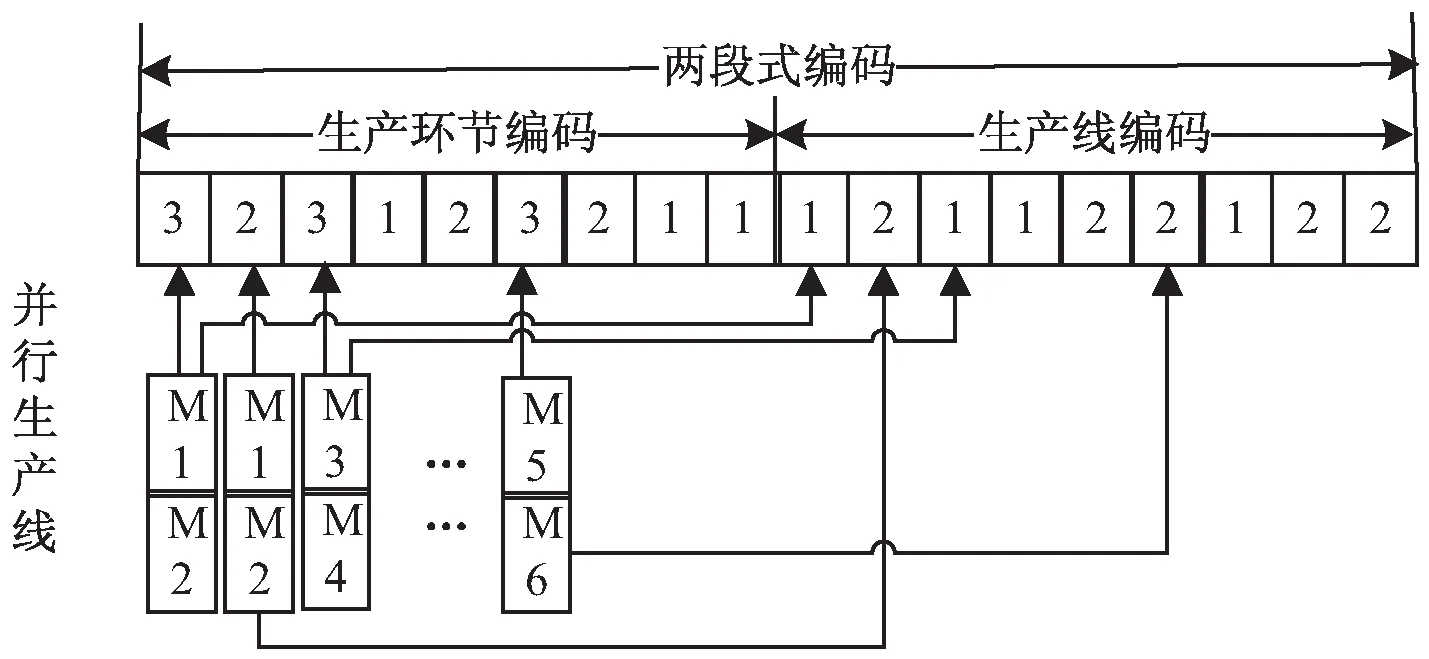
圖2 兩段式編碼示意圖
生產環節編碼的編碼長度為總生產環節數,基因位上的數字表示工件號,相同工件號出現的次數對應工件的第幾個生產環節。圖2中表示的工件加工順序為:工件3→工件2→工件3→工件1→工件2→工件3→工件2→工件1→工件1,其中每個工件出現三次,即每個工件有3個生產環節,比如基因位1上的數字3,表示工件3的第一個生產環節,基因位3上的數字3,表示工件3的第二個生產環節,諸如此類。
生產線編碼的編碼長度與生產環節編碼長度一致,也是總生產環節數,基因位上的數字代表前半段對應的生產環節可以選擇的生產線集合中的第幾條生產線。圖2中表示選擇的生產線順序依次為:生產線M1→生產線M2→生產線M3→生產線M1→生產線M4→生產線M6→生產線M5→生產線M4→生產線M6,基因位10位上的數字1表示工件3的第一個生產環節選擇生產線M1加工,基因位12上的數字1表示工件3的第二個生產環節上選擇生產線M3加工,以此類推。
[3,2,3,1,2,3,2,1,1,1,2,1,1,2,2,1,2,2]整個整數段表示一只麻雀個體。
3.2 種群初始化
在麻雀搜索算法中,多樣性好的初始解集能夠有效提高運算效率,擴大搜索范圍,避免局部收斂的情況發生。考慮到兩段式編碼的特點,先采用隨機初始化方式產生足夠多的麻雀個體,確保種群的多樣性,然后使用輪盤賭選擇機制選取所需數量的初始個體,確保種群的質量。采用權重法計算個體被選取的概率,優先選擇收益高、交期緊、訂單權重大的工件個體,工件選擇概率越大,個體越容易被選用。
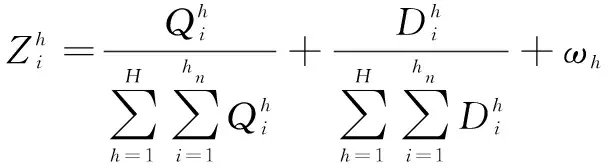
(13)
(14)
3.3 適應度函數
以最小化最大訂單完成時間為目標函數求解流水車間訂單調度問題,主要思想是訂單內的每個工件的完成時間最優,可以將該問題轉化為求解訂單內工件集的最小化最大完成時間為適應度函數,工件最大完成時間越小,表示個體的適應度值越好,即fitness=min{Cmax(P)}。
3.4 智能行為設計
文中以最小化最大訂單完工時間為目標函數來確定最優訂單調度方案,即訂單中工件的生產環節排序和生產線選擇方案。結合HFSP的特性,對兩段式麻雀搜索算法中的具體定義如下:
(1)最優最差麻雀選擇機制。
記錄第i只麻雀個體的適應度函數為Fiti,根據適應度值對麻雀個體進行排序,那么取全局最差適應度值為worseF=max(Fiti),i=1,2,…,n,worseF對應的全局最差位置為worseX;最優麻雀個體對應的適應度值為bestF1=min(Fiti),i=1,2,…,nbestF1對應的全局最優位置為bestX1。
(2)發現者移動機制。
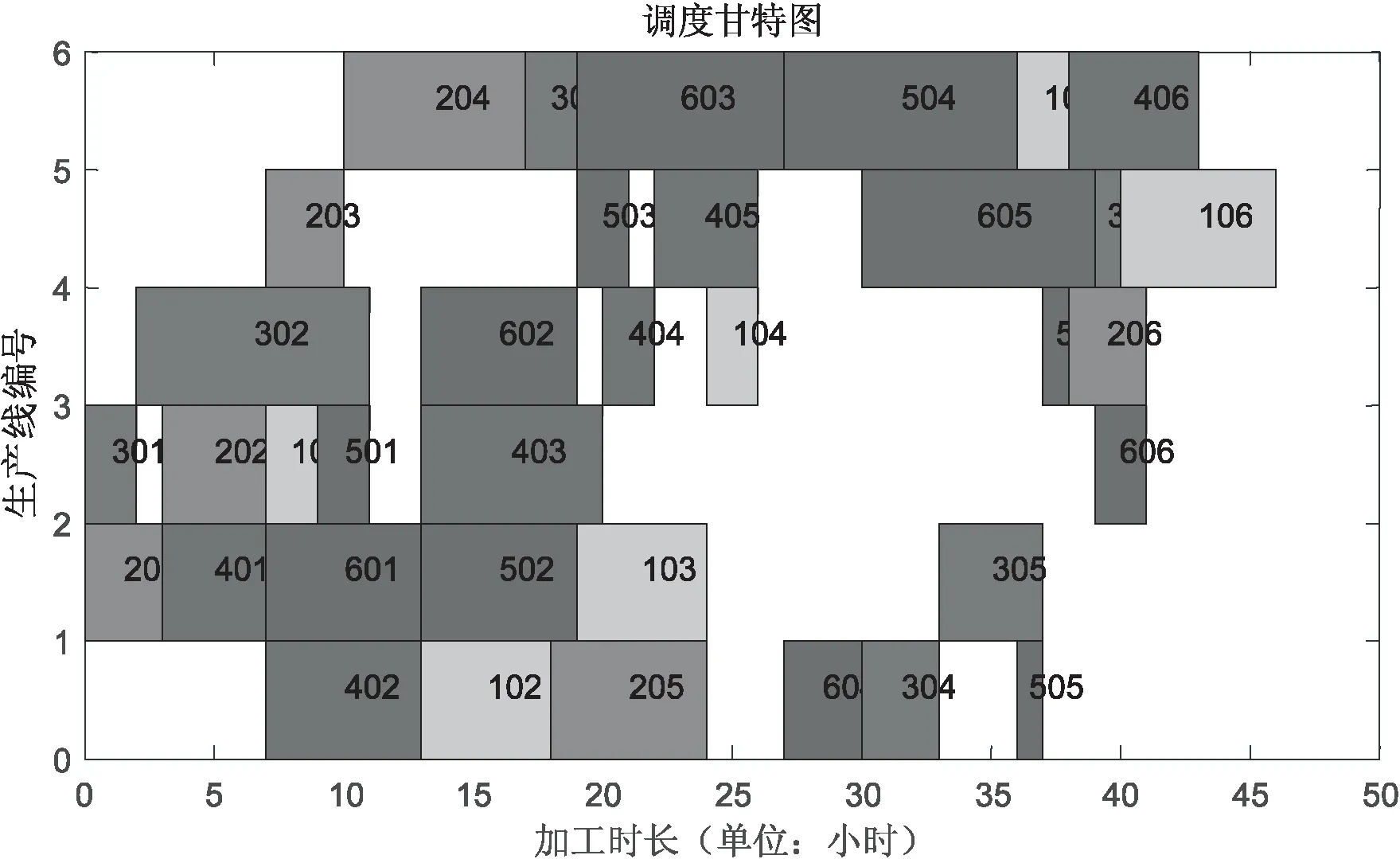
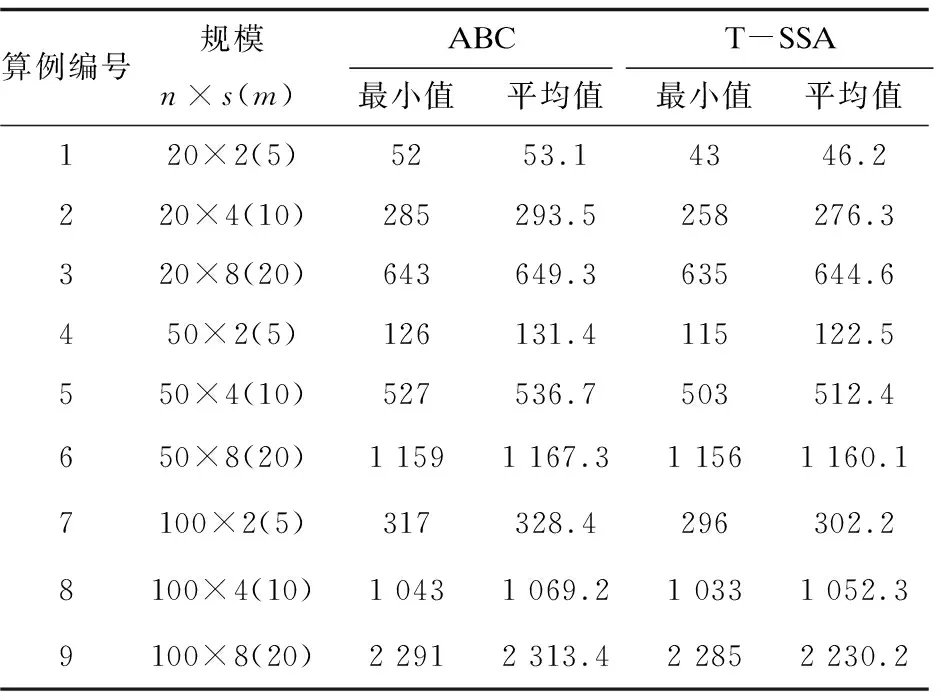
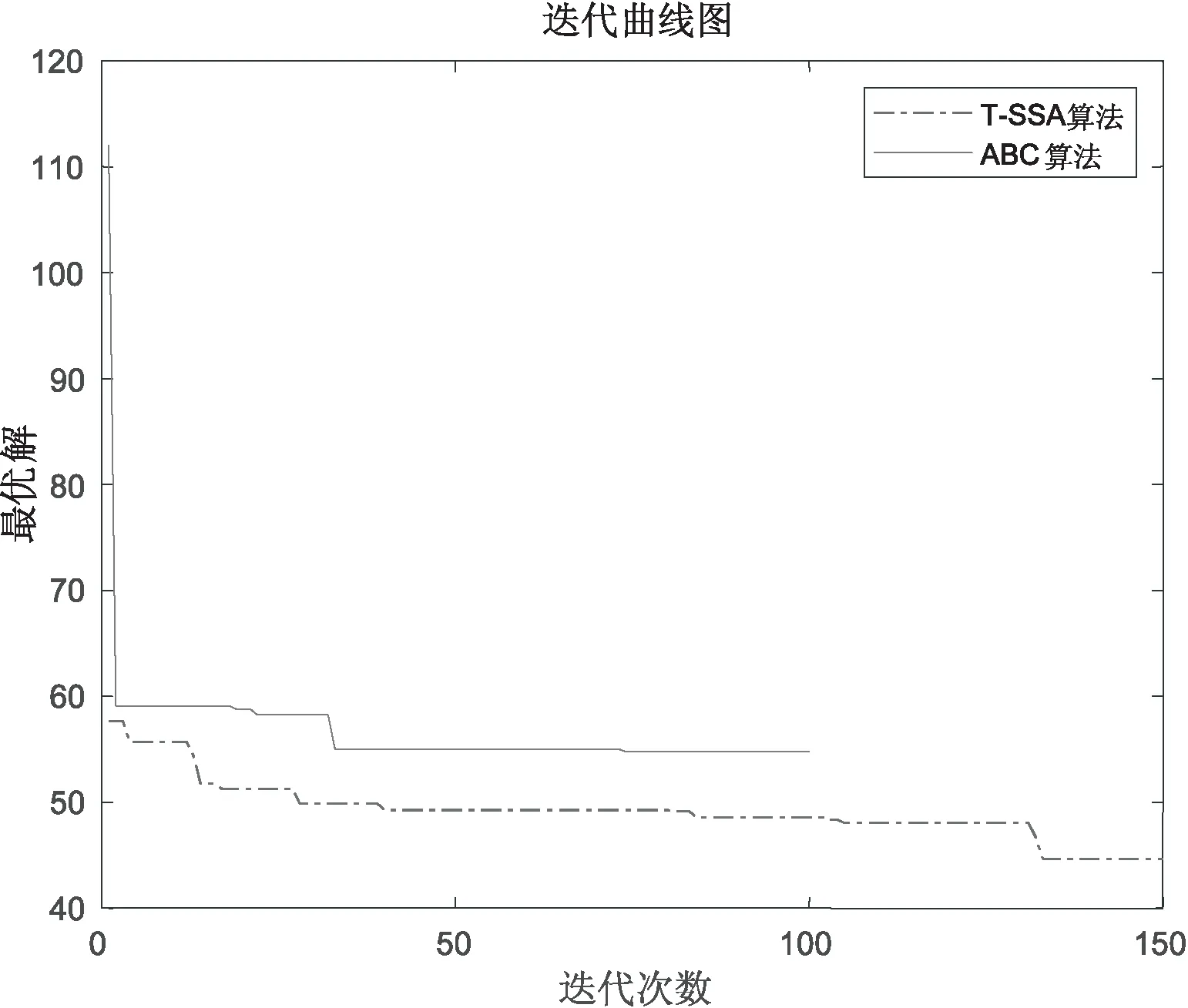
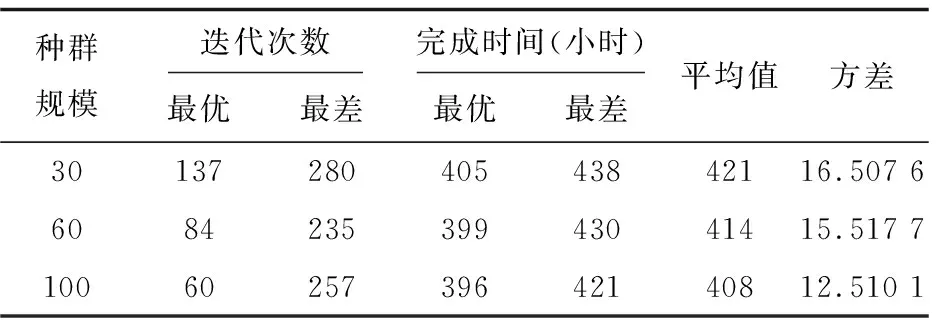
根據設置麻雀發現者個體的比例PR,從種群中隨機取出發現者的個體數量。將隨機預警值R2與發現者警戒閾值ST進行比較,若R2 (3)跟隨者跟隨機制。 (4)偵察預警機制(警戒者)。 對意識到危險的個體稱為警戒者,并不代表出現了真正的捕食者。隨機指定個體j,取該個體的適應度值為Fitj,若Fitj>bestX1,表示此時的麻雀正處于種群的邊緣,極其容易受到捕食者的攻擊,位置跳躍性比較大,警戒者位置更新;若Fitj=bestX1,表明處于種群中間的麻雀意識到了危險,需要靠近其他的麻雀以此盡量減少它們被捕食的風險。 根據智能行為設計的4大機制,可將使用T-SSA算法求解流水車間訂單調度問題的步驟概括如下: Step1:初始化算法相關參數。設置種群的規模大小為pop,最大迭代次數為itermax,發現者比例為PR,偵查者比例為SD,預警值為R2,發現者警戒閾值為ST。 Step2:根據初始化方案進行種群初始化,確定麻雀個體的位置編碼。 Step3:依據設定的PR,將種群分為發現者和跟隨者。計算個體的適應度值Fiti,進行排序,并取出種群最優位置bestX1和最差位置worseF對應的適應度值bestF1、worseF。 Step4:將預警值R2與警戒閾值進行比較,更新所有發現者位置,淘汰掉邊緣個體,迭代并計算發現者的適應度值。取出發現者的最優位置bestX2對應的適應度值bestF2。 Step5:依據跟隨者的編號,判斷跟隨者的狀態,淘汰邊緣個體,跟隨者進行隨機位置更換,或者搶奪最優發現者bestX2成為發現者。迭代,計算所有跟隨者的適應度值。 Step6:判斷隨機警戒者所處位置是否在種群中心,若處在中心,向最差位置worseF個體移動位置,淘汰邊界個體,更新警戒者的適應度值。 Step7:求解最新全局個體適應度值,替換最優位置bestX1及其響應的適應度值bestF1。 Step8:判斷是否達到最大迭代次數,若達到,則輸出最優適應度值,即所求問題的最優解,否則轉到Step4。 實驗仿真環境為操作系統Windows8、處理器Intel(R) Core(TM)i5-4210U CPU @ 1.70 GHz 2.40 GHz、內存12G,采用Matlab R2018a。 采用以下兩種方式驗證算法的有效性: (1)實例驗證一。 圖3 TSSA算法測試甘特圖 由圖可知,兩段式麻雀搜索算法甘特圖調度結果顯示46小時可完成6個工件的生產,與文獻[13]中優化的SA-PSO-GA調度效果相同,均優于傳統的PSO-GA算法。將T-SSA算法的迭代曲線與原文獻比較,PSO-GA算法和SA-PSO-GA更易陷入局部最優,輸出的解并非實際最優解。從運行時間上來看,由于T-SSA達到最優的迭代次數較少,運算時間為14-17S,在效率上明顯高于原文中提到的算法。 (2)實例驗證二。 設置9種不同規模的調度算例,隨機生成訂單數量、訂單權重、訂單收益,訂單中的工件數量合計分別為20、50、100,生產環節數為2、4、8,生產線條數分別合計為5、10、20,工件交期根據EDD規則[15]與經驗設置。數據結果與4.2中的數據格式類似。對生成的訂單數據進行處理,得到算例規模n×s(m),n表示工件數,s表示生產環節數,m表示生產線總數。 使用相同的算法參數和編碼方式對人工蜂群算法(ABC)[12]、兩段式麻雀搜索算法(T-SSA)進行9次實例驗證比較。仿真結果如表1所示,在不同規模的算例中,T-SSA求解的最小值、平均值基本優于ABC算法,體現出了明顯的搜索能力。 表1 實例運行結果統計(最小值、平均值單位:小時) 其中某一次的迭代曲線如圖4所示,實驗結果基本類似,ABC的最優解T-SSA均可在相近迭代次數到達,且最優解的消耗時長接近。結合表1和圖5可以看出,T-SSA的最優解質量更好,表明該算法的搜索能力更強,更進一步證明了該算法的有效性和優越性。 圖4 訂單調度迭代圖 結合上海某西裝定制企業的流水車間生產過程為實例作為研究對象,驗證訂單調度模型和兩段式麻雀算法的有效性。該生產企業的西裝定制生產過程可描述為有限并行生產線混合流水車間,所有西裝定制產品從加工到結束,主要分為五個環節:裁剪有2條生產線(M1,M2);縫制有3條生產線(M3,M4,M5)、手縫有3條生產線(M6,M7,M8)、整燙有2條生產線(M9,M10),檢驗有2條生產線(M11,M12)。此處忽略不同工件的規格、生產工藝在每個加工環節的局部差異。本次選取該企業一次實際生產任務為實驗對象,共有8個客戶訂單,合計20個待加工工件,訂單權重、交貨期、工件收益已知。假設所有訂單在0時刻接受,且所有生產線環境運作正常,物料庫存充足。模擬訂單信息數據如表2所示,表3為訂單對應的西裝企業生產工時數據。 表2 訂單信息 表3 上海某西裝定制企業生產工時(單位:小時) 使用T-SSA算法進行實例調度,設置種群數量分別為30、60、100,最大迭代次數為500,發現者警戒閾值為0.8,發現者比例為20%,重復多次計算以上訂單實例。 續表3 各種群規模隨機取20次運算結果統計如表4所示,最優迭代次數均在150代以內,運算時間較短。實際結果表明,種群增大可以有效減少迭代次數,得到目標值。 表4 實例運行結果統計 目前該企業還是通過傳統的Excel和人為經驗制作訂單生產排程,人工負荷調整工作量巨大,采用這種方式進行以上實例調度編排企業應用總共耗時450分鐘,使用T-SSA算法運行實例,最差結果也是少于450分鐘的,驗證了兩段式麻雀搜索算法結果流水車間訂單調度問題的實用性和有效性。 針對流水車間訂單調度問題,建立單目標數學模型,采用兩段式雙層編碼的麻雀搜索算法進行問題求解,對發現者、跟隨者、警戒者三種角色采用不同的機制更新策略。算法很好地挖掘了全局最優潛在區域的能力,從而有效地避免了局部最優問題。將T-SSA算法與文獻[10,12]中的算法進行模擬比較,驗證了算法的有效性和優越性。采用企業訂單調度實例測試T-SSA,更近一步驗證了T-SSA的有效性和實用性。不足之處是,T-SSA在求解大規模應用時,耗時稍微長一些,可對算法進行進一步的研究,將其擴展使用在更復雜的調度問題中,例如多目標調度問題。
3.5 T-SSA算法迭代過程
4 算法驗證與分析
4.1 算法仿真驗證
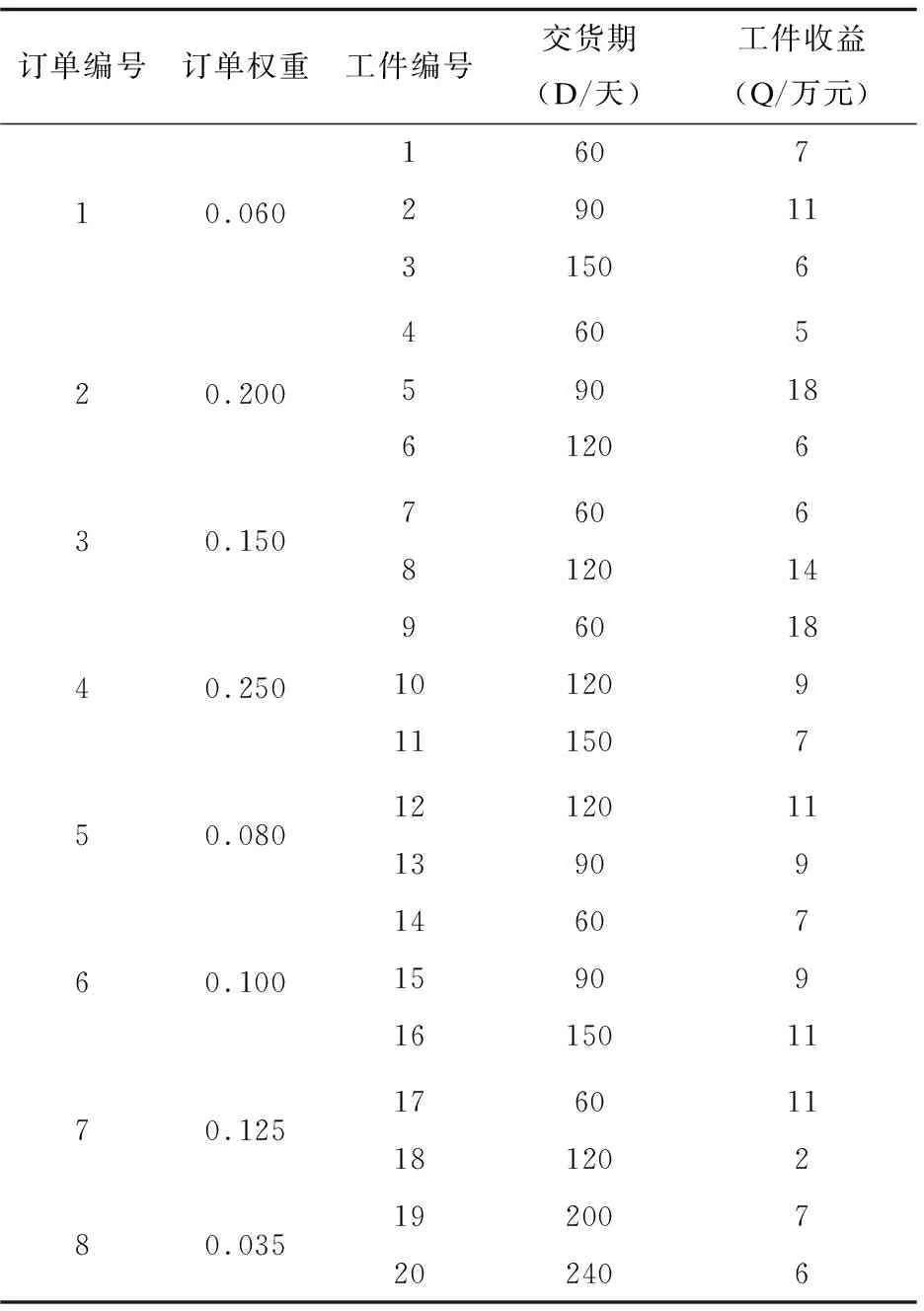
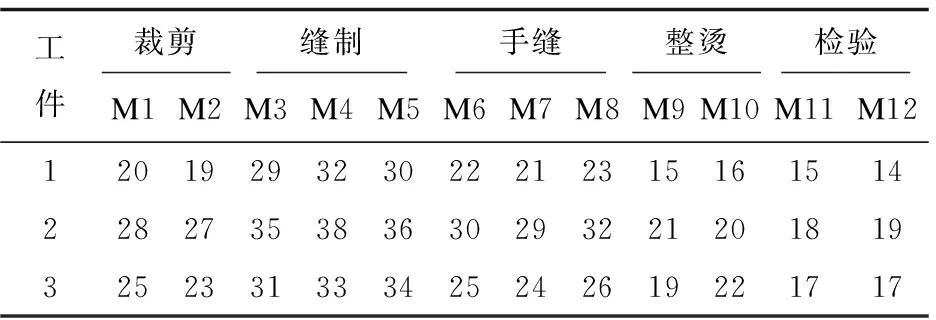
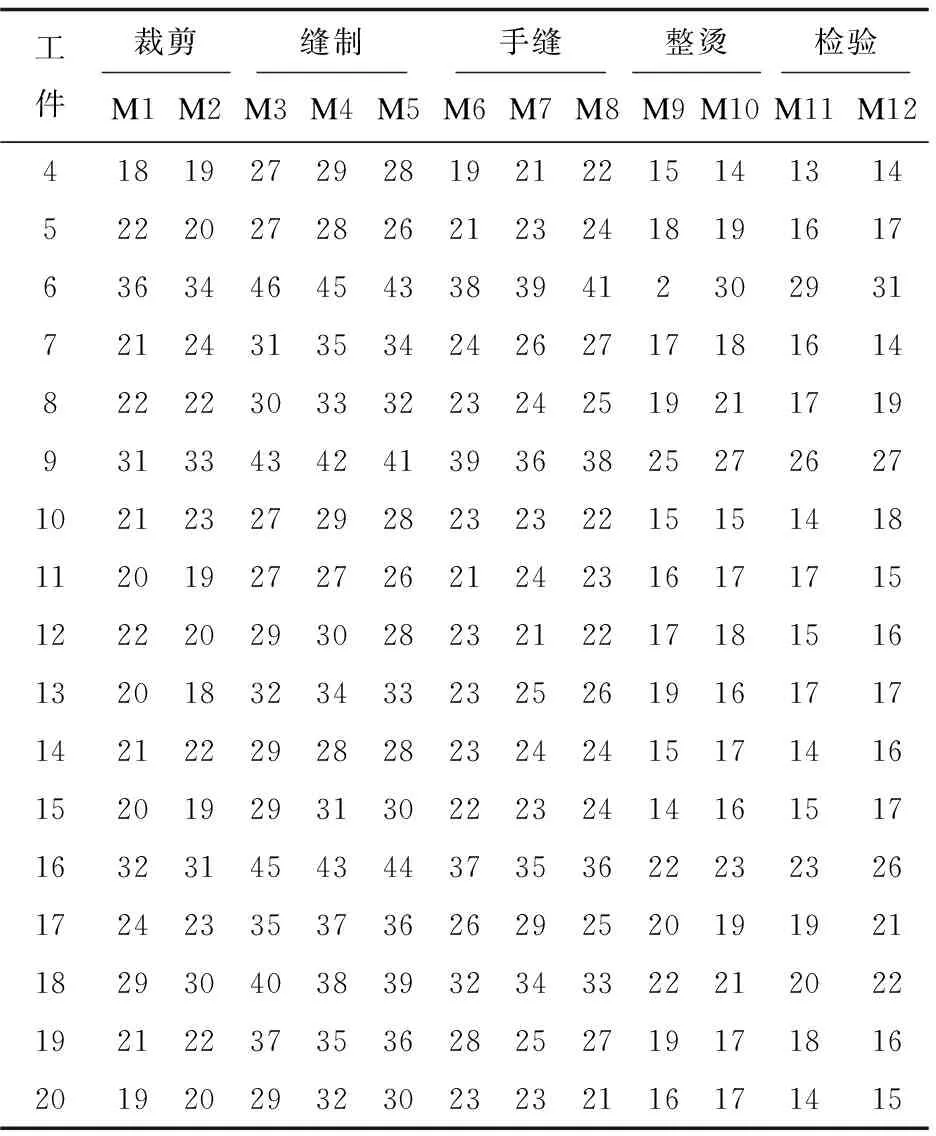
4.2 訂單調度實例應用驗證
5 結束語

