六自由度機械臂運動學旋量逆解及簡化算法*

劉國平，楊先永，鐘飛飛，王大海

(南昌大學機電工程學院，南昌 330031)

0 引言

機器人的運動學是機器人控制的基礎，其包括正運動學和逆運動學兩個部分；當前國內(nèi)外運動學研究主要采用D-H參數(shù)法和旋量法[1-2]。相比于傳統(tǒng)的D-H參數(shù)法，旋量法具有不需要建立局部坐標系因此避開了局部坐標系帶來的奇異性問題，并且能夠很好的區(qū)分多解和具有明顯的幾何意義等優(yōu)點[3-5]，所以越來越多的學者將旋量引用到機器人的研究中。

文獻[6]將paden-kahan子問題和消元法相結(jié)合解決了后3關節(jié)交于一點的六自由度逆解問題。文獻[7]將吳方法(吳方法是我國數(shù)學家吳文俊于20世紀70年代提出的處理多項式代數(shù)問題的一種數(shù)學方法)引入6R機器人的逆運動學問題中來，解決旋量算法子問題的限制。文獻[8]將希爾維斯特(sylvester)結(jié)式法與旋量理論相結(jié)合來求取6自由度機器人的逆解，擺脫了對paden-kahan子問題的依賴性。文獻[9]針對前3關節(jié)軸線均不相交，后3關節(jié)相交于一點的六自由度機器人，提出了幾何法和旋量法相結(jié)合的運動學逆解求解算法。文獻[10]針對前3關節(jié)不相交，后3關節(jié)相交構型的“錢江一號”機器人提出了一種新的運動學逆解子問題算法。文獻[11]針對工業(yè)機器人提出了一類子問題，并以IRB1400弧焊機器人為例驗證算法的正確性。文獻[12]提出了新的旋量子問題改進一類前3關節(jié)均不相交的六自由度運動學逆解求解方法。

綜合上述文獻，當前旋量理論在逆運動學求解上的研究還存在以下問題：①多數(shù)研究主要針對后3關節(jié)交于一點構型的六自由度機械臂，缺少旋量理論解決前3關節(jié)交于一點的六自由度機械臂逆解研究。②僅僅依靠傳統(tǒng)的旋量理論和panden-kahan子問題來求取逆解，其過程和結(jié)果還不夠簡潔。

本文針對前3關節(jié)交于一點的六自由度機械臂提出一種旋量逆解算法，并采用幾何法及歐拉角對算法進行簡化改進。

1 基于旋量理論的運動學模型

1.1 旋量描述剛體運動

歐拉定理說明，任何一個剛體的旋轉(zhuǎn)運動都可以用一個旋轉(zhuǎn)矩陣R來描述，該旋轉(zhuǎn)矩陣R可以表示成轉(zhuǎn)角θ和轉(zhuǎn)軸的單位矢量ω的函數(shù)：

(1)

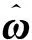
(2)

根據(jù)Chasles定理，任何剛體運動都可以拆分為沿著某直線的移動和旋轉(zhuǎn)來表示，可以用如下的指數(shù)積形式來表示。

(3)

當工具坐標系{T}相對于參考坐標系{S}的初始位形為gST(0)時，繞某軸螺旋運動的剛體，{T}相對于{S}的位姿可以表示為gST(θ)：

(4)

1.2 機械臂正運動學建模

圖1和圖2分別為六自由度機械臂的三維模型圖和結(jié)構示意圖，其6個關節(jié)均為旋轉(zhuǎn)關節(jié)，前3關節(jié)和5、6關節(jié)軸線分別交于一點，第1和第2關節(jié)、第2和第3關節(jié)、第5和第6關節(jié)始終垂直，第4和第5關節(jié)異面垂直。

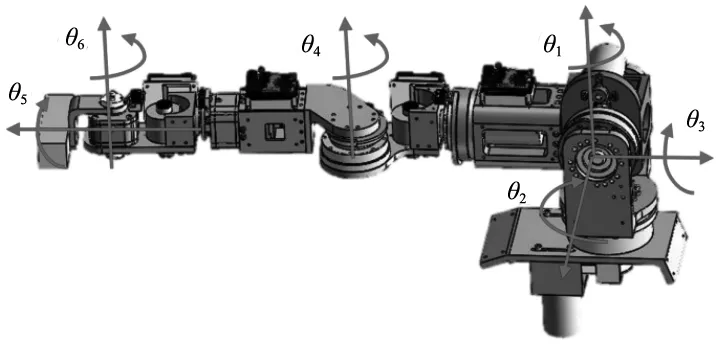
圖1 三維模型圖

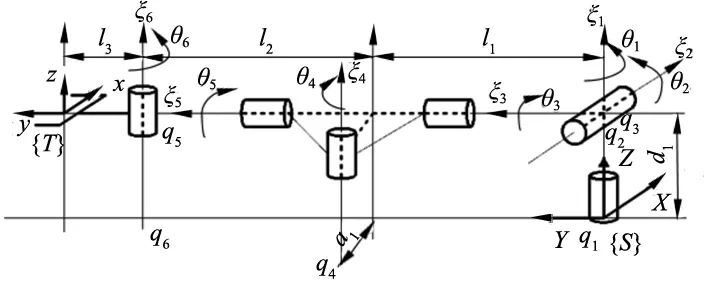
圖2 機械臂結(jié)構示意圖

選取初始位形如圖2所示，此時第1與第3關節(jié)垂直。在此初始位形下末端工具坐標系{T}在慣性坐標系{S}中的變換為：

(5)

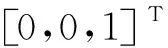
根據(jù)POE公式，可以得到六自由度機械臂的正運動方程：

(6)

2 機械臂逆運動學建模及簡化算法

2.1 基于panden-kahan子問題的逆解

機械臂的運動學逆解是已知末端的期望位置gST(θ)，求出該位置下對應的各關節(jié)角度。旋量逆解的基本思想就是將復雜的機器人運動學逆解，拆分成多個具有幾何意義明確的逆解子問題，當前公認的3個最基本子問題為paden-kahan的3個子問題[13]。

該六自由度機械臂是前3關節(jié)和5、6軸線分別交于一點，第4關節(jié)偏移中心軸線一定距離并與第5關節(jié)異面垂直；這樣的結(jié)構不能做簡單的拆分，所以不能直接利用paden-kahan的子問題求得逆解；這里我們需要利用前3關節(jié)和5、6關節(jié)分別相交一點的條件來消去其中的部分變量，才能將其轉(zhuǎn)化成相應的子問題，該結(jié)構機械臂的旋量運動學逆解具體求解如下。

(1)求解θ4

因為1、2、3關節(jié)和5、6關節(jié)軸線分別相交于一點，利用這一條件我們可以將除θ4以外的變量消去，這樣可以優(yōu)先求得θ4。

記機械臂的前3關節(jié)交于點p，p=q2=q3，第5和第6關節(jié)交于點q5。

(7)

第5、6關節(jié)軸線交于q5，轉(zhuǎn)動后位置不變，

(8)

式(7)兩端同時右乘q5有：

(9)

前3關節(jié)交于點p，有：

(10)

上兩式相減有：

(11)

在剛體旋轉(zhuǎn)的過程中，其上兩點之間的距離始終保持不變，并對上式兩端取范數(shù)：

(12)

那么θ4求解變成旋轉(zhuǎn)到指定距離的子問題3。

(13)

(2)求解θ5、θ6

由式(7)可得：

(14)

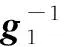
(15)

所以有：

(16)

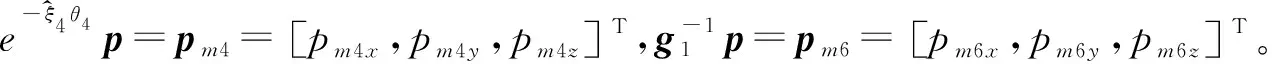
以上問題轉(zhuǎn)變成繞兩相交軸旋轉(zhuǎn)的子問題2。

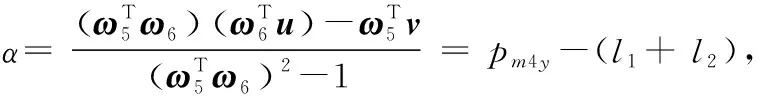
(17)

可以得到：

(18)

以上結(jié)果可以應用子問題1求得θ5、θ6：

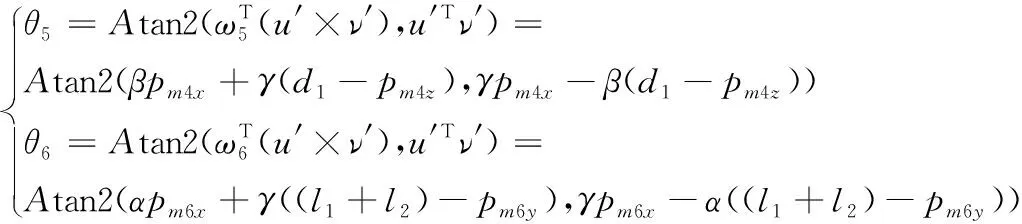
(19)

(3)求解θ1、θ2，

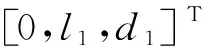
(20)

以上結(jié)果可以應用子問題2進行求得θ1、θ2，

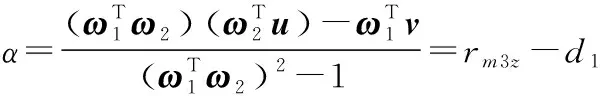
(21)

可以得到：

(22)

以上結(jié)果可以應用子問題1求得θ1、θ2，

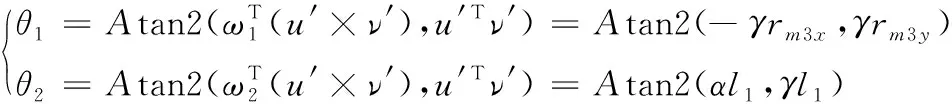
(23)

(4)求解θ3，

由式(7)可得下式，并記已知量為g3：

(24)

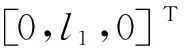
(25)

以上結(jié)果可以應用子問題1求解得θ3：

(26)

至此，已經(jīng)求解得到基于旋量六自由度機械臂的所有運動學封閉逆解。其中關節(jié)4有2組解，關節(jié)5與關節(jié)6組合有2組解，關節(jié)1與關節(jié)2組合也有2組解，所以該構型的機械臂共有8組解。

2.2 結(jié)合幾何法及歐拉角簡化前4關節(jié)角求解

2.2.1 幾何法簡化θ4的求解

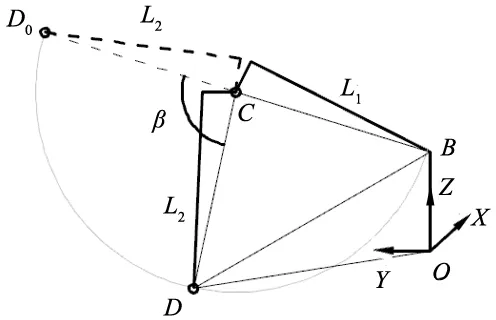
圖3 第4關節(jié)幾何關系圖

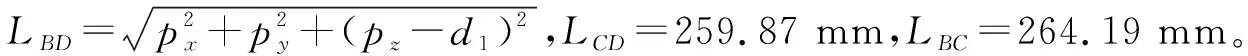
LBD2=LBC2+LCD2-2LBCLCDcos(π-β)

(27)

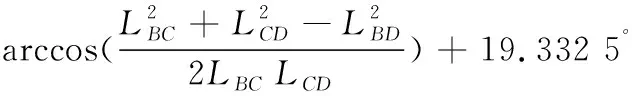
(28)

2.2.2 歐拉角簡化θ1,θ2,θ3的求解

在求得θ4,θ5,θ6的基礎上，可以通過以下關系求解θ1,θ2,θ3。

(29)

由于前3關節(jié)交于一點，第1關節(jié)與第2關節(jié)、第2關節(jié)與第3關節(jié)始終垂直，在初始位形下3個關節(jié)兩兩垂直，且3個軸都是純旋轉(zhuǎn)關節(jié)，在工具坐標系{S}下，θ1、θ2、θ3分別依次繞工具坐標系{S}的Z軸、X軸、Y軸轉(zhuǎn)動后的結(jié)果，可以等價為繞Z-X-Y順序的歐拉角變換結(jié)果：

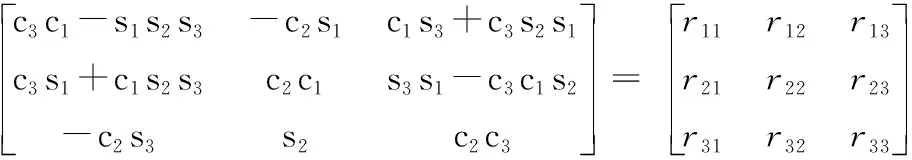
(30)

其中，c=cos,s=sin,1=θ1,2=θ2,3=θ3。

由式(30)、式(31)，通過以下關系可以求得θ1,θ2,θ3。

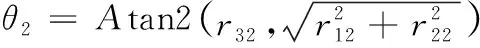
(31)

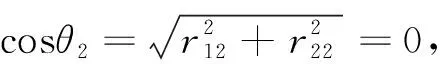
如果利用旋量理論和幾何法及歐拉角相結(jié)合來求解機械臂逆解，從上面可以看到，運動學逆解的求解過程和求解結(jié)果將得到很大簡化。

3 逆運動學實例驗證

六自由度機械臂的各個關節(jié)桿件參數(shù)如下：

d1=129.5 mm，l1=260.5 mm，a1=44 mm，l2=256.12 mm，l3=0 mm。

(1)任取一組不在奇異位形上的一組關節(jié)角，[θ1θ2…θ6]=[-66°55°-13°25°4°-10°]，將其帶入機械臂的正解公式中去，得到該組關節(jié)角對應末端姿態(tài)矩陣如下：

(32)

(2)利用前面推導的旋量逆解算法進行求解，得到機械臂各組關節(jié)角如表1所示，各組逆解位形如圖4所示。

表1 8組運動學逆解

續(xù)表

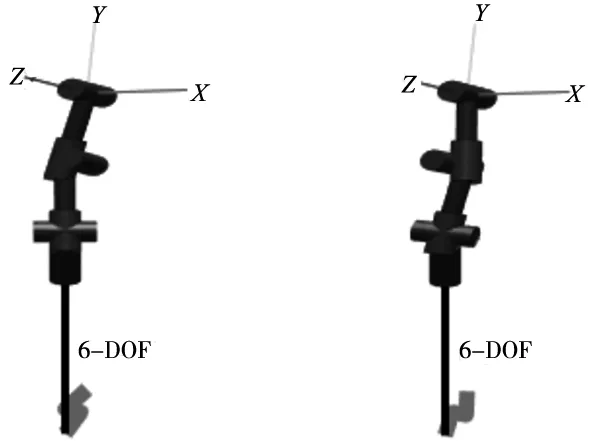
(a) 第1、2組解位形 (b) 第3、4組解位形

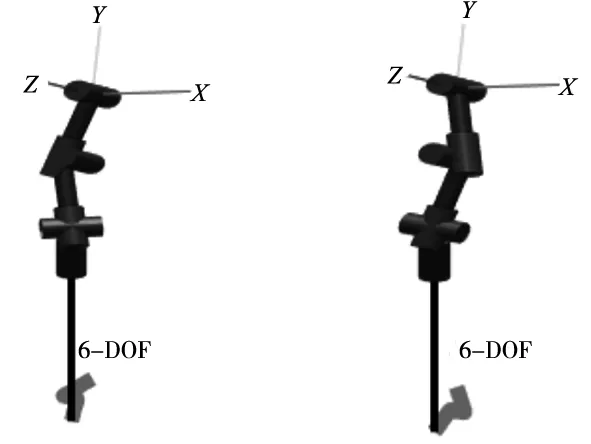
(c) 第5、6組解位形 (d) 第7、8組解位形圖4 8組逆解位形圖

表1的結(jié)果與前面分析一致，一共8組解，從上表可以看出，第8組解與我們?nèi)《ǖ年P節(jié)角一模一樣，1和2、3和4、5和6、7和8分別對應同一位形，8組解總共對應4種位形。

(3)再將以上8組解的結(jié)果再次帶入機械臂的正運動學公式中去，得到各組解對應的末端姿態(tài)矩陣，可以看到以上8組解對應著幾乎相同的末端姿態(tài)矩陣，這里再一次證明該算法的正確性；將得到的8組解對應的末端矩陣與給定角度對應的末端矩陣做差，結(jié)果看作各組解的誤差，其中第4組解的誤差最大，為：

(33)

最大誤差在10-13數(shù)量級，該算法具有非常高的精度。實際應用中，需要對求得的多組解進行篩選，要求各個關節(jié)要在機械臂的運動范圍內(nèi)、避開機械臂的各個奇異位形和工作范圍內(nèi)的障礙物等，再根據(jù)運動行程最短等尋優(yōu)條件去選擇一組最優(yōu)解。

(4)同樣的，取式θ5=4°,θ6=-10°和式(32)的末端姿態(tài)，帶入簡化算法中可以得到：[θ1θ2θ3θ4]=[-66°55°-13°24.992 2°]，該結(jié)果與給定關節(jié)角幾乎一樣，驗證了簡化算法的正確性。

4 結(jié)束語

(1)結(jié)合旋量理論和已知的paden-kahan子問題，推導出前3關節(jié)、第5、6關節(jié)分別相交于一點，第4關節(jié)偏移的六自由度機械臂運動學逆解。該方法相對于傳統(tǒng)的D-H法，其幾何意義明顯，過程和結(jié)果都更加簡潔，并且算法精度能夠達到10-13數(shù)量級，有非常高的精度，能夠很好的滿足各種應用的控制需求。

(2)采用歐拉角及幾何法對前3關節(jié)和第4關節(jié)運動學逆解算法進行簡化改進，應用旋量理論、歐拉角和幾何法相結(jié)合求取運動學逆解，能夠極大的簡化過程和結(jié)果。

(3)本文提出的方法適用于其他類似構型，特別是前3關節(jié)交于一點構型機械臂的運動學逆解，具有一定通用性。