鈦合金超聲橢圓振動銑削殘余應力有限元仿真*

申 奧，牛雪梅，閆獻國，陳 峙，黃 堯，樊佳琪，孟 宇

( 太原科技大學 a．機械工程學院; b．電子信息工程學院，太原 030024)

0 引言

鈦合金具有低密度、高強度以及良好的抗腐蝕能力等特點，廣泛地應用在航空航天領域[1]。由于鈦合金本身的低熱傳導特性，導致在機加工中產生較大的殘余應力[2]。殘余應力的存在會降低鈦合金疲勞強度、引起應力腐蝕和導致工件變形[3]。研究表明，相比于傳統切削，超聲振動切削能夠有效地減少切削殘余應力[4]。羅海泉等研究了在徑向方向給工件施加超聲振動時，銑刀進給速度和超聲振幅對切削力的影響[5]。王明海等通過ABAQUS軟件研究了超聲振動參數和切削參數對鈦合金加工表面殘余應力的影響，并通過試驗驗證了仿真結果的準確性[6]。許東輝等通過有限元軟件研究了在相同切削參數下，傳統切削、橫向振動切削和縱向振動切削對表層殘余應力的影響[7]。何俊等運用有限元軟件研究了橢圓軌跡參數：振幅、振動頻率和相位差對TC4鈦合金銑削加工過程中切削熱的影響[8]。

從目前的研究來看，由于超聲橢圓振動切削技術系統的復雜性[9]，實驗中的殘余應力難以測量，主要運用有限元技術進行模擬仿真，但目前的研究主要是針對二維有限元模型的仿真，在三維殘余應力模型方面的研究較少，本文運用有限元方法研究超聲橢圓振動切削技術中進給方向上的振動參數和切削參數對工件殘余應力的影響。

1 Ti6Al4V超聲橢圓銑削有限元模型

采用硬質合金YG8刀具，通過三維軟件對銑刀和工件進行建模，銑刀和工件模型如圖1所示。其中銑刀直徑為φ8 mm，前角為10°，后角為15°，為了提高計算時間，減小網格數量，銑刀長度為5 mm，工件尺寸為3 mm×2 mm×2 mm，對工件切削層網格加密，同時將銑刀定義為剛體。由于在銑削過程中會產生大量的切削熱，切削熱對工件的殘余應力有顯著的影響[10]，所以工件和刀具的網格選擇八結點六面體的C3D8RT。

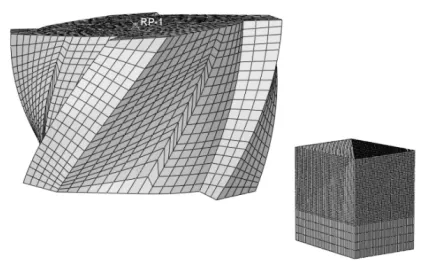
圖1 刀具和工件模型

1.1 工件材料物理屬性及損傷模型參數的定義

工件材料為Ti6Al4V鈦合金，刀具材料為YG8硬質合金，其物理屬性見表1[11]。

表1 刀具材料和工件材料的物理屬性

目前在切削仿真實驗中，用到最多的本構模型為Johnson-Cook模型(J-C模型)[12]，其模型結構，如公式(1)所示：

(1)

其中，σ為材料的流動應力;εp為等效塑性應變;ε為等效塑性應變率;ε0為材料參考應變率;T為工件溫度;T0為常溫系數;Tmelt為材料的熔點;A為準靜態條件下的屈服強度;B為應變硬化參數;C為應變率強化參數;n為硬化指數;m為熱軟化參數。表2為Ti6Al4V鈦合金J-C模型參數[11]。

表2 Ti6Al4V鈦合金J-C模型參數

切屑的分離準則選用Johnson-Cook動態失效模型，該模型應用于高應變率金屬的變形，以材料模型的逐漸損壞。當損傷參數ω達到1時，表示單元破壞，材料發生破壞分離[13]。如公式(2)所示，損傷參數ω的定義為：

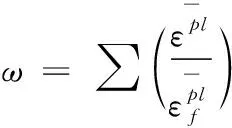
(2)

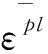
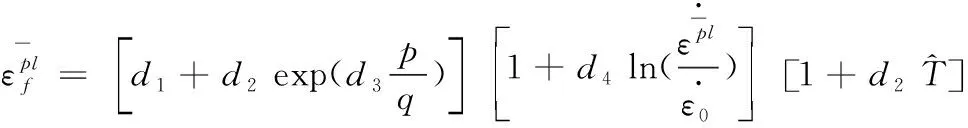
(3)

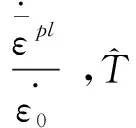
表3 Ti6Al4V鈦合金J-C動態失效模型參數

1.2 超聲載荷

通過給刀具邊界載荷施加周期幅值，以達到刀具實驗超聲橢圓振動的效果，ABAQUS中周期型幅值曲線函數用傅里葉級數來表示[14]，其表達式如下所示：

t≥t0時：

(4)

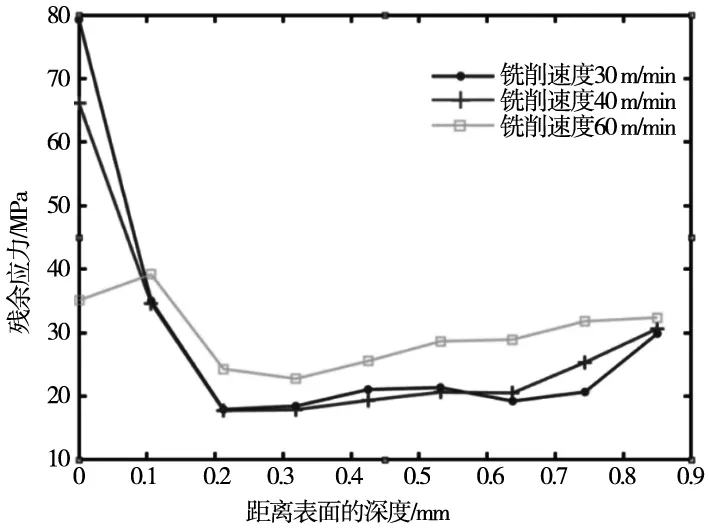
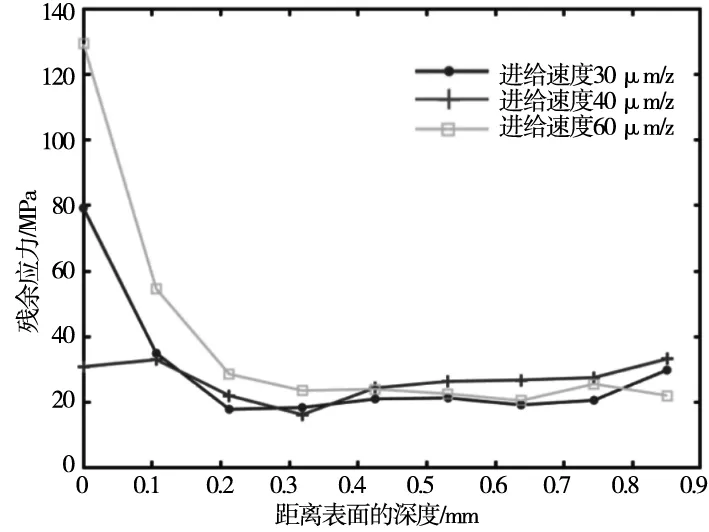
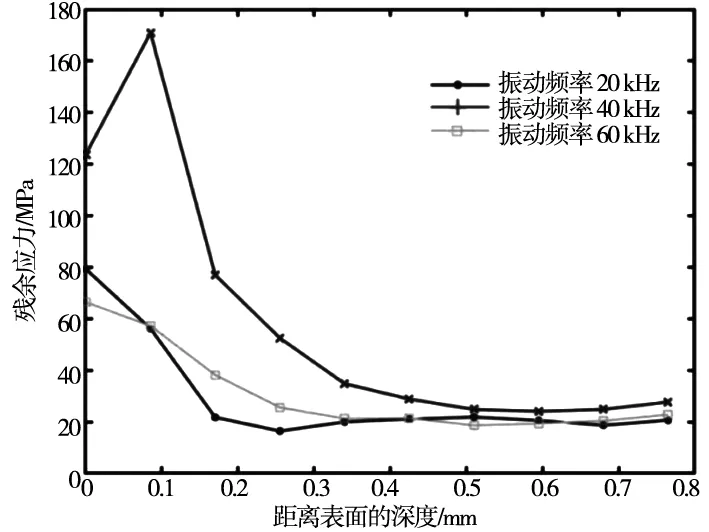
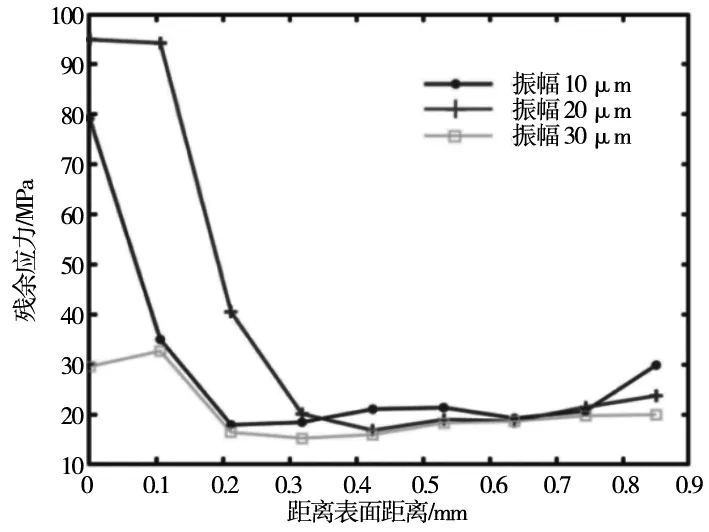
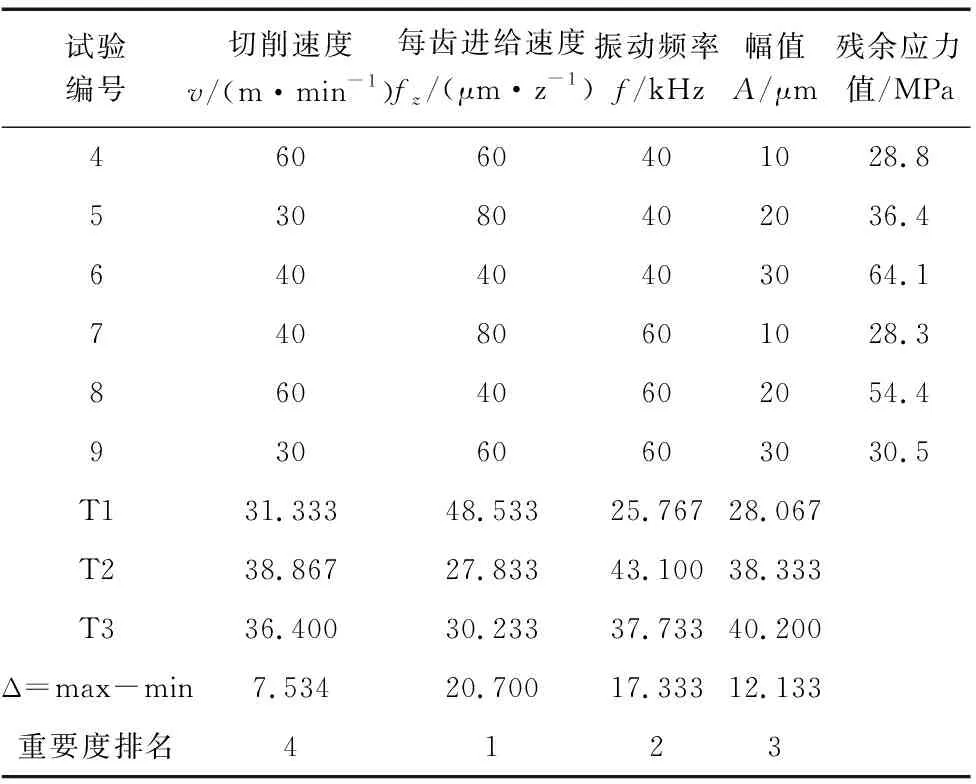
t

a=A0

(5)

式中，N為傅里葉級數項的個數；ω為圓頻率，單位為rad/s；t0為起始時刻；A0為初始幅值；An為cos項的系數(n=1,2,3,…,N) ；Bn為sin項的系數。

上述式中給出的是刀具相對與工件的位移方程，通過對上述位移方程進行一階導數求得刀具相對于工件的速度方程：

x′=-Aωsinωt+A0
y′=-Bωcosωt

(6)

1.3 邊界條件的施加

銑削切削仿真中，將工件底面結點的6個自由度進行限制以達到固定工件目的，如圖2所示。同時為了模擬其真實的銑削過程，對刀具參考點要設置其軸向角速度和沿工件方向的位移速度，以實現刀具的旋轉運動和對工件的進給運動。

圖2 工件邊界載荷的施加

2 超聲橢圓振動銑削仿真單因素仿真分析

2.1 實驗設計

如表4所示，由文獻[5-7]可知，在超聲橢圓振動銑削仿真實驗中，影響工件殘余應力的主要因素為：進給方向上的振動頻率和幅值以及刀具的銑削速度和進給速度。

表4 單因素超聲振動參數

2.2 銑削速度對殘余應力的影響

單因素仿真實驗，為研究銑削速度對工件殘余應力的影響，控制fz為30 μm/z、f為20 kHz，A為10 μm，通過改變銑削速度v的值，來確定銑削速度對工件殘余應力的影響。銑削結果如圖3所示。

圖3 超聲橢圓振動銑削仿真應力分布圖

如圖4所示， 銑削速度v=30 m/min和銑削速度v=40 m/min時，沿深度方向的殘余應力變化趨勢大致相同，殘余應力值均在大約0.2 mm處達到最小，然后隨深度的增加殘余應力值有緩慢上升趨勢。而銑削速度=60 m/min時，表面殘余應力值最小，在距離表面深度0.1 mm處達到最大值，而后殘余應力值隨深度的增加先減小后又緩慢上升。從深度方向看，銑削速度為60 m/min殘余應力值總體大于銑削速度為30 m/min和40 m/min的殘余應力，這是由于隨著銑削速度的增加，銑刀和工件的摩擦也相應的增多，在銑削區域產生更多的切削熱，使得已加工表面和工件內部的溫差增大從而殘余應力也更大。

圖4 銑削速度對殘余應力的影響

2.3 進給速度對殘余應力的影響

控制銑削速度為30 m/min、振動頻率為20 kHz，振幅為10 μm。通過改變fz的值，來確定進給速度對工件殘余應力的影響。

如圖5所示，進給速度為40 μm/z時表面殘余應力值最小30 MPa，進給速度率為60 μm/z時表面殘余應力值最大130 MPa。當進給速度為30 μm/z和60 μm/z時，殘余應力的值隨深度的增加而減小，在距離表面0.3 mm 深度時殘余應力值達到最小值，而后在深度方向殘余應力基本穩定。進給速度為40 μm/z時，在深度方向殘余應力的值基本趨于穩定。當距離表面深度大于0.2 mm以后，進給速度為30 μm/z、40 μm/z、60 μm/z三者殘余應力值均在30 MPa左右。這是由于隨著fz的增大，切削的厚度也相應增加，故切屑帶走的切削熱也增大，同時fz的增大，切削力也隨之增大，刀具和工件之間的摩擦產生更多的切削熱量，從而使工件內部的殘余應力增大。

圖5 進給速度對殘余應力的影響

2.4 振動頻率對殘余應力的影響

控制銑削速度為30 m/min、每齒進給量為30 μm/z，振幅為10 μm。通過改變振動頻率，來確定振動頻率對殘余應力的影響。

如圖6所示，振動頻率為60 kHz時表面殘余應力值最小68 MPa，振動頻率為40 kHz時表面殘余應力值最大122 MPa。當振動頻率為40 kHz和60 kHz時，其殘余應力的值均沿著深度方向降低，在大約0.25 mm深時殘余應力達到最小。而當振動頻率為40 kHz時，其殘余應力值沿深度方向先增大，在0.1 mm深度時達到最大殘余應力172 MPa，而后沿深度方向快速減小，在大于0.4 mm深度后殘余應力趨于穩定在20 MPa左右。這是因為在超聲振動中刀具和工件是周期性接觸，隨著頻率的增大，刀具和工件的接觸時間更短，從而切削熱的能夠更快的消散，所以殘余應力的大小隨振動頻率的增加而減小。

圖6 振動頻率對殘余應力的影響

2.5 振幅對殘余應力的影響

控制銑削速度為30 m/min、每齒進給量為30 μm/z，振動頻率為20 kHz。通過改變振幅，來確定振幅對工件殘余應力的影響。

如圖7所示，振幅為30 μm時表面殘余應力值最小30 MPa，振幅為20 μm時表面殘余應力值最大95 MPa。當振幅為20 μm和30 μm時，殘余應力值在深度0.1 mm內變化很小，當深度大于0.1 mm后殘余應力應力迅速減小。振幅為10 μm時，其殘余應力隨深度的增加快速減小，在大于0.2 mm深后殘余應力值穩定在20 MPa左右。這是因為振幅的增大，超聲振動銑削斷續加工的特點更加突出，刀具和工件的斷續接觸，使切削熱引起的殘余應力更小。

圖7 振幅對殘余應力的影響

3 超聲橢圓振動加工參數優化

3.1 正交試驗的設計

如表5所示，建立正交試驗對超聲橢圓加工參數進行優化，影響因素A、B、C、D主要為上述單因素實驗中v、fz、f和A。

表5 正交試驗水平及因素

3.2 正交試驗結果及分析

通過表6可知，4個影響因素對實驗結果的影響程度各不相同，依據極差法其主次排名為fz>f>A>v。通過正交試驗法得出的優化實驗參數：每齒進給速度為60 μm/z，振動頻率為20 kHz，振幅為10 μm，切削速度為30 m/min。通過ABAQUS得到該優化后的實驗組結果為，24.1 MPa。

表6 正交試驗數據及分析

續表

4 結論

(1)在單因素實驗中，在給定的研究范圍內，切削因素對工件殘余應力的影響為：切削速度和進擊速度的增大，加劇了刀具和工件之間的摩擦，產生更多的切削熱，導致殘余應力增大。

(2)在單因素實驗中，在給定的研究范圍內，振動參數對工件殘余應力的影響為：振動頻率和振幅的增大，使刀具和工件接觸時間更短，切削熱更易消散，導致殘余應力減小，結果與文獻一致。

(3)在正交試驗中，對工件的殘余應力影響程度從大到小依次為：每齒進給速度、振動頻率、幅值、切削速度。其優化參數組合5為：每齒進給速度為60 μm/z，振動頻率為20 kHz，振幅為10 μm，切削速度為30 m/min。通過ABAQUS得到優化后的實驗組結果為24.1 MPa。