汽車車門多學科性能分析與輕量化多目標優化設計

熊鋒，黃家樂，余鑫，梁子豪，劉昊巖，夏康星

(重慶理工大學車輛工程學院，重慶 400054)

0 引言

隨著汽車需求量的逐步增長，汽車帶來的環境問題和安全問題越來越明顯。汽車車門作為車身的重要部件，對其進行性能優化與輕量化設計具有較為重要的意義。史朝軍[1]建立車門的有限元模型，由HyperMesh分析得到車門的多項性能指標，建立多學科設計優化模型。在HyperStudy中進行DOE靈敏度分析，構造各個性能的近似響應面，基于響應面應用遺傳算法進行多學科設計優化。欒文哲[2]對車門進行側面柱碰撞分析，同時基于響應面對車門進行模態優化設計。高杰[3]對車門進行動靜態分析，在此基礎上通過靈敏度分析對變量進行篩選，在Isight軟件中進行多目標優化。韋永平[4]對車門外板進行抗凹分析和抗擠壓分析，對性能不足的部件進行優化改進，提高了車門抗擠壓性能等。通過對前人工作的了解，本文作者對車門進行較為完整的多學科性能分析及輕量化設計優化[1]。

1 優化過程理論與技術路線

1.1 Plackett-Burman設計

Plackett-Burman設計是一種兩水平的試驗設計方法，它試圖以最少的試驗次數達到使因數主效果得到盡可能準確地估計。適用于從眾多考察因素中快速有效地篩選出最為重要的幾個因素[2]。

1.2 哈默斯雷設計

哈默斯雷采樣(Hammersley Sampling)(本質上屬于類蒙特卡洛方法)，采用Hammersley法進行試驗設計(DOE)，通過偽隨機數值發生器，在超立方體中均勻地進行抽樣。相比以往的拉丁超立方抽樣，Hammersley采樣法能在k維超立方中實現很好地均勻分布,有效地改善了設計樣本的均勻性。

1.3 HyperKriging

HyperKriging在統計學中是從每個變量的相關性出發，在有限的區域內對變量進行無偏、最優估算的一種方法。該方法用于空間中變量存在相關性的情況。

1.4 多目標遺傳算法

多目標遺傳算法(NSGA-Ⅱ)，它克服第一代遺傳算法的缺陷并且通過擁擠度來度量系統元素的分布情況，從而選擇那些分布均勻，獲得信息多的基因。遺傳算法在求解時不受優化函數連續性的限制，可直接以個體適應度為條件進行搜索，具有很高的并行性[5]。

2 有限元模型建立

文中所研究的汽車車門采用沖壓件分體式車門，車門結構如圖1所示。

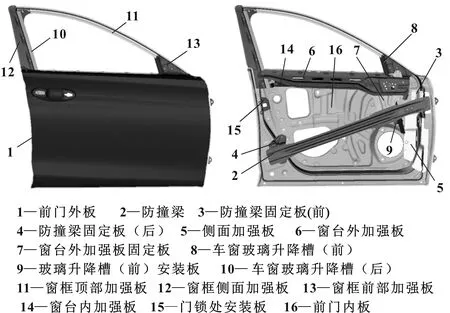
圖1 車門結構

2.1 有限元模型建立

首先對車門模型進行幾何清理，然后按照圖2的流程建立車門有限元模型，最后根據企業標準檢測網格質量，并調整網格至符合企業標準。

圖2 有限元模型建立流程

2.2 連接方式的模擬

HyperWorks中有豐富的連接設置方式，車門中常用的連接方式有點焊連接、膠粘連接、螺栓連接、鉸鏈連接等類型。

2.2.1 點焊模擬

ACM(Area Contact Model)模型為文中采用的焊點模擬模型。該模型是由一個處于兩個焊接件之間并且垂直于被焊面的六面體單元通過柔性連接RBE3單元和兩個被焊件連接而成。同時六面體的尺寸和焊核的尺寸一致。焊點受到的載荷通過RBE3單元擴散到被焊件的多個節點。載荷的大小以及擴散的方向由RBE3單元的權重所決定的[6]。

2.2.2 膠粘模擬

膠粘模型，其主體是一排Hexa/Penta單元，同時頭部創建許多RBE2/RBE3單元。如果在連接器區域有明顯的曲率，則會創建Penta元素，否則通常會創建Hexa元素。如果有一個直接的正常項目，那么將使用RBE2元素;如果只有非正常的投影，那么將創建RBE3元素[7]。

2.2.3 鉸鏈模擬

鉸鏈連接的建模是通過在HyperMesh的1D菜單下的FE joints菜單來進行搭建的，通過建立轉動鉸(Revolute)來模擬車門鉸鏈。

3 車門動靜態特性分析

根據企業標準設置各工況下的載荷及約束，對車門進行動靜態特性分析。主要對車門進行的靜態分析包括下沉工況剛度，上、下扭轉工況剛度，內、外板帶線工況剛度以及窗框的中部與邊角工況剛度分析。在動態特性分析中，進行了約束模態分析。

3.1 下沉工況

車門把手處施加垂直向下750 N的力。其約束條件為：(1)上下鉸鏈處6個自由度；(2)門鎖處Y平動自由度。

如圖3所示，在車門下沉工況分析中，最大位移處位移量為6.296 mm>6 mm，不符合企業標準，應該對下沉工況剛度進行優化，使其到達企業標準。

圖3 車門下沉工況分析及位移云圖

3.2 車門上扭轉工況

在靠近車門鎖處一側上方施加183 N沿Y方向向外的力。其約束條件：(1)上下鉸鏈處6個自由度；(2)門鎖處X,Y,Z平動自由度。

如圖4所示，在車門上扭轉工況分析中，最大位移處位移量為0.562 mm，符合企業標準。

圖4 車門上扭轉工況分析及位移云圖

3.3 車門下扭轉工況

在靠近車門鎖處一側下方施加183 N沿Y方向向外的力。其約束條件：(1)上下鉸鏈處6個自由度；(2)門鎖處X,Y,Z平動自由度。

如圖5所示，在車門下扭轉工況分析中，最大位移處位移量為1.392 mm，符合企業標準。

圖5 車門下扭轉工況分析及位移云圖

3.4 內板帶線工況

在靠近車門內板帶線處施加80 N垂直于接觸面方向力。其約束條件為：帶線以下的位置均勻的對三處進行全約束。

如圖6所示，在車門內板帶線工況分析中，最大位移量為0.616 mm，符合企業標準。

圖6 車門內板帶線工況分析及位移云圖

3.5 外板帶線工況

在靠近車門外板帶線處施加80 N垂直于接觸面方向力。其約束條件為：帶線以下的位置均勻的對三處進行全約束。

如圖7所示，在車門外板帶線工況分析中，最大位移量為0.367 mm，符合企業標準。

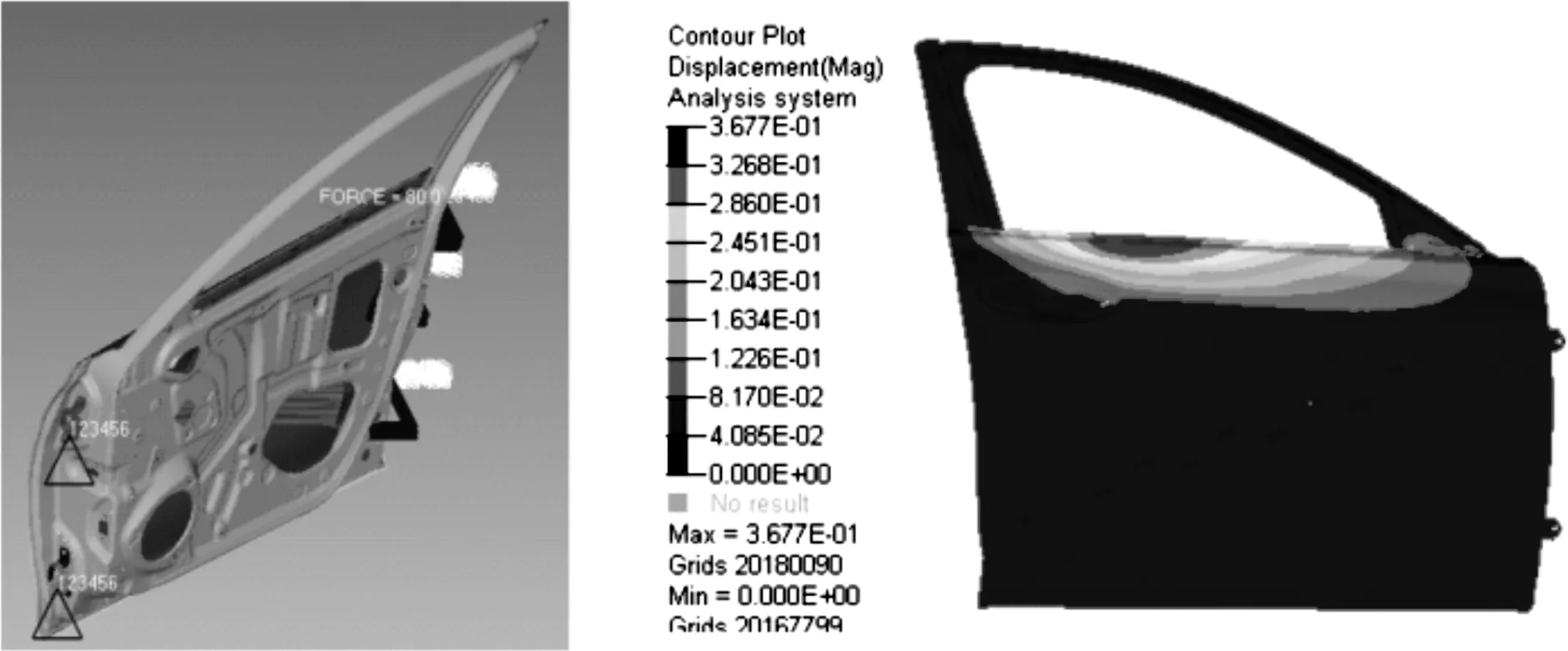
圖7 車門外板帶線工況分析及位移云圖

3.6 窗框中部工況

在靠近車門中部位置施加200 N垂直于車門向里的力。其約束條件為：帶線以下的位置均勻的對三處進行全約束。

如圖8所示，在窗框中部工況分析中，最大位移量為6.68 mm>6 mm，不符合企業標準要求。因此，在后續的優化中，應該對窗框中部剛度進行優化，使其到達企業標準。

圖8 窗框中部工況分析及位移云圖

3.7 窗框邊角工況

在靠近車門邊角位置施加250 N垂直于車門向里的力。其約束條件為：帶線以下的位置均勻的對三處進行全約束。

如圖9所示，在窗框邊角工況分析中，最大位移量為3.09 mm，符合企業標準。

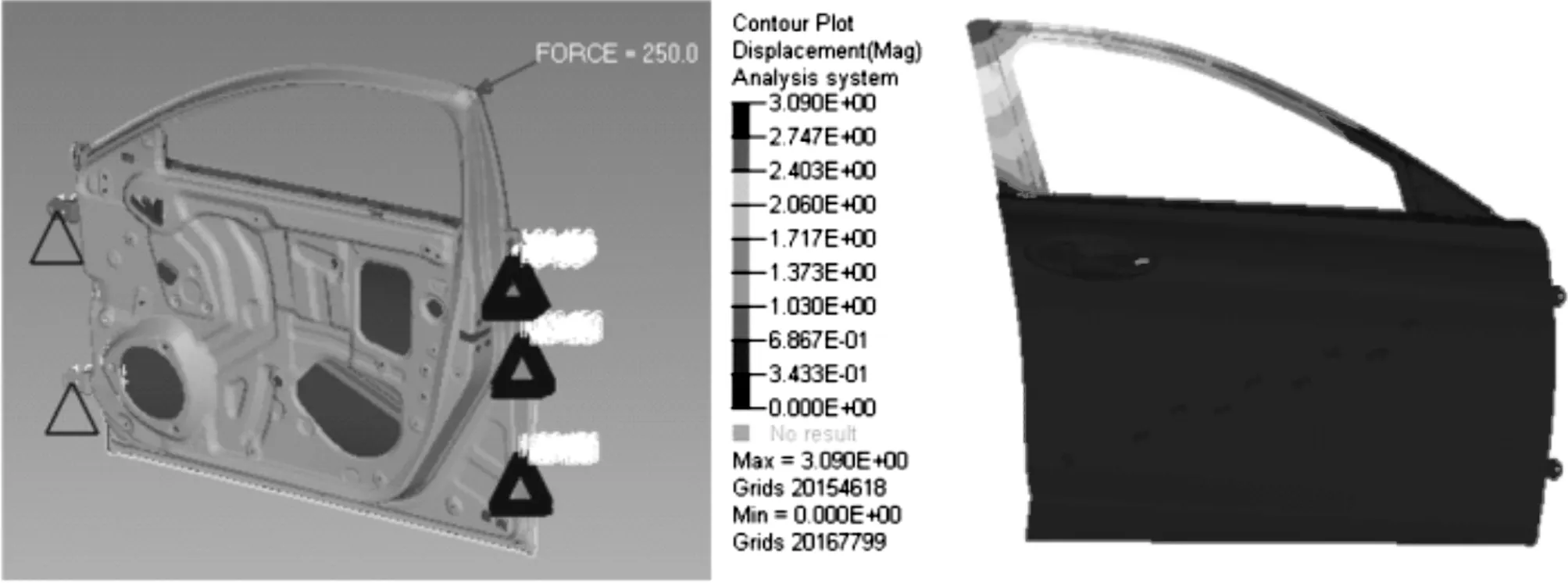
圖9 窗框邊角工況分析及位移云圖

3.8 約束模態分析

對門鎖和鉸鏈處進行全約束。如圖10所示，一階模態頻率為30.3 Hz>30 Hz符合企業標準，但與許用值較近。后續應對其進一步優化，以提高一階模態頻率。

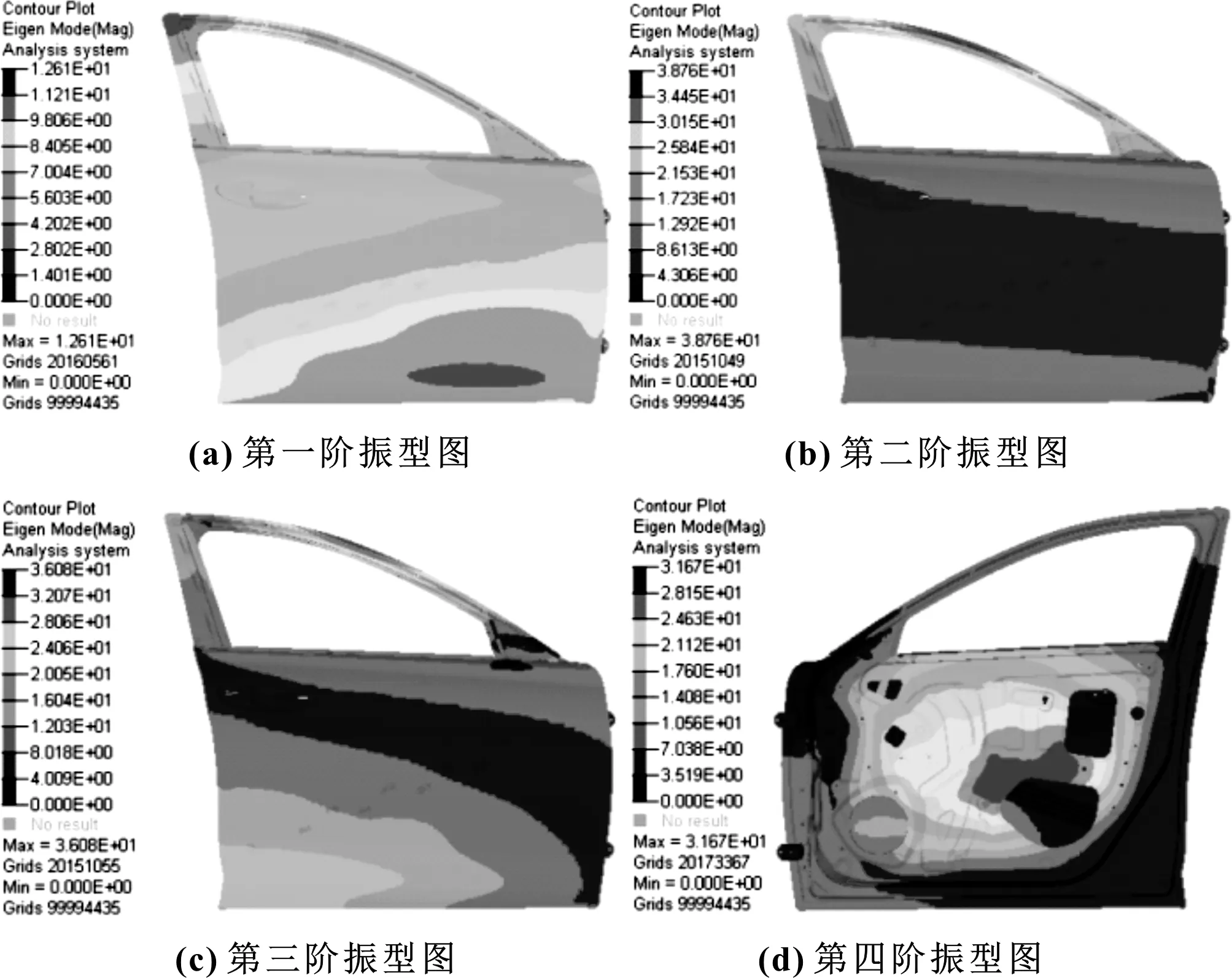
圖10 車門前四階振型圖

表1為車門低階模態情況。

表1 車門低階模態情況

4 基于LS-DYNA的車門碰撞分析

4.1 有限元模型建立

車門有限元模型約束：主要包括對鉸鏈和車門門鎖的約束，上、下鉸鏈與車身側圍連接處全約束，鉸鏈轉軸與門鎖處的約束為3個平動自由度和2個轉動自由度，車門可以繞鉸鏈軸進行轉動。

同時，在車門上邊緣部分要添加焊縫作為一整個剛性體。對于側面碰撞仿真采用的剛性柱，參照碰撞規則，車門和剛性柱在Y方向具有相對速度，從而發生碰撞。

4.2 碰撞模型的簡化

文中車門有限元模型的求解參考中汽研C-NCAP管理規則(2018年版)中側面碰撞試驗程序，移動變形壁障總質量為(1 400±20)kg。

碰撞前，壁障高度應滿足如下靜態測量要求：梁單元前面最上(吸能塊上下行相交部分)部分距離地平面的高度為(600±5)mm[9]。

移動變形壁障速度要求為50～51 km/h，該速度至少在碰撞前1 m內保持穩定。速度控制精度為±0.2 km/h。記錄移動變形壁障實際速度。

文中采用剛性柱代替移動變形壁障，中柱體相對于車門的速度為80 km/h(高于標準)，整個碰撞時間設置為15 ms。對剛性柱進行質量設置，賦予質量1 400 kg。剛性柱整體高度為600 mm。關注的指標簡化為車門在碰撞方向的損傷和形變。

4.3 材料選取和接觸設置

MAT20是剛體材料模型，該材料模型具有不可壓縮、變形的特性，材料模型內各點之間的相對位置保持不變，因此碰撞時的剛性柱材料選擇為MAT20，同時設置車門與剛性柱的相對速度和整個碰撞的總時長。時間步長等參數選取默認值。

側面碰撞的接觸設置，由于車門和剛性柱之間存在一個距離，因此在設置接觸時采用存在距離的面面接觸(Surface To Surface)，而車門整體之間采用單面接觸(Sigle Surface)模擬，靜摩擦和動摩擦因數均選定為0.4。

4.4 碰撞過程模擬及結果分析

對車門有限元模型的求解中，柱體相對于車門的速度為50 km/h，整個碰撞時間為15 ms。

在剛性柱與車門的碰撞過程中，如圖11所示，動能最大值為2.4 kJ，且可以觀察到在5.02 ms時發生碰撞，動能開始非線性減少至0.497 kJ，由圖11觀察到內能由未發生碰撞時0 kJ非線性增長至最大值1.78 kJ。整個車門側面剛性柱碰撞過程能量守恒。剛性柱產生的大部分動能通過與車門撞擊由車門結構的變形所吸收，轉化為車門的內能，其余的能量以熱能、聲能等形式消耗掉。

圖11 碰撞過程動能和內能曲線

在碰撞發生過程中，車門沿碰撞方向發生的形變與時間同樣呈現非線性關系，圖12為碰撞過程中車門所發生的形變與時間的關系。

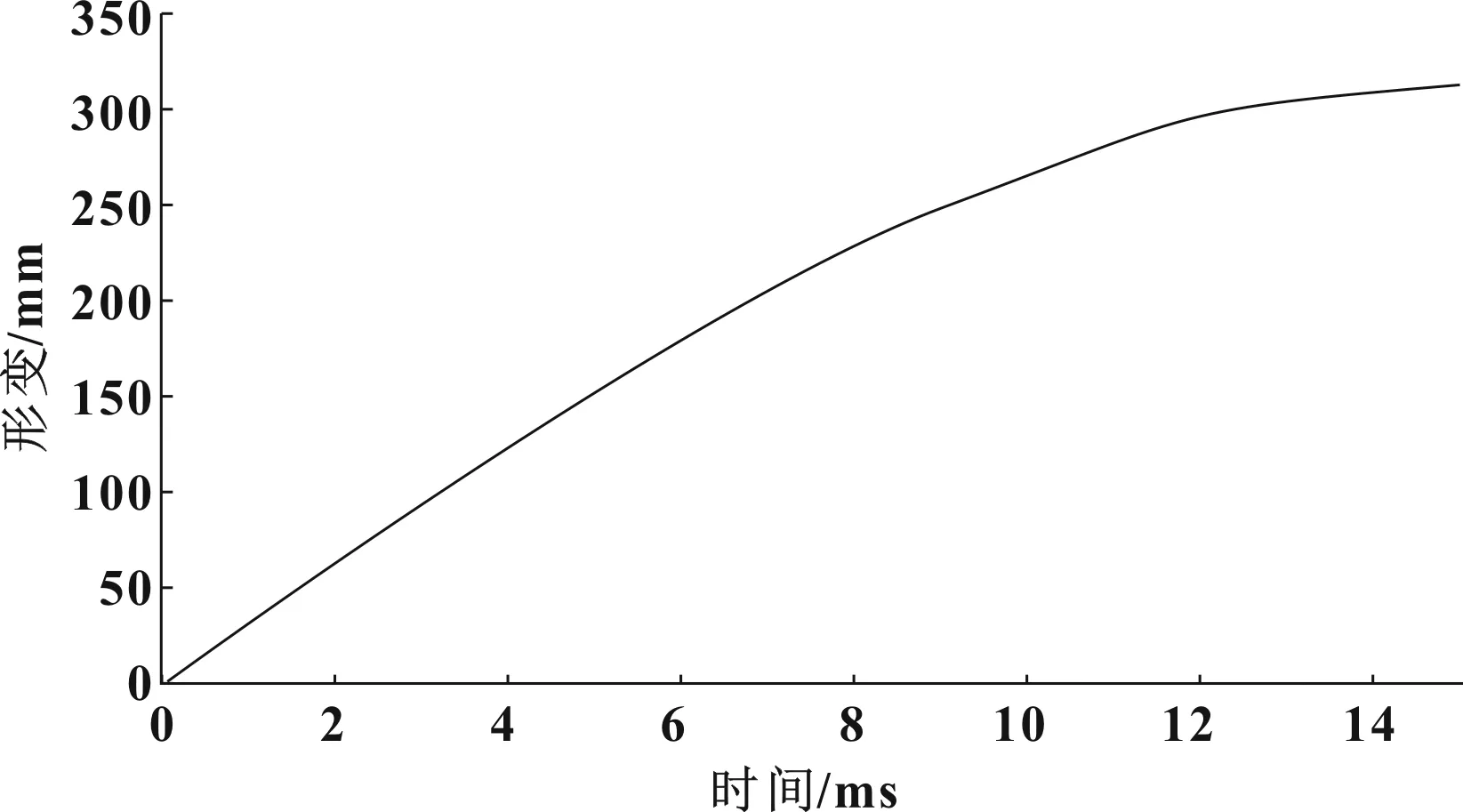
圖12 車門形變與時間的關系曲線

在車門發生不同形變的情況下，能量的吸收也不同。如圖13所示，分別是碰撞發生5 ms、10 ms時車門所發生的形變，在碰撞發生5～10 ms這一時段內，可以觀察到車門整體的形變增量不大，車門并沒有產生過大的凹曲變，碰撞發生10 ms時，可以從圖中觀察到，車門外板、內板產生接觸，同時，車門內、外板的加強板也發生接觸現象,如圖14所示。

圖13 碰撞發生5 ms、10 ms位移云圖

圖14 碰撞發生10 ms時車門內部結構

由于加強板的存在，使得車門內部的形變在云圖中大部分呈現深灰色，形變的量維持在安全范圍內，同時也降低了由于碰撞過程中車門變形嚴重導致車門無法打開情況的概率。

5 基于多目標的車門輕量化設計

5.1 優化目標及約束條件的建立

文中研究的車門初始質量為17.5 kg。在前文約束模態分析中，一階頻率為30.3 Hz。雖然大于30 Hz，但仍需優化使設計偏于安全。窗框中部剛度工況和下沉工況分析中最大位移量超過企業要求的6 mm位移量。

對于多目標函數最優化問題，考慮到目標函數的重要程度不一樣的情況，先應抓住主要目標，同時兼顧次要目標要求。在4個響應中，輕量化為預期目標，模態頻率為次要目標，窗框中部剛度工況最大位移量和下沉工況最大位移量為限制條件。因此，文中將車門質量最小作為主要目標，一階模態頻率作為次要目標。將窗框中部剛度工況最大位移量和下沉工況最大位移量小于6 mm作為約束。

建立優化數學模型為：

式中：S為該工況下實際最大位移量；D為該工況下允許的最大位移量；T為車門板件類零件厚度;i為設計變量代號。

5.2 基于靈敏度的優化設計變量篩選

文中分析的前車門主要板件類零件共有16個，如果全部參與試驗，則需要的試驗次數多。因此，在試驗設計需要預先進行一次靈敏度分析，通過主效應圖對設計變量進一步篩選。零件厚度變量上下限為初始值±34%。

將設計變量導入并預先進行一次試驗設計。采用的試驗設計方法為Plackett-Burman設計，獲得主效應圖，由主效應圖找到所需設計變量。如圖15—17所示為厚度變量與響應的關系。

圖15 一階頻率與厚度變量的主效應圖

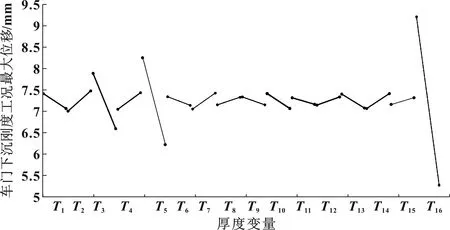
圖16 下沉剛度最大位移量與厚度變量的主效應圖

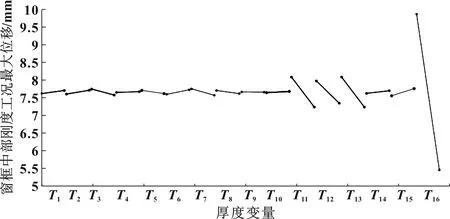
圖17 窗框中部剛度最大位移量與厚度變量的主效應圖

由主效應圖可以得出：

(1)厚度變量與一階模態既有正相關也有負相關，篩選的原則是希望負相關，即隨著厚度的減小，一階模態頻率增加，T1、T2、T15滿足條件。

(2)厚度變量與下沉剛度最大位移量既有正相關也有負相關，篩選的原則是希望正相關，即隨著厚度的減小，下沉剛度的最大位移量減小，T2、T4、T7、T14滿足條件。

(3)厚度變量與窗框角部剛度的最大位移量既有正相關也有負相關，篩選的原則應該是正相關，但是從主效應圖中線條的斜率看出，沒有較強相關性的正相關厚度變量。因此，文中選擇相關性較大的厚度變量，即厚度變厚，可以有效地使位移量減小。此次優化選擇T12、T13、T16。

同時，為了避免厚度改變導致碰撞性能的降低，不選擇T2(防撞梁)作為變量。綜上所述,選擇的變量為T1、T4、T7、T12、T13、T14、T15、T16。

5.3 試驗設計

將篩選后的8個設計變量和4個響應導入，選擇Hammersley法進行試驗設計(DOE)，得到的數據將用于近似模型的構建。

5.4 近似模型的構建

將第二次試驗設計的數據導入，并選擇HyperKriging法擬合模型。

5.5 多目標優化執行與結果分析

文中選擇多目標遺傳算法(Multi-Objective Genetic Algorithm)作為優化的方法。質量與一階模態頻率Pareto非劣解集如圖18所示。

圖18 質量與一階模態頻率Pareto非劣解集

如圖19所示為優化模型迭代數據，黑色部分即為符合約束條件和目標的數據。文中選擇了灰色行數據。將優化前后的厚度變量進行對比，結果見表2。

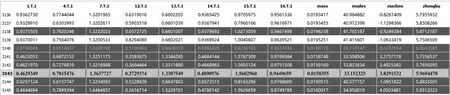
圖19 優化模型迭代數據

表2 優化前后厚度變化 mm

5.6 優化結果檢驗

將厚度改為優化值并重新進行分析，得到優化前總質量為17.5 kg，優化后總質量為17.27 kg，質量減輕0.23 kg；同時，一階約束模態頻率由30.03 Hz，提升到32.39 Hz，提高7.86%；在中部角度剛度分析中，最大位移也由6.69 mm變為5.67 mm，滿足要求。優化前后結果如圖20—22所示。

圖20 下沉工況優化前后對比

圖21 窗框中部剛度優化前后對比

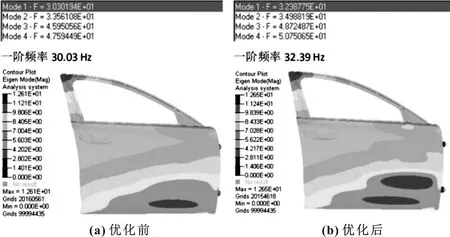
圖22 一階約束模態頻率優化前后對比

6 結論

(1)文中對車門進行多學科性能分析及多目標優化設計，實現了輕量化及性能提升的目的。分析流程能夠推廣到其他的部件設計中，具有普適性。

(2)文中通過主效應圖對變量進行篩選時，未探究減少變量數量對優化效果的影響，也未充分考慮變量之間的相互關系。在后續研究中會增加對相應問題的思考。

(3)文中對車門進行的多學科性能分析還不夠全面，希望在后續的研究中能夠更加全面、更加深入考慮其多學科性能，并與實際的試驗相結合。