基于氣門彈簧設計關鍵參數的計算與校核

孫輝國，韋靜思，呂偉，梁明曦，占文鋒

(廣州汽車集團股份有限公司汽車工程研究院，廣東廣州 511434)

0 引言

氣門彈簧是發動機配氣機構最重要的零部件之一，是保證氣門及整個配氣機構能夠平穩運行的關鍵零部件。在凸輪運行在基圓部分時，保證氣門與氣門座圈密封緊閉，不發生二次開啟；在凸輪運行在開啟部分時，確保凸輪與從動件之間不發生脫離；在氣門落座瞬間，保證氣門不發生過大沖擊。因此氣門彈簧力不宜過小也不宜過大，所以氣門彈簧關鍵參數的選擇對發動機配氣平穩運行是至關重要的[1-2]。

本文作者通過大量的經驗和總結，明確了氣門彈簧關鍵參數(F1、F2和工作段平均剛度k)的計算公式及流程。基于廣汽某款發動機氣門彈簧的選型，在設計早期正向確定能夠滿足配氣機構穩定運行的氣門彈簧。并通過配氣機構運動學與動力學分析，證明文中提到的氣門彈簧選型的方法和流程簡便高效，值得推廣。

1 氣門彈簧相關參數的確定

1.1 氣門彈簧預緊力F1的計算

當氣門動作在凸輪基圓階段時，此時氣門是關閉的。氣缸內的氣體壓力較大，對氣門密封有利，但是如果氣道內氣體壓力大于氣缸內的氣體壓力，氣門兩邊的壓力差會使關閉的氣門打開，即在發動機壓縮和膨脹行程時出現氣門關不嚴的情況。為了避免這樣的情況發生，氣門彈簧殘余力(Frs)應該滿足以下要求：

Frs=F1×0.85-Fa-Fb-Fc-Fd>30 N

(1)

式中：Frs為氣門彈簧殘余力，N；

Fa為氣門兩側氣體的壓力差，N；

Fb為氣道壓力循環波動的力，N；

Fc為氣門受液壓挺柱的頂開力，N；

Fd為氣門反彈時約10g的慣性力，N；

F1×0.85為考慮彈簧的公差以及顫振,取F1的85%。

(1)Fa為氣門兩側氣體的壓力差[3]，計算公式為

(2)

式中：pp為氣道壓力，MPa；

pc為缸內壓力，MPa；

Dv為氣門密封面直徑，mm；

Ds為氣門桿直徑，mm。

(2)Fb為考慮氣道壓力循環波動對氣門壓力的影響，其中氣道壓力波動值Δp=0.05～0.1 MPa，計算公式為：

(3)

(3)Fc為氣門受液壓挺柱內油壓的頂開力，計算公式為

Fc=Fhlif·Lcam/Lvalve

(4)

式中：Fhlif為油壓對挺柱柱塞的推力，N；

Lcam為凸輪側搖臂力臂長度，mm；

Lvalve為氣門側搖臂力臂長度，mm。

(4)Fd為氣門反彈時閥面受到的約10g的慣性力，計算公式為

Fd=10×9.8×M

(5)

式中:M為閥系的運動總質量，其計算公式為

(6)

式中：mv為氣門質量，kg；

mc為氣門上座質量，kg；

ml為氣門鎖片質量，kg；

ms為氣門彈簧質量，kg；

If為搖臂轉動慣量，kg·m2；

Lf為搖臂支撐點到氣門中心線的距離，m。

按照以上公式分別確定Fa、Fb、Fc和Fd，由Frs>30 N可以得到F1的理論最小值,這個理論最小值可以確保凸輪運行在基圓部分時，氣門與氣門座圈密封緊閉，不發生二次開啟。

1.2 氣門最大升程彈簧力F2的計算

一般當氣門升程最大時，負加速度絕對值最大，此時氣門彈簧力F2需要克服閥系運動質量的慣性力，避免出現搖臂滾子與凸輪飛脫的情況，同時考慮一定量的彈簧安全系數t=1.1～1.8，即氣門最大升程彈簧力F2的公式為：

F2>M·a·t

(7)

式中：t為彈簧安全系數；

a為氣門最大負加速度絕對值，m/s2，如圖1所示。

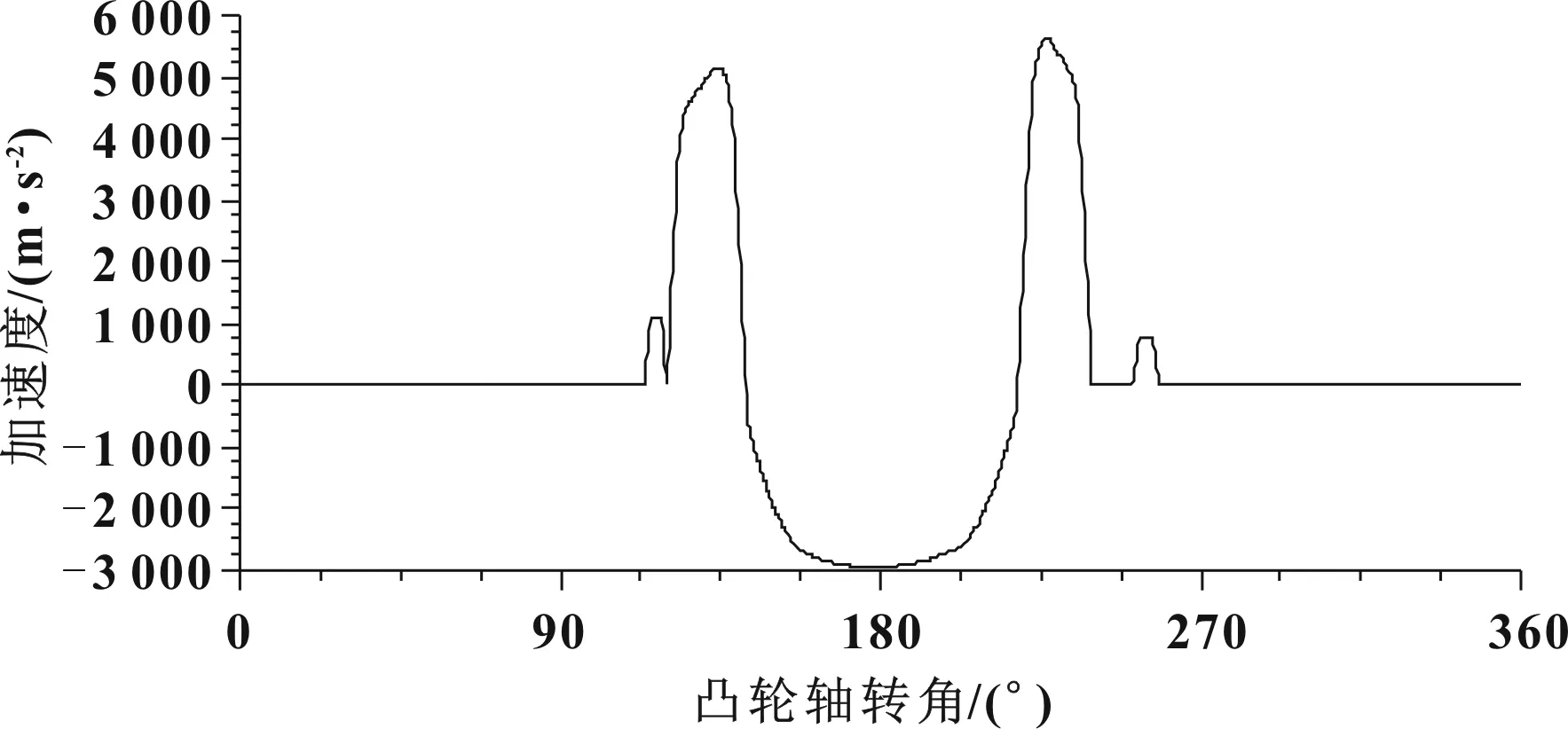
圖1 氣門加速度曲線

1.3 氣門彈簧工作段平均剛度k的計算

公式(1)和(7)確定了氣門彈簧的F1和F2，則氣門彈簧工作段的平均剛度k的計算公式為

k=(F1-F2)/Sh

(8)

式中：Sh為氣門開啟最大升程，mm。

1.4 對于F1不宜過小的補充說明

如果F1過小，則會使氣門彈簧工作段的平均剛度太大，導致彈簧設計困難。同時F1過小，在氣門開啟初期，彈簧力過小無法克服氣門的慣性力，導致凸輪與從動件發生飛脫現象。

2 氣門彈簧的選型計算

文中基于廣汽某款機型運用以上計算公式進行氣門彈簧的選型計算。以驗證公式使用的可行性。表1為計算需要輸入的數據。

表1 氣門彈簧選型計算輸入

根據公式(1)，可以得到F1>150 N;根據公式(7)，可以得到F2>440 N;根據公式(8)，可以得到氣門彈簧工作段平均剛度k=30.7 N/mm。氣門彈簧供應商按照F1和F2的要求，提供氣門彈簧成品。彈簧的具體參數為：F1=260 N，F2=488 N，工作段平均剛度k=46 N/mm。

3 氣門彈簧校核計算流程

圖2為氣門彈簧校核計算的流程，按照計算流程，通過以上公式可以一次確定配氣機構需要的氣門彈簧關鍵參數F1、F2和工作段平均剛度k，彈簧供應商按照要求的彈簧參數設計氣門彈簧。這樣大大減少了仿真和設計來回校核的工作量，提高了工作效率。

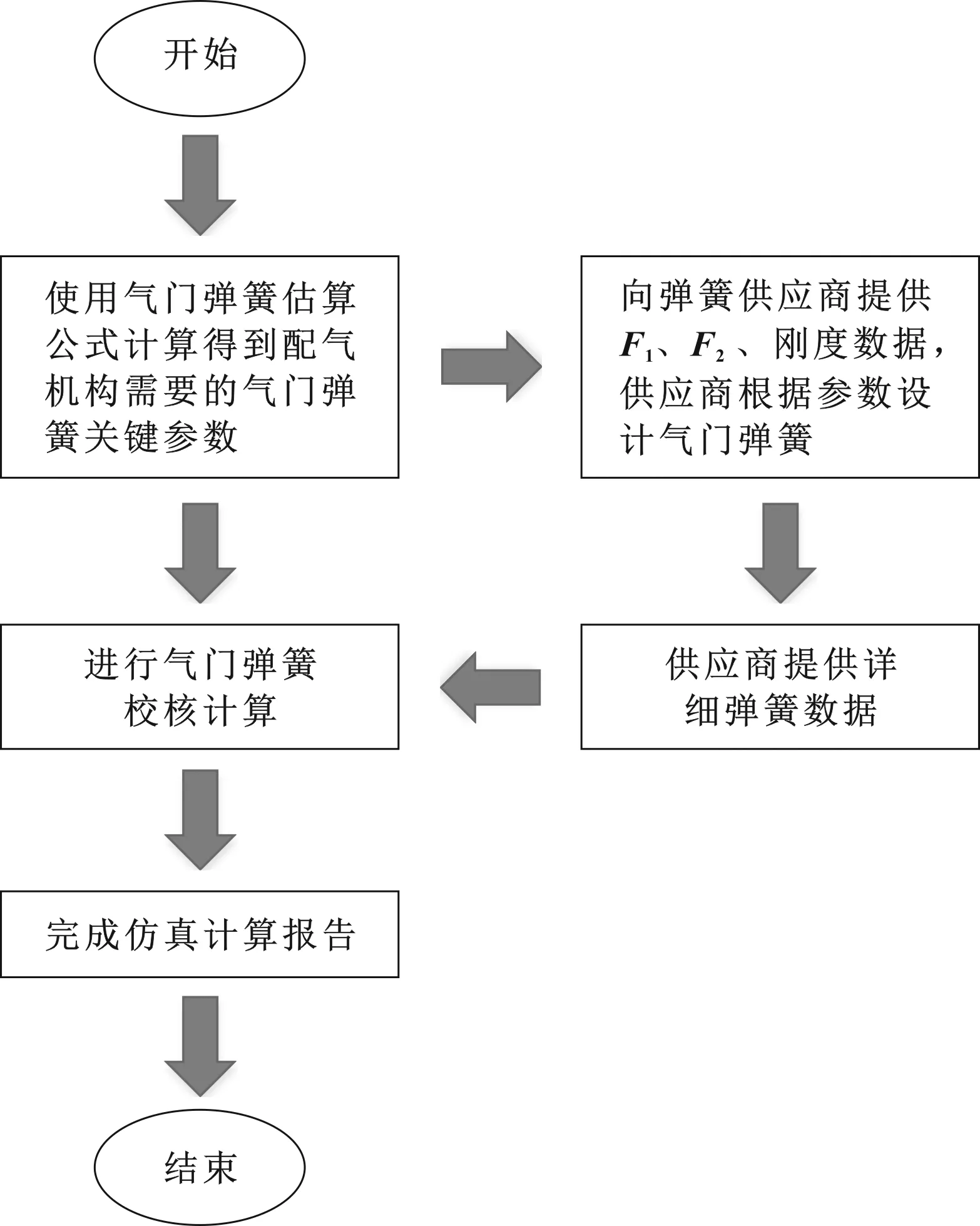
圖2 氣門彈簧校核計算流程

4 氣門彈簧校核計算

氣門彈簧對于配氣機構至關重要，對于整個配氣機構的運動學和動力學結果都將產生較大的影響。因此需要對氣門彈簧做更加詳細的運動學和動力學分析，以考察氣門彈簧是否滿足整個配氣機構的要求[4]。該發動機配氣機構為典型的指型搖臂結構。文中應用AVL-EXCITE軟件來進行配氣機構的運動學和動力學分析，分析氣門彈簧是否能滿足配氣機構的仿真評價標準。通過AVL-EXCITE軟件建立的單閥系分析模型如圖3所示。

圖3 AVL-EXCITE建立的單閥系模型

4.1 運動學分析結果

(1)凸輪和從動件是兩個具有曲面的彈性體，在傳遞載荷時，就形成了一個接觸的區域，并伴隨著產生了接觸應力。如果凸輪和從動件之間的接觸應力太大，在周期性接觸應力的反復作用下，將引起凸輪或者從動件工作表面的較大損壞。從計算結果圖4來看，凸輪和從動件的接觸應力小于1 100 N/mm2，低于設計要求的最大許用應力[4]。

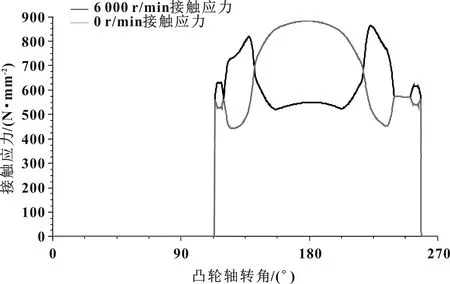
圖4 凸輪與從動件接觸應力結果

(2)在配氣機構運動學分析中，氣門彈簧裕度是氣門彈簧力與從動件慣性力的比值。氣門彈簧力要保證有一定的余量，否則從動件將從凸輪表面跳開，發生“飛脫”現象。但是也不能太大，否則產生過大的摩擦功，影響發動機的性能。從計算結果圖5來看，氣門彈簧的安全裕度大于t，配氣機構不會發生飛脫現象[2]。

圖5 氣門彈簧安全裕度

(3)為了防止搖臂在運動中從液壓挺柱球頭脫落，配氣機構要求搖臂對液壓挺柱軸向力大于100 N、液壓挺柱軸線垂直方向力小于600 N。從計算結果圖6來看，液壓挺柱軸向和垂直方向的力均滿足要求，搖臂不會從液壓挺柱球頭脫落[5]。

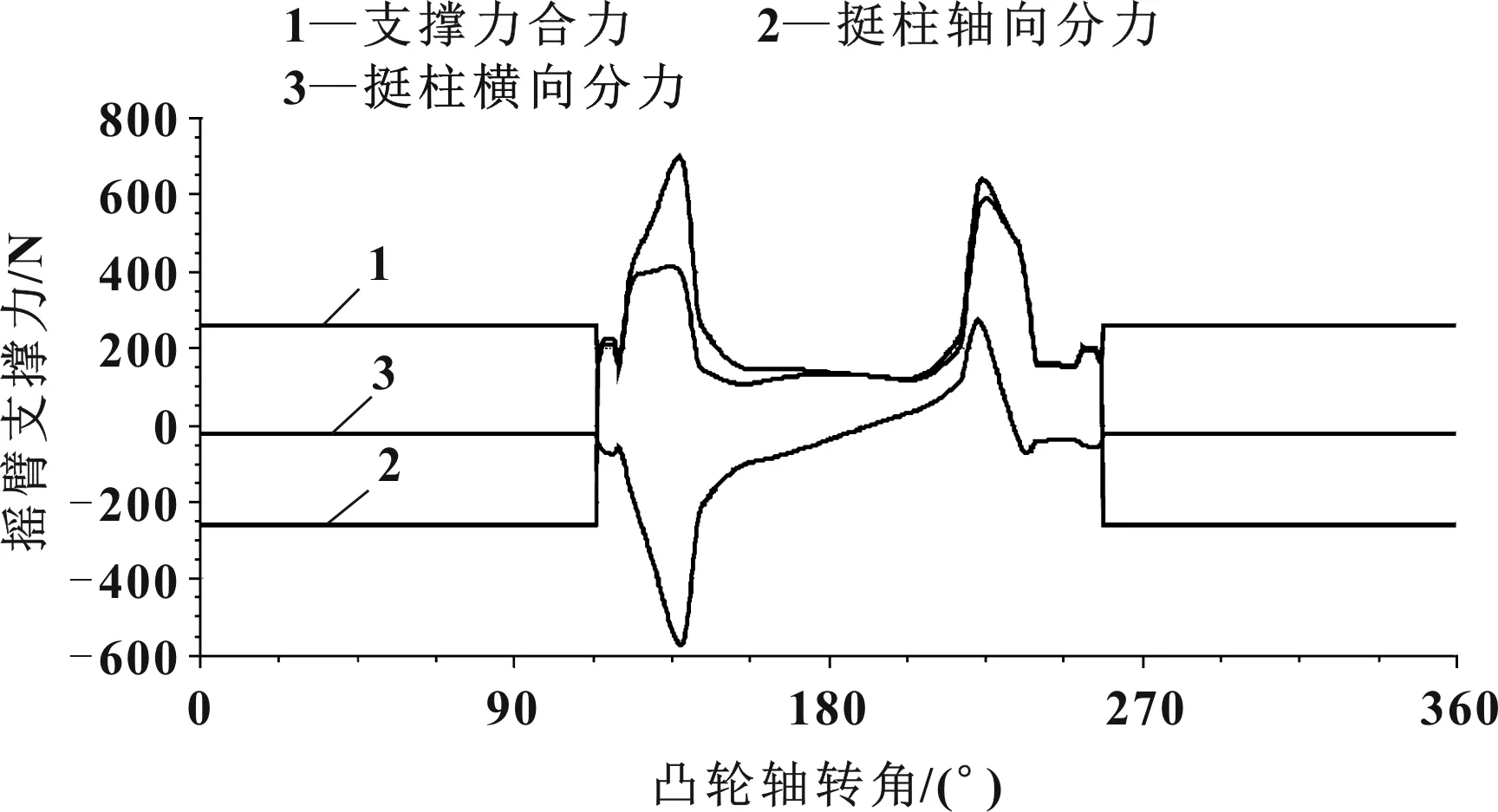
圖6 液壓挺柱受力結果

(4)由于氣門桿頭部與搖臂之間是相對滑動的往復周期運動，當兩者之間的相對滑動速度過大，同時兩者之間的接觸應力過大時，則會出現氣門桿頭部快速磨損的情況。配氣機構要求氣門桿頭部與搖臂相對速度下的接觸應力在閾值線以下。從計算結果圖7來看，氣門桿頭部與搖臂之間的相對運動不會引起氣門桿的快速磨損[5]。

圖7 氣門桿頭部與搖臂相對速度下接觸應力

4.2 動力學分析結果

(1)氣門落座的好壞對氣門座可靠工作影響很大，當氣門落座速度比較大時，會增加氣門閥面的磨損，同時產生較大的噪聲。圖8為氣門閥面的運動曲線，從計算結果來看，氣門閥面的落座速度小于1 m/s，配氣機構不會產生較大的噪聲[6]。

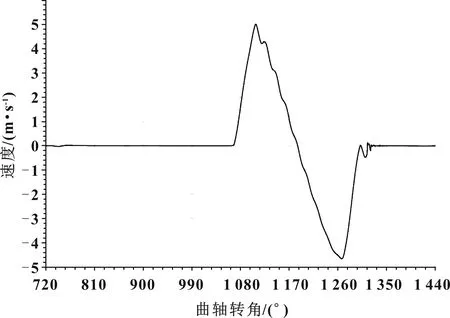
圖8 氣門運動速度

(2)氣門關閉時的落座力不應太大，否則會引起氣門反跳，導致氣門二次開啟。通常情況下要求氣門閥門落座力小于6倍彈簧預緊力。圖9為氣門閥面的落座力，從計算結果圖來看，氣門閥面的落座力小于6倍的彈簧預緊力，氣門不會發生反跳現象[6]。

圖9 氣門閥面受力

(3)圖10為凸輪與從動件之間的接觸力結果，從計算結果可以看到在凸輪工作段區域，未發生凸輪與從動件之間接觸力為0的情況，說明凸輪與從動件未發生飛脫現象[7-8]。

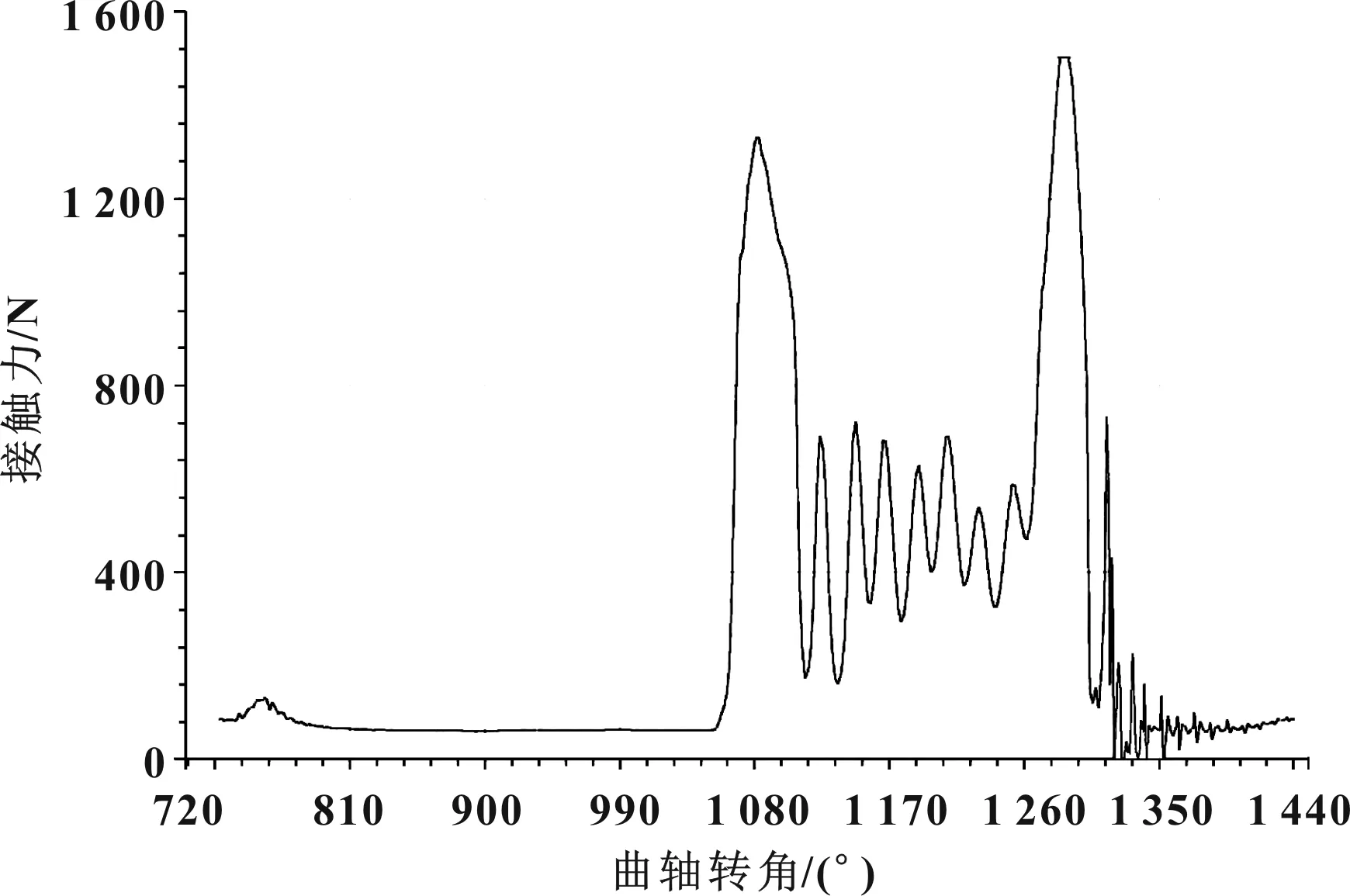
圖10 凸輪與從動件接觸力

(4)圖11為氣門彈簧各質量點的受力結果，從計算結果可以看到在凸輪工作段區域，未發生彈簧質量點受力突變的情況，說明彈簧未發生并圈現象。

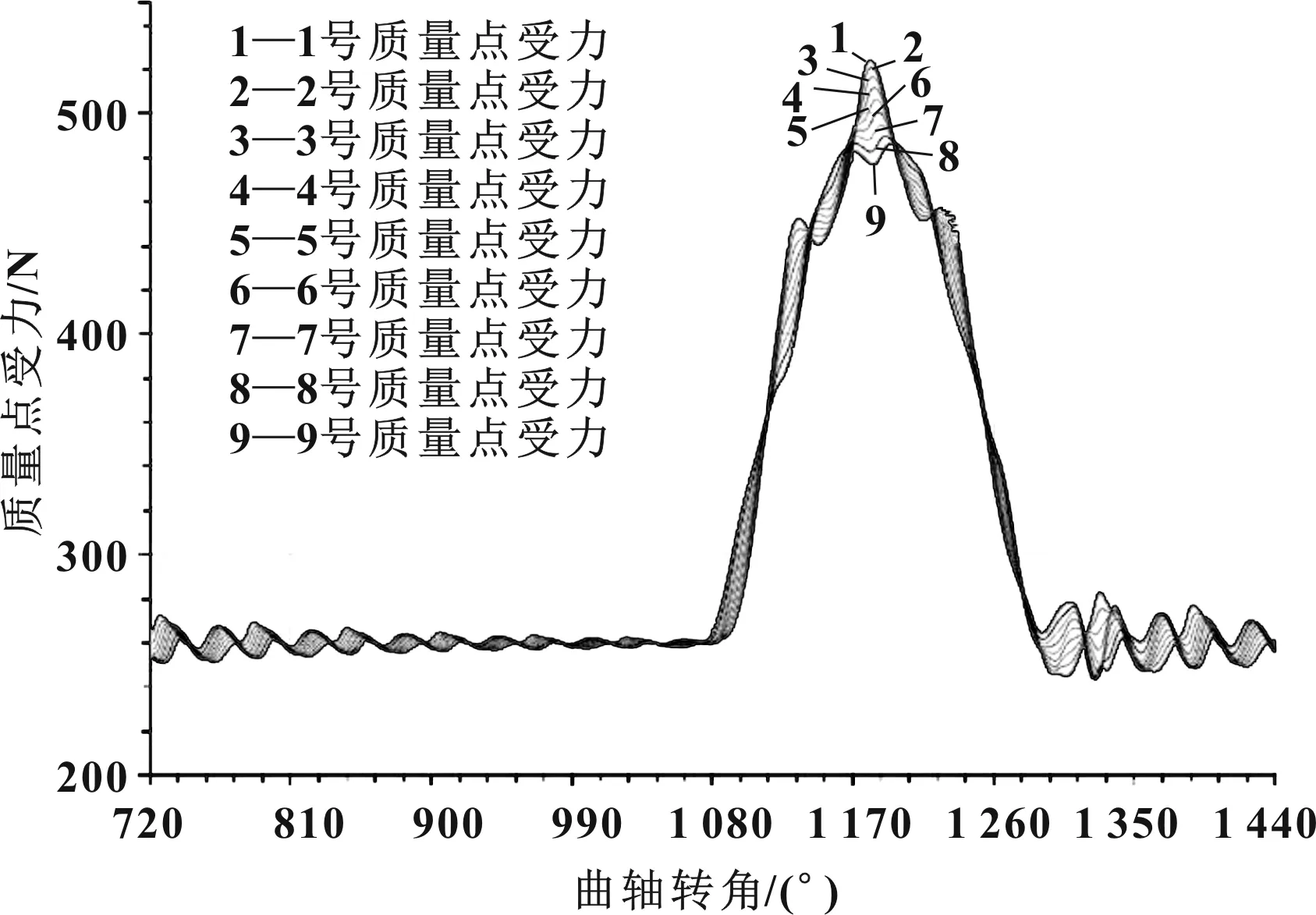
圖11 氣門彈簧各質量點受力

5 結束語

按照氣門彈簧校核計算的流程，通過理論計算以及運動學和動力學的分析，新的氣門彈簧符合配氣機構仿真的各項評價指標，氣門彈簧滿足發動機配氣機構穩定工作的需要。

通過氣門彈簧關鍵參數的確定，可以在配氣機構設計早期，快速地進行氣門彈簧的選型，減少了仿真和設計之間來回校核繁瑣的工作量，大大地提高了工作效率。文中提出的氣門彈簧選型的流程方法簡便易行，是一種值得推廣的高效的氣門彈簧選型方法。