新型電控空氣懸架系統集成控制策略研究*
馬英照,嚴天一,趙燕樂
(青島大學機電工程學院,青島266071)
前言
傳統被動懸架系統剛度、阻尼等主要參數不可實時調節,導致車輛平順性與操縱穩定性較差,同時在高速轉彎或緊急避讓等工況下易導致車輛側翻等危險事故。具有電機式主動橫向穩定器的新型電控空氣懸架系統可有效協調平順性與操縱穩定性之間的固有矛盾,有效提升整車綜合性能。
國內外學者已提出多種控制算法以提高空氣懸架性能,如:Moheyeldein等[1]通過搭建具有附加氣室的2自由度空氣懸架仿真模型,參數化仿真分析了附加氣室體積及其內部壓力等主要參數對懸架性能的影響規律。Kim等[2-4]分別提出電控空氣懸架系統閉環容錯控制算法和滑模控制算法,并通過仿真和實車試驗,驗證了所設計控制算法的有效性。嚴天一等[5]利用基于模型設計的方法,搭建電控空氣懸架系統控制策略,并設計其電子控制單元。江洪等[6-7]構建附加氣室容積可調空氣彈簧的整車懸架模糊控制算法,并開發出整車半主動空氣懸架的TS型神經模糊控制器。雖然電控空氣懸架可提高車輛平順性,但其存在側傾穩定性較差的技術問題,且傳統被動橫向穩定桿的扭轉剛度為常值,不能夠根據行駛工況適時調節電控空氣懸架系統的側傾剛度;而電機式主動橫向穩定器具有主動實時調整車輛側傾剛度且節能效果明顯等技術優點。Buma、Suzuki等[8-9]設計了基于三相無刷直流電機與諧波齒輪減速器的電機式主動橫向穩定器,與液壓式主動橫向穩定器相比,可有效降低燃油消耗。Sorniotti[10]設計并試制出一種電機式主動橫向穩定器,相關硬件在環試驗與實車試驗結果表明,可有效改善車輛側傾穩定性與操縱穩定性。周兵等[11]構建含主動懸架與主動橫向穩定桿的整車動力學模型,并綜合利用線性與PID控制提出集成控制策略。
針對電控空氣懸架與電機式主動橫向穩定器集成控制研究尚屬鮮見,并且基于傳統分布式架構的單獨控制方法,管理復雜、數據傳輸速率及處理效率較低,具有強大算力的并行多核域控制器將集成原來歸屬于各個獨立電子控制單元的大部分功能[12-16]。故本文中綜合考慮車輛平順性與抗側傾穩定性,提出對電控空氣懸架和電機式主動橫向穩定器實施集成式域控制,通過搭建電控空氣懸架系統整車動力學模型與電機式主動橫向穩定器模型,提出新型電控空氣懸架系統集成控制策略,開發其并行多核電子控制單元,開展相應的典型工況離線仿真與硬件在環試驗以有效評估新型控制策略主要性能。
1 系統模型構建
1.1 電控空氣懸架系統整車動力學模型
9自由度電控空氣懸架系統整車動力學模型由車身的垂向運動、側向運動、俯仰運動、側傾運動、橫擺運動及車輪垂向運動等子模型組成[17](圖1~圖3)。
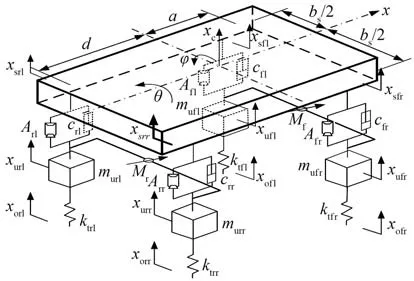
圖1 電控空氣懸架系統整車動力學模型

圖2 側向、橫擺模型
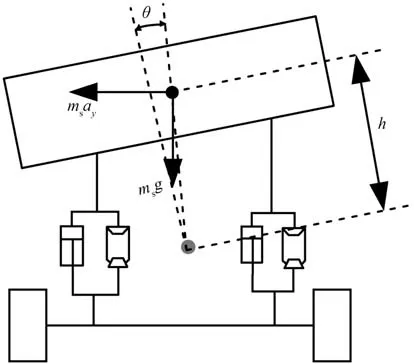
圖3 側傾模型
垂向運動模型:
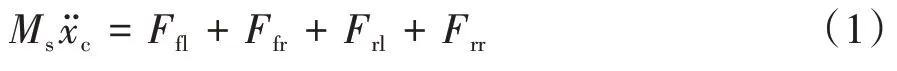
側向運動模型:
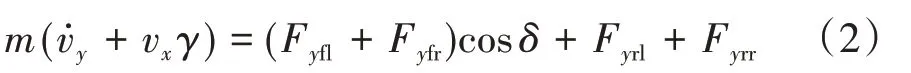
俯仰運動模型:
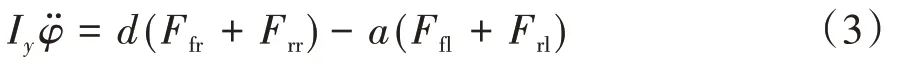
側傾運動模型:
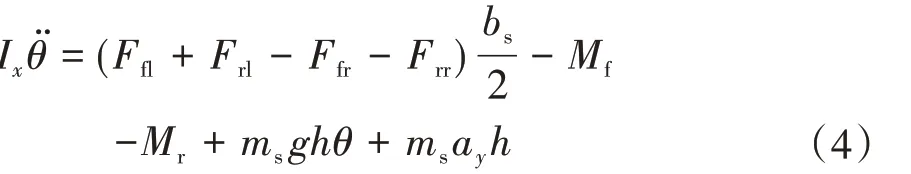
橫擺運動模型:
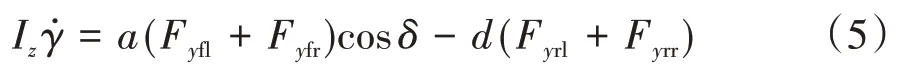
非簧載質量運動模型:

其中:
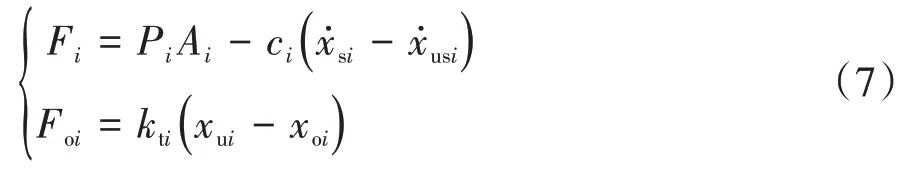
當車身俯仰角θ和側傾角φ在較小范圍內變化時,車身質心的垂直位移與四車輪處車身的垂直位移存在如下關系:
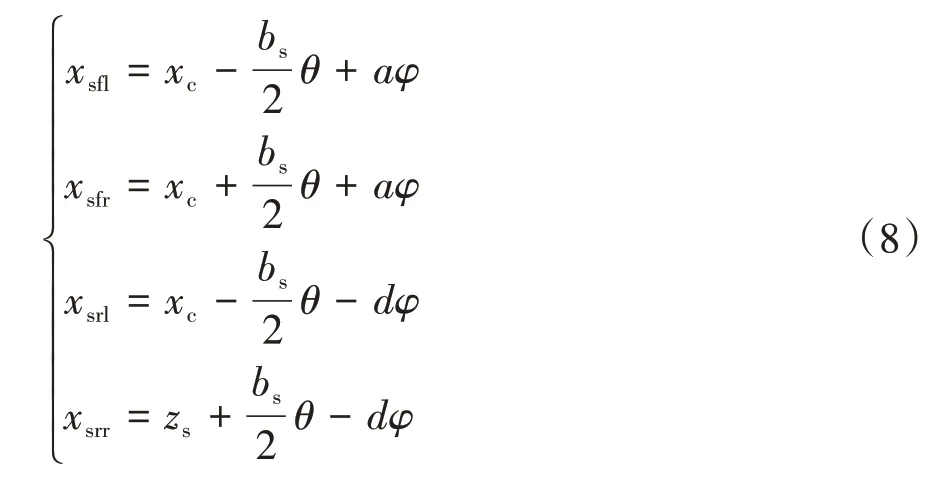
式中:m為整車質量;ms為簧上質量;mui(i=fl、fr、rl、rr)為簧下質量;θ為車身側傾角;φ為車身俯仰角;γ為橫擺角;δ為前輪轉角;Ix、Iy、Iz為車身側傾、俯仰、橫擺轉動慣量;a、d為車輛質心至前、后軸的距離;bs為輪距;h為車身側傾半徑;xc為簧上質量質心位移;xsi為各懸架處簧上質量位移;xui為各簧下質量位移;Mf、Mr分別為前、后主動橫向穩定器控制轉矩;ki為各懸架處彈簧剛度;ci為各懸架處減振器阻尼;Fi為懸架對車身的垂向力;Foi為車輪動載;xoi為路面不平度激勵;kti為各輪胎剛度;Fyi為車輪側向力;vx為質心縱向速度;vy為質心側向速度;pi為空氣彈簧內氣體壓力;Ai為空氣彈簧有效面積。
1.2 空氣彈簧模型
假定空氣彈簧充放氣過程為變容積絕熱過程,則空氣彈簧充放氣變質量模型:
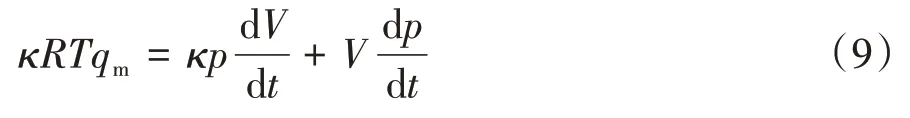
在車身高度調節過程中,將空氣彈簧模型視為活塞缸模型,即假定空氣彈簧容積變化近似看為固定容積變化率下的彈簧垂直位移變化:

聯立式(9)和式(10),推導出完整空氣彈簧充放氣過程理論模型:
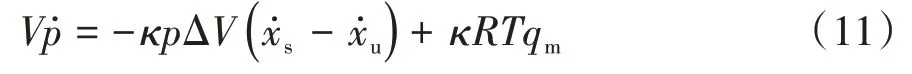
式中:κ為空氣絕熱系數;R為氣體常量系數;T為空氣彈簧內部溫度;p為空氣彈簧內部氣體壓力;V為空氣彈簧內部氣體體積;V0為空氣彈簧初始容積;ΔV為空氣彈簧有效容積隨高度的變化率;qm為空氣彈簧充放氣時氣體質量流量。
1.3 輪胎模型
為合理表征輪胎在轉向工況下的力學特性,采用“魔術公式”輪胎側向力學模型計算輪胎側偏力。在不考慮車輪外傾角條件下,即外傾角γt=0,水平方向偏移Sh=0,垂直方向偏移Sv=0,則該輪胎模型如式(12)所示[18],其擬合系數值見表1。
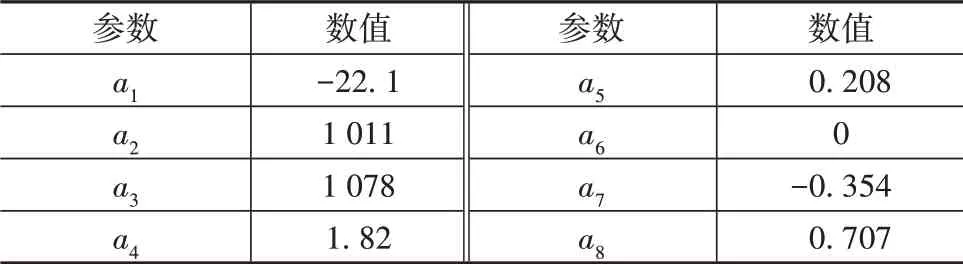
表1 輪胎側向力學模型擬合系數
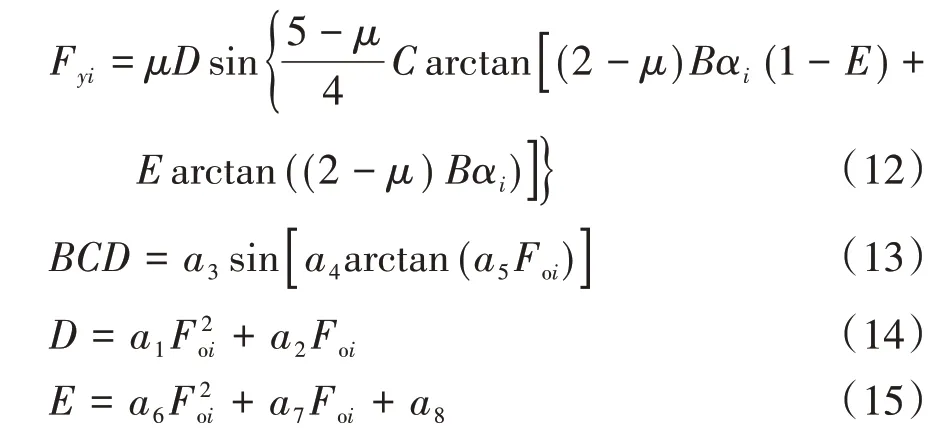
式中:Fyi為車輪側向力;μ為路面附著系數;αi為輪胎側偏角;B、C、D、E分別為車輪側向力一側偏角曲線峰值因子、形狀因子、剛度因子和曲率因子;Foi為車輪動載。
1.4 路面模型
本文采用非平穩時域路面模型[19]:

式中:xoi為輪胎i(i=fl、fr、rl、rr)處路面不平度;x1、x2為系統狀態變量;f0為下截止頻率,取0.01 Hz;v為車速;n0為標準空間頻率,取0.1 m-1;G0為路面不平度系數;ω(t)為高斯白噪聲,均值為0;d為輪距;l為軸距。
1.5 電機式主動橫向穩定器模型
本文中所述電機式主動橫向穩定器采用三相無刷直流電機作為作動器,其內嵌電機通電以后產生的電磁轉矩經諧波齒輪減速器減速增扭作用后,傳遞到左、右橫向穩定桿臂,產生作用于車身的垂向力,并形成反側傾力矩,以抑制整車側傾運動(圖4和圖5)。
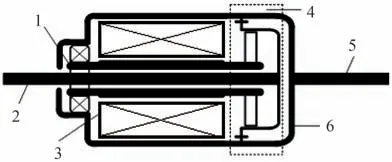
圖4 電機式主動橫向穩定器結構示意圖
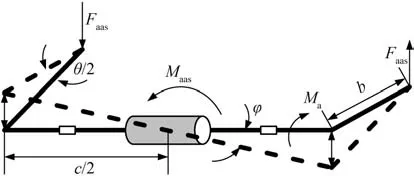
圖5 主動橫向穩定器受力分析圖
內嵌電機輸出轉矩與反側傾力矩之間存在如下關系:

式中:Faas為主動橫向穩定器作用于整車底盤的垂向力;Ma為主動橫向穩定器輸出轉矩;Maas為主動橫向穩定器產生的反側傾力矩;b為左、右橫向穩定桿縱臂長度;c為主動橫向穩定器的長度;θe為左、右橫向穩定桿臂相對轉角;θe∕2為穩定桿臂與水平方向夾角。
1.6 三相無刷直流電機模型
電機式主動橫向穩定器內嵌電機的定子繞組采用星形聯接,則繞組相電流之間滿足關系式:

三相電壓方程:
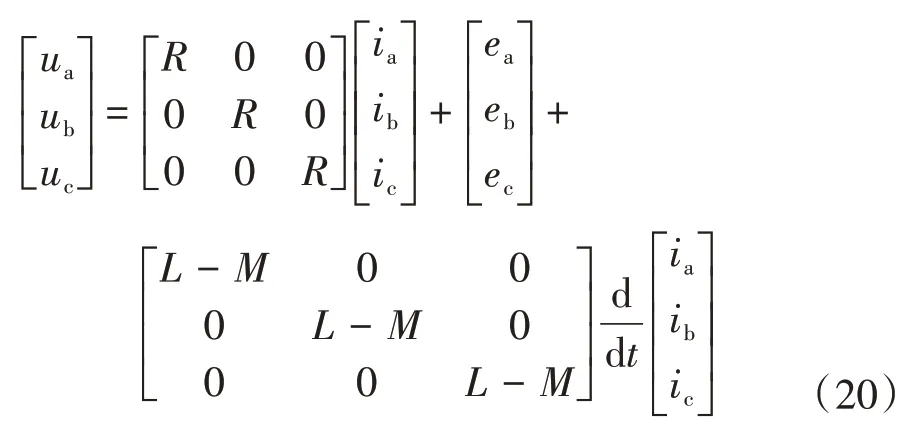
內嵌電機輸出電磁轉矩方程:
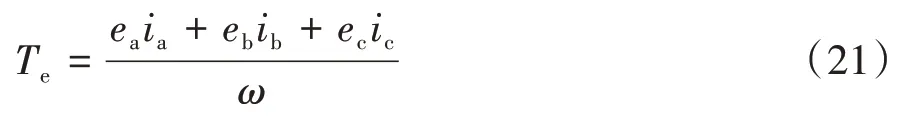
內嵌電機轉子運動方程:

電機式主動橫向穩定器輸出轉矩:

式中:ua、ub、uc為定子繞組各相電壓;ia、ib、ic為定子繞組各相電流;L、M為定子繞組的自感和互感系數;R為定子繞組阻值;ea、eb、ec為定子繞組相反電動勢;Tl為負載轉矩;J為電機轉動慣量;B為阻尼系數;ω為電機角速度;i為諧波齒輪減速比。
2 集成控制策略設計
將車身側傾角作為主要優化指標,通過電控空氣懸架系統降低車身質心高度與電機式主動橫向穩定器輸出的反側傾力矩,以提高車輛操縱穩定性與抗側傾性能,新型集成控制策略具體如圖6所示。
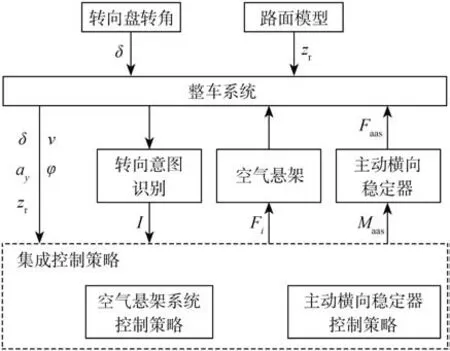
圖6 集成控制策略框圖
空氣彈簧充放氣系統存在時滯,且轉向工況下不宜進行懸架高度切換,因此本文采用文獻[20]中提出的轉向意圖辨識算法進行駕駛意圖I識別。
2.1 空氣懸架系統控制策略設計
本文中利用Matlab∕Stateflow搭建空氣懸架控制策略模型,具體控制邏輯如圖7所示:電子控制單元通過實時處理車速、路況、車身高度以及儲氣筒壓力等信號,控制懸架高度在高位、標準和低位等3種不同模式之間進行適時切換。圖7中各控制邏輯值具體如表2所示。
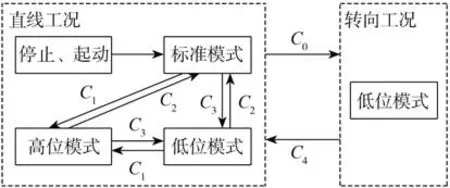
圖7 空氣懸架系統控制策略框圖
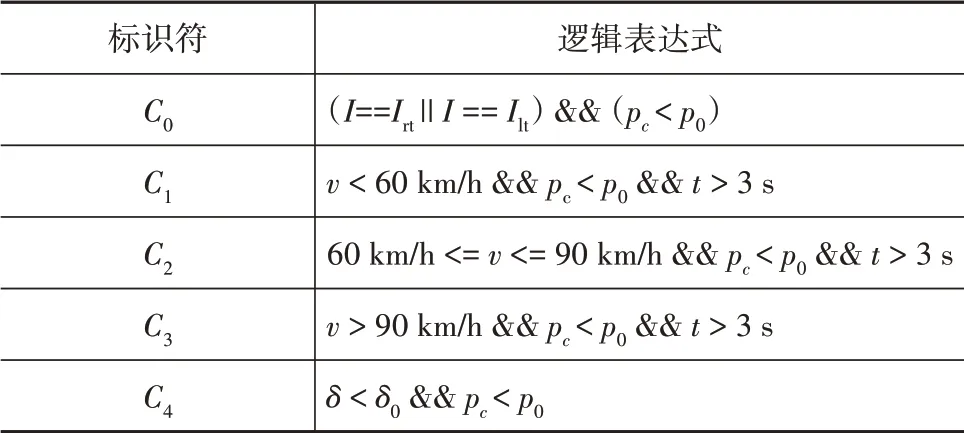
表2 不同模式控制邏輯值
根據轉向意圖辨識算法,若行駛意圖I為右轉彎Irt或左轉彎Ilt,則判定車輛即將進入轉向工況,且儲氣筒壓力pc小于所標定壓力閾值p0時,懸架提前切換到低位模式;若前輪轉角δ小于所標定轉角閾值δ0,則判定此時車輛處于直線工況,懸架高度進入下述3種模式之一:
(1)當車速v>90 km∕h、pc<p0且持續時間超過3 s時,懸架切換到低位模式;
(2)當車輛停止、起動或車速60 km∕h≤v≤90 km∕h、pc<p0且持續時間超過3 s時,懸架切換到標準模式;
(3)當車速v<60 km∕h、pc<p0且持續時間超過3 s時,懸架切換至高位模式。
2.2 主動橫向穩定器控制策略設計
當設置車輛目標側傾角時,既要保證車輛具有較小的側傾角[11],亦需考慮駕駛員的主觀感受,以獲得良好路感,則目標側傾角與車身側向加速度關系[21]如式(24)所示。
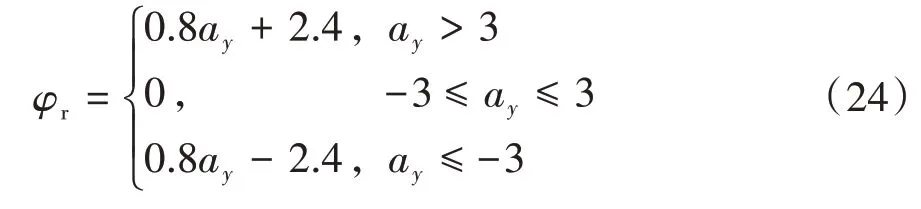
通過三次插值擬合可得到式(25),其擬合曲線如圖8所示。
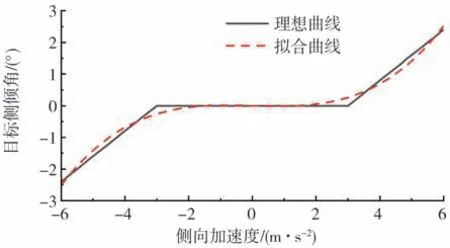
圖8 目標側傾角與側向加速度關系曲線
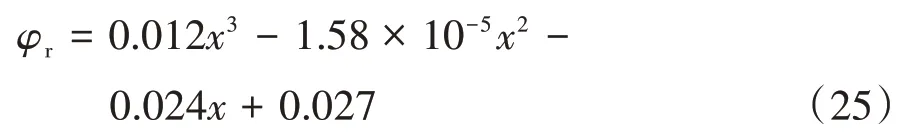
傳統被動橫向穩定桿所提供的反側傾力矩與車身側傾角呈線性關系[22],主動橫向穩定器輸出的反側傾力矩與車身側傾角、車輛側向加速度等信息有關,據此提出主動橫向穩定器控制策略(圖9)。首先,線性控制器模擬被動橫向穩定桿作用,通過整車模型輸出的側傾角得出線性反側傾力矩,保證主動橫向穩定器具有較好的響應速度;然后PID控制器通過實際側傾角與目標側傾角值差值計算得到補償力矩,彌補主動橫向穩定器輸出中的非線性部分,使得車身側傾角符合目標側傾角—側向加速度關系曲線;最后將二者相互疊加得到車輛所需的反側傾力矩。
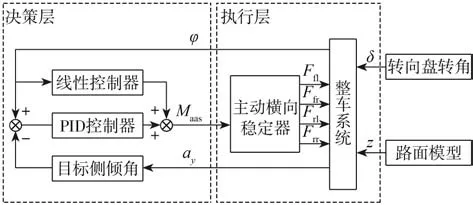
圖9 主動橫向穩定器控制策略框圖
3 仿真分析
為驗證集成控制策略的有效性,并分析新型電控空氣懸架系統對整車性能影響效果,選取轉向盤角階躍輸入及雙移線工況作為試驗工況,以車身側傾角作為評價指標,利用Matlab∕Simulink和Stateflow搭建電控空氣懸架系統整車動力學模型、電機式主動橫向穩定器模型以及新型電控空氣懸架系統控制策略模型,并利用典型試驗工況進行離線仿真分析,相關整車主要參數見表3。

表3 整車主要參數
轉向盤角階躍輸入仿真條件為B級路面,試驗車速為80 km∕h,經過0.2 s使前輪轉角轉動30°后保持穩定,且此過程車速保持不變(圖10);雙移線輸入仿真條件亦為B級路面,試驗車速同為80 km∕h,設定車輛行駛路線如圖11所示。

圖10 轉向盤角階躍輸入工況設計曲線

圖11 雙移線工況設計曲線
電控空氣懸架系統通常具有高位、標準、低位3種不同工作模式,因此分別在不同工作模式下對上述2種工況進行仿真,相關結果如圖12所示:在轉向盤角階躍工況下,標準模式車身側傾角穩態值比高位模式降低約8.9%,低位模式車身側傾角穩態值比標準模式降低約3.9%;在雙移線仿真工況下,標準模式車身側傾角穩態值比于高位模式最大值降低約9.7%,低位模式車身側傾角穩態值比于標準模式最大值降低約4.3%,發現通過改變車身高度可降低車身側傾角,提高抗側傾閾值,有效改善車輛操縱穩定性和抗側傾性能。
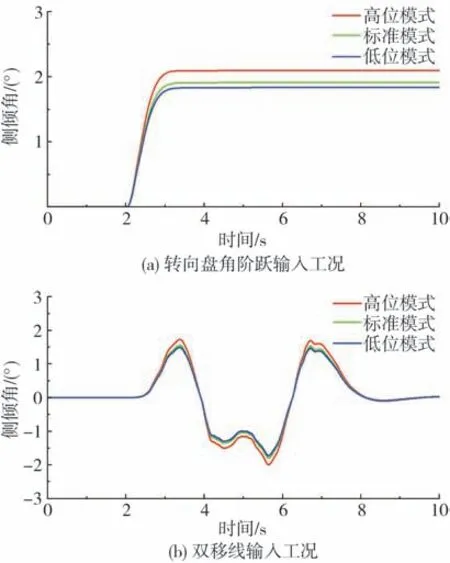
圖12 不同車身高度模式整車側傾角對比圖
采用集成控制策略的新型電控空氣懸架系統車身側傾角變化過程更加平緩。在轉向角階躍工況下,車身側傾角比無主動橫向穩定器控制的車身側傾角降低約50.7%,在雙移線工況下,車身側傾角降低約69.4%(圖13),并且與線性控制或PID控制單獨作用于主動橫向穩定器相比,集成控制的車身實際側傾角可快速趨近于目標側傾角,對其具有更好的跟隨性,控制效果更好。
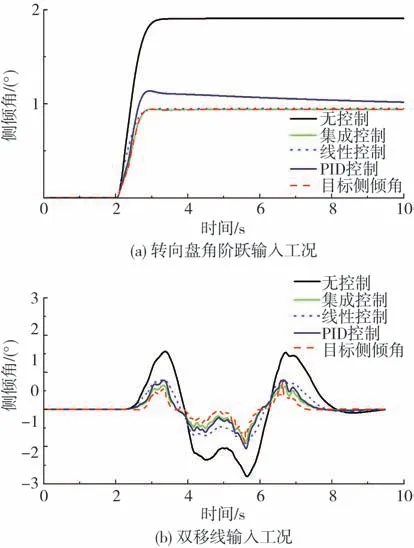
圖13 不同控制策略整車側傾角對比圖
4 硬件在環試驗
為進一步驗證新型電控空氣懸架系統集成控制策略,并測試新型電控空氣懸架系統并行多核電子控制單主要技術性能,本文基于Simulink∕Desktop Realtime實時仿真環境,利用并行多核電子控制單元與Kvaser Leaf Light V2 CAN總線分析儀等搭建硬件在環試驗平臺,并通過Embedded Coder代碼自動生成工具將電控空氣懸架系統與主動橫向穩定器系統控制策略模型轉化為可執行的C代碼,分別布置于微控制器內核0與內核1內,實現并行多核運行模式,以提高程序執行效率。硬件在環試驗框架如圖14所示。
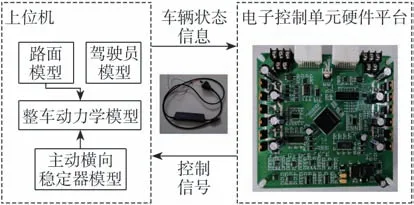
圖14 硬件在環試驗框架
利用與離線仿真相同工況,開展新型控制策略硬件在環試驗,并將其試驗結果與離線仿真結果進行比較分析(圖15),可知在轉向盤角階躍工況下,硬件在環仿真試驗數據的車身側傾角穩態值與離線仿真數據接近,約為0.94°;在雙移線工況下,硬件在環仿真試驗與仿真數據變化過程趨于一致,但中后期有小幅波動。上述硬件在環試驗結果表明,新型電控空氣懸架系統集成控制策略可有效地控制車身側傾角,改善車輛抗側傾性能。

圖15 硬件在環試驗與離線仿真結果對比
5 結論
(1)在轉向盤角階躍工況與雙移線工況下,利用Matlab∕Simulink搭建整車動力學集成仿真模型,對空氣懸架不同工作模式以及新型電控空氣懸架系統不同控制策略進行仿真。相關結果表明,所提出的新型電控空氣懸架系統集成控制策略可有效減小車身側傾角,并對目標側傾角具有較好的跟隨性。
(2)通過搭建的硬件在環試驗平臺,對比分析硬件在環試驗結果與離線仿真結果,進一步驗證了新型電控空氣懸架系統集成控制策略及其并行多核電子控制單元,并確認其可提高整車抗側傾性能。

