旋流器內兩種非牛頓流體的流動行為分析
鄧鑫,謝超,馬強,張進
(中國石油天然氣管道工程有限公司,河北 廊坊 065000)
水力旋流器是鉆井液固控系統的重要組成部分,根據離心沉降原理實現兩相或多相分離[1-3]。含固相顆粒的料液在一定壓力或速度下切向引入旋流器,產生強烈的旋轉運動,在離心力作用下,顆粒相產生沿固體壁面的外旋流運動,但是由于徑向流體曳力的阻礙,不同性質的顆粒沿旋流器徑向方向重新分布,密度小或粒度細的顆粒隨流體遷移至內旋流器經溢流口排出;而密度大、粒度粗的顆粒借助較大的離心力由底流口收集,達到分離或分級目的[4-5]。
CHU[6]采用CFD-DEM(離散元分析方法)分析了旋流器內顆粒在水中的運動軌跡以及受力。MOGNON[7]以水為流體介質,通過添加黏性添加劑來代替鉆井液,分析了隨黏度變化旋流器中細微顆粒的分離過程。MARTHINUSSEN[8]實驗研究了水力旋流器中高黏度液體顆粒的分離性能,用于指導水力旋流器幾何形狀的改進,使其更適合黏性流體。艾志久[9]用冪律流體與水描述鉆井液,通過CFD 數值模擬方法分析了兩種流體在旋流器內旋流特性的差異。結果顯示冪律流的靜壓、軸向速度及徑向速度均大于水,并且零軸速包絡面(The locus of the zero axial velocity vectors,簡稱LZVV)更靠近壁面,但切向速度顯示冪律流體要小于水。
鉆井液是屬于賓漢模式與冪律模式間的一種非牛頓流體,在模擬水力旋流器兩相分離時,使用傳統流變參數模式描述鉆井液,在全剪切速率下并不能保證準確性[10]。樊洪海[11-12]提出一種新型四參數鉆井液模式,能滿足各種剪切速率下對鉆井液流變行為的描述。劉洪斌[13]分別使用四參數流體、冪律流體、水作為流體介質,通過CFD數值模擬方法對比分析了流體的旋流特性,得出非牛頓流體的靜壓力與軸向速度要大于牛頓流體,切向速度要小于牛頓流體;四參數流體靜壓與切向速度均小于冪律流體。
本文采用同種鉆井液的兩種表達方式——四參數模式和冪律模式,結合雷諾應力模型(Reynolds Stress Model, 簡稱RSM),對比分析兩種非牛頓流體鉆井液在水力旋流器內的旋流動行為以及差異的分布情況。
1 數值模擬方法
1.1 物理模型以及網格劃分
在HSIEH[14]模型基礎上改進模型,按比例尺為1∶1 建立雙進料口模型[15],入口截面形狀為矩形,如圖1 所示。兩個進料口保持進料速度相同。建模坐標原點位于旋流器頂蓋圓心處,水力旋流器截面尺寸視圖如圖2 所示,尺寸信息如表1 所示。使用ICEM 劃分結構網格,共計23.5 萬網格單元,如圖3 所示。通過多次計算,發現進一步增加網格單元數時,并不能提高計算結果的準確性。根據HSIEH實驗條件,采用相同邊界條件驗證物理模型以及計算模型。HSIEH 質量流量為66.99 kg·min-1,換算為速度入口,可得本模型入口速度為2.23 m·s-1。與HSIEH 切向速度實驗數據對比,發現除了在極大值位置偏低外,其他各個位置速度吻合良好,如圖4所示,與唐波[16]驗證所得結果類似。

圖1 水力旋流器ZY 截面

表1 水力旋流器截面尺寸

圖2 模型網格

圖3 切向速度計算值與測量值對比
1.2 四參數模式鉆井液

式中:τ—切應力,Pa;
τo—屈服應力,Pa;
a—黏度系數,Pa·s;
γ—剪切速率,s-1;
b—稠度系數,Pa·sn;
n—流性指數,無因次。
選用1 組水泥漿的黏度計讀數,通過回歸算法,分別得到冪律模式與四參數模式的流變參數[17],如表2 所示。模擬鉆井液在水力旋流器內旋流作業時,分別采用四參數模式和冪律模式作為流體介質,其中四參數模式鉆井液流變參數采用用戶自定義功能編譯。

表2 流變參數計算結果
1.3 計算模型及邊界條件
RSM 模型在對雷諾應力的計算過程中,盡可能全面地考慮了可能引起雷諾應力變化的各種因素。其中的壓力場和流體旋轉引起的應力產生項和系統旋轉產生項尤為重要,水力旋流器工作過程中,流體進入旋流器后,在很小的空間內做高速旋轉運動,其壓力梯度、切向速度梯度都很大,所以壓力梯度和流體旋轉對雷諾應力的影響不能忽略。相比于k-ε模型、RNGk-ε模型更適合模擬水力旋流器內的流場運動。
設置入口速度為10 m·s-1,從入口方向垂直進料。根據旋流器實際工作情況,出口邊界條件均設大氣壓,空氣回流指數設為1。壁面邊界條件為無滑移壁面,近壁面為壁面函數法。壓力速度耦合采用SIMPLEC 算法,壓力離散采用PRESTO 方法,其余變量采用二階迎風格式,各項收斂殘差精度設為10-5,當溢流口與底流口流量變化小于5%時,視為計算達到收斂狀態。
連續相控制方程:

動量守恒方程:
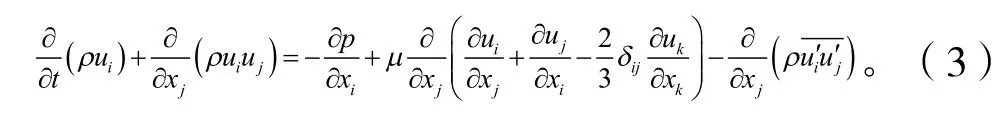
雷諾應力輸運方程:

式中:Dij—湍流擴散項;
Pij—應力產生項;
Gij—浮力產生項;
ij—應力應變再分配項;
?ij—離散相;
Fij—系統旋轉產生項。
2 計算結果與探討
分別采用冪律模式與四參數模式描述鉆井液參與計算。觀察旋流場ZY平面上計算云圖,并繪制ZY平面上Y=45 mm、Y=75 mm、Y=115 mm、Y=150 mm、Y=200 mm 上的數據圖,對比分析兩種模式鉆井液的切向速度場、壓力場及湍流強度差異。
2.1 速度場分析
2.1.1 切向速度對比
全計算域下,冪律模式最大值為20.96 m·s-1,四參數模式為20.47 m·s-1。在ZY平面上,冪律模式最大切向速度為20.49 m·s-1,四參數模式最大為19.95 m·s-1,最大值均出現在中心空氣柱兩旁,如圖4 所示。四參數模式切向速度小于冪律模式,這對二者的固相分離效率影響較大[18]。
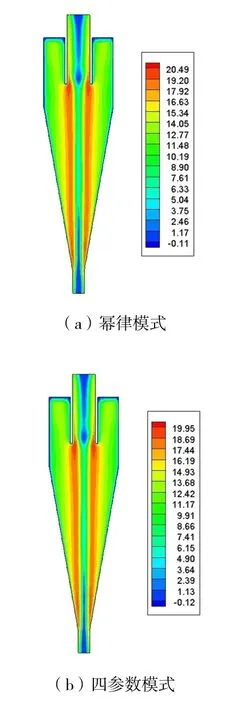
圖4 ZY 平面切向速度圖
兩種模式計算下剪切速度分布相似,均表現為在軸心附近變化劇烈,從Y=45 mm 到Y=200 mm,軸心切向速度變化先由小到大,再由大到小;兩種模式下各個橫截面切向速度極值出現位置相同,極小值出現在Z=0 mm處,極大值出現在Z=±9 mm處。四參數模式各位置切向速度計算結果均低于冪律模式,如圖5 所示。

圖5 Z 軸方向切向速度曲線圖
2.1.2 軸向速度對比
在全計算域中,冪律模式最大軸向速度為 48.38 m·s-1,最小軸向速度為-37.49 m·s-1;四參數模式最大軸向速度為48.85 m·s-1,最小為-35.53 m·s-1,四參數模式的上行流速度明顯低于冪律模式。圖6為冪律模式與四參數模式的ZY截面軸向速度云圖,二者軸向速度最大值出現在靠近底流口位置,最小值出現在溢流口附近,與實際工作情況相符。圖7為兩種模式計算條件下,旋流器內的LZVV 輪廓圖,冪律模式與四參數模式LZVV 形狀相似。在溢流管壁面與旋流器外壁面之間,由LZVV 所包圍的氣包狀區域為循環流區域,四參數模式計算下的循環流區域比冪律模式更大。循環流區域越大,顆粒在此區域停留時間越長[19]。

圖6 ZY 平面軸向速度云圖

圖7 LZVV 輪廓圖
圖8 為Z軸方向軸向速度曲線圖。由于空氣回流的影響,靠近底流口與溢流口處的軸向速度波動明顯,且兩種模式計算值在此位置差異較大。旋流器中間段軸向速度波動較小,兩種模式軸向速度在此差異小。

圖8 Z 軸方向軸向速度曲線圖
2.1.3 徑向速度對比
在全計算域中,冪律模式最大徑向速度為3.45 m·s-1,四參數模式最大徑向速度為3.19 m·s-1。圖9 為兩種模式計算下的ZY平面徑向速度云圖,二者徑向速度最大值均出現在溢流管入口處[20],整體速度分布類似,四參數模式在各個位置徑向速度略低于冪律模式。


圖9 ZY 平面徑向速度云圖
四參數模式與冪律模式徑向速度差異主要出現在溢流管內,其他各個位置的徑向速度相差較小,如圖10 所示。
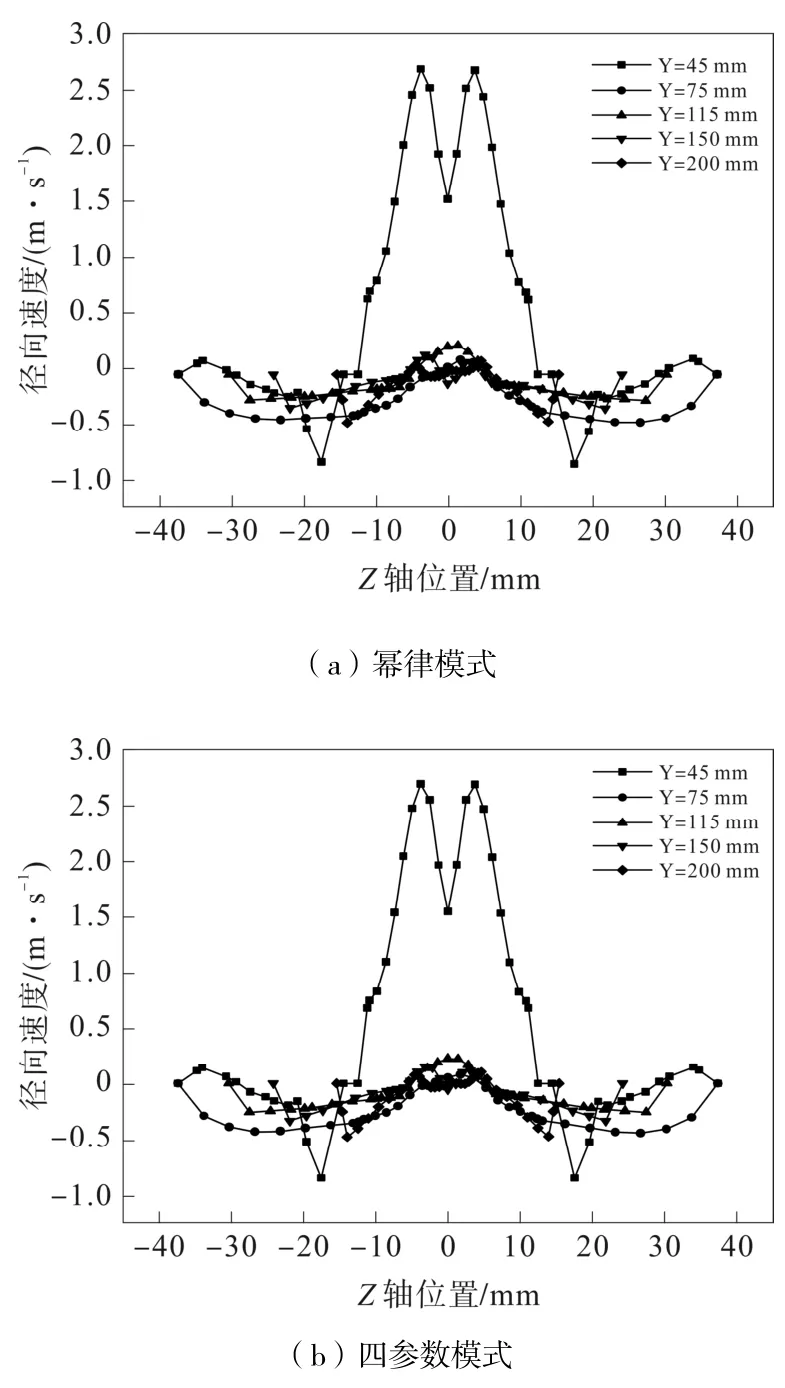
圖10 Z 軸方向徑向速度曲線圖
2.2 壓力分析
2.2.1 靜態壓力對比
在旋流器分離過程中,壓力降是表征旋流器分離性能和能量損耗的主要參數,對分離粒度和分離效率也有重要影響[21]。全計算域中,冪律模式最大靜壓為0.868 MPa,入口與底流口的平均壓降為0.867 MPa。四參數模式下的最大靜壓為0.837 MPa,入口與底流口的平均壓降為0.836 MPa。固相顆粒所受壓力梯度力指向軸心方向,四參數模式內壓力梯度力小于冪律模式。四參數模式入口與底流口平均壓降小于冪律模式,說明四參數模式壓力損耗較冪律模式更小。圖11 為兩種模式下ZX平面靜壓云圖,可以看出最大靜壓均出現在壁面位置,最小靜壓均出現在旋流器中心處。
旋流器Z 軸方向的靜態壓力分布如圖12 所示。
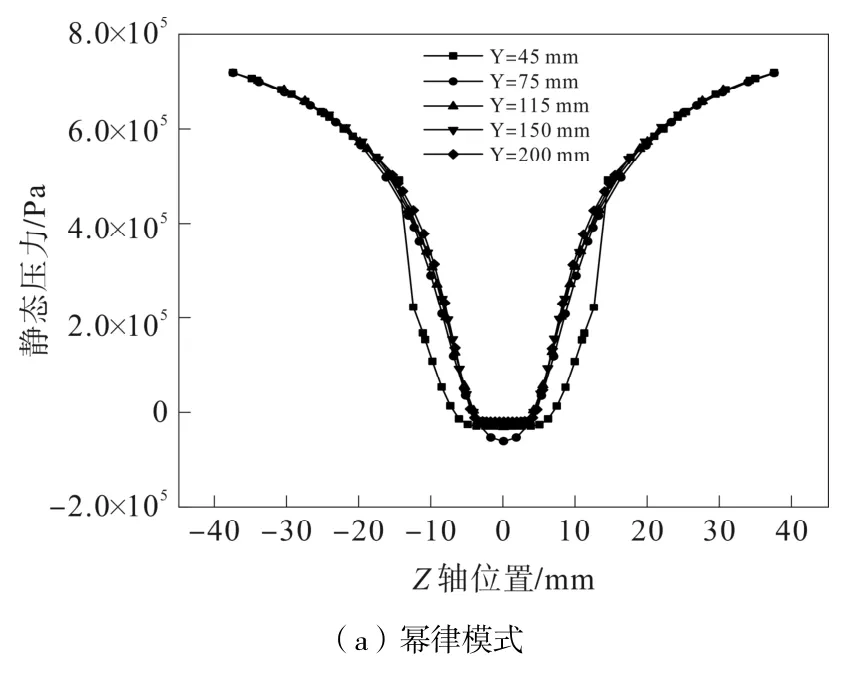

圖12 Z 軸方向靜態壓力曲線圖
兩種模式在軸心附近的壓力分布差異很小,隨著Z的增大,兩種模式的壓力值逐漸增大,在軸心位置出現零靜壓是由于存在空氣柱的原因,符合組合渦流場的壓力分布規律。四參數模壓力增長速率比冪律模式小,在壁面區域時,二者壓力差值達到最大。這說明四參數模式與冪律模式由于本構方程以及流變參數的不同,在旋流器內運動時,對壁面區域壓力的影響最大。
2.2.2 動態壓力對比
在全計算域中,冪律模式計算下最大動態壓力為0.466 MPa,四參數模式計算下最大動態壓力為0.444 MPa。圖13 為ZY平面動態壓力分布云圖,最大值均出現在溢流管壁面,最小值出現在軸心。四參數模式計算值在各個位置均低于冪律模式,溢流管壁面表現最明顯,如圖14 所示。
2.3 湍流強度對比
觀察湍流強度發現,兩種模式計算結果均顯示在溢流口與底流口附近湍流強度最激烈。冪律模式計算下最大湍流強度為7.99,四參數模式最大為7.90,圖15 為ZY平面湍流強度云圖。


圖13 ZY 平面動態壓力云圖

圖14 Z 軸方向動態壓力曲線圖
四參數模式計算下各個位置湍流強度均低于冪律模式,其中在溢流管內表現最明顯,如圖16 所示。
3 結 論
通過四參數模式與冪律模式鉆井液在水力旋流器內速度場、壓力場及湍流強度的對比分析,得出以下結論:
1)四參數模式計算下的切向速度低于冪律模式,這使得在四參數模式中,對固相顆粒的分離效率更低。四參數模式軸向速度整體大小低于冪律模式,上行流速度明顯低于冪律模式;LZVV 形狀相似,四參數模式計算下的循環流區域比冪律模式大,固相顆粒在此模式中停留時間更長。徑向速度差異主要出現在溢流管內。
2)四參數模式鉆井液的靜態壓力低于冪律模式,旋流器入口與底流口的平均壓降低于冪律模式,說明四參數壓力損耗更低;四參數模式中,顆粒所受壓力梯度力將小于冪律模式。四參數模式計算下的動態壓力略低于冪律模式,在溢流管壁面表現最明顯。
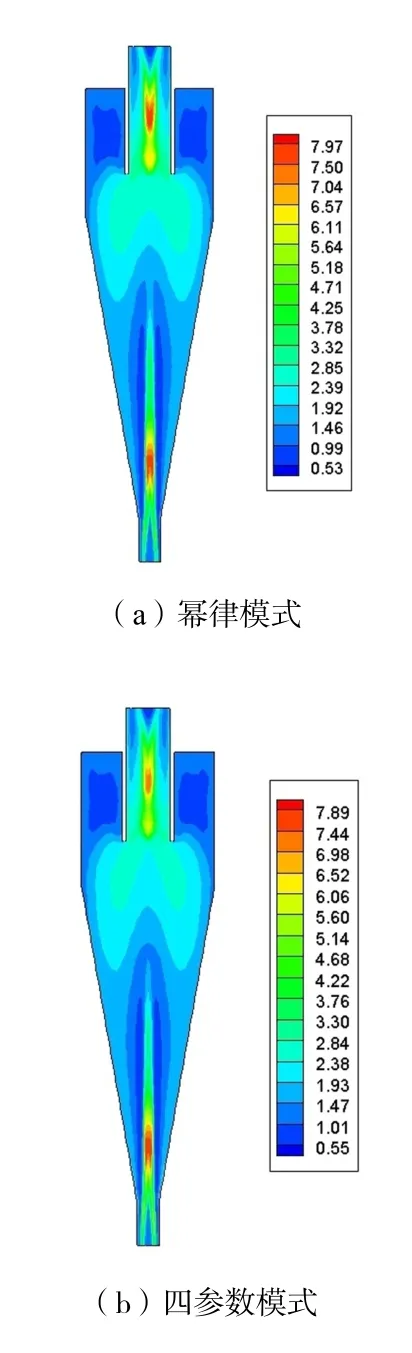
圖15 ZY 平面湍流強度云圖

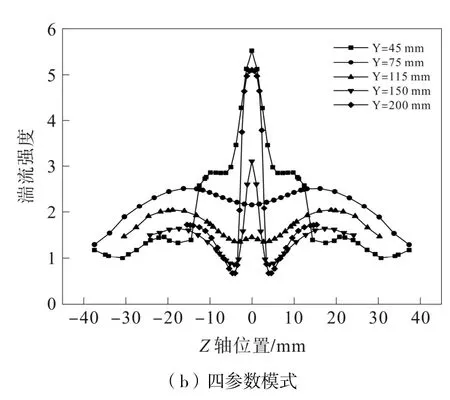
圖16 Z 軸方向湍流強度曲線圖
3)通過對湍流強度的分析,四參數模式計算下湍流強度略低于冪律模式,在溢流管內差異最大。
4)通過四參數模式分析鉆井液的流動行為結果可靠性高于冪律模式。

