基于核密度估計的集成剪枝和增量學習時間序列預測方法*

朱鋼樑

（南京航空航天大學計算機科學與技術學院 南京 210016）

1 引言

時間序列預測（TSP）是機器學習和數據工程領域中一個重要且活躍的研究課題，在許多數據挖掘應用中具有不可或缺的重要性。一般而言，時間序列涉及各種研究領域，例如：經濟（股票價格，失業率和工業生產），流行病學（傳染病病例率），醫學（心電圖和腦電圖）和氣象學（溫度，風速和降雨量）［1］。許多研究關心的是平穩時間序列預測而不是非平穩時間序列預測。然而，實際的時間序列幾乎都是非平穩的，限制了平穩時間序列技術在實際生產生活中的應用。因此，對非平穩時間序列預測的研究變得重要和有價值［2～4］。

在過去的幾十年，神經網絡（NN）憑借其非參數，數據驅動和任何線性和非線性函數的通用逼近的理論特性，引起了時間序列領域的研究人員的極大關注［5］。隨著大量研究人員證明了基于神經網絡的預測系統的優越性［6］，越來越多的研究已經開始在神經網絡的基礎上設計時間序列預測模型［6～11］。然而，對前饋神經網絡（FNNs）參數的訓練將耗費大量時間并導致不同參數層之間的依賴性。基于梯度下降的方法［12］作為迭代訓練參數的常用方法，通常非常耗時，并且當應用于大多數前饋神經網路時，容易使網絡陷入局部最小值。近幾年，黃廣斌等提出了一種新的FNNs學習框架，稱為極限學習機（ELM）［13］。ELM是在單隱藏層前饋神經網絡（SLFNs）的基礎上專門開發的。在ELM中，連接輸入層和隱藏層的權重以及隱藏層的偏差值在學習之前隨機生成，并且在學習過程中保持固定。同時，連接隱藏層和輸出層的權重通過分析計算得到。與傳統的FNNs相比，ELM具有一些重要且有意義的特征［14］：1）效率高，即ELM的學習速度極快；2）穩健性，即，在大多數情況下，ELM具有比基于梯度下降的學習（例如反向傳播（BP））更好的泛化性能；3）最優性，即傳統的基于梯度下降的學習算法可能面臨陷入局部最優，不正確的學習率和過度擬合等問題，ELM將直接得到最優解而不會遇到這些問題。

本文的主要貢獻在于將核密度估計應用于集成系統的動態剪枝和增量學習，提出了一種新的混合時間序列預測算法，稱之為DEPK&ILK。算法融合了動態集成剪枝（DEP），增量學習（IL）和核密度估計（KDE）。DEPK&ILK算法分為三個子過程：1）集成系統生成（Overproduction）；2）動態集成剪枝（DEP）；3）增量學習（IL）。第一個子過程用于生成集成系統的基學習器池。本算法中，基學習器為核方 法 的 在 線 序 列 極 限 學 習 機（OS-ELMK）［15］。OS-ELMK是在ELM的基礎上不斷改進發展而來的。ELMK［16］在ELM的基礎上加入核方法，使ELM具有更好的學習性能。OS-ELMK則是ELMK的在線學習形式。將OS-ELMK作為基學習器，可以隨著新數據的到來不斷更新原有的參數，這一特性在時間序列預測問題上具有重要意義：時間序列的樣本隨著時間順序先后進入模型，并且時間序列的輸出值服從的概率分布往往隨著時間的變化而變化，模型需要不斷的更新才能適應新數據的預測，在第三部分的增量學習中，將會用到OS-ELMK的在線學習特性。算法的第二個子過程為動態集成剪枝（DEP），稱之為DEPK。在此過程中，算法將利用核密度估計（KDE）［17］來進行集成系統的動態剪枝。核密度估計在統計學中是一種非參數估計，用來對未知分布進行估計。對于每一個待預測的樣本，所有的基學習器對此樣本進行預測得到一個預測輸出向量，然后利用核密度估計得到集成系統對此樣本的預測輸出概率密度圖。接著對每一個基學習器，若該學習器對樣本的預測值在概率密度圖上對應的概率越大，則該學習器越有機會用來預測樣本的輸出，最終得到剪枝后的集成系統，最后利用該集成系統對樣本進行預測。算法的第三個子過程為增量學習（IL），稱之為ILK。對于一個待預測的樣本，算法要衡量該樣本是否需要進行增量學習。首先算法定義了一個動態選擇集（XDSEL），XDSEL用來得到待預測樣本的Kp個最近鄰樣本，寫為XRECO（The Region of Competence）。然后對每一個在XRECO中的樣本，集成系統都能產生一個預測輸出向量。同樣的，用該向量可以得到該樣本對應的核密度估計。若該樣本的真實值在核密度估計上位于小概率區間（用一個隨機閾值F衡量），表明集成系統沒有足夠的能力來預測該樣本，則將它并入集合XINCL（該集合用來最終更新集成系統）中。得到最終的集合XINCL后，用該集合去更新集成系統，即對于每一個基學習器，都將XINCL并入它們的采樣集中并更新參數。

2 基于KDE的動態集成和增量學習算法DEPK&ILK

2.1 核密度估計（KDE）

核密度估計用于估計未知的概率密度函數，屬于Rosenblatt和Emanuel Parzen提出的非參數測試方法之一［17］。對于一組數據{ }x1，x2，…，xn，核密度估計通過以下公式得到。

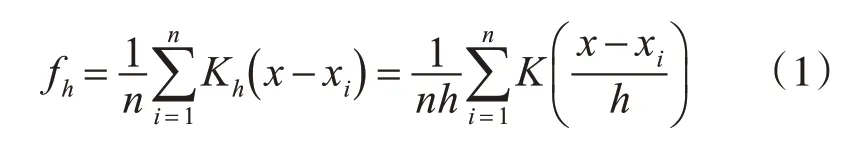
其中，h＞0是平滑參數，稱為帶寬。Kh(x)=為縮放函數。為核函數（非負、積分為1，符合概率密度性質，并且均值為0）。核函數有多種形式。由于高斯內核方便的數學性質，本算法中，令K(x)=φ(x)，φ(x)為標準正態概率密度函數。

2.2 基于KDE的動態集成剪枝算法DEPK

對于一個待預測樣本(x，t)，首先得到一個預測輸出向量：

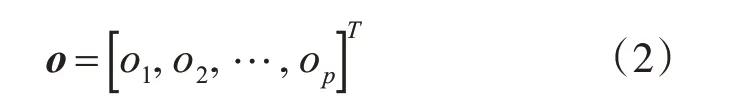
p為集成系統中基學習器的數量。該向量o表示集成系統對待預測樣本的預測輸出向量。得到預測輸出向量后，計算預測輸出的核密度估計。

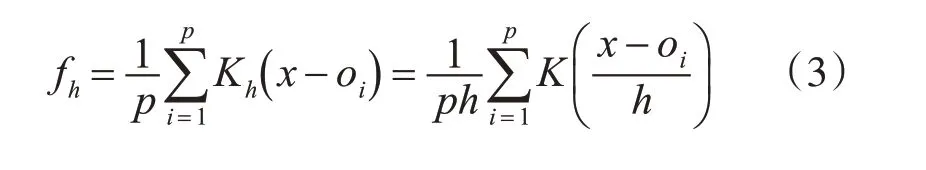
動態集成剪枝算法DEPK的算法步驟如下：

1）令fh，max=max(fh)；

2）對每一個基學習器li，i=1，2，…，p

（1）在區間[0，fh，max]上隨機產生一個值r；

（2）若r≤fh(oi)，則將li并入剪枝集L′。

3）用得到的剪枝集L′去預測樣本的輸出值。

2.3 基于KDE的增量學習算法ILK

本算法中，首先我們定義動態選擇集XDSEL，此集合用來產生Kp個待預測樣本(x，t)的最近鄰樣本集合XRECO（利用K-NN算法得到），用XRECO集合來近似的代表(x，t)，并利用XRECO去實施增量學習算法。基于KDE的增量學習算法ILK的算法步驟如下。

1）隨機產生一個閾值F；

2）對每一個屬于XRECO的樣本(xk，tk)，k=1，2，…，Kp

（1）計算該樣本在集成系統上的KDEfh，k；

3）所有的基學習器都用集合XINCL去更新參數。

3 實驗和分析

3.1 實驗設置

為驗證提出的算法的性能，用三個數據集：1）國際航空旅客數（IAP）；2）IBM股票閉市價格（ICS）；3）每月閉市時道瓊斯工業指數（MCD）作為時間序列實驗數據集。

在利用數據集進行預測之前，首先算法將數據集進行歸一化。歸一化過程可以用下面的方程表示：

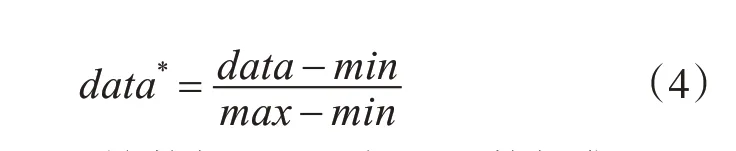
其中data表示原始數據，min表示原數據集上的最小值，max表示原數據集上的最大值，d at a*表示歸一化后的數據。歸一化過程將所有的數據歸一化到[0 ，1]之間。

時間序列預測需要定義時間窗大小，本算法中我們定義時間窗大小為20。定義了時間窗大小后，就可以產生時間序列的數據集。本算法定義最后10%的數據為測試集，用來衡量最終算法的性能。隨機取50%的樣本為訓練集，用來產生基學習器的采樣集。再隨機取20%的樣本作為驗證集，用來訓練參數。取剩下的20%的樣本為動態選擇集XDSEL，產生樣本的k近鄰集合。

對算法的性能評價，我們選擇均方根誤差（RMSE）和平均絕對誤差（MAE）來衡量。

3.2 國際航空旅客數（IAP）

國際航空旅客數（IAP）數據集按月記錄了從1949年1月～1960年12月，國際航空旅客數，具有144個數據點。圖1為該數據集的折線圖。可以看到該數據集表現出強烈的規律性。整體上呈現上升趨勢，同時又有周期性的升降。表1和表2為提出的算法與當前流行的幾種算法比較的實驗結果，由于其余算法不需要用到動態選擇集，因此它們的訓練集占了樣本總量的70%。從結果可以看出，提出的算法無論是RMSE還是MAE，都取得了良好的實驗結果。

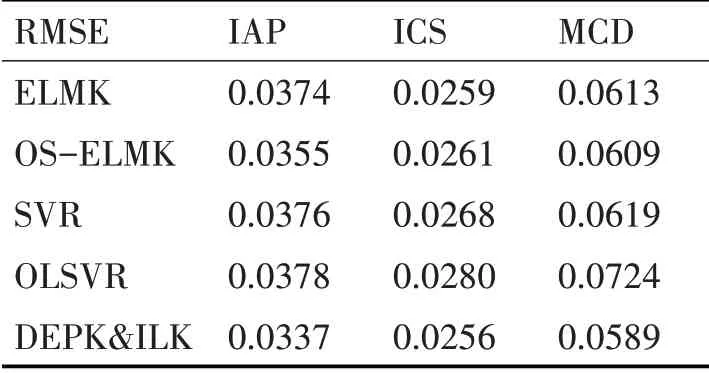
表1 各算法在三個數據集上的RMSE表現

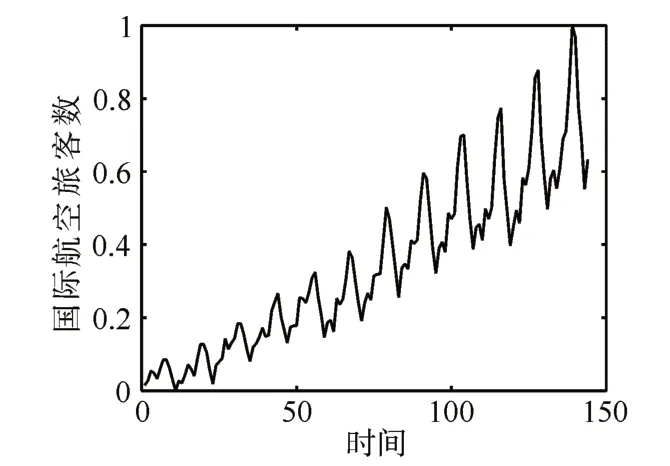
圖1 國際航空旅客數折線圖

3.3 IBM股票閉市價格（ICS）

該數據集記錄了從1961年5月17日到1962年11月2日每天IBM股票閉市價格，具有369個數據點。圖2為該數據集的折線圖。宏觀上看，該數據集并沒有表現出強烈的規律性，原因是股票價格與多種因素有關。從表中結果看出，所有的算法在性能表現上差距不大。尤其是ELMK，OS-SVR和提出的算法性能接近，說明提出的算法不能在所有的數據集上都有優異的表現，這也符合機器學習中“沒有免費午餐”定理。

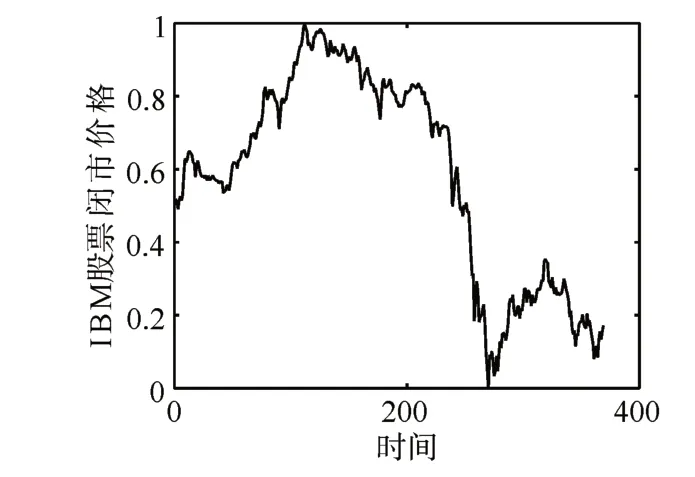
圖2 IBM股票閉市價格折線圖

3.4 每月閉市時道瓊斯工業指數（MCD）

該數據集按月記錄了從1968年8月到1992年10月閉市時的道瓊斯工業指數，具有291個數據點。圖3為該數據集的折線圖。從圖中看出，此數據集上下波動劇烈，兩個波峰之間存在一個周期，但周期性并不明顯。從表1和表2的實驗結果看出，提出的算法獲得了優異的表現，在此數據集上有較低的RMSE和MAE。

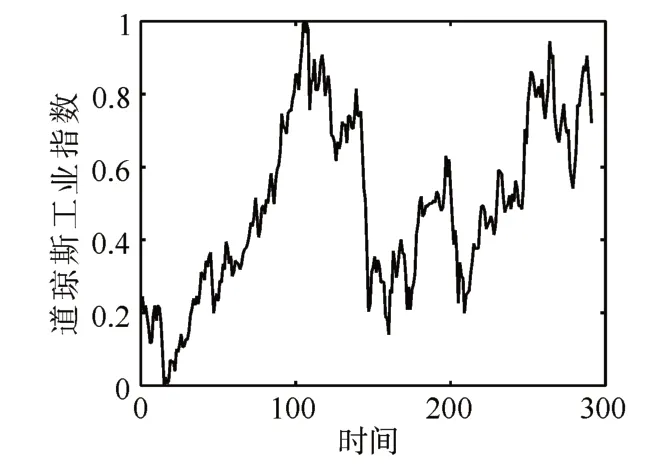
圖3 每月閉市時道瓊斯工業指數折線圖

4 結語

本文提出了一種基于核密度估計的動態集成剪枝和增量學習算法DEPK&ILK。通過在三個數據集上與其他算法的對比實驗，提出的算法具有不錯的預測效果。提出的算法在數據集有較明顯的規律性時對比其他算法有很大的性能提升。但在處理規律性不明顯的數據集時，與其他算法在性能表現上無法拉開較大差距，如何在規律性不強的數據集上也獲得良好的性能是下一步的研究重點。