基于組合賦權的水利工程基礎設施PPP項目風險綜合評價

孫維民

（山東省水利工程局有限公司,山東 濟南 250000）

0 引言

基礎設施PPP項目具有建設周期長、投資大以及資金回籠慢等特點,也決定了在項目建設過程中面臨著諸多的風險。在風險評價方面,陳斌、王蕾等人構建了PPP項目風險指標體系,并建立AHP—熵值法評價模型,對識別出的風險指標進行賦權,根據權重數值大小確定各風險因素對PPP項目的影響程度。石振武、宋瑩琪等人提出德菲爾調研法、網絡分析法、模糊綜合評價法相結合的Delphi—FANP風險評價模型。王帥、郝生躍等運用粗糙集理論對風險因素進行約簡,利用熵值法與G1 法綜合集權的方式進行權重賦值,為構建海綿城市PPP項目風險評價提高新的方式。鑒于風險評價工作比較看重行業專家的實踐經驗,本文提出AHP（層次分析法）—CPA（變異系數法）主客觀相結合的組合賦權法對基礎設施PPP項目風險指標進行評價。

1 基礎設施PPP項目風險指標體系的建立

結合基礎設施PPP項目特點,根據項目生命周期特點劃分為決策階段、準備階段、實施階段及運營階段四個階段,對每階段的風險因素進行識別,再將風險因素劃分為經濟、建設、法律、政治、運營與市場收益六個層面,形成六個一級指標、25 個二級指標的基礎設施PPP項目風險指標體系,見表1。

表1 基礎設施PPP項目風險指標體系

2 模型的構建

2.1 層次分析法

層次分析法（AHP）是一種評價者通過分析復雜系統所包含的因素以及相互關系,將問題或者對象系統分解為多個層次并注入深入進行分析的方法。

第一步：構造兩兩判斷矩陣。層次結構反應因素之間的關系,判斷矩陣表示針對上一層元素而言評價層各元素的相對重要性。

第三步：對矩陣進行一致性檢驗。

1）計算一致性指標CI：

2）計算一致性比例CR：

當CR＜0.10時,判斷矩陣的一致性是可以接受的,否則需要對判斷矩陣進行調整,直到滿足條件為止。

第四步：計算二級指標對總目標的合成權重。求出二級指標相對總目標層的權重向量為W0=（W10,W20,…WN0）T,則：

式中：Wi1、Wi2分別表示一級指標與二級指標相對總目標層的歸一化權重。

2.2 變異系數法

變異系數法（CPA）是一種根據各個指標在所有被評價對象上觀測值的變異程度大小對其進行賦權的方法。其核心思想是通過指標的變異系數來衡量各評價值的差異程度。

第一步：對評價指標進行無量綱化處理。設Xik表示第i個評價指標中第k個評價對象的權值,m為被評價對象的數量,Yik表示無量綱化處理后第i個評價指標中第k個評價對象的權值。

第二步：計算各指標的變異系數。設變異系數為δi,1≤i≤N,則：

其中,

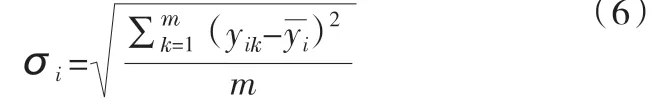
第三步：計算各指標的變異系數權重,并對變異系數進行歸一化處理。

得出二級指標變異系數權重向量為W=（W1,W2,…WN）T。

2.3 組合賦權模型的構建

通過層次分析法得到所有二級指標相對總目標的主觀權值向量：W0=（W10,W20,…WN0）T。通過變異系數法得到所有二級指標相對總目標的客觀權值向量：W=（W1,W2,…WN）T。則組合向量權重為：ζ=（ζ1,ζ2,…ζN）T,其中

α、β表示組合權重中的線性表示系數。其中α≥0, β≥0,α2+β2=1。

假設所有評價指標之間的總離差為Ω,則：

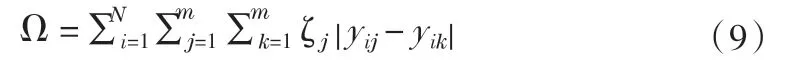
基于離差最大化思想,建立最優模型,如下：

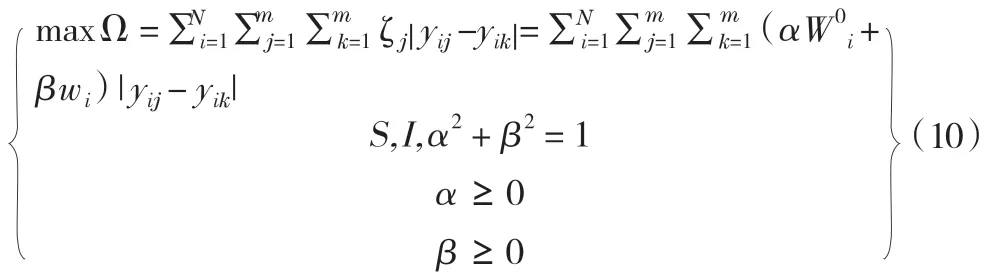
2.4 模型求解

構建Lagrange函數：

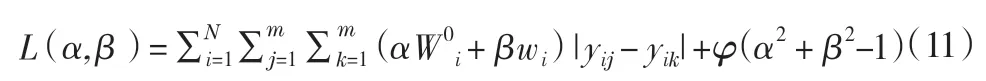
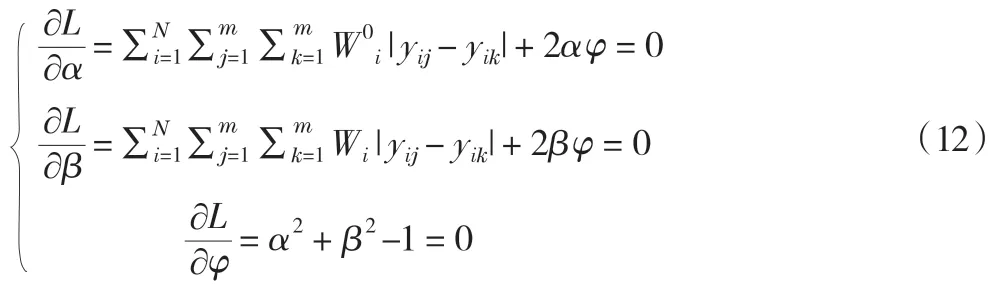
其中, φ為Lagrange乘子,之后對L（α,β ）求導,令：

求解,得出：

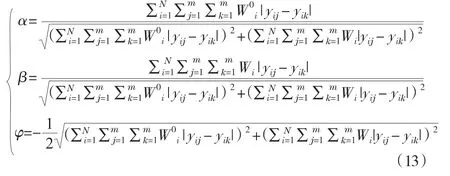
求出α、β后帶入組合權向量：ζ=aW0+ βW,進行歸一化處理,最終得到評價結果。

3 實證分析

某市計劃興修某水利樞紐工程,總工期為三年。本項目計劃采用PPP模式進行建設,社會資本與地方政府部門組成平臺公司（spv）,負責項目的融資、建設以及后期的運營維護工作,特許經營期為20 年。

3.1 主客觀賦權

首先,邀請相關行業專家和一線工作者根據Saaty1-9 級標度法對系統層指標進行兩兩打分并計算權重；其次,采用變異系數法計算客觀賦權權重,本文利用matlab軟件進行計算,結果見表2。

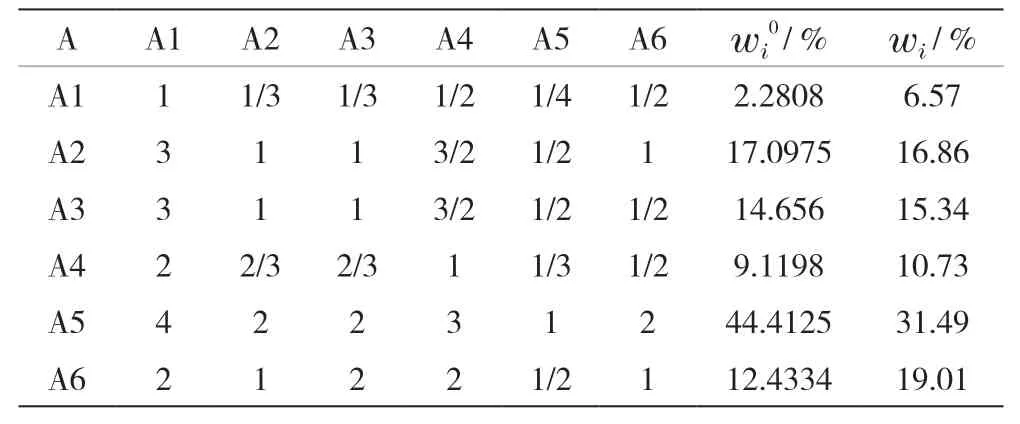
表2 系統層判斷矩陣計算結果

其次,依舊根據行業專家和一線技術人員進行兩兩打分,計算二級指標權重,具體見表3~表8。

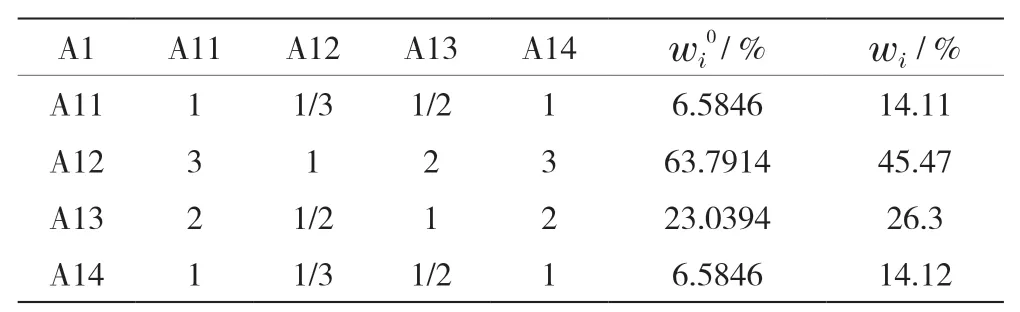
表3 經濟風險指標判斷矩陣計算結果

表4 建設風險指標判斷矩陣計算結果

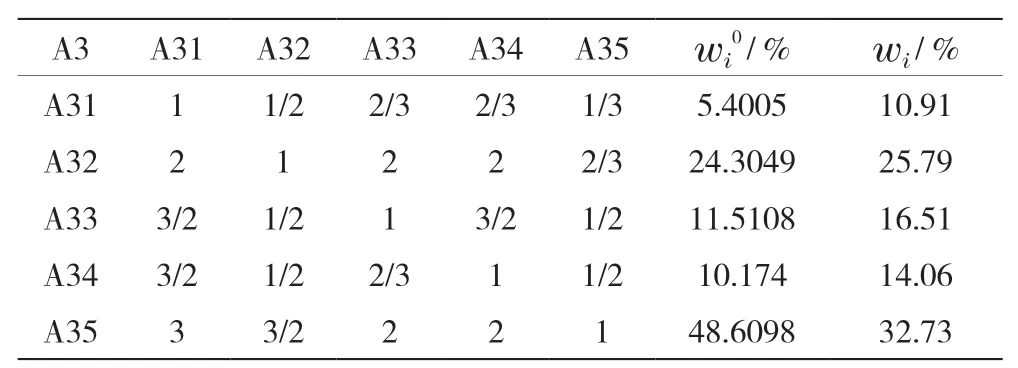
表5 法律風險指標判斷矩陣計算結果

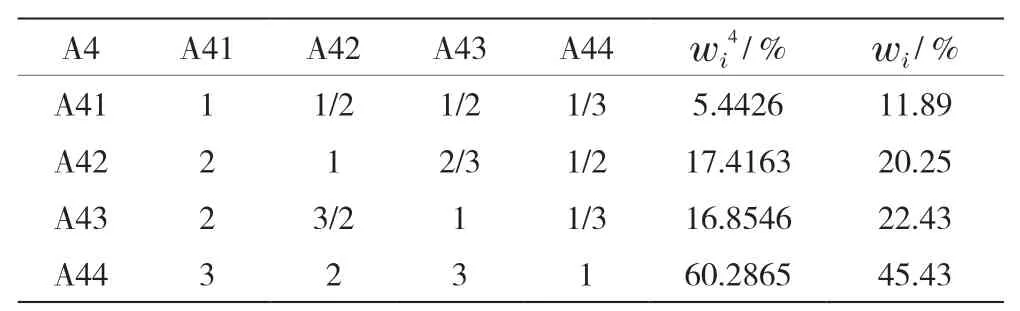
表6 政治風險指標判斷矩陣計算結果

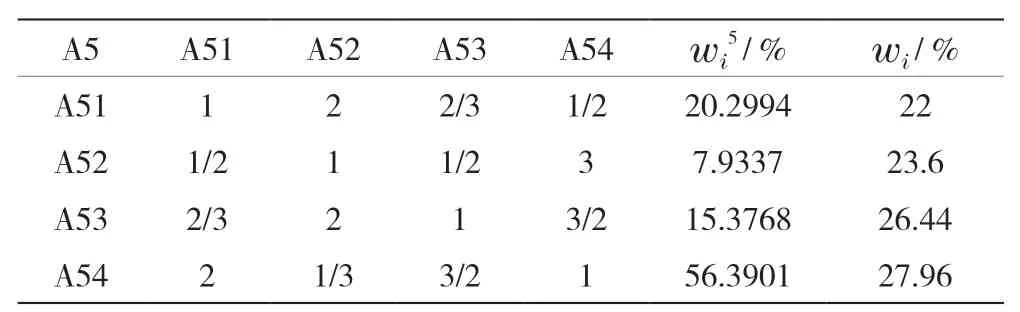
表7 法律風險指標判斷矩陣計算結果

表8 市場收益風險指標判斷矩陣計算結果

3.2 組合賦權

在求得主觀權重與客觀權重之后,將權重數據代入公式（13）,得出α=0.5918,β=0.8061。利用公式求得組合權重,并進行歸一化處理,具體數據見表9。

表9 權重處理結果

層析分析法與變異系數法組合賦值二級指標權重計算結果為：ζ=（0.8362,3.2692,1.7309,0.8362,1.6935,3.1543,8.0477,2.3739,4.5592,3.7909,1.7971,5.2719,3.1494,2.6012,8.2662,1.3343,2.7749,2.9282,7.5164,10.9494,12.1009,11.1945,20.5795,7.52 88,15.0597）。

將二級指標綜合權重進行歸一化處理,得出最終二級指標綜合權重：ζ=（1.0802,7.2231,2.2011,1.0802,2.1876,4.0746,10.3958,3.0665,6.1504,4.897,2.3215,6.8101,4.0683,3.3602,10.6781,1.7233,3.5845,3.7826,9.7095,14.4608,26.5841,9.7255,19.4538）。

系統層指標綜合權重：ζ=（4.7346,16.8905,14.9883,10.4196,36.8081,16.1589）。

系統層指標綜合排名為：A5＞A2＞A6＞A3＞A4＞A1,即就風險指標評分而言,運營風險＞建設風險＞市場收益風險＞法律風險＞政治風險＞經濟風險。因此在項目生命周期中,要積極制定運營階段和建設階段的風險應對策略。在指標層中,建設成本超支風險、法律變更風險、運營成本超支風險、殘值風險、環境污染風險、不可抗力風險與市場競爭風險的綜合評價得分均高于10,表明風險發生的可能性較高,應提前制定針對性的應對方案,達到避免或者減輕風險帶來的損失。

4 結論

運用AHP-CPA組合的賦權方法對水利工程PPP項目風險進行綜合評價,克服了層次分析法主觀性太強的問題,同時,也解決了忽視專家經驗的缺陷,使得主客觀權重更合理。從建立的PPP項目風險評價模型來看,評價過程清晰,計算相對簡單,實現了對工程PPP項目風險因素的定量評價。由此可見,這種風險評價方法不僅克服了單一評價方法的不足,也使得整個風險評價過程更具有可操作性,評價的結果更科學合理,有利于PPP項目的建設發展。