基于改進高斯隨機測量矩陣的切削力信號壓縮感知方法

吳鳳和 張 寧 李元祥 張會龍 郭保蘇

1.燕山大學機械工程學院，秦皇島，0660042.河北省重型智能制造裝備技術創新中心，秦皇島，066004

0 引言

信息物理融合、工業互聯網、物聯網等先進技術的部署和實施均需以數據為基礎，而在機械加工領域，切削力是最為穩定和可靠的關鍵信號之一，可為刀具磨損狀態監測[1]、顫振監測與抑制[2]、加工表面質量控制[3]等提供重要信息。板式測力儀是目前最常用的測力設備，但它存在限制工件尺寸、易受切削液腐蝕的問題。為克服上述缺陷，有學者考慮將力感知元件和信號采集傳輸裝置與機床刀具或刀柄高度集成，形成旋轉式測力系統[4-5]，隨同加工過程進行切削力測量，但刀具切削時高速旋轉，難以采用有線方式傳輸信號，通常利用無線通信協議將信號傳輸至上位機端進行處理及可視化。旋轉式測力系統長期在高速、高頻條件下運行，且集成硬件性能有限，依據Nyquist-Shannon采樣定理限定的頻率采集數據可能導致數據冗余問題，甚至受信號傳輸單元帶寬限制，發生數據堵塞現象。

近些年提出的壓縮感知理論(compressed sensing，CS)[6-7]可以較好地解決上述問題。充分開發信號稀疏特征，將信號壓縮與感知過程進行融合，從而突破Nyquist-Shannon采樣定理頻率限制，實現壓縮式采集，結合高效的重構算法，可實現信號的無失真測量，該過程主要包含信號稀疏模型創建、稀疏信號壓縮測量、壓縮信號重構三個步驟。

作為CS框架的關鍵部分，測量矩陣的選擇和設計直接影響信號壓縮及重構效果。常用測量矩陣類型有完全隨機測量矩陣、結構化隨機測量矩陣以及確定性測量矩陣[8]。以高斯矩陣、Bernoulli矩陣為代表的完全隨機測量矩陣在低維或圖像信號的壓縮感知方面應用廣泛[9-10]，具有測量數少而重構精度高的特點，而局限性在于大存儲量和較高的矩陣隨機性；結構化隨機矩陣包括部分正交矩陣、部分Hadamard矩陣[11]等，該類矩陣通過對高維正交矩陣進行降維和歸一化得到，具備良好的重構精度，但其矩陣構造過程對正交矩陣維數較為敏感，因此應用場合有限；確定性測量矩陣包括循環測量矩陣、Toeplitz矩陣[12]等，該類矩陣易于硬件實現，但受限于現有條件，其矩陣構建速度較慢，難以滿足信號傳輸的實時性需求，同時測量值的取值范圍有限從而影響壓縮效果。此外，也有研究設計了針對信道估計[13]、雷達[14]、振動[15]等特定信號的專用測量矩陣，然而，目前鮮有學者針對切削力信號的壓縮測量矩陣展開研究。

本文基于CS理論，首先分析切削力信號稀疏性，采用離散傅里葉變換(discrete Fourier transform, DFT)正交基構建切削力信號在頻域上的稀疏表示模型；然后考慮加工過程對切削力信號傳輸的實時性需求，且考慮不同主軸轉速和刀具齒數下的信號采樣數據量不同，選擇高斯隨機矩陣作為基礎測量矩陣，并提出一種近似正交三角(QR)分解與最小相關系數法相結合的高斯隨機測量矩陣優化方法，進一步提高測量矩陣性能，實現切削力信號壓縮測量；最后利用壓縮采樣匹配追蹤算法對切削力信號進行高效重構，并通過現場采集的切削力信號對其有效性進行驗證。

1 壓縮感知理論

任意一個一維離散信號可以由一組正交基線性表示：

(1)

式中，N為原始信號長度；x為一維離散時間信號，維度為N×1；Ψ為稀疏基，Ψ=[ψ1ψ2…ψN]，維度為N×N，ψi為列向量；α為稀疏向量，維度為N×1，αi為元素。

取一與Ψ不相干的矩陣，將原始信號x映射至低維空間：

(2)

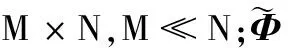
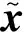
(3)

式(3)的常用求解方法包括以基追蹤(basic pursuit, BP)為代表的最優化逼近方法、以正交匹配追蹤(orthogonal matching pursuit, OMP)[16]為代表的貪婪算法以及以迭代硬閾值(iterative hard thresholding, IHT)為代表的非凸方法。綜合考慮測力系統硬件水平和重構效率需求，本文選擇貪婪算法中的壓縮采樣匹配追蹤(compressive sampling matching pursuit, CoSaMP)[17]算法作為信號重構算法。

2 切削力信號稀疏表示

具有稀疏性的信號表現為僅有少數元素非零。一般情況下自身具備稀疏性的信號較少，但經過某種變換可以挖掘信號的稀疏特征。對于一維信號，通常借助正交變換方法實現信號稀疏表示，如傅里葉變換、正(余)弦變換和小波變換。本文分別利用上述方法進行切削力信號稀疏建模，分析不同正交基下的切削力信號稀疏表示效果，并最終選擇DFT基作為稀疏正交基。

通過切削實驗并采用自主設計的旋轉式測力系統[18]獲取切削力信號，初始采樣頻率為4 kHz，從中選取2 s數據，并以500 Hz頻率對其重新采樣，得到原始切削力信號，如圖1所示。將其絕對值按降序排列后如圖2所示。可以發現，原始切削力信號中的絕大多數元素均為非零元素，因此，切削力信號在時域上是非稀疏的。

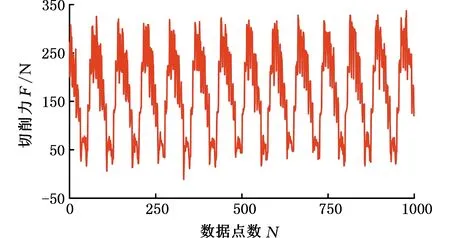
圖1 原始切削力信號

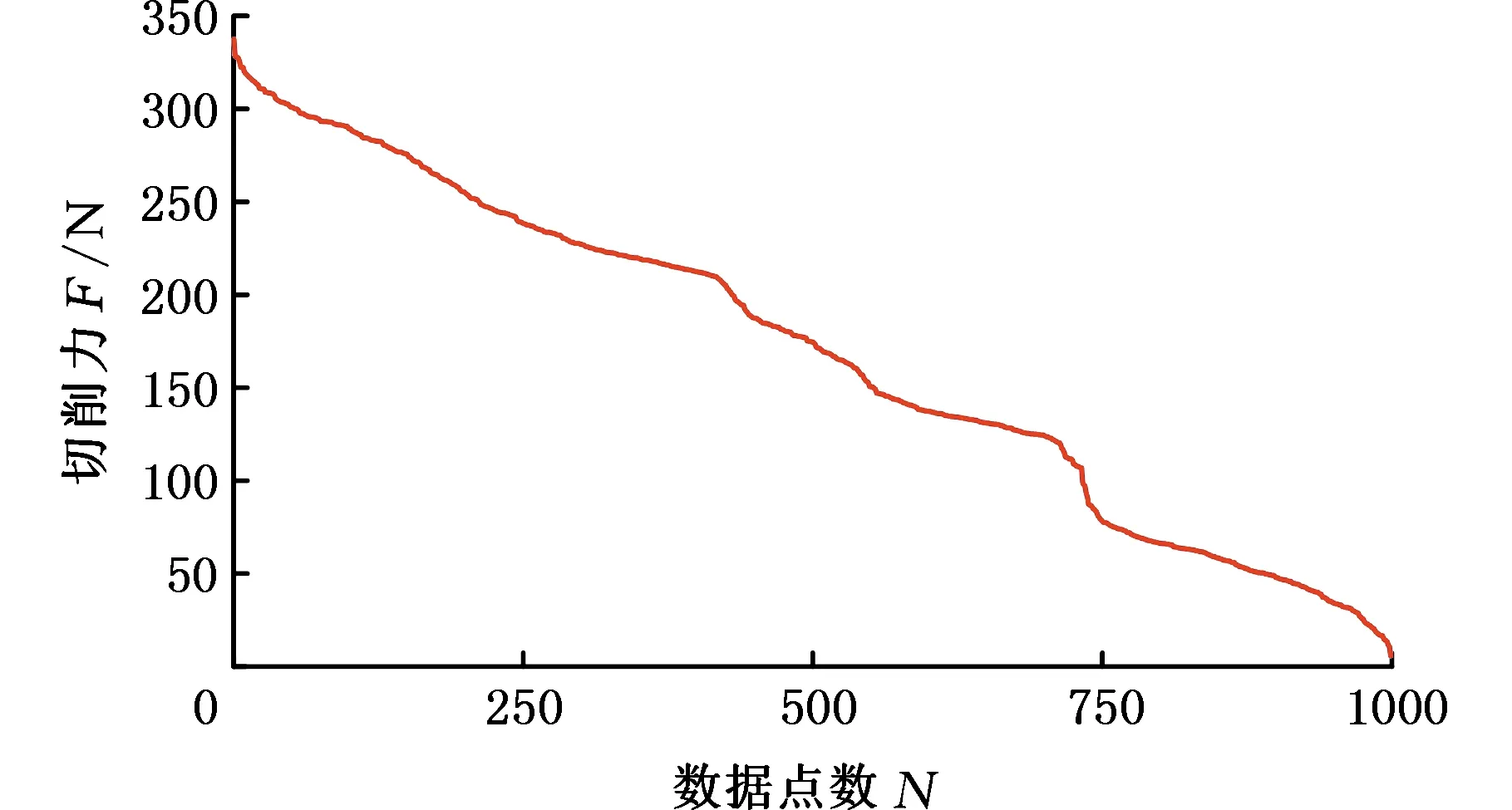
圖2 排序切削力信號

分別利用DFT、離散余弦變換(discrete cosine transform, DCT)和離散小波變換(discrete wavelet transform, DWT)獲取切削力信號的頻域波形，其中DWT基于Haar小波函數，分解等級為10級。對變換系數按絕對值降序排列后如圖3～圖5所示，可以看出三種情況下的變換系數均呈現快速下降趨勢，僅包含少量大系數值。以fmax表示變換系數最大值，在DFT、DCT、DWT三種變換下，變換系數值大于0.01fmax的數量分別為103、105和249。可見，經過DFT處理的切削力數據稀疏性更佳，稀疏度K為103。

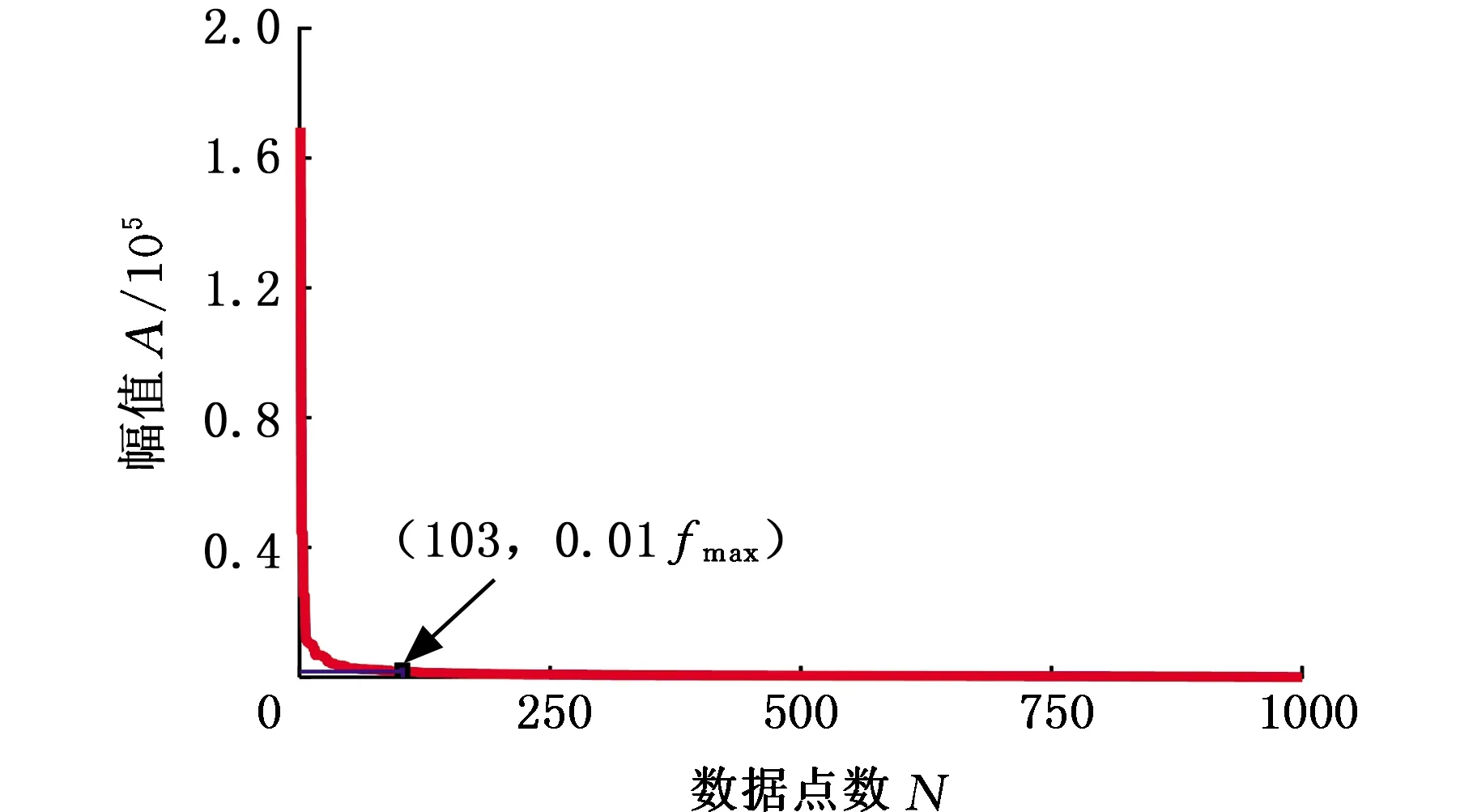
圖3 切削力信號DFT排序

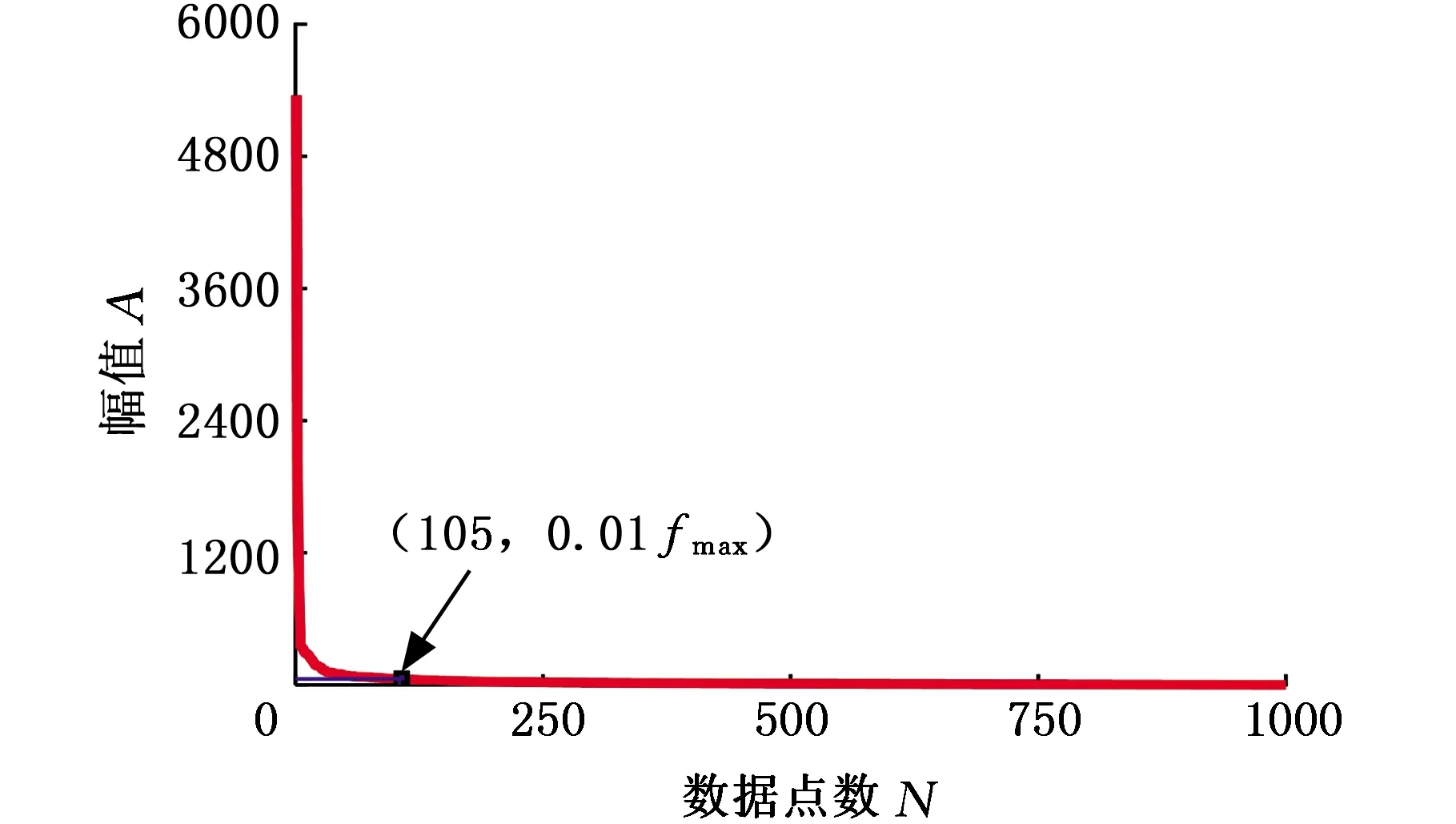
圖4 切削力信號DCT排序

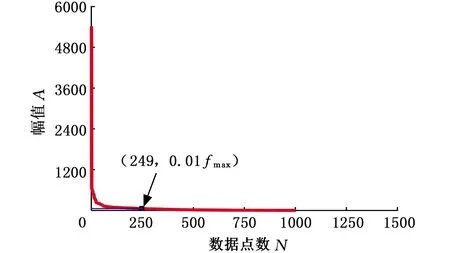
圖5 切削力信號DWT排序

3 改進高斯隨機測量矩陣設計

為實現信號的高精度重構，測量矩陣設計需符合兩項要求：一是測量矩陣與稀疏變換基不相干；二是觀測矩陣應符合約束等距性(restricted isometry property, RIP)。本文以高斯隨機測量矩陣為基礎構建觀測矩陣，為了實現切削力信號的精確重構，其測量值需滿足：

M≥CKln(N/K)

(4)

式中，C為一常數。

對于圖1所示的切削力信號數據，其信號長度N=1000，稀疏度K=103，經計算僅需測量M=235個數據點即可以較高的精度重構出原始切削力信號，壓縮比可達76.5%。

現有理論證明，M滿足式(4)的高斯隨機測量矩陣能以較高的概率符合RIP條件。為進一步提高測量矩陣的信號壓縮性能，使信號重構時的精度更高，本文結合近似QR分解和最小相關系數法對高斯隨機測量矩陣進行改進。

根據矩陣分解理論，矩陣的相干性很大程度上取決于矩陣的最小奇異值，表現為最小奇異值愈大則矩陣的相干性愈弱。因此，從降低測量矩陣與稀疏變換基相干性角度出發，盡可能增大高斯隨機測量矩陣的最小奇異值，可增強矩陣獨立性，從而使矩陣進一步滿足RIP條件。

考慮到QR分解能夠增大矩陣奇異值，首先利用標準QR分解將ΦM × N分解如下：

Φ=(Q·R)T

(5)

式中，Q為方陣，且QH·Q=Ir；R為具有正對角元的上三角陣。

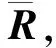
(6)

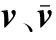
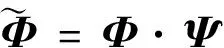
(7)

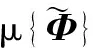
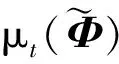
(8)

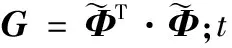
近似QR分解及最小相關系數法相結合的高斯隨機測量矩陣優化方法流程如圖6所示。

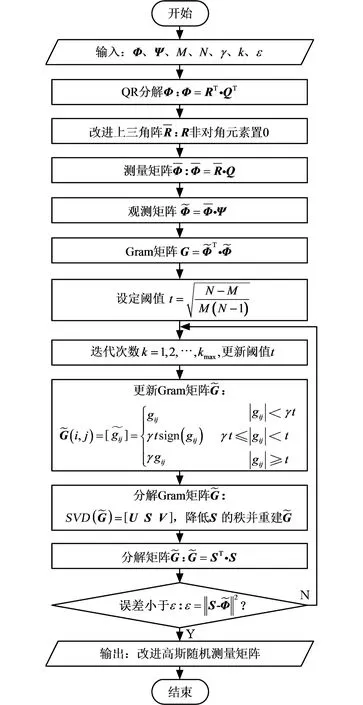
圖6 測量矩陣優化流程圖

4 算法實現步驟

利用本文提出的改進高斯隨機測量矩陣實現切削力信號壓縮感知的步驟如下：

(1)基于實驗獲取的切削力信號，利用DFT正交基對該信號進行稀疏表示，獲取其先驗知識和稀疏度K。

(2)為使測量矩陣進一步滿足RIP條件，結合近似QR分解及最小相關系數法對高斯隨機測量矩陣進行優化。

(3)借助上述改進的測量矩陣，利用y=Φ·x，對原始信號x進行壓縮測量，將其從N維信號映射為M維壓縮信號y。

(4)通過無線傳輸網絡將壓縮信號y傳輸至上位機端，綜合測量值y、測量矩陣Φ和稀疏基Ψ，并通過CoSaMP算法重構獲得稀疏向量α。

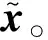
5 實驗及結果分析

為了驗證改進測量矩陣對切削力信號的壓縮性能，針對圖1中的實測切削力信號，分別通過標準高斯隨機測量矩陣和近似QR分解、最小相關系數法以及結合近似QR分解與最小相關系數法優化的高斯隨機測量矩陣進行壓縮測量，計算四類矩陣的相關系數μt，它與對應測量矩陣列向量組合數量T的分布關系如圖7所示。

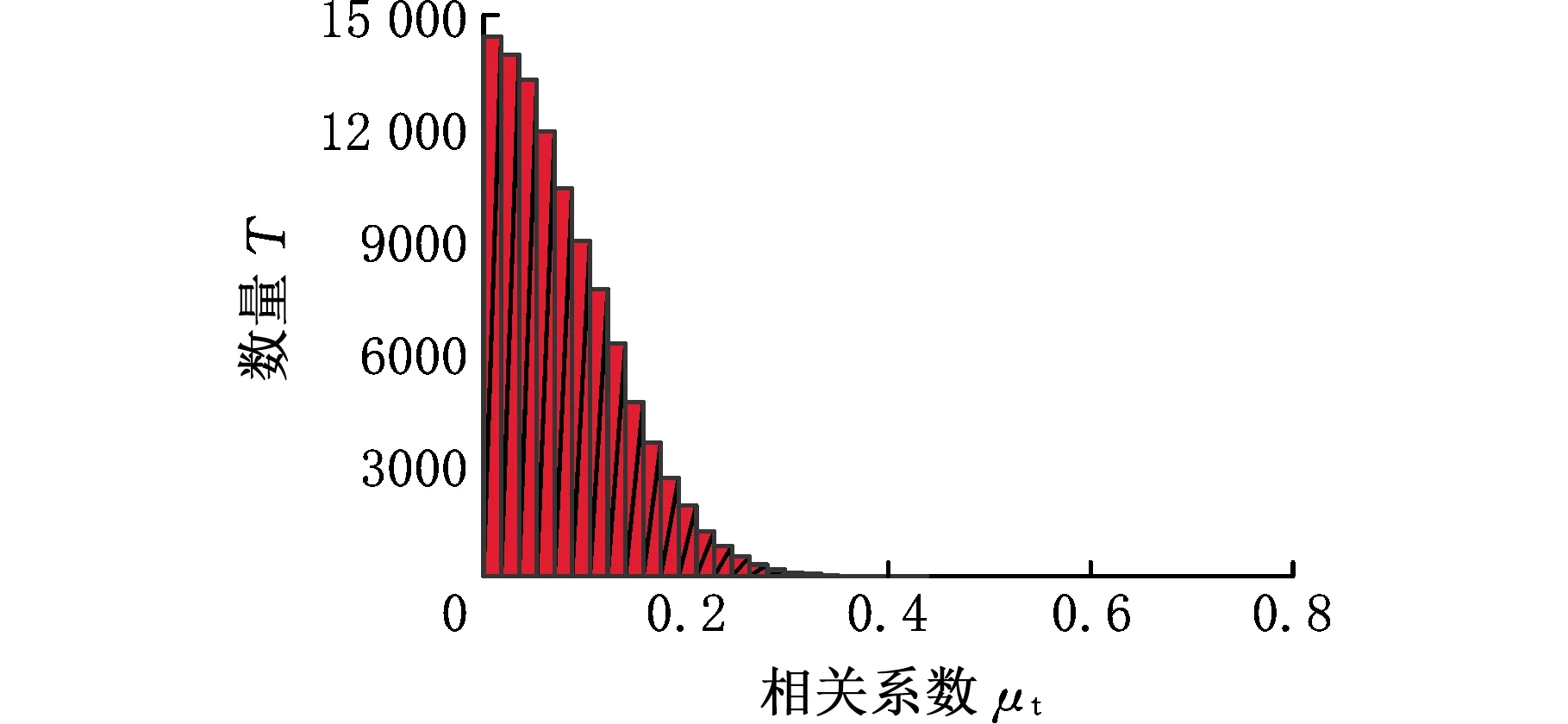
(a)高斯隨機測量矩陣

為了驗證改進測量矩陣的適用性，選擇長度N=100、稀疏度K=10的一段信號作為測試樣本，分別通過四類測量矩陣進行壓縮測量，其相關系數分布如圖8所示。

由圖7、圖8可以看出，在圖1實測切削力信號和測試信號數據下，四類測量矩陣的最大相關系數分別為0.4381、0.4276、0.3830、0.3719和0.6434、0.5083、0.4103、0.3421。因此，本文提出的優化算法在降低測量矩陣相干性方面效果明顯，由該測量矩陣構建的觀測矩陣可進一步滿足RIP條件，從而準確重構原始信號。

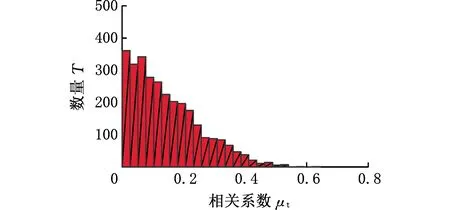
(a)高斯隨機測量矩陣

為進一步測試改進測量矩陣的使用性能，分別利用四類測量矩陣對圖1實測切削力信號和測試信號進行壓縮采集。定義壓縮比

c=(N-M)/N

(9)

設定c為0.5、0.55、0.6、0.65、0.7、0.75、0.8，在四種情況下分別重構1000次，取其重構平均值和均方值誤差，實測切削力信號和測試信號的重構結果分別如表1～表4所示。

由表1～表4可知，隨著信號壓縮程度升高，四類測量矩陣的重構誤差均有所增大，其中，經過本文方法改進的高斯隨機測量矩陣無論在重構平均值誤差還是在重構均方值誤差方面的表現均優于其他三類矩陣，它不但重構精度較高，且在信號恢復時的穩定性更佳。

表1 實測切削力信號平均值誤差

表2 實測切削力信號均方值誤差

表3 測試信號平均值誤差

表4 測試信號均方值誤差

在重構算法選擇方面，當壓縮比c為0.5、0.55、0.6、0.65、0.7、0.75時，采用OMP和CoSaMP兩種算法對圖1所示的切削力信號進行重構，每個壓縮比水平下運行25次，結果取其均值，對比兩種算法在重構時間及重構精度(以信號重構均值偏差為評價指標)方面的差異，結果如圖9所示。

圖9數據表明，伴隨著信號壓縮程度不斷增加，CoSaMP算法的重構效率顯著提高，而重構均值偏差略有增大。在壓縮比c=0.75的情況下(接近測量矩陣限定的最高壓縮比)，CoSaMP算法重構所需時間為0.027 16 s，相比于OMP算法的0.713 12 s，重構效率大大提高；在重構精度方面，CoSaMP算法的重構均值偏差為2.028%，相比于OMP算法的1.125%僅增加1%；考慮到工業現場對力信號的傳輸效率要求較高，而兩種算法的重構準確性差距較小，所以CoSaMP算法同OMP算法相比更加適合實際切削場合的應用。

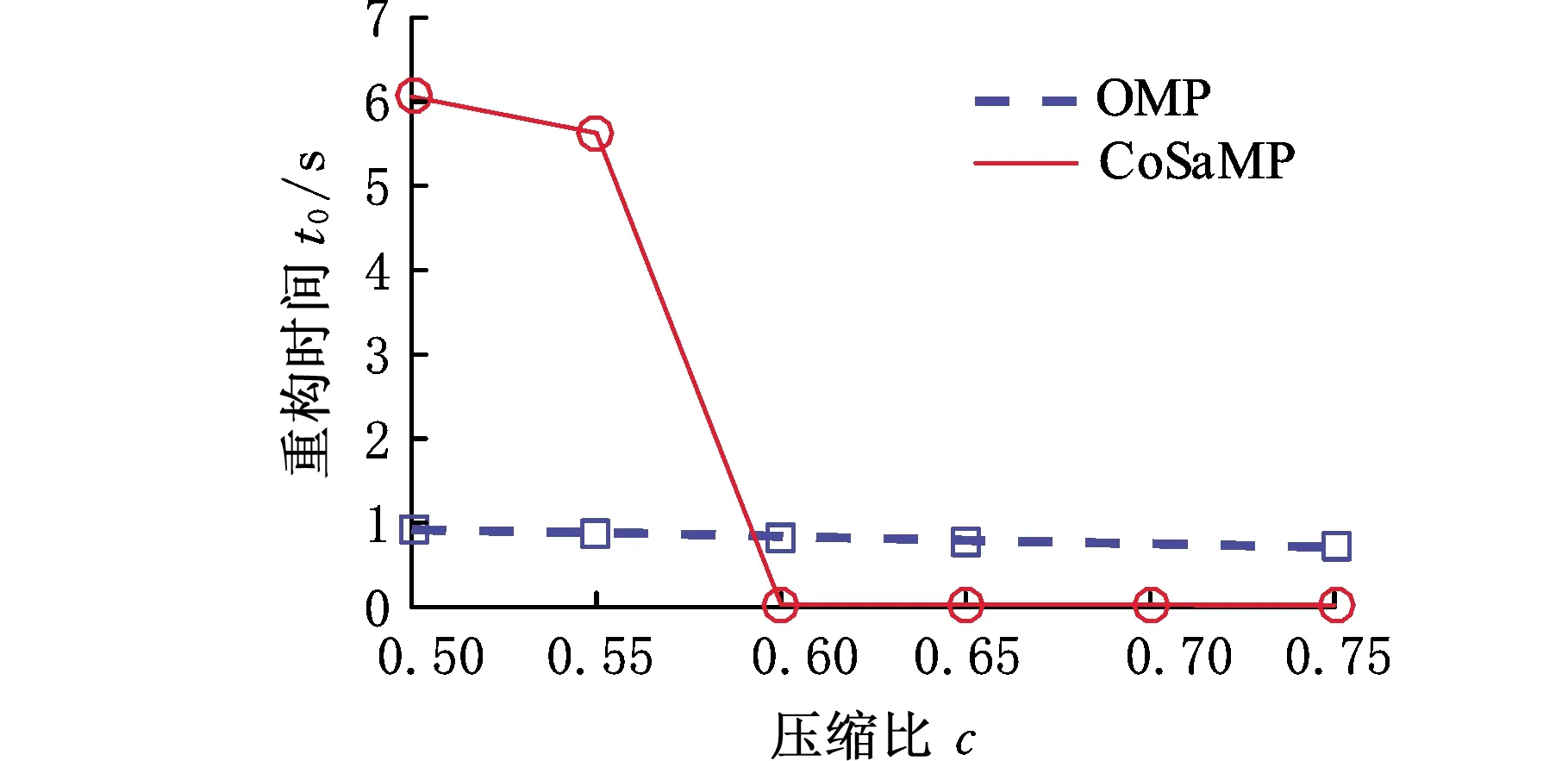
(a)重構時間對比圖

在壓縮比c=0.7的條件下，利用本文提出的切削力信號壓縮感知方法對圖1中的切削力信號進行重構，重構前后信號對比如圖10所示，重構誤差為2.10%，重構時間為0.016 s；另取一段實測鉆削力信號(稀疏度K=201)，在c=0.6的條件下對其進行重構，重構前后信號對比如圖11所示，重構誤差為1.1%，重構時間為0.052s。綜上，本文提出的切削力信號壓縮感知方法能夠滿足切削力信號的傳輸精度和實時性需求。

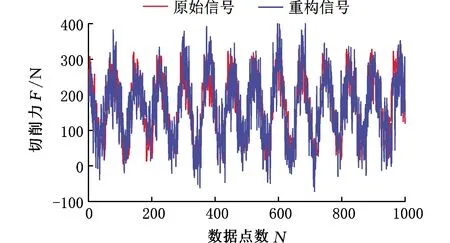
圖10 銑削力信號重構結果對比圖

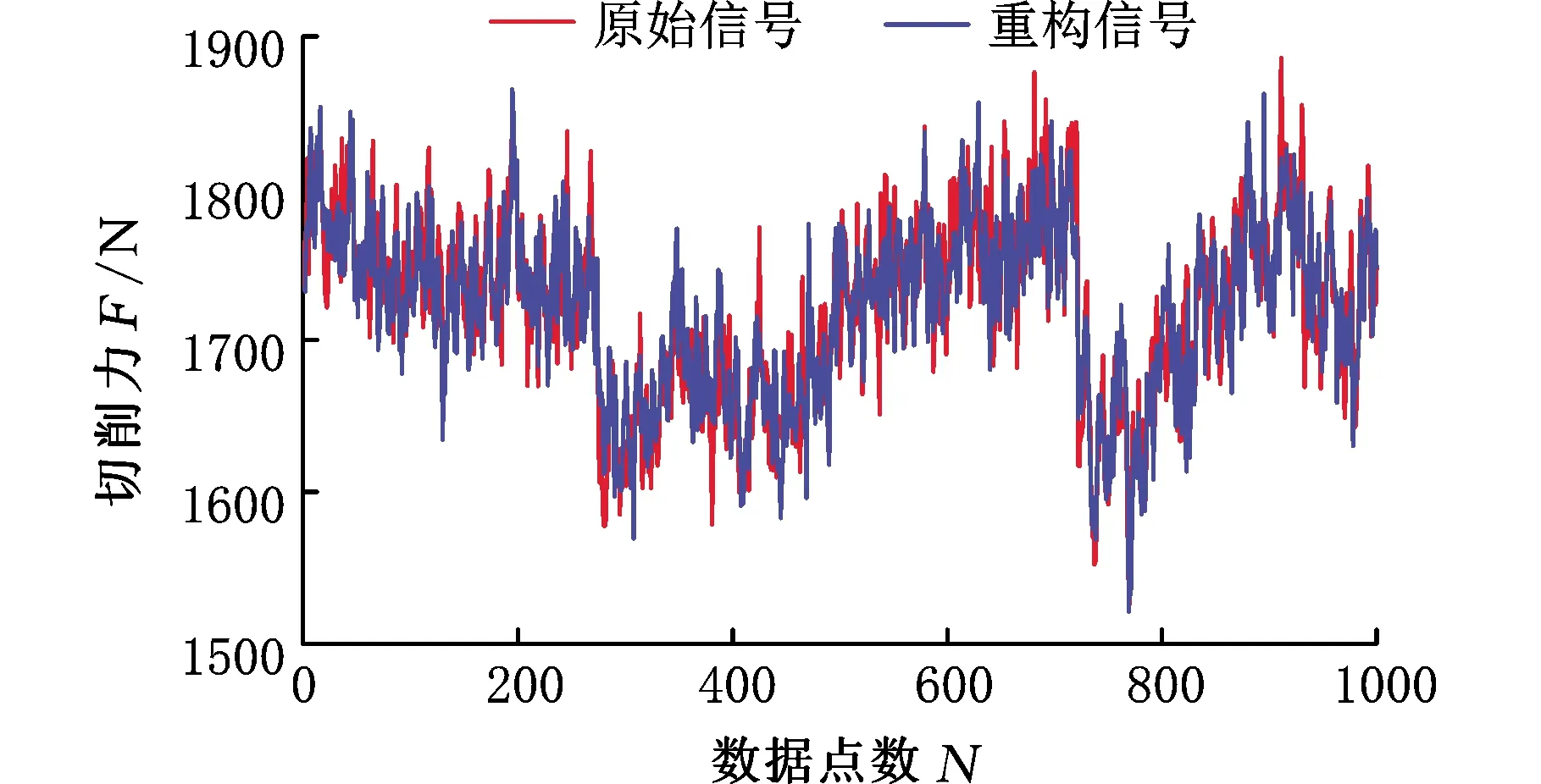
圖11 鉆削力信號重構結果對比圖

6 結論

針對高速切削中依據傳統Nyquist-Shannon采樣定理采集數據易造成信號冗余和數據堵塞問題，本文將壓縮感知理論應用于切削力信號采集過程。針對DFT正交基稀疏表示的切削力信號，選擇高斯隨機矩陣作為基礎測量矩陣，并提出近似QR分解與最小相關系數法相結合的優化方法對高斯隨機矩陣進行重新設計，使其進一步符合RIP條件，并極大地壓縮了數據量，結合高效的CoSaMP算法，實現力信號快速重構。仿真測試結果表明，改進的高斯隨機測量矩陣相較于其他三類矩陣具有更高的重構精度和穩定性，利用本文提出的方法對測力系統采集的切削力信號進行壓縮重構，重構誤差為2.10%，重構時間僅為0.016 s，可滿足工業現場對切削力信號的傳輸精度和實時性需求，此外，本文提出的壓縮感知方法也可為振動、聲發射等信號的高效采集與傳輸提供借鑒。