問題圖式在“輕彈簧”模型問題解決教學中的應用

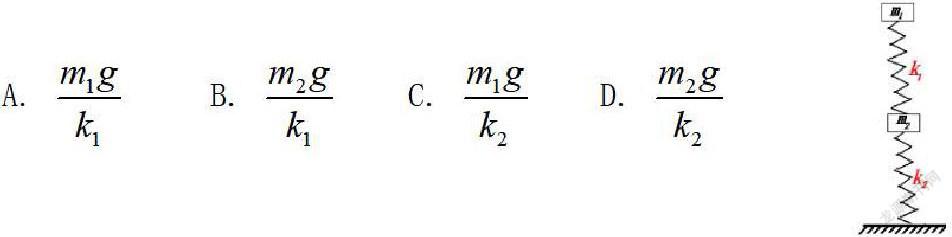
摘要：問題圖式與問題解決是相互影響，問題解決的過程就是篩選合適的問題圖式的過程。本文以“輕彈簧”模型為例，運用問題圖式理論進行教學設計，解決彈簧關聯物的位移一類問題，闡述如何幫助學生建構物理問題圖式。

關鍵詞：問題圖式;問題解決;彈簧模型

一、前言

如今，“核心素養”儼然成為教育界中的熱點。物理學作為一門科學學科的性質在很大程度上取決于它所使用的現實模型，而科學思維包括基于經驗事實建構理想模型的抽象概括過程和分析綜合、推理論證等科學思維方法的內化。在物理教學中，學生較弱的問題解決能力是一個突出的問題。為了克服這一困難，大多數教師試圖選擇“題海戰術”，讓學生通過多做題練習而領悟其中的方法。然而，學生沒有習得一類問題的本質結構特征，缺乏解決這類問題的知識和策略。因此，當學生面對新情境的習題時，無法在認知結構中找到符合其結構特征的圖式來有效解決問題。這對于培養學生分析、解決問題的能力的成效不大。本文以“輕彈簧”模型教學為例，運用問題圖式理論幫助學生提高對該類型的物理問題解決的能力。

二、問題圖式概述

問題圖式，指的是在經歷解決大量本領域常規問題的過程中，專家形成了針對領域中特定類型問題解決的一種整體性表征方式。具體來說，它將解決某類問題所需的陳述性知識和程序性知識包括與問題類型有關的原理、概念、關系、規則和操作程序構成的知識綜合體，與成功解決問題密不可分。物理學科中對問題圖式的研究非常多，齊（M.T.Chi）等人提出，專家和新手的主要區別在：專家的圖式除了有大量的陳述性知識外，還有程序性知識，明確相關問題的結構特征;新手的圖式僅有大量的相關物理問題的陳述性知識，缺乏抽象的解決方法。[2]所以，專家能更加高效地解決問題。總之，問題圖式主要包含三方面內容：問題特征，某一特定類型問題的內在本質結構特征;知識，解決此類問題所必需的專業領域知識;策略，解決此類問題的特定策略，主要是針對該類問題有效的強方法。[3]以力學問題為例，專家在解決一定量的力學問題后，推測專家形成以下的針對力學問題解決的圖式，[4]如表1所示。

問題圖式和問題解決是相互影響的。問題圖式不僅作用于問題表征直至問題的解決，反過來，問題解決也是促進問題圖式的獲得。解決者對問題進行物理表征時總是先從長時記憶中提取與相應問題相似的問題圖式，問題解決的過程基本就是篩選合適的問題圖式的過程。[5]當學生面對一個具體問題情境時，首先對問題進行表征，分析問題的起始狀態和目標狀態，了解問題的要求和約束條件，發現它們之間的聯系，進而建構問題空間，從長時記憶系統中的原有問題圖式或知識結構中提取有關信息，將當前問題和原有問題圖式進行結合。而在問題解決過程中，問題圖式又得以修正、概括化和精細化，進而形成新的問題圖式。[6]

三、“輕彈簧”模型的問題解決教學

（一）教學設計說明

本節課以運用胡克定律求解輕彈簧關聯物的位移問題的問題圖式為教學目標，圍繞問題圖式的習得和應用進行設計，通過提供典型的樣例給學生嘗試練習，引導學生分析總結，構架此類問題的圖式，再通過變式練習，使學生在具體情境中辨別此類問題的本質特征，鞏固此類問題的解決方法。

（二）教學案例分析

【教學內容】彈簧關聯物的位移一類問題的解決

【教學過程】

教學環節一：樣例學習

師：前面學習完彈力和胡克定律，我們發現試題當中涉及到胡克定律都離不開彈簧模型，那今天我們先來解答彈簧關聯物的位移這一類問題。請同學們先嘗試完成下面一道例題。

例1：如圖所示，豎直放置在水平面上的勁度系數為k的輕彈簧上疊放著兩物塊P、Q，它們的質量均為m，均處于靜止狀態。若將物塊P緩慢提起直到與物塊Q分離。求物塊Q上升的位移。

（學生思考，嘗試解答，然后教師分析解決。）

師：完成上一道例題，請同學們完成接下來的一道習題。

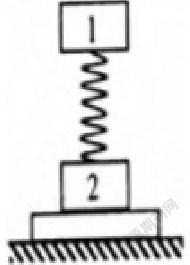
例2：如圖所示，質量分別為M1和M2的1、2兩物體，用勁度系數為k的輕質彈簧相連，處于靜止狀態。現對物1施以豎直向上的恒力F，并將其緩慢提起，當物2對地恰無壓力時撤去F，物體1由靜止向下運動至最大速度時，求物1下落的位移。

（在教師的指導下，學生思考分析并解決。）

教學環節二：彈簧關聯物的位移問題的問題圖式的習得

（1）學習解決此類問題的方法

師：前面我們求解了兩道問題，請同學們思考，解決這兩道題所用的方法有什么特點？

生1：都用了胡克定律進行求解。

生2：先分析物體的初末狀態，利用題干給出的臨界條件（如兩物塊剛好分離、物塊恰好對地無壓力等）進行列式。

生3：如果初末狀態的彈簧都是壓縮或者拉伸的，將兩個狀態的彈簧形變量直接作差;如果彈簧是由拉伸到壓縮或者由壓縮到拉伸的狀態，將兩個狀態的彈簧形變量求和。

師：分析以上兩道題的求解過程，其實就是彈簧的彈力變化量和彈簧的實際形變量的關系。解這類問題時，一般先理清初始狀態和目標狀態的彈簧的彈力變化，注意彈力方向的改變，由胡克定律可得彈簧關聯物的位移Δx=ΔF/k。

（2）分析此類問題的本質結構特征

師：我們分析完這兩道題的方法，那這兩道題在研究對象、運動過程和形式上有什么相同的地方嗎？

生1：都涉及兩個物體和一根彈簧，末狀態至少有一個物體與彈簧關聯。

生2：物體和彈簧關聯的起始位置和問題的終止位置并不是彈簧的原長，往往是已經發生形變的位置。

生3：待求量是彈簧關聯物的位移。

師：以上幾位同學分析得很好，觀察得很仔細，將以上的分析綜合起來就更全面了。

（3）學習并形成解決此類問題的圖式

教師分析概括，并板書：

教學環節三：圖式的運用

師：通過練習前面兩道習題以及老師的分析，請同學們完成下面兩道題。

練習1：如圖所示，兩木塊的質量分別為m1和m2，兩輕質彈簧的勁度系數分別為k1和k2，上面木塊壓在上面的彈簧上（但不拴接），整個系統處于平衡狀態。現緩慢向上提上面的木塊，直到它剛離開上面彈簧。在這過程中下面木塊移動的距離為（ ）

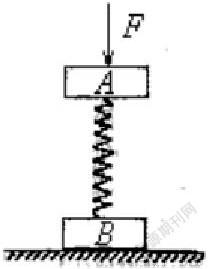
練習2：用勁度系數為k的輕彈簧把質量均為m的木板A、B連接組成如圖所示的裝置，靜置于水平地面上，A板在上，B板在下。現用一個豎直向下的恒力F將木板A緩慢壓到P點，撤去F后，A向上運動，在以后的運動過程中能使B板恰好離開地面。求在這過程物體A上升的位移。

【評析】

本節課的教學重點是幫助學生習得解決輕彈簧關聯物的位移問題的問題圖式。

在環節一中，學生嘗試自己解決同類型中的兩道習題，并在教師的引導分析下，學生從中經歷了正確解決該類問題的思路和方法。心理學家認為，要在頭腦中形成一定的圖式，至少要學習兩個圖式的例子。所以在環節一中，本文選擇了兩道同類型的例子（壓縮-壓縮和拉伸-壓縮）讓學生練習。

在環節二中，通過方法教學，學生從中觀察、思考，有意義地掌握此類問題解決的方法;接著通過提問，讓學生對問題的本質結構特征進行分析，為學生形成解決此類問題的圖式做準備;最后在黑板呈現此類問題的圖式，學生更為深刻地習得解決此類問題的圖式。

在第三環節中，在學生習得此類問題的圖式后，給予學生一定量的同類卻不同情境的問題進行圖式的運用，促進該類問題的圖式儲存在學生的長時記憶系統中。

四、結語

問題圖式作為一種知識結構，能幫助學生有效解決特定類型的物理問題。學生如果習得解決特定類型問題的方法，那么在面對同一類的新問題時，能在識別出問題的本質結構特征后，有比較明確的思路引導，進而一步一步地解決問題。然而，在沒有習得該類型問題的圖式的情況下，學生在面對該領域的新問題時，首先要分析解題的思路，但是這種情況下解決問題的效率是很低的，甚至有可能一步也解決不了。所以在教師的教學過程中，根據問題具有的一些結構特征進行歸類，注重幫助學生構建問題圖式，并引導學生對圖式進行運用，從而脫離題海。

參考文獻：

[1]尹嘉宇，吳春生.物理學科核心素養之解決問題指向性培養——彈簧類問題的特點及解決方法[J].牡丹江教育學院學報，2016（03）：118-119.

[2]皮連生.智育心理學[M].北京：教育科學出版社，2000.

[3]陳剛，朱曉波.論科學課程問題解決的教學[J].教育科學研究，2011（05）：57-60.

[4]謝柳.基于問題圖式的物理問題解決障礙診斷及對策研究[D].華東師范大學，2012.

[5]廖元錫，龍志明.物理問題解決過程的兩種思維方式——問題表征和圖式[J].湘潭師范學院學報（自然科學版），2001（04）：94-98.

[6]陳剛，舒信隆.問題圖式在物理問題解決教學中的應用[J].課程.教材.教法，2009，29（07）：57-61.

作者簡介：林慧金（1995——）女，漢族，廣東茂名人，單位：廣東省深圳市新安中學（集團）外國語學校，碩士，中學二級教師，研究方向：物理教學。