復合固體推進劑顆粒填充模型及其統計特性分析*

顏小婷，夏智勛，那旭東，沙本尚

(國防科技大學 空天科學學院, 湖南 長沙 410073)

固體火箭發動機具有成本低、結構簡單、可靠性高等特點，在火箭和導彈中均有廣泛應用。固體推進劑是固體火箭發動機的主要能量來源，其燃燒特性可顯著影響固體火箭發動機的性能。固體推進劑的燃燒特性會同時受到外部燃燒環境和內部細觀結構的影響，從細觀角度研究各種因素對固體推進劑燃燒特性的影響，找出各種因素之間的制約關系，不僅可以掌握改善和提高推進劑燃燒性能的方法，還可以對推進劑配方的設計提供建議，大大降低推進劑配方研制的成本和危險。

當對體積足夠大的復合固體推進劑進行空間平均分析時，推進劑的化學性質和物理性質均趨于一致。然而，從細觀角度上來講，復合固體推進劑中氧化劑顆粒和金屬顆粒在基體中隨機分布，會造成局部不均勻。推進劑宏觀尺度上的燃燒特性和力學特性與推進劑成分組成、粒徑分布以及細觀尺度上的顆粒排列均密切相關，如燃燒速率、金屬團聚或彈性模量等均在一定程度上由細觀結構形態控制[1]。要分析細觀結構對推進劑性質的影響，首先要對推進劑的細觀結構有一個直觀詳細的認識。目前可采用的試驗手段包括光學分析方法[2]、微型計算機電子掃描(microComputer Tomography, micro-CT)[3-5]和X射線斷層攝影術(X-ray Computed Tomography, XCT)[6-7]等。由于試驗方法耗時長、成本較高，且得到的推進劑細觀結構不易直接用于后續計算分析，需要建立一個能夠描述給定成分組成的推進劑異質細觀結構顆粒填充模型，以此來預測推進劑特性。

利用數值算法生成顆粒填充模型的相關研究始于20世紀50年代，其所仿真的對象不僅限于固體推進劑，還包括瀝青、混凝土、土壤等任意顆粒填充系統[8]，目前已成功實現三維填充模型的顆粒形狀包括球體、橢球體、圓柱體以及各種多面體等[9]。表1對目前已有的部分顆粒填充模型進行了分類總結。復合固體推進劑填充體積分數較大且顆粒多采用多級配粒徑分布，因此采用分子動力學方法更為普遍。Lubachevsky等首次提出了事件驅動的并行顆粒隨機裝填算法，也被稱為LS算法[12]。之后又對算法進行了改進，使其可以用于二維圓盤顆粒和三維球狀顆粒的隨機裝填[13]。由于LS適應性比較強，許多學者以其為基礎發展了自己的顆粒填充模型[14-22]。本文所研究的對象為復合固體推進劑，因此采用的是事件驅動的分子動力學方法。本文工作是之后固體推進劑細觀燃燒模型和鋁團聚模型的基礎。與顆粒粒徑和顆粒質量分數相比，顆粒形狀對推進劑燃燒性能的影響相對較小，因此模型中所有顆粒簡化為球體。

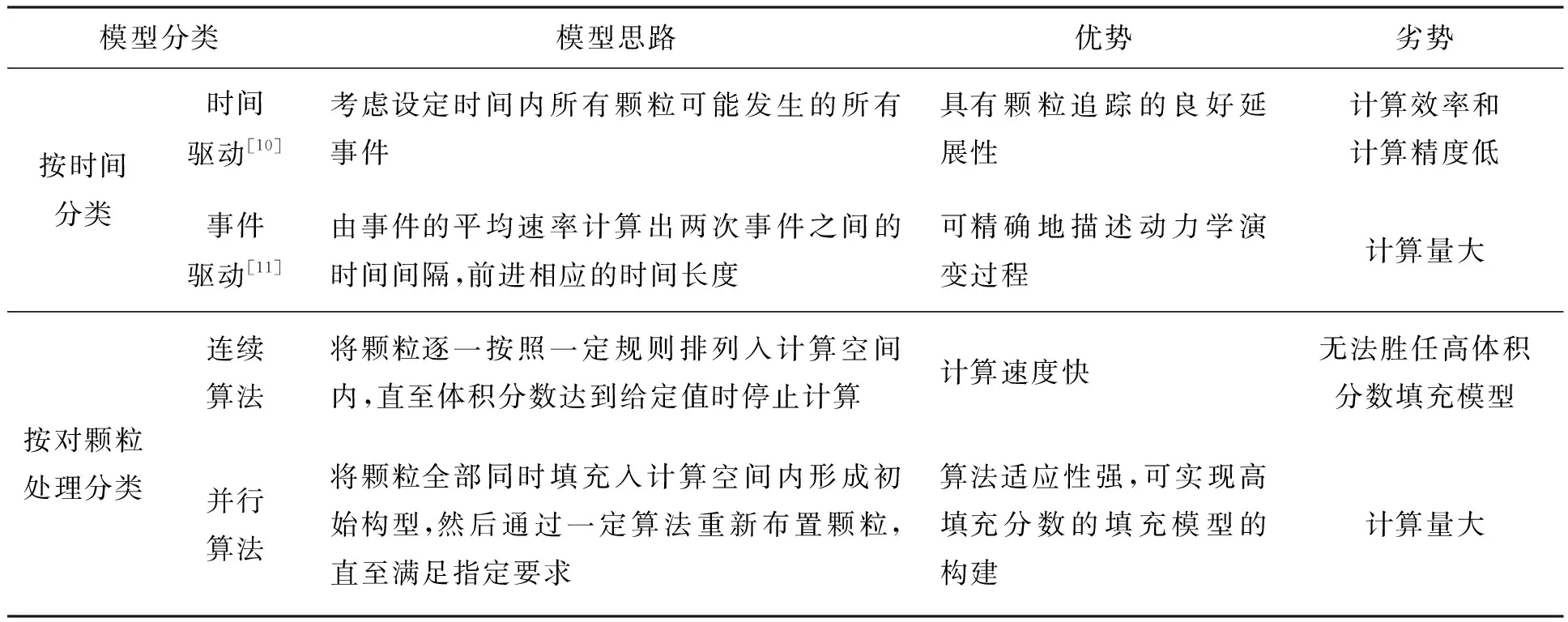
表1 顆粒填充模型分類

利用顆粒填充模型得到的推進劑細觀結構常用于后續對推進劑的燃燒性能或力學性能相關研究。然而，由于結構中顆粒數目大、計算量驚人，無法直接利用與實際試驗所用尺寸相同的顆粒堆積體來進行數值計算。因此，研究者通常利用顆粒堆積體的代表體元(Representative Volume Element, RVE)來進行后續研究。此時，可以認為作為研究對象的復合材料的微結構為周期性結構，即為代表體元的重復性排列，代表體元必須可以在統計意義上代表整個顆粒堆積體，即與顆粒堆積體具有相同的統計相關函數值。顯然，代表體元的尺寸越大，計算結果越準確，然而所需的計算成本也越高。因此，研究者必須要在保證計算精度的前提下找到尺寸最小的代表體元。

材料微觀結構的統計相關函數的量化對于其結構、特性等相關研究非常重要，不同統計相關函數可以定義特定類別的無序材料的材料特性[23]，還可以用于計算異質推進劑的局部密度波動的固有長度，進而研究其對燃燒不穩定的影響[24]。Smith等對復合材料的統計特性進行了長期研究。起初的研究對象為由基體和單一半徑顆粒組成的二維可穿透同心殼(Penetrable-Concentric-Shell，PCS)模型[25]，研究了顆粒不同滲透性下兩點函數與兩點距離和顆粒體積分數之間的關系。之后對單分散球體進行了拓展，針對“最近顆粒表面”建立了“最近表面分布函數”[26]。Hlushkou等[27]研究了三種不同粒徑分布的顆粒填充結構的統計特性，計算得到多分散硬球隨機填充結構的擴散系數。Lochmann等[28]研究了四種不同顆粒粒徑分布的隨機填充結構的統計特性，發現顆粒粒徑分布對于結構的幾何特性和統計特性具有較大影響。Kumar等[29]使用Rocpack生成了固體推進劑的微觀結構，通過對一點和兩點概率函數的計算描述了其統計形態，并引入增強模擬退火對周期單元內的顆粒位置進行了優化。Collins等[30]同樣利用Rocpack生成固體推進劑微觀結構并對其一點、兩點和三點概率函數進行了研究，研究非線性過程時，更高階統計可以對材料給出更精確的描述。

本文采用分子動力學方法，以硝酸酯增塑聚醚(Nitrate Ester Plasticized Polyether, NEPE)固體推進劑作為研究對象，生成了三維球狀顆粒的隨機填充結構體。利用Monte-Carlo方法對顆粒填充結構體的兩點相關函數進行了計算，研究了細觀特性對顆粒填充結構體的統計特性的影響。此外，基于得到的兩點相關函數計算了不同顆粒相的最小RVE尺寸，進而得到了該NEPE固體推進劑的最小RVE尺寸，為后續NEPE固體推進劑細觀燃燒模型相關研究提供基礎。

1 復合固體推進劑顆粒填充幾何模型

1.1 算法基本原理

NEPE推進劑由基體、氧化劑顆粒和金屬顆粒構成，其中氧化劑顆粒和金屬顆粒在基體中隨機分布。在利用分子動力學生成推進劑顆粒填充模型過程中，首先將氧化劑顆粒和金屬顆粒的中心隨機分布在基體內建立初始構型，然后給定顆粒速度和粒徑增長速度，其中粒徑增長速度與顆粒粒徑成正比。采用分子動力學算法計算基體內顆粒運動、顆粒間碰撞以及顆粒變大過程。隨著顆粒粒徑不斷增大，顆粒體積分數不斷上升，最后達到給定體積分數。顆粒粒徑增大和顆粒運動會導致顆粒間碰撞的發生，從而使得顆粒位置不斷調整，以避免出現顆粒重疊的情況。當顆粒體積分數到達給定體積分數時，計算停止，生成給定配方的推進劑顆粒填充模型。由此可見，分子動力學顆粒填充算法的核心問題是預測顆粒間的碰撞時間和碰撞后顆粒運動速度的改變量。所有顆粒被簡化為球形顆粒進行處理。

由于顆粒在基體中隨機分布，顆粒的初始位置和初始速度可以由隨機數發生器隨機給出。在初始時刻指定顆粒所占基體體積分數為1%，根據配方顆粒粒徑分布來給定顆粒初始粒徑。指定顆粒i的直徑為di，粒徑增長速度為ai，則t時刻該顆粒的粒徑為di(t)=ait,(t>di0/ai)，顆粒狀態變量為S(t)=(Ri(t),Vi(t))，其中Ri(t)和Vi(t)分別為顆粒i的顆粒中心位置和運動速度。根據分子動力學算法基本原理可以看出，顆粒初始狀態對最終形成的推進劑顆粒填充模型的細觀結構會有所影響，初始狀態不同，最終形成的推進劑細觀結構也不同，但是不會影響后續從宏觀上對推進劑屬性的分析和計算。

在從宏觀角度研究推進劑特性時，可將整個復合材料視為代表性體積單元的周期性堆積。由于顆粒的運動與初始位置都是隨機的，可能會出現顆粒越過RVE邊界的情況，此時需要給出邊界的顆粒施加周期性邊界條件。對于D維問題，認為其周邊有3D-1個計算域與其相鄰，計算域邊界設置為周期性邊界，具有可穿透性，以此來確保填充模型體積分數的一致性和顆粒個數的恒定性。

1.2 NEPE推進劑顆粒填充幾何模型構建

研究對象為NEPE推進劑，其主要成分粒徑分布及質量分數如表2所示。其中黏合劑包括25%的聚乙二醇(PolyEthylene Glycol, PEG)和75%的塑化劑，塑化劑主要成分組成為50%的硝酸甘油(NitroGlycerin, NG)和50%的1,2,4-丁三醇三硝酸酯(ButaneTriol TriNitrate, BTTN)。

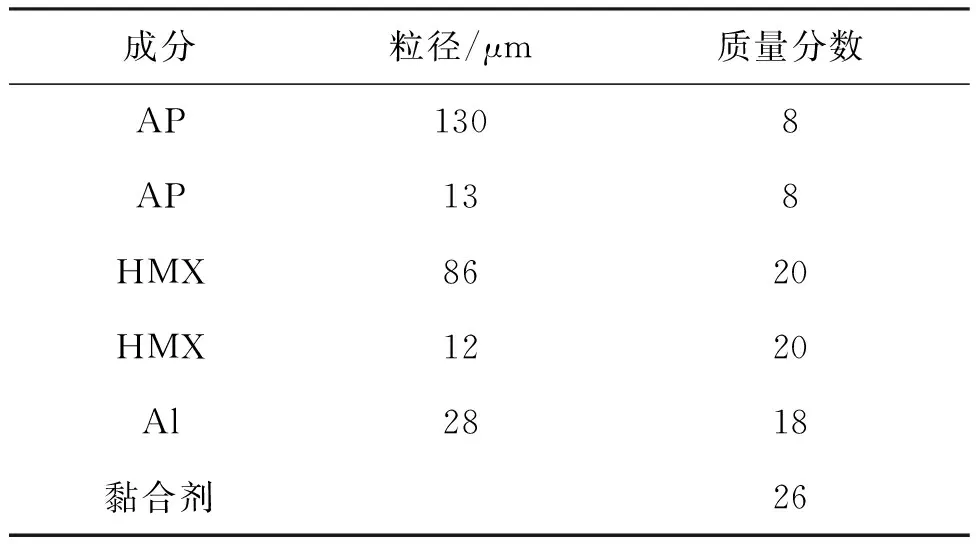
表2 NEPE推進劑主要成分粒徑分布及質量分數

利用上文介紹的顆粒填充算法，根據所給配方和給定基體尺寸計算生成各顆粒的個數，計算得到NEPE推進劑的顆粒填充結構體。由于顆粒粒徑之間差距較大，為了提高計算效率，生成兩種不同邊長的推進劑填充體用來分別計算不同粒徑顆粒相的兩點相關函數。實際生成的NEPE推進劑結構體邊長分別為400 μm和1 000 μm，各相的顆粒個數和體積分數見表3。

表3 NEPE推進劑顆粒填充結構體顆粒組成及體積分數Tab.3 Composites and volume fraction of NEPE propellant pack

由于填充體中顆粒個數須為整數，無法保證不同邊長填充體中各顆粒相體積分數完全相同，在此研究中近似認為生成的兩填充體中同種顆粒相的體積分數相同。圖1給出了構建的邊長為400 μm的顆粒填充結構體的三維模型。其中，紅色顆粒分別代表AP130和AP13，藍色顆粒分別代表HMX86和HMX12，白色顆粒代表Al28。

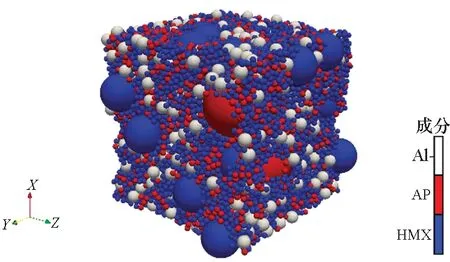
圖1 NEPE推進劑顆粒填充結構體Fig.1 Pack of NEPE propellant

圖2 掃描電子顯微鏡下NEPE推進劑表面形態Fig.2 Surface morphology of NEPE propellant observed by the scanning electron microscope (SEM)

圖2給出了在掃描電子顯微鏡下觀察到的NEPE推進劑的表面形態，可以看出，顆粒隨機分布在基體內且整體分布均勻，小顆粒可均勻分布于大顆粒之間，顆粒所占體積分數較高。這說明利用顆粒填充模型生成的顆粒填充體可以較好地體現出實際推進劑的細觀結構。為了更準確直觀地驗證計算結果的準確性和可行性，在表4中將利用顆粒填充模型計算得到的顆粒體積分數與文獻[5]中通過微計算機斷層掃描技術重構丁羥推進劑細觀結構得到的顆粒體積分數進行對比。對比結果顯示，本文建立的細觀填充模型與實際推進劑的顆粒體積分數誤差較小，主要誤差來自于細觀填充模型無法考慮推進劑中可能存在的孔隙。

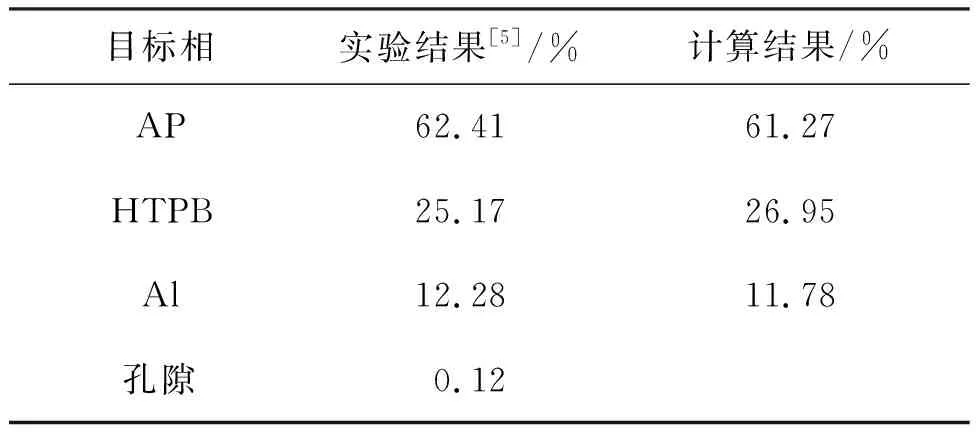
表4 丁羥推進劑二維斷層圖像[5]與細觀填充體中各組分體積含量對比Tab.4 Comparison of the volume fraction of each component between the two-dimensional tomographic image of butyl hydroxide propellant [5] and the pack

2 復合固體推進劑細觀結構統計特性分析

2.1 兩點概率函數及其Monte-Carlo模擬

給定顆粒條件和顆粒堆積體的邊長時，顆粒隨機填充模型可以有多種實現方式，最終生成N種顆粒堆積構型，所有這些不同的顆粒隨機堆積構型即構成樣本總體Ω，每個構型均為該樣本總體的成員，且空間為ω。從微觀角度來看，樣本總體中每個成員的微結構都與其他成員不同，但同時從宏觀角度考慮則是相同的。宏觀尺度是一種長度尺度，此時材料可被假設為具有平均量的連續結構。因此，可將整體均值定義為集合中所有成員上這些數量的期待值。即當樣本總體中每個成員的概率和概率密度分別為P(ω)和p(ω)時，在填充模型中的x點處的函數F(x,ω)的總體均值可定義為：

(1)

此時為計算F(x,ω)的總體均值，需要計算每個成員的F(x,ω)值來求取平均值，計算量較大，因此可通過引入各態歷經性來簡化求值過程。

各態歷經性的基本假設是樣本總體中任一成員的所有狀態都可應用于樣本總體中的所有成員。由于從宏觀尺度上來講，顆粒填充模型生成的所有構型具有相同的物理性質和化學性質，因此可以認為樣本總體Ω符合各態歷經性假設，樣本成員的體積為Vω。此時，可以通過研究單個樣本成員的體積平均值來得到樣本總體均值，即

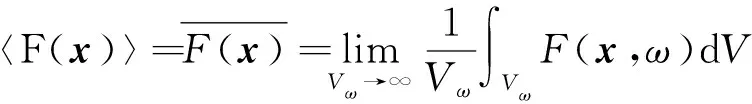
(2)

由于在宏觀尺度下材料可被視為具有周期性結構，因此可利用體積為V0的單個周期單元來計算樣本總體均值，即

(3)

為描述多相顆粒填充模型的統計特性，首先要定義特征函數Iγ(x,ω)。

(4)

即當投點x落入γ相顆粒中時，特征函數取值為1，否則取值為0。

根據前文，其總體均值可由式(5)計算得到。

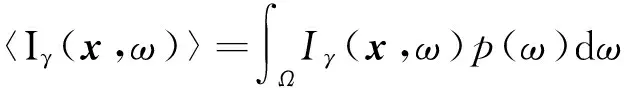
(5)

n點相關函數可以用來研究異質顆粒填充模型的微觀結構的統計特性，其定義式可表示為：

(6)

即n點相關函數等于n個點x1，x2，…，xn隨機投入空間時分別同時處于γ1，γ2，…，γn相的概率。通常來說，n點相關函數很難計算。研究對象僅為顆粒填充模型的幾何參數即代表體單元的長度，不涉及顆粒間作用力對生成的推進劑的力學性質的影響，因此只需研究常用的一點相關函數和兩點相關函數即可。

一點相關函數為最簡單的多點概率統計，計算可得到生成推進劑顆粒填充模型中x點位于γ相的概率，其定義如下：

(7)

引入各態歷經性，則一點相關函數可表示為：

(8)

式中，φγ為顆粒填充模型中γ相所占體積分數。

兩點相關函數計算得到的是推進劑模型中兩點x1，x2分別同時位于γ1相和γ2相的概率，其定義為：

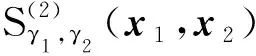
(9)

根據兩點相關函數的定義，在極端條件下兩點相關函數滿足以下取值式：

(10)

(11)

其中，δγ1,γ2為克羅內克符號(Kronecker symbol)，即

(12)

x12趨于0時，兩點趨于一點。由于同一點不可能同時位于兩個不同相內，因此γ1和γ2為不同相時，兩點相關函數取值為零；γ1和γ2為相同相時，兩點相關函數轉變為一點概率函數問題。x12趨于無窮時，由于兩點之間距離足夠大，此時x1和x2具有統計獨立性，兩點相關函數取值為常數，與兩點坐標及相對位置無關。

由于一點相關函數和兩點相關函數較難直接計算，通常采用Monte-Carlo積分方法對其進行估算，即利用無窮和來近似積分。因此一點相關函數和兩點相關函數可分別由式(13)、式(14)計算。

(13)

(14)

由上文可知，兩點相關函數值會隨兩點之間距離增大最終收斂趨近于φγ1φγ2。本文目的在于得到最小周期單元體的尺寸，當隨機選取兩點x1和x2的兩點相關函數值與φγ1φγ2足夠接近時，可以認為尺寸不小于此時兩點距離的推進劑顆粒填充模型與宏觀推進劑在幾何統計角度上具有相同特性。由于算法生成的推進劑顆粒填充模型具有各向同性，周期單元體的最小尺寸在各個方向具有相同值。因此，Monte-Carlo方法的實施主要通過在顆粒填充模型中多次置入距離為rd的兩點來進行，通過計算不同rd下的兩點概率函數來得到周期單元體的最小尺寸。

為了兼顧計算效率和計算精確性，采用介于投針方法和采樣模板(Sampling Template, ST)方法之間的偽投針方法，即在顆粒填充模型中首先隨機選取點x1作為球心，然后隨機給出N2組天頂角θ和方位角φ，以rd作為半徑在球面上隨機選取N2個點作為x2，該過程重復進行N1次。對x1的取值施加邊界限制，若x2位于顆粒填充體之外，則對其相應坐標施加周期性邊界條件以保證計算結果的完整性。

2.2 NEPE推進劑細觀結構統計特性及其RVE最小尺寸

根據上文可知，在極端條件下兩點相關函數取值僅與兩點所在兩相的體積分數相關，為兩相體積分數之積。因此可以將該值作為收斂值，隨著兩點距離增加，兩點相關函數的值會逐漸趨近于該收斂值。當兩點相關函數值與收斂值的誤差始終小于5%時，認為其達到收斂值，此后兩點之間距離繼續增大對于兩點相關函數的值不再有影響。達到收斂值時的兩點之間距離則為對應顆粒相具有統計均勻性的微觀結構的最小代表體元尺寸。所有顆粒相的最小代表體元尺寸的最大值即為該顆粒填充體的最小代表體元尺寸。

3 兩點相關函數計算結果及影響因素分析

3.1 取樣次數和球面取點數

研究對象為六相體，具有21個不同的兩點相關函數，由于整體來說不同的兩點概率函數具有相同的分布趨勢，僅數值不同，因此這里只給出AP13-AP13的兩點概率函數作比較。

圖3給出了球面取點數N2均為100時不同N1下的兩點相關函數，宏觀來看曲線基本重合。圖4給出了5次試驗下兩點相關函數的標準差，可以看出，標準差隨N1的增大逐漸降低，當N1取50 000時，標準差基本比較穩定，并始終處于較低水平。

圖3 N2為100時的兩點相關函數Fig.3 Two-point correlation function when N2 is 100

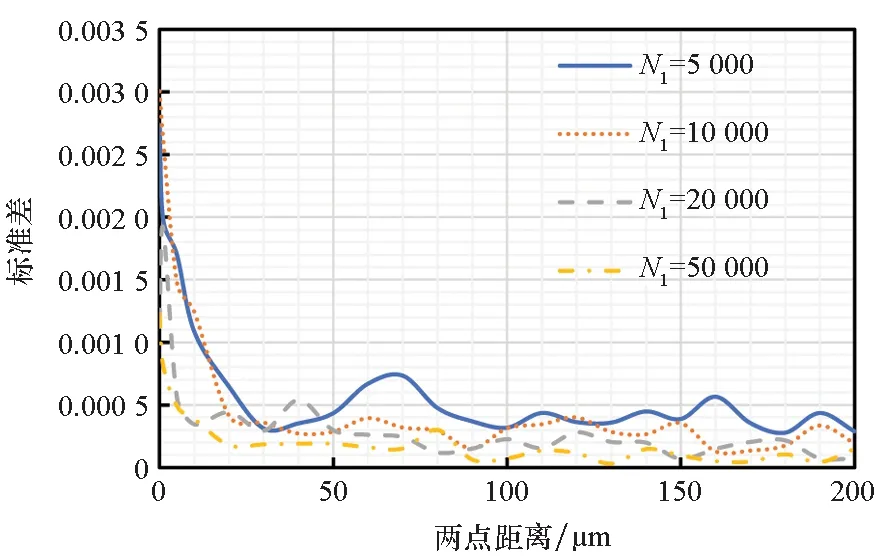
圖4 N2為100時兩點相關函數的標準差Fig.4 Standard deviation of two-point correlation function when N2 is 100

圖5和圖6給出了取樣次數為50 000時，不同N2下的兩點相關函數及標準差，可發現此時N2對取值準確度的影響已基本可以忽略。N1取50 000時，無論N2如何取值，兩點相關函數達到穩定值以后標準差始終低于0.000 5。因此，為同時保證計算精度和計算效率，在本文中取樣次數N1和球面取點數N2分別取50 000和25。

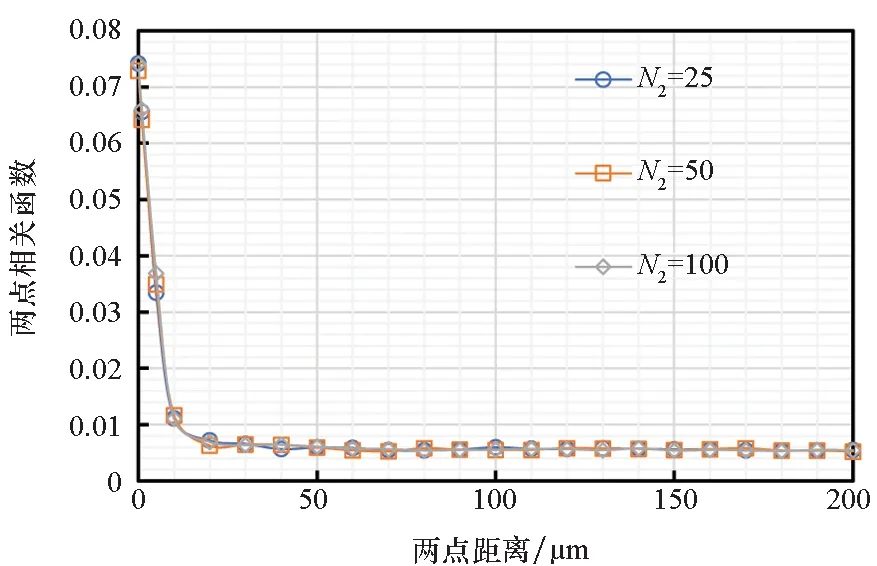
圖5 N1為50 000時的兩點相關函數Fig.5 Two-point correlation function when the N1 is 50 000

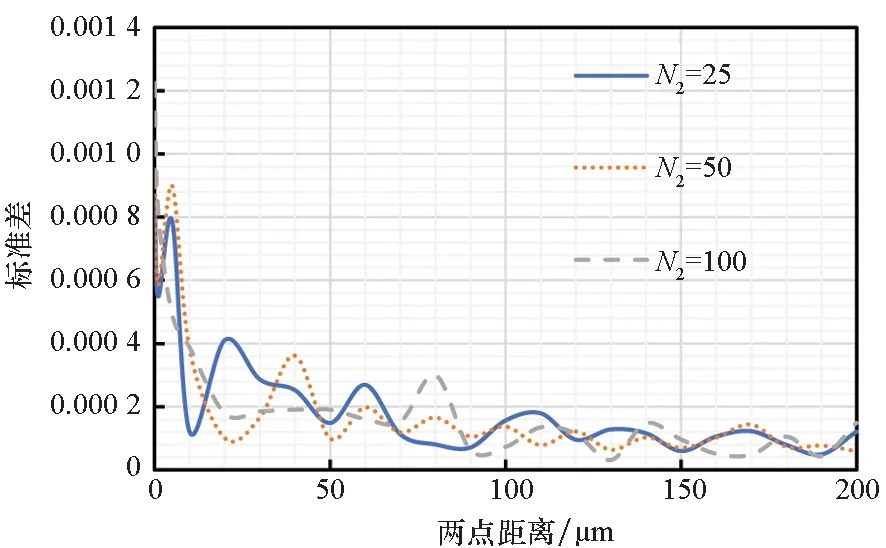
圖6 N1為50 000時的兩點相關函數的標準差Fig.6 Standard deviation of two-point correlation function when the N1 is 50 000

3.2 顆粒粒徑

顆粒體積分數相同時，顆粒粒徑越大，個數越少。圖7和圖8分別給出了HMX12和HMX86的兩點相關函數和標準差隨兩點距離的變化情況，為提高計算效率，HMX12的兩點相關函數利用邊長為400 μm的填充體進行計算。

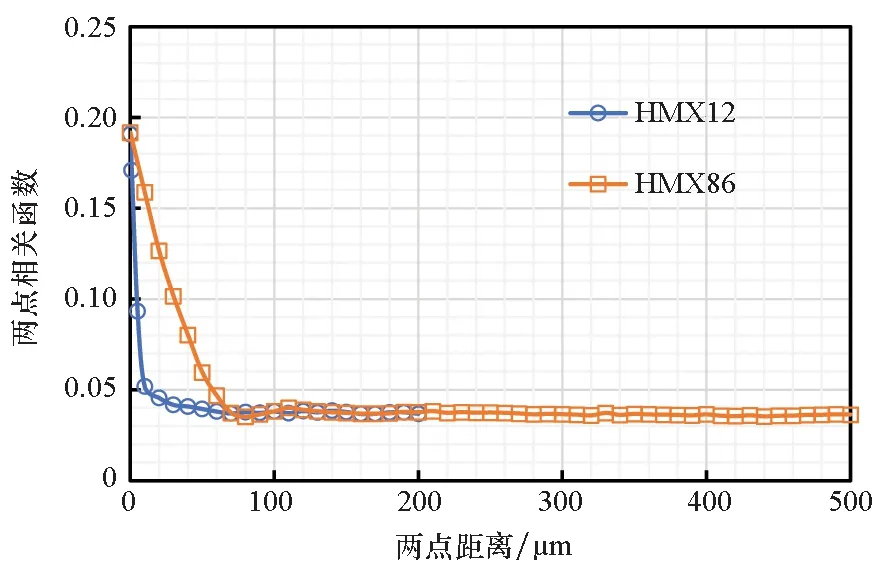
圖7 HMX12和HMX86的兩點相關函數與兩點距離的關系Fig.7 Two-point correlation function as a function of rd of HMX12 and HMX86

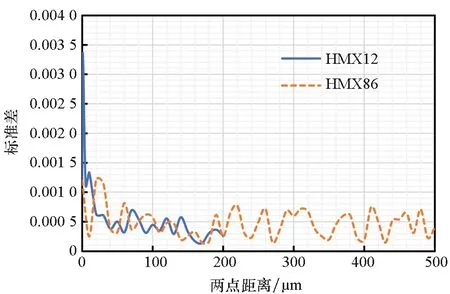
圖8 HMX12和HMX86的兩點相關函數的標準偏差與兩點距離的關系Fig.8 Standard deviation of two-point correlation functions as a function of rd of HMX12 and HMX86

由圖7～8可以發現，顆粒體積分數相同時，兩種顆粒的兩點相關函數收斂于相同值，粒徑小的顆粒的兩點相關函數達到收斂時所需兩點之間的距離更小。由于兩種顆粒個數不同，用變異系數(Coefficient of Variation, CV)來比較數據的離散程度。HMX12和HMX86的變異系數隨兩點距離的變化情況如圖9所示，標準差和變異系數隨兩點距離與顆粒粒徑比的變化情況分別如圖10、圖11所示。

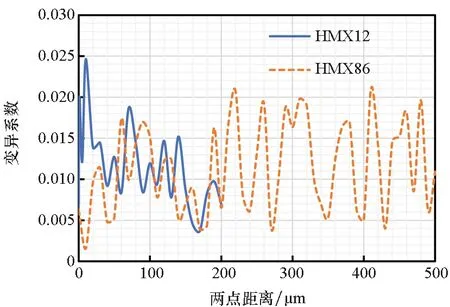
圖9 HMX12和HMX86的變異系數與兩點距離的關系Fig.9 Coefficient of variation comparison of two-point correlation functions as a function of rd of HMX12 and HMX86

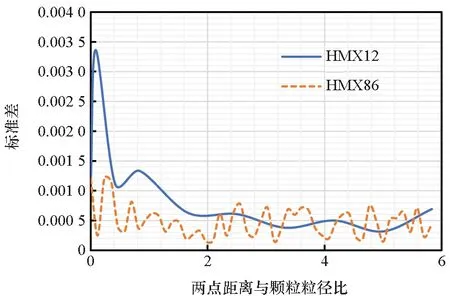
圖10 HMX12和HMX86的兩點相關函數的標準差與兩點距離與顆粒粒徑比的關系Fig.10 Standard deviation of two-point correlation functions as a function of rd/d of HMX12 and HMX86

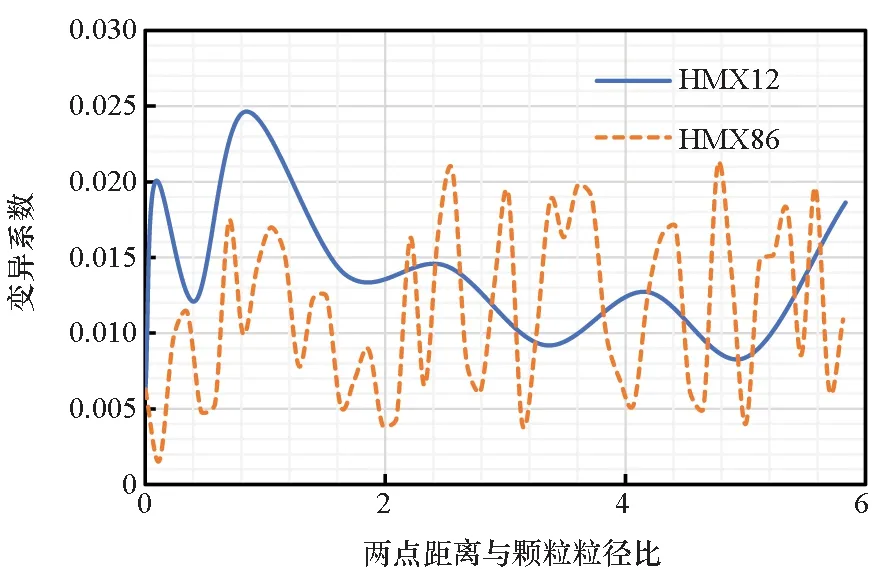
圖11 HMX12和HMX86的變異系數與兩點距離與顆粒粒徑比的關系Fig.11 Cofficient of variation comparison of two-point correlation functions as a function of rd/d of HMX12 and HMX86

N1和N2相同時，從圖9可知HMX12的變異系數似乎低于HMX86。在圖10和圖11，以兩點距離與顆粒粒徑的比值作為橫坐標，可發現在趨于收斂之后兩種顆粒的標準差和變異系數均基本處于相同水平。因此可認為，兩種顆粒體積分數相同時，其顆粒粒徑對于N1和N2的選取沒有什么影響。

圖12給出了HMX12和HMX86的兩點相關函數相對于收斂值的誤差，可看出HMX12的兩點相關函數更快達到收斂。為更直觀地觀察達到收斂值時兩點之間的距離，選取局部圖進行放大，如圖13所示。通過觀察和計算可得到在此推進劑填充模型中HMX12的代表體元尺寸為60 μm，HMX86的代表體元尺寸為300 μm。即體積分數相同時，粒徑小的顆粒所需的RVE尺寸更小。

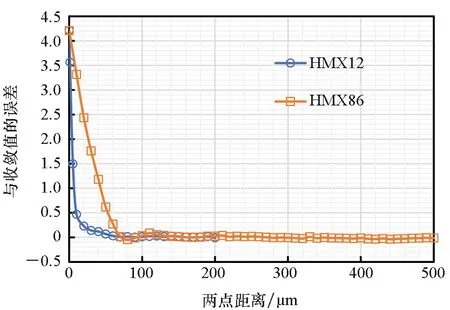
圖12 HMX12和HMX86的兩點相關函數關于收斂值的誤差Fig.12 Error between two-point correlation function and convergence value of HMX12 and HMX86

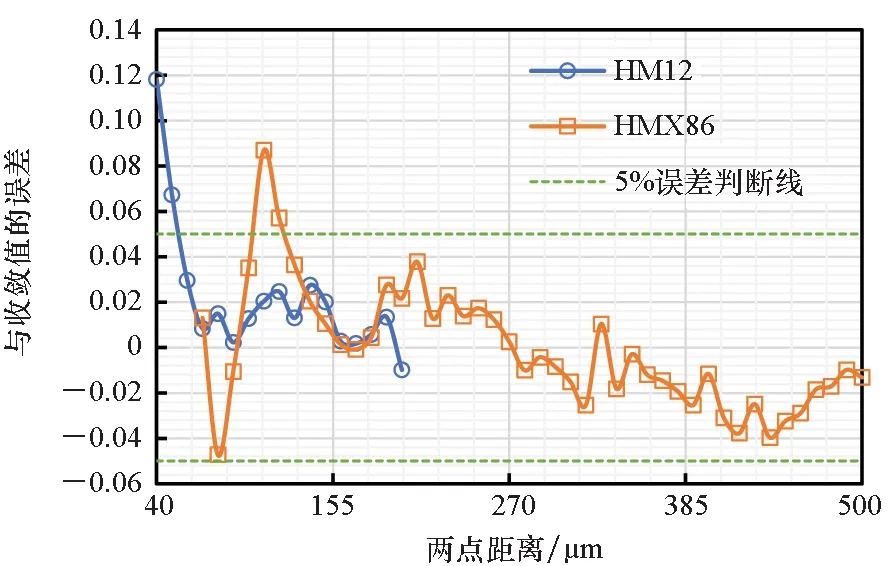
圖13 HMX12和HMX86兩點相關函數關于收斂值誤差的局部放大圖Fig.13 Error comparison between two-point correlation functions of HMX12 and HMX86 and the convergence value within a certain range

3.3 顆粒體積分數

圖14比較了AP13和HMX12的兩點相關函數，可以發現在粒徑相近時，兩種顆粒收斂的速度近似相同，需要分別計算其最小RVE尺寸才能發現體積分數對其的影響。圖15給出了AP13和HMX12的變異系數隨兩點距離的變化情況。從圖15可發現，AP13的變異系數基本上均大于HMX12，說明當顆粒粒徑相同時，其在顆粒填充體內所占體積分數越大，利用Monte-Carlo方法計算其兩點相關函數時所需取點越少。

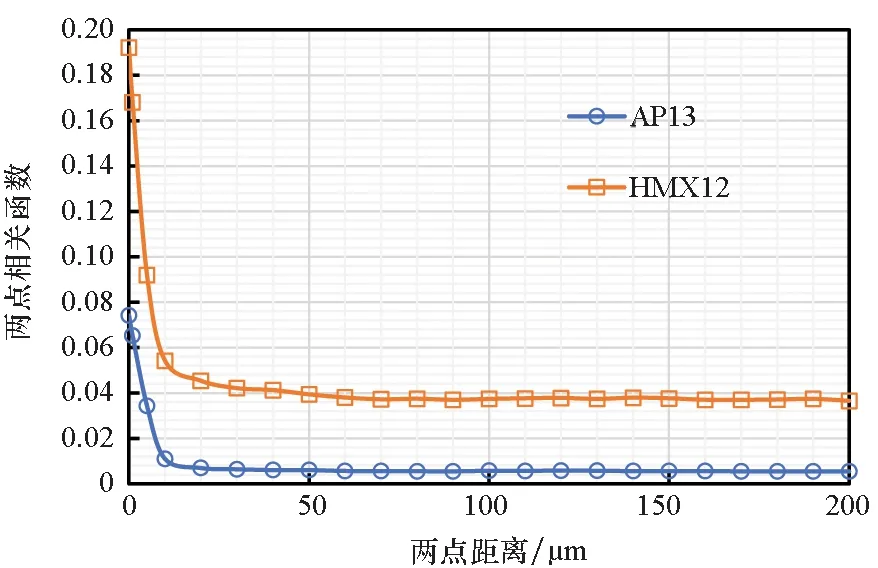
圖14 AP13和HMX12的兩點相關函數Fig.14 Two-point correlation functions of AP13 and HMX12

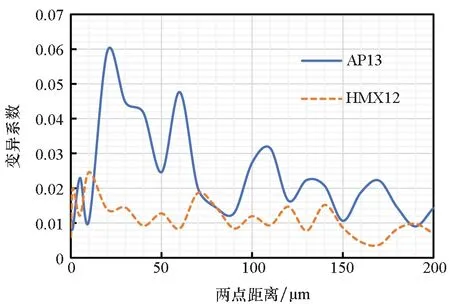
圖15 AP13和HMX12的變異系數Fig.15 Coefficient of variation comparison of two-point correlation functions of AP13 and HMX12

圖16給出了AP13和HMX12的兩點相關函數值對于收斂值的誤差，根據2.2節給出的RVE最小尺寸判斷依據可看出，AP13和HMX12均可選取60 μm作為其代表體元尺寸，由于AP13和HMX12的粒徑較小，這種結果可能是由取點不夠密集造成。因此，在兩點距離50～70 μm之間重新密集取點計算兩點相關函數及其相對于收斂值的誤差，進而計算AP13和HMX12的代表體元尺寸。圖17為圖16的局部放大圖。根據RVE最小尺寸判斷依據，由圖17可得，HMX12在兩點距離為54 μm時達到收斂，AP13在兩點距離為60 μm時達到收斂，且AP13相對于收斂值的誤差波動更大。說明顆粒粒徑相近時，體積分數越大，其代表體元長度越小。

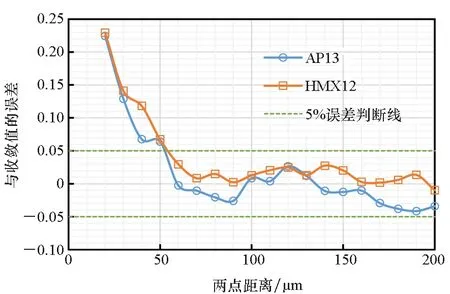
圖16 AP13和HMX12的兩點相關函數關于收斂值的誤差Fig.16 Error comparison between two-point correlation functions of AP13 and HMX12 and the convergence value

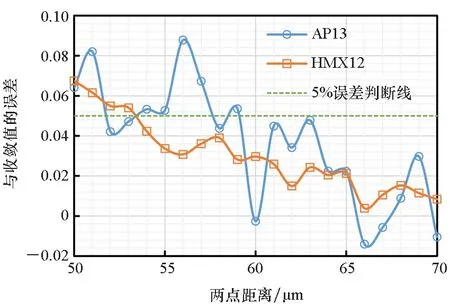
圖17 AP13和HMX12的兩點相關函數關于收斂值誤差的局部放大圖Fig.17 Error comparison between two-point correlation functions of AP13 and HMX12 and the convergence value within a certain range

3.4 不同顆粒粒徑分布

圖18給出了兩種顆粒相的三個兩點相關函數的分布，圖19比較了這三個兩點相關函數的變異系數。可以發現，AP130-AP130的變異系數最大且波動較大，HMX86-HMX86的變異系數始終處于較低水平且相對平緩，AP130-HMX86的變異系數基本處于二者之間。

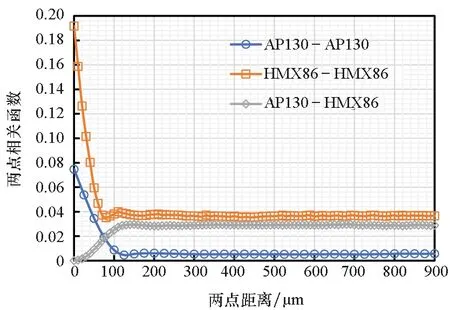
圖18 AP130-AP130，HMX86-HMX86和AP130-HMX86的兩點相關函數Fig.18 Two-point correlation functions of AP130-AP130, HMX86-HMX86 and AP130-HMX86

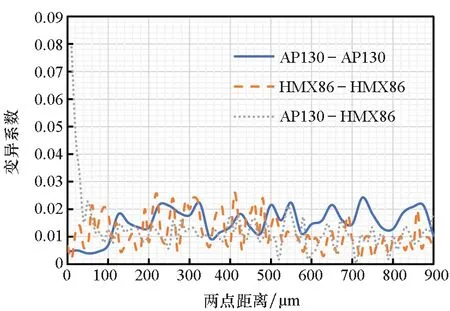
圖19 AP130-AP130，HMX86-HMX86和AP130-HMX86的變異系數Fig.19 Coefficient of variation comparison of two-point correlation functions of AP130-AP130, AP130-HMX86 and AP130-HMX86

圖20給出了這兩種顆粒相的三個兩點相關函數關于收斂值的誤差。可發現，在給定兩點長度內，兩點相關函數已達到較好收斂效果。為了更清晰地比較不同兩點相關函數收斂速度及其最小代表體元尺寸，圖21通過對數據范圍進行篩選對圖20進行了放大。根據RVE最小尺寸判斷依據可得出AP130-AP130的最小代表體元尺寸為750 μm，HMX86-HMX86的最小代表體元尺寸為130 μm，AP130-HMX86的最小代表體元尺寸為120 μm。由此可推，對于多級配模型，不同顆粒相的兩點相關函數比單顆粒相的兩點相關函數收斂更快，其最小代表體元尺寸比兩種單顆粒相的最小代表體元尺寸小。

圖20 AP130-AP130，HMX86-HMX86和AP130-HMX86的兩點相關函數關于收斂值的誤差Fig.20 Error between two-point correlation functions of AP130-AP130, HMX86-HMX86 and AP130-HMX86 and the convergence value

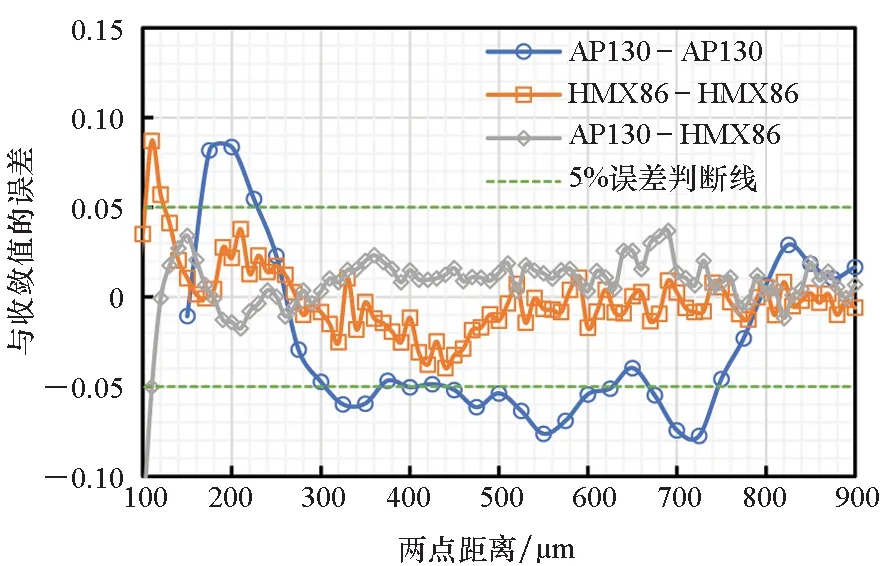
圖21 AP130-AP130，HMX86-HMX86和AP130-HMX86的兩點相關函數關于收斂值誤差的局部放大圖Fig.21 Error comparison between two-point correlation functions of AP130-AP130, HMX86-HMX86 and AP130-HMX86 and the convergence value within a certain rangee

4 結論

本文利用基于分子動力學的復合固體推進劑顆粒填充模型，以NEPE固體推進劑為研究對象，生成了指定成分的NEPE推進劑的顆粒填充體。為了得到顆粒填充體的最小代表體元尺寸，為之后對于推進劑燃燒特性的研究提供模型基礎，基于Monte-Carlo理論，采用偽投針方法對顆粒填充體的統計特性進行了研究。研究發現：

1)兩種顆粒體積分數相同時，其顆粒粒徑對于投點次數的選取幾乎沒有影響，但是對最小代表體元尺寸有較大影響。體積分數相同時，最小代表體元尺寸與顆粒相直徑具有直接關系，直徑越大，實現統計均勻性所需的兩點距離越大。

2)當顆粒粒徑固定時，其在顆粒填充體內所占體積分數越大，利用Monte-Carlo方法計算其兩點相關函數時所需取點的次數越少。當顆粒相直徑相近時，顆粒在填充體中體積分數越大，實現統計均勻性所需的兩點距離越小，即其最小代表體元尺寸也越小。

3)對于多級配粒徑分布模型，分別位于不同顆粒相的兩點相關函數比對應的兩種單顆粒相的兩點相關函數收斂更快，即多級配顆粒的最小代表體元尺寸要小于對應單顆粒的最小代表體元尺寸。為保證計算精度，顆粒填充體的最小代表體元尺寸應不小于填充體內所有顆粒相的最小代表體元尺寸中的最大值。因此，在實際應用中，可考慮只計算單顆粒相的最小代表體元尺寸，其中的最大值即可用作該顆粒填充體的最小代表體元尺寸。