基于ANN的新型MOFs性能預測①

賴 欣,盧 罡,王 磊,畢志遠,陽慶元,俞度立,4

1(北京化工大學 信息科學與技術學院,北京 100029)

2(北京化工大學 信息科學與技術學院 智能無人系統研究中心,北京 100029)

3(北京化工大學 有機無機復合材料國家重點實驗室,北京 100029)

4(北京化工大學 軟物質科學與工程高精尖創新中心,北京 100029)

近年來,以機器學習、深度學習為代表的人工智能理論和方法受到人們的廣泛關注.尤其是谷歌DeepMind 團隊開發的AlphaGo,在圍棋領域中的精彩表現令人印象深刻[1,2].在此之后,DeepMind 又迅速對計算機視覺等領域做出了可喜成果[3].如今,機器學習已被廣泛應用于自然語言處理[4,5]、數據挖掘[6]、證券市場分析[7]、機器人應用[8,9]、醫學診斷[10,11]等領域.

在材料科學領域,材料的各種反應、合成中會產生海量的數據,而將善于從海量數據中發掘規律的機器學習方法應用于材料科學領域便順理成章[12,13].實驗研究發現,由于MOFs 具有較高的孔隙率和具有規律性、可組合性、多元性等特點,能夠高效地通過計算機模擬預測MOFs 材料的物理化學性質[14].通過GCMC (Grand Canonical Monte Carlo)分子模擬方法對MOFs 進行高通量篩選已經被證實是一種有效的實驗手段[15,16].目前應用的分子模擬方法主要有分子動力學、蒙特卡羅、密度泛函理論等.在探尋物理化學性能優秀的MOFs 材料過程中,需要對材料的結構特性、物理性質、化學性質等進行搜索分析,通常可以應用GCMC 分子模擬方法.然而,可能存在的MOFs結構存在于一個近乎無窮大的樣本空間,要將所有MOFs 材料逐一進行分子模擬計算,從而挑選出性能出眾的材料,其計算成本是無法估量的.近年來,人們已經開始關注如何在準確預測MOFs 性能基礎上,提高計算效率.Simon 研究組將少量MOFs 吸附材料放入綜合數據庫中,對其進行GCMC 模擬,找出吸附材料的物理結構特性與其對CH4吸附能力之間的關系[17].其中用到的MOFs 數據有Zeolites[18]、hypothetical MOFs(hMOFs)[19]、Porous Polymer Networks (PPNs)[20]、hypothetical Zeolitic Imidazolate Frameworks (hZIFs)[21]以及Computation-Ready Experimental (CoRE) MOF[22]等MOFs 材料數據.材料數據包含多種性質特征,利用機器學習挖掘其定量構效關系(Quantitative Structure-Property Relationship,QSPR)[23],可將這些結構性質作為參數,對材料分子的氣體吸附能力進行回歸分析和預測.Fernandez 等通過晶體學的RDF 分析方法,利用RDF 得分評估MOF,同時利用多元線性回歸、支持向量機等方法,構建了處于不同壓力環境下,MOFs 材料針對CO2、N2與CH4的氣體吸附與RDF得分的QSPR模型[24].之后,Fernandez 小組利用孔隙率和孔徑等物理結構變量,預測MOFs對CH4的吸收,并在實驗中得到R2=0.85的結果[25].Fernandez 等還應用了分類方法,基于QSPR預測表現最佳的CO2吸附MOFs 材料,達到94.5%的準確率[26].Sezginel 等經過QSPR 分析,提出一種多變量線性模型,利用該模型與MOFs的結構特性,包括表面積、晶體密度、孔隙率、孔徑以及等量熱吸附(Qst),預測出MOFs 吸附劑對CH4的吸收能力,實驗結果發現,孔隙率與等量熱吸附是影響MOFs 氣體吸附能力的關鍵因素[27].Chung 等利用遺傳算法,對捕獲CO2的MOFs進行篩選,在計算效率上獲得了50 倍左右的提升[28].這些工作在材料篩選效率上有著出色的表現.

本文工作受到Chung 等2016年關于遺傳算法(Genetic Algorithm,GA)方面工作[28]的啟發.他們在材料數據庫中通過遺傳算法進行材料篩選,但是對于遺傳算法生成的庫中沒有的新個體并未進行進一步的評估.本文用原始MOFs 數據集訓練人工神經網絡(Artificial Neural Network,ANN),并用ANN對遺傳算法生成的新型MOFs 個體的性能進行預測評估,從而搜索對CH4氣體具有較高吸附性的MOFs.我們首先通過GCMC 模擬計算文獻[28]中數據集的每個MOFs在一定條件下對于CH4氣體的吸附性能,然后用該結果訓練一個ANN,使其能夠評估和預測MOFs 基因與CH4氣體吸附性之間的構效關系.實驗結果表明,基于ANN 搜索并預測的材料吸附性能平均表現優于原始材料數據庫中的最優材料,證實了該方法的可行性和有效性.

1 面向GA和ANN的MOFs 數據集

1.1 針對MOFs 材料數據進行基因編碼

為了通過GA 搜索新型MOFs,需要根據MOF的特征設計GA 所需的基因編碼.為MOFs 進行基因編碼的方式沒有特定的規則,但應能夠盡量反映MOFs的結構特征及各組分、配體之間的組合特征,從而在GA 運行過程中,基因編碼的變化能夠反映出MOFs 組合結構的變化.

本文的原始數據來自于WLLFHS hMOF 數據集[19].該數據集中MOFs的參數由Wilmer 研究組匯編和驗證,具有豐富多樣的MOFs 材料結構,適合進行分子模擬篩選與機器學習分析.文獻[28] 將該數據集中的MOFs 進行基因編碼,該編碼利用6 個整數作為“基因”,每個“基因”都表示了一種分子的特性或者功能[28].本文沿用該基因編碼,具體設定如下:

第1 位基因,表示潛在互穿能力,共4 種,用0 至3的整數表達;第2 位基因,表示實際互穿能力,共4 種,用0 至3的整數表達;第3 位基因,表示無機配體,共5 種,用0 至4的整數表達;第4 位基因,表示主要有機連接單元,共40 種,用0 至39的整數表達;第5 位基因,表示次要有機連接單元,共40 種,用0 至39的整數表達;第6 位基因,表示化學官能團,共15 種,用0 至14的整數表達.

根據上述設定,MOFs 材料的搜索空間大小為:4×4×5×40×40×15=1920 000.在這種編碼方式下,構象異構體之間以及只有官能團定位不同的MOFs 之間具有相同的基因編碼.Chung 等[28]分析發現,構象異構體之間、只有官能團定位不同的MOFs 之間不僅結構類似,化學性能也相當.因此,他們從類似的MOFs中選擇一個作為代表,縮減數據集的規模.最終,文獻[28]整理了具有51 163 個MOF 基因編碼的數據集.

1.2 計算對CH4 氣體的吸附值

在文獻[28]整理的數據集基礎上,我們進一步采用自主開發的力場參數和自主研發的模擬計算軟件,通過GCMC 模擬計算其中每個MOFs在298 K (K為開爾文,熱力學溫度單位,下同)條件下對CH4氣體的吸附能力.

MOF 材料和氣體分子之間的相互作用采用范德華力(vdW)和庫侖勢的組合來表示[29].其中范德華力采用Lennard-Jones (LJ)方程描述.LJ 勢能參數取自UFF 力場,CH4分子勢能參數取自TraPPE 力場.不同原子之間的LJ 勢能參數采用Lorentz-Berthelot 混合規則計算.

在前期的研究工作中,我們利用量子密度泛函和Monte Carlo 模擬相結合的跨尺度手段開發出了新的力場[30],其中基于量子力學層次的密度泛函理論(Density Functional Theory,DFT)[31]計算被用于確定材料與氣體分子之間的精確相互作用參數.DFT 計算基于Materials Studio 軟件中的Dmol3 模塊,采用GGA 交換泛函Perdew-Burke-Ernzerhof (PBE)和含軌道極化函數的雙數值軌道基組(DNP),并結合Grimme的色散校正作用(DFT-D2),對MOF 中獲取的模型簇進行優化,并計算出不同距離下無機單元與CH4之間的相互作用能.在此基礎上,通過Monte Carlo 模擬實現了MOFs對CH4氣體在298 K 條件下吸附量的量化,計算得到了數據集中每個MOF對CH4氣體的吸附值.

本文基于自主研發的模擬計算軟件HT-CADSS(http://jshx.buct.edu.cn/yjcg/bzxcg/86799.htm),采用GCMC 方法研究了298 K 條件下,文獻[28]的數據集中51 163 個MOFs對CH4氣體的吸附能力.在GCMC 模擬中,采用Peng-Robinson (PR)方程將壓力轉換為逸度作為計算的輸入值.所有的MOFs 均視為剛性材料,并在三維尺度上采用周期性邊界條件.計算范德華作用的截斷半徑(cut-off)設置為1.4 nm.對于每一個吸附模擬過程,模擬總步數為3000 萬步,前1500 萬步用于系統平衡,后1500 萬步用于獲得熱力學性質的統計平均值.對CH4單組分吸附模擬,涉及分子的平移、插入和刪除.在無限稀釋條件下,MOF 骨架與氣體分子之間相互作用力的相對強弱采用無限稀釋吸附熱進行表征.無限稀釋吸附熱采用基于正則系綜(NVT)的Widom測試粒子方法[32]計算.

經過以上的計算,最終得到51 163 個經過基因編碼的MOFs對CH4氣體的吸附值,最大為528,其基因編碼為2-0-0-29-29-12.數據示例如表1所示.

表1 數據示例

1.3 單特征分析

1.1 節中,一個MOF 被編碼成了一個具有6 個基因的染色體,6 個基因分別代表了它的6 個結構特征.本節中,我們分別分析了這6 個特征與MOFs的CH4氣體吸附能力之間的構效關系,結果如圖1所示.

圖1(a)為MOFs 潛在互穿能力與MOFs對CH4氣體吸附能力的關系.WLLFHS 數據庫以材料結構的多樣性著稱,因此,具有不同潛在互穿能力的MOFs在CH4氣體吸附能力上分布較為均勻,體現了該數據集中樣本的多樣性和完整性.圖1(b)顯示了在實際互穿能力的維度上,數據集中MOFs對CH4氣體吸附能力的分布.可以看到,實際互穿能力越高的MOFs對CH4氣體吸附能力相對越差.這是由于互穿較多的MOFs穩定性較高,一定程度上阻礙了氣體分子的吸附[33].對于圖1(c)中的無機節點而言,帶有鋅或銅槳輪與對位連接的MOFs,在分析結果中表現出更強的CH4氣體吸附性能,這是由于部分MOFs 材料在活化的過程中,遇金屬簇配位溶劑分子或水分子易脫落,形成不飽和金屬位點,從而增強了對CH4氣體的吸附作用.另外,研究表明,當MOFs 材料與水接觸時,結構的結晶性會在一定時間內消失.大多數情況下,水的存在是不可避免的,具有二價金屬離子(例如Zn2+和Cu2+)的MOF在有水的情況下極易出現這種不穩定性[34,35].主有機連接單元與次有機連接單元對MOFs的CH4氣體吸附性能的影響分別如圖1(d)和圖1(e).可以看到,表現良好的有機連接單元主要集中在12-30 號區間內,而31-39號有機連接單元在低性能MOFs 中缺失.圖1(f)顯示,含有0 號、7 號、10 號、12 號化學官能團的MOFs 材料對CH4氣體吸附能力突出,其中0 號表示不考慮官能團影響,其余3 種官能團分別對應甲基、乙基、丙基[28].我們認為,這是因為這類烴基官能團與CH4有相似的機構和化學性質.

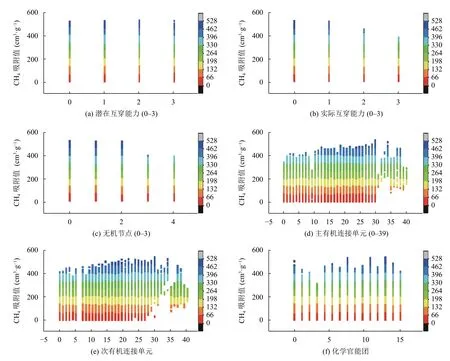
圖1 各基因編碼與CH4 氣體吸附能力的構效關系

對于單特征的分析表明,MOFs對CH4氣體吸附能力受多種因素共同作用影響,包括MOFs 材料的拓撲結構、有機配體和無機單元的結構、官能團的選擇等.單純的針對其中某一方面進行修改,并不能保證有效提升MOFs 材料對于CH4氣體的吸附能力.這也進一步體現了應用包括ANN在內的機器學習方法發掘這種非線性構效關系的意義.

2 ANN 模型的訓練

對于GA 產生的新型MOFs 個體,從僅有的6 個基因位點的值構建MOF 結構,再生成相應的數據進行GCMC 模擬計算,從而進行性能評估,將是一個非常繁瑣及耗時的過程.因此我們提出將MOFs的基因編碼作為輸入,GCMC 模擬計算的目標性能作為輸出,訓練ANN 作為挖掘MOFs 構效關系的機器學習模型,從而能夠對GA 生成的新的MOFs 個體進行性能預測評估.

2.1 ANN 模型評價指標

ANN 通過模仿人類大腦的思維方式,進行大規模高維數據處理和分析.一個ANN 包含輸入層、隱含層和輸出層,其中隱含層可以有多層.ANN的本質是非線性函數映射,通過對高維數據的低維非線性映射,轉變為人類可理解的結果輸出.由于需要預測MOFs對CH4氣體的吸附值,因此我們將ANN 構建為輸出層只有一個神經元的回歸神經網絡,從而輸出一個實數值.作為預測具體數值的回歸ANN,其評價指標R2的值越接近1,模型的預測性能越好,其定義如下:

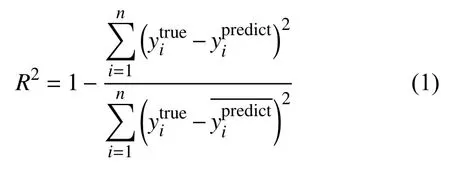
其中,n是測試集中MOFs 個體的數量,為第i個MOFs 結果的預測值,是通過GCMC 模擬得到的結果.是所有的平均值.另一個評價指標均方誤差(Mean Square Error,MSE),是預測值和真實值之間誤差的平方和,其定義為:

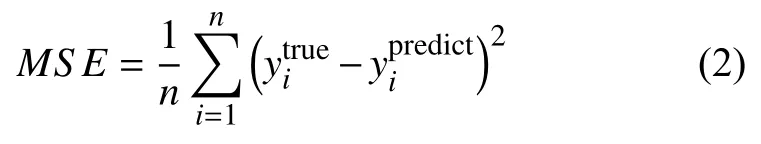
2.2 數據集準備

對1.2 節生成的數據集中51 163 條MOFs 數據的CH4氣體吸附值以20為長度進行區間劃分,進而對數據的分布情況進行初步統計,結果如圖2所示.統計結果顯示,在該數據集中,存在極少數CH4氣體吸附值大于480的MOFs.這種數據分布的傾斜,會影響模型的學習和預測性能.因此,我們從吸附值大于280的MOFs樣本中隨機重復抽取一定數量的樣本,然后對每一個樣本的吸附值引入以該吸附值為均值、方差為1的高斯隨機誤差.經過這樣的隨機上采樣后,數據集擴充到67 878 條,其分布如圖3所示.

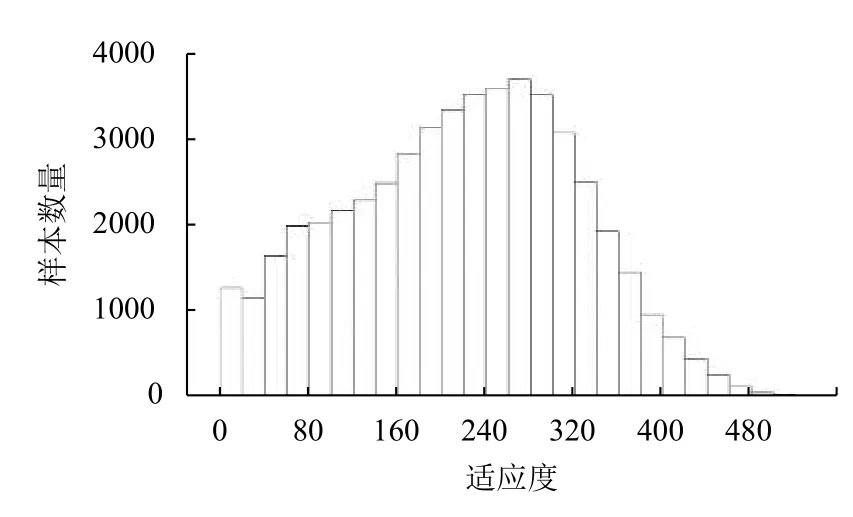
圖2 原始數據集分布直方圖

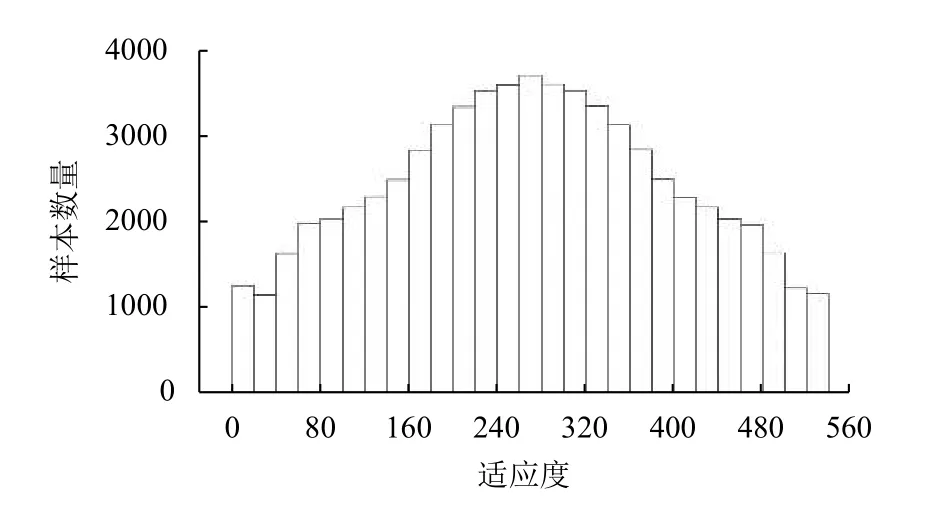
圖3 上采樣后數據集分布直方圖

對經過上采樣后的67 878 條數據的各特征值進行最大最小標準化預處理,以消除數據集不同特征取值范圍不同對模型訓練的影響,并加快模型訓練的收斂速度.最大最小標準化的方法如式(3)所示:

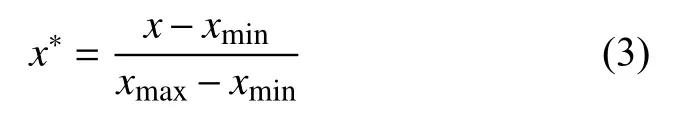
其中,xmax是樣本數據的最大值,xmin是樣本數據的最小值.

經過以上預處理后,我們將所有67 878 條數據隨機抽取80%作為訓練集,剩余20%作為測試集.

2.3 BPNN和RBFNN

本文分別采用BP 神經網絡(Back Propagation Neural Network,BPNN)和徑向基函數神經網絡(Radial Basis Function Neural Network,RBFNN)對GA 生成的新型MOFs 個體進行了針對CH4氣體吸附性能的預測評估實驗.利用BP 神經網絡與徑向基函數神經網絡進行針對CH4氣體吸附性能預測評估的優點主要有:

(1)BP 神經網絡擁有高容錯性,并行計算,自適應和可學習等優點,在針對MOFs 材料吸附CH4氣體能力這類非線性關系的預測方面具有顯著的優勢.

(2)徑向基神經網絡在本文中設置為BP 神經網絡的對照,作為一種性能優秀的前饋型神經網絡,理論上可以逼近任意非線性函數,具有全局逼近能力,從根本上解決了BP 神經網絡由于梯度下降所導致的局部最優問題,且由于其整體網絡結構緊湊,收斂速度快.而BP 神經網絡中權值調節采用負梯度下降法,收斂速度遞減而較慢.

(3)BP 神經網絡學習速率是固定的,因此對于一些復雜問題,BP 算法需要的訓練時間可能非常長,這主要是由于學習速率太小造成的.而徑向基神經網絡是高效的前饋式網絡,它訓練速度相對較快的同時,具有BP 神經網絡所不具有的最佳逼近性能和全局最優特性.

2.3.1 BPNN的構建和訓練

BPNN是ANN 中經典且常見的一種神經網絡.結構上,BPNN 包含輸入層、隱含層和輸出層.其本質是通過對高維數據的低維非線性映射,轉變為人類可理解的輸出結果.由于1.1 節中將MOFs 結構編碼為具有6 個基因的染色體,故本文BPNN的輸入層相應地設置為6 個神經元,對應6 個基因的輸入,而輸出為1 個神經元,用于預測吸附值.在保持較為簡單的網絡結構的前提下,經過多次調整、實驗,最終確定了2 個隱層后增加1 個批歸一化層的基本結構.具體地,隱藏層的激活函數使用ReLU 函數,輸出層以Sigmoid 函數作為激活函數.訓練的epoch 設為100,batch_size 設為128,采用隨機梯度下降(Stochastic Gradient Descent,SGD)迭代訓練模型,并采用Adam 方法進行優化,學習率設為0.002.其中,激活函數是一種神經網絡常用的非線性函數,用于實現對上一層神經元輸出的線性組合進行非線性變換.批歸一化(Batch Normalization,BN)層的Scale and Shift 操作,可以加速訓練過程的收斂、控制過擬合、降低網絡對初始化權重的敏感程度,并允許使用比較大的學習率.

通過用訓練集進行5 折交叉驗證,最終網絡結構調整實驗的結果如表2所示.表中結果按照R2降序排列.可以看到,2 個隱層神經元個數分別為32和15 時的模型準確度最高.BPNN 訓練過程需要調節的參數個數為6 ×32×15+15=2895.

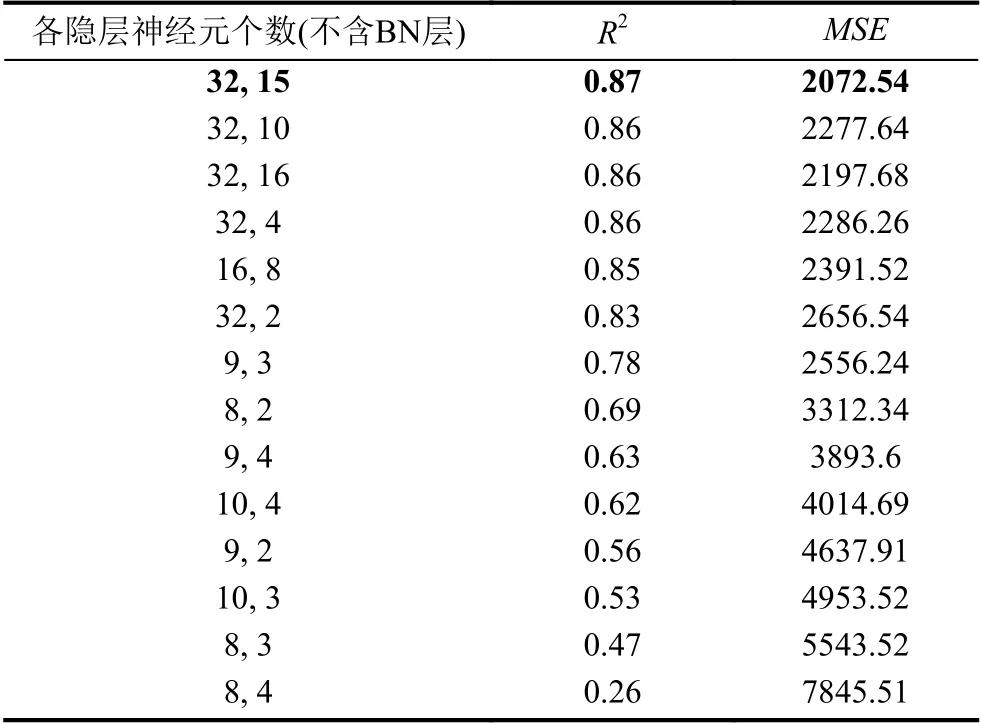
表2 BPNN 結構調節實驗結果

2.3.2 RBFNN的構建和訓練

作為比較,我們還構建了另外一種常見的人工神經網絡——徑向基函數神經網絡.RBFNN是一種前饋型的3 層神經網絡,激勵函數使用徑向基函數.其隱含層中神經元與輸入、輸出層的神經元之間的關系不再是全連接,而是用徑向基函數代替.本文中,采用常用的高斯函數作為徑向基函數.與BPNN 相比,RBFNN通常泛化能力更強,能夠避免BPNN 可能出現的局部最優問題,理論上能夠在充分訓練的情況下完全逼近要擬合的數據.該網絡可以方便地增加神經元進行訓練,直到滿足精度要求為止,這樣的網絡結構擁有更為突出的定向信息處理能力.本文通過調整神經網絡的結構,將隱含層神經元個數從100 個開始,逐次遞增,每次調節增加100 個神經元,觀察評價指標R2與MSE的數值變化情況,從而確定最優的網絡結構.

使用與2.3.1 節相同的訓練集進行5 折交叉驗證,比較訓練結果,得到當隱層節點設置為600 個時,其MSE=2264.83、R2=0.854為最優,即RBFNN的結構確定為6-600-1.調節隱含層神經元個數的比較結果如表3所示.從中可以看到,隱層節點數為800 時,結果與隱層節點數為600的相差無幾,但從模型復雜度、參數數量等角度綜合考慮,最終,選取隱層節點數為600為最合適的網絡隱層節點個數.由于徑向基函數神經網絡是局部逼近網絡,其對于輸入空間的某個局部區域只有少數幾個連接權值影響輸出,故而該網絡實際需要調節的參數數量大大小于BP 神經網絡.

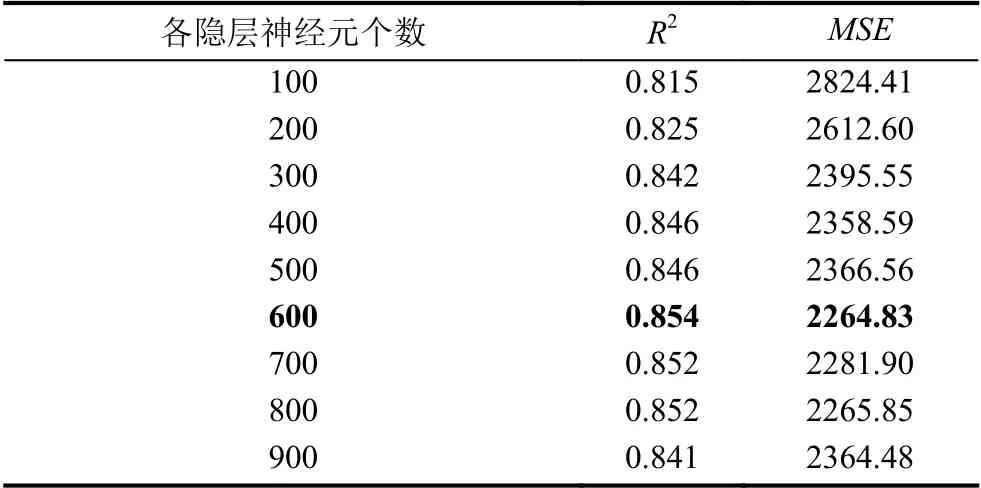
表3 RBFNN 結構調節實驗結果

2.3.3 BPNN和RBFNN的性能比較

通過上述對BPNN和RBFNN 結構的優化,我們分別訓練并確定了BPNN和RBFNN的結構和參數.該過程已經初步顯示了二者的性能.圖4和圖5分別展示了二者在測試集上回歸預測的具體性能表現.

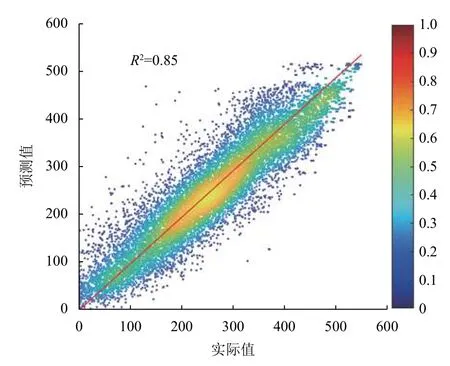
圖4 BPNN 網絡模型在測試集上的回歸散點圖

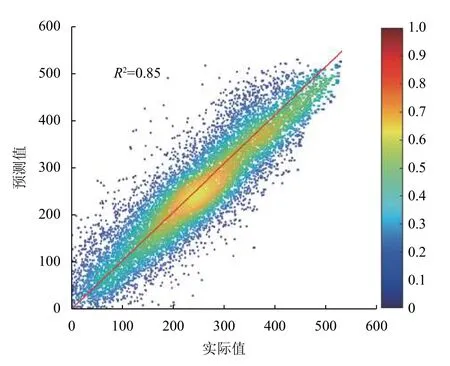
圖5 RBFN 網絡模型在測試集上的回歸散點圖

上述模型回歸結果圖中,顏色表明數據點的密集程度,顏色越接近紅色,數據分布越密集.當實際值與預測值接近時,數據點會均勻分布在紅色標識實線及兩側.從圖4中可以直觀地看出,采用2.3.1 節所得的6-32-15-1 結構的BPNN 時,在測試集上的實驗結果R2=0.85;類似地,RBFN 以2.3.2 節所得的隱層節點數為600 時,其在測試集上得到R2=0.85.可見,兩種模型在測試集上均可以實現較為準確的回歸.這些結果表明基于訓練數據構建的非線性模型具有可以預測新型MOFs 材料氣體吸附性能的能力.

3 實驗結果

基于1.2 節構建的基礎數據集,以及2.2 節對于數據集的處理和劃分,我們應用GA 實現了對MOFs 個體的演化搜索,并應用ANN對搜索到的新型MOFs 進行了基于CH4吸附值的性能預測評估實驗.

3.1 基于GA的MOFs 搜索

GA是一種具有生存與檢測特征、不斷進行迭代過程的一種全局優化搜索算法.在迭代過程中,會產生大量通過基因編碼表示的個體,每個個體的基因特征會隨著進化的進行,根據優勝劣汰的基本原則進行代際遺傳,從而產生優秀個體,實現在搜索空間中對最優解的搜索.

GA的主要參數包括種群規模M、進化代數N、遺傳交叉率a,以及遺傳變異率b.其中,a決定了兩個個體進行交叉操作從而產生新子代的概率,b為一個個體的某個隨機基因發生變異的概率.GA 中的種群規模,代表著數據域內數據點的密度,密度越大,其覆蓋最優解的可能性越高,即對求解最優解越有利.但相應的,其計算量也將會快速增加;對于GA 進化代數的限制,是為了讓算法能夠在合理的實驗時間內完成迭代搜索;GA 中的變異概率與交叉概率設定,是為了讓數據域內的數據點保持相對分散的分布,避免陷入局部最優的困境,文獻[28] 中的設定為＜M=100,N=100,a=0.65,b=0.05＞.此外,適應度函數也是GA的一項重要設定.通過適應度函數,GA 計算個體的適應度,評估個體的性能.適應度越高,種群越朝著有利于發展的方向進化.文獻[28]采取的操作是,在原數據集中查找新生成的個體,若找到,則通過GCMC 模擬方法計算它對CO2的工作容量、CO2/H2的選擇性,以及對CO2的吸附值,分別以這3 個指標作為個體的適應度值以評估個體性能;若新生成的個體不在原數據集中,則重新進行基因操作,直到生成數據集中存在的個體.也就是說,文獻[28]中并未對原數據集中不存在的新個體進行評估并加入新的子代.

本文以1.2 節計算的MOFs對CH4氣體的吸附值F作為適應度,參照文獻[28]中的參數設定,以產生新型MOFs 個體的數量X、搜索到最優個體所進化的代數G,以及搜索到的最優個體吸附值F為評價指標,針對M和N兩個參數進行了6 組參數設定的實驗.具體步驟為:

(1)在原始數據集上構建初始種群.初始種群中的個體可從數據集中進行多次隨機選擇并擇優,也可加入一些人為設定的策略.例如,文獻[28]中人工選擇100 個MOFs 個體構建初始種群,從而保證所設計的每個基因都至少出現一次,個體演化過程中不會有基因的缺失.

(2)執行遺傳算法,開始種群的演化.這個過程包含了遺傳算法中的經典操作,例如從種群中進行個體的擇優、交叉、變異,從而產生下一代種群,不斷迭代,直到算法停止

(3)在GA 迭代演化過程中,對于產生的MOF 個體,如果存在于原數據集中,則直接使用其已經計算得到的目標性能指標值作為個體性能的評估結果,并加入下一代種群;否則將新個體暫存.

(4)算法的停止條件,可以為指定的演化迭代次數、指定的搜索到新的優秀個體數量等.

按照上述實驗步驟不斷循環迭代,本文依據實際實驗條件,綜合考慮遺傳算法的計算效果與計算周期,調整實驗參數,經過6 組實驗最終將遺傳算法參數設定為＜M=50,N=200,a=0.65,b=0.05＞,如表4所示.

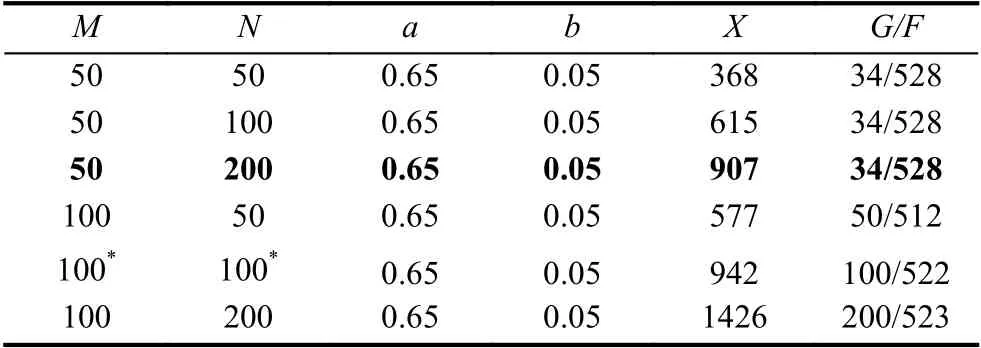
表4 GA 參數組合實驗結果

最終,GA 算法搜索到907 個原數據集中不存在的新MOFs 個體.同時我們觀察到,原始數據集中,第1 個基因(潛在互穿能力)的值均不小于第2 個基因(實際互穿能力)的值.這是因為,潛在互穿能力表示理論上可能的互穿能力,所以實際互穿能力不會超過它.因此,我們將907 個新型MOFs 個體中不符合該條件的144 個刪除,剩余763 個新型MOFs 個體作為實驗對象.

3.2 ANN對新型MOFs 個體的性能預測

本文分別采用前文所述的BPNN和RBFNN對GA 搜索到的763 個新型MOFs 個體進行CH4氣體的吸附值預測,取二者預測的對CH4氣體吸附值最高的前10 位MOFs 個體進行比較,如表5所示.

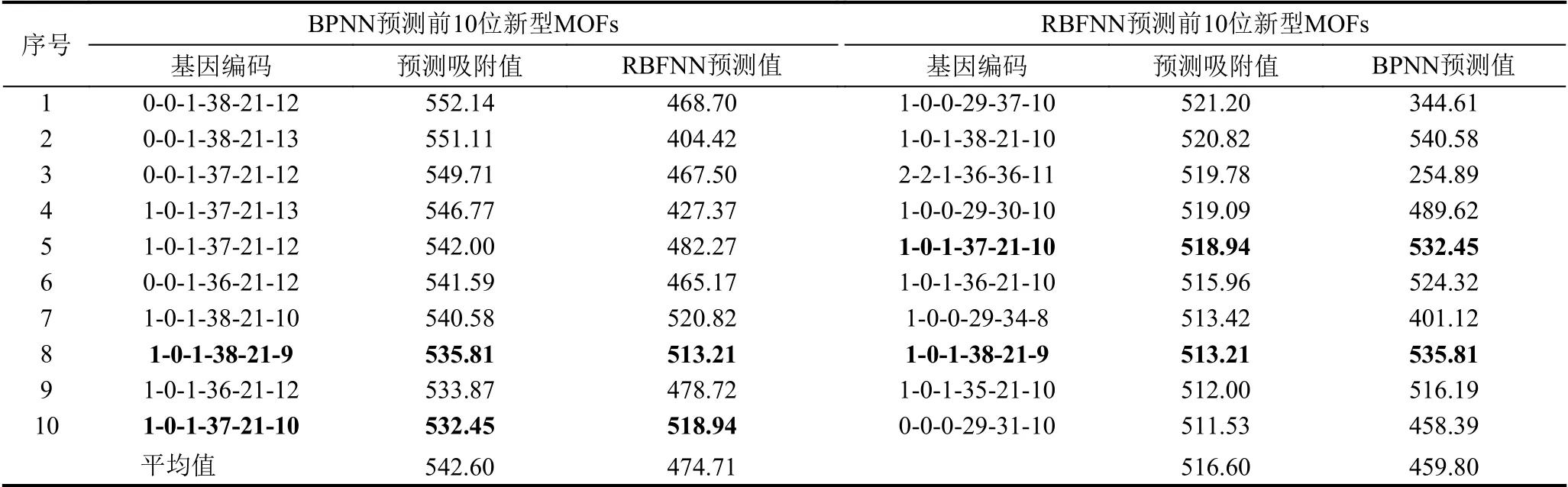
表5 BPNN和RBFNN 分別對新型MOFs 個體的CH4 氣體吸附值預測結果TOP10對比

從兩者結果比較可以看出,BPNN 預測的前10 種新型MOFs 材料,其CH4氣體吸附能力的均值為542.60,略高于RBFNN 預測結果前10 名的516.60.有趣的是,BPNN 預測的前10 位MOFs,對CH4氣體的吸附性能均在530 以上,高于原始數據集內的最大值528,突破了訓練集的限制,具有更好的泛化能力.而RBFNN 預測的CH4氣體吸附值最大為521.20,未能突破訓練集的范圍.從基因編碼的結構上看,BPNN對于結構相近的MOFs 個體,預測的CH4氣體吸附值也較為接近.例如,預測基因編碼結構為0-0-1-38-21-12的CH4氣體吸附值為552.14,與其相近的基因編碼結構為0-0-1-38-21-13的CH4氣體吸附值為551.11.這個結果具有一定的合理性.另一方面,RBFNN的預測結果具有更強的多樣性,得到的高CH4氣體吸附值的基因編碼結構與BPNN 預測得到的有很大不同.

具體地,BPNN 預測得到的高CH4氣體吸附值的MOFs 個體,其潛在互穿性僅限于1 或0,而實際互穿性均保持在0;而RBFNN 預測得到的高CH4氣體吸附值的MOFs 個體,潛在互穿性和實際互穿性均出現了2的取值.對于第3 個基因編碼,BPNN 預測得到的高CH4氣體吸附值的前10 名均為1,而RBFNN的結果中還包含0.根據文獻[28]的補充材料中的設定,該位基因為0和1 所表示的無機配體,如圖6所示.

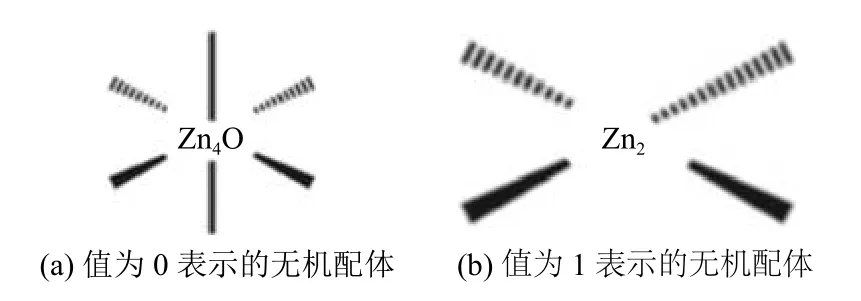
圖6 無機配體的表示[28]

BPNN的結果中,主要有機連接單元出現了36、37、38,而RBFNN的結果中還出現了29和35.第5 位的次要有機連接單元,BPNN 預測得到的結果中均為21,RBFNN的結果中除了21,還出現了30、31、34、36、37.根據文獻[28]的補充材料中的設定,它們表示的結構如圖7所示.

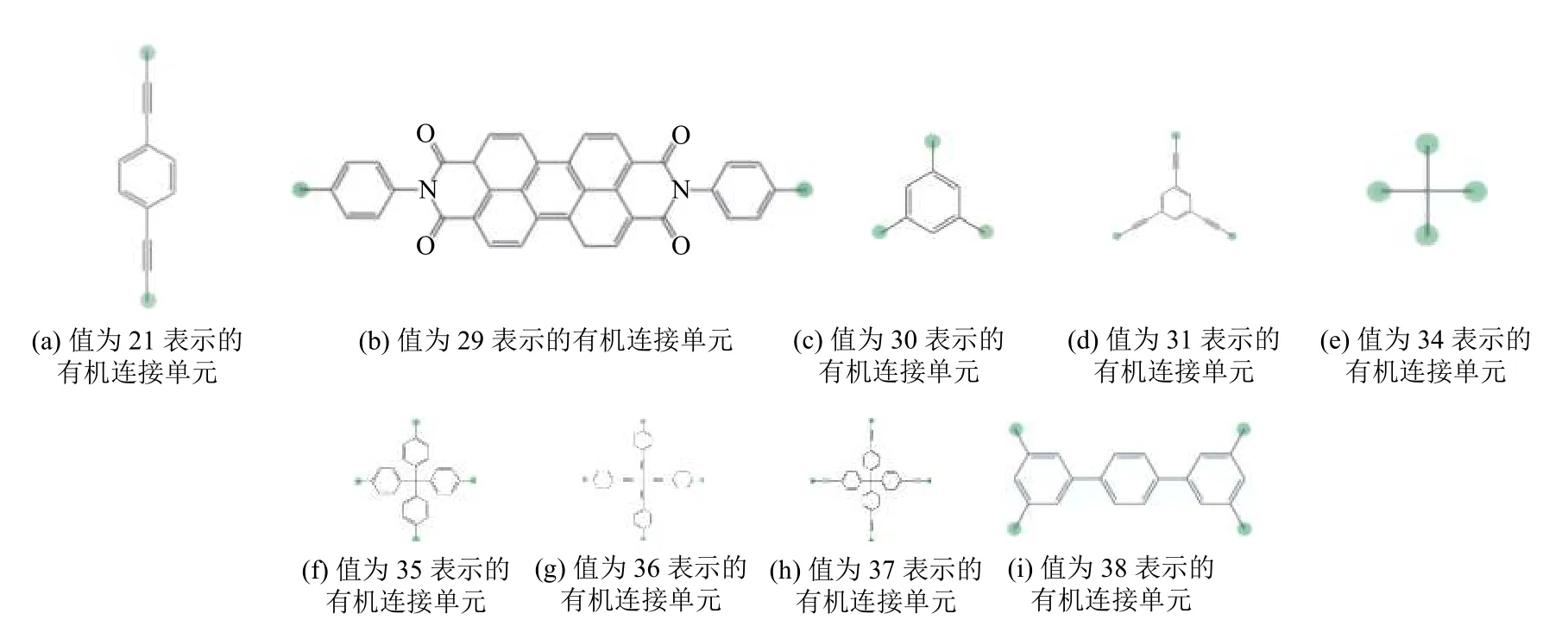
圖7 有機連接單元的表示[28]

最后一位基因值表示的化學官能團,BPNN 預測的結果中出現了9、10、12、13,而RBFNN的結果中則為8、9、10、11.根據文獻[28]的補充材料中的設定,它們表示的結構如圖8所示.

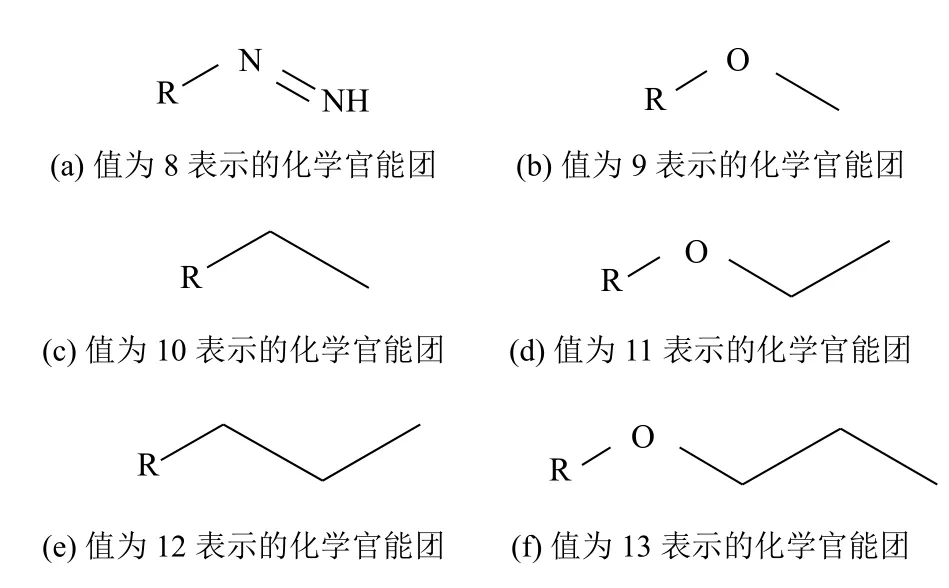
圖8 化學官能團的表示[28]

以上結果表明,特定的幾種結構將給MOFs 帶來較高的CH4氣體吸附值.值得注意的是,BPNN和RBFNN 均預測出1-0-1-38-21-9、1-0-1-37-21-10 結構的MOF 具有相對較高的CH4氣體吸附值,這值得后續的研究工作進一步關注.

4 結論與展望

本文首先根據我們提出的力場參數,基于現有的MOFs 數據集,通過GCMC 模擬計算構建了面向一定條件下CH4氣體吸附能力的MOFs 數據集,并通過上采樣技術調整了數據集的分布.其次,以該數據集分別訓練了BPNN和RBFNN 模型,使其具備較強的預測CH4氣體吸附性的能力.然后,通過GA 基于MOFs 數據庫搜索新型的MOFs 個體.搜索時,對于搜索到的數據集中已有的MOFs,直接查詢數據集中其對應的CH4氣體吸附值;對于搜索到的不在數據集中的新型MOF,則暫存它們.最后搜索出763 個新型MOFs 個體,并分別用訓練好的BPNN 與RBFNN對其CH4氣體吸附性進行預測,得到了優于原始數據集的結果.通過以上過程,實現了通過GA 搜索新型MOFs,并用ANN對其進行性能預測,從而實現高性能MOFs的高效搜索與評估.

實驗結果表明,BPNN在模型的準確性,泛化能力方面略優于RBFNN,而RBFNN 預測結果則更具備多樣性.二者的預測結果均表現出特定的結構對MOF 性能有一定的影響.對于二者均預測出具有較高CH4氣體吸附值的兩種MOF 新型結構,則需要進一步的研究和驗證.

未來可進一步拓展現有工作,從而引入多種機器學習方法作為參照進行比較和相互佐證.對GA 參數更深入的優化研究也是一個有挑戰性的課題方向.同時,可考慮結合實際化學材料領域中的自組裝技術,通過材料組裝,模擬,優化出新材料的分子結構,然后再利用GCMC 手段,添加材料的實際化學特征值數據,完善成果.