一種并行不對(duì)稱空洞卷積模塊①
張智杰,尉 飛,葛青青,趙寶奇,孫軍梅,李秀梅
(杭州師范大學(xué) 信息科學(xué)與技術(shù)學(xué)院,杭州 311121)
卷積神經(jīng)網(wǎng)絡(luò)廣泛應(yīng)用于圖像分類、語(yǔ)義分割和圖像生成等計(jì)算機(jī)視覺領(lǐng)域,其通過(guò)卷積核對(duì)圖像中的局部區(qū)域做卷積,以提取圖像中的特征,在每一層的卷積中通過(guò)參數(shù)共享以減少模型復(fù)雜度,之后結(jié)合池化操作實(shí)現(xiàn)位移不變性的識(shí)別.現(xiàn)有的卷積神經(jīng)網(wǎng)絡(luò)普遍將3×3 卷積作為其基本構(gòu)建模塊.對(duì)于卷積神經(jīng)網(wǎng)絡(luò)而言,卷積核的感受野、深度以及通道數(shù)決定了網(wǎng)絡(luò)的性能.感受野越大,表示特征圖上像素點(diǎn)映射的區(qū)域越大;深度決定了網(wǎng)絡(luò)的抽象能力或?qū)W習(xí)能力;通道數(shù)決定了卷積核所包含的信息量大小.感受野和通道數(shù)共同決定了卷積層學(xué)習(xí)有效信息與空間的能力.
2012年,卷積神經(jīng)網(wǎng)絡(luò)在復(fù)雜模型下的有效性得到證明[1];2015年Inception Net v1[2]以及v2、v3、v4[3]證明了更多的卷積和更深的網(wǎng)絡(luò)可以得到更好的分類效果;2016年,ResNet 解決了深度網(wǎng)絡(luò)結(jié)構(gòu)的訓(xùn)練問題[4].傳統(tǒng)的卷積操作主要有3 個(gè)缺點(diǎn):(1)使用的是局部操作,不能得到比較大的范圍甚至圖像的全局特征,且卷積核是固定的尺寸;(2)對(duì)物體的形狀、姿態(tài)變化缺少適應(yīng)性;(3)當(dāng)特征的通道數(shù)變大后,卷積核的參數(shù)也變得龐大,增加了運(yùn)算量.在傳統(tǒng)的卷積神經(jīng)網(wǎng)絡(luò)中,圖像輸入到卷積神經(jīng)網(wǎng)絡(luò)后,先對(duì)圖像做傳統(tǒng)的卷積,然后進(jìn)行池化操作,通過(guò)降低特征點(diǎn)的數(shù)量來(lái)擴(kuò)大感受野[5].由于圖像分割是像素級(jí)的預(yù)測(cè),對(duì)池化后較小尺寸的圖像上采樣到的原始圖像尺寸進(jìn)行預(yù)測(cè),這種先池化后上采樣的操作使得特征圖的尺寸依次進(jìn)行了縮小和增大,該過(guò)程帶來(lái)了信息的損失.
2015年,空洞卷積被提出,它是在標(biāo)準(zhǔn)的卷積核上注入空洞,以達(dá)到擴(kuò)大感受野的目的.相較于傳統(tǒng)卷積,空洞卷積不僅可以保留數(shù)據(jù)的內(nèi)部結(jié)構(gòu),也可以獲得上下文信息,而且不需要下采樣、池化等操作來(lái)進(jìn)行特征的提取.在WaveNet[6],ByteNet[7]等網(wǎng)絡(luò)中,也用到了空洞卷積,以提升網(wǎng)絡(luò)性能.空洞卷積起源于圖像分割領(lǐng)域,也廣泛應(yīng)用于在分類任務(wù)中[8].空洞卷積避免了池化所帶來(lái)的信息丟失,彌補(bǔ)了上述傳統(tǒng)卷積的3 個(gè)缺點(diǎn)[9],但同時(shí)帶來(lái)了空間層次和信息連續(xù)性丟失等問題.
不對(duì)稱卷積通常用于模型的加速和壓縮.在現(xiàn)有研究中,研究者將n×n的對(duì)稱卷積分解為1×n和n×1 卷積,減少了模型的參數(shù).如果二維卷積核的秩為1,其運(yùn)算可以等價(jià)轉(zhuǎn)換成一系列的一維卷積.在實(shí)際情況中,由于卷積核具有分布特征值,因此卷積核的秩要高得多,直接應(yīng)用會(huì)導(dǎo)致信息大量損失.Denton 等人用奇異值分解[10],找到了一個(gè)低秩逼近,對(duì)上層進(jìn)行精細(xì)化來(lái)恢復(fù)卷積性能.Jaberberg 等人通過(guò)最小化重構(gòu)建誤差,成功學(xué)習(xí)了水平核和垂直核[11].Jin 等人應(yīng)用結(jié)構(gòu)約束使二維卷積可分離,在精度不變同時(shí)使計(jì)算時(shí)間加速2 倍[12].非對(duì)稱卷積也廣泛應(yīng)用于網(wǎng)絡(luò)結(jié)構(gòu)的構(gòu)成,如Inception Net 中,1×7和7×1 卷積代替了7×7 卷積.ENet 網(wǎng)絡(luò)中也采用了不對(duì)稱卷積設(shè)計(jì)網(wǎng)絡(luò),雖然分類效果有所下降,但是模型參數(shù)降低了33%,降低了網(wǎng)絡(luò)的復(fù)雜度[13].
針對(duì)空洞卷積所帶來(lái)的問題,本文提出了一種新的并行不對(duì)稱空洞卷積模塊,用2×2的空洞卷積、1×3和3×1的不對(duì)稱卷積進(jìn)行并列相加,代替原有的3×3 卷積,以增強(qiáng)原有的卷積核.本文主要貢獻(xiàn)如下:
(1)本文提出的并行不對(duì)稱空洞卷積模塊引入了空洞卷積,在不增加參數(shù)的情況下,可以擴(kuò)大感受野,捕獲多尺度上下文信息.
(2)本文提出的并行不對(duì)稱空洞卷積模塊,著重在特定維度尋找特征,補(bǔ)全空洞卷積在空間層次上缺失的信息,使整個(gè)網(wǎng)絡(luò)具有更好的連續(xù)性.
(3)本文提出的并行不對(duì)稱空洞卷積模塊在CIFAR-10[3],孟加拉文(https://www.kaggle.com/c/bengaliaicv19/data)等數(shù)據(jù)集上得到了較好的分類效果,并可嵌入到任意的卷積神經(jīng)網(wǎng)絡(luò)中,提高模型的特征表達(dá)能力.
1 并行不對(duì)稱空洞卷積
本文提出了一種并行不對(duì)稱空洞卷積模塊,如圖1所示.通過(guò)不對(duì)稱卷積結(jié)構(gòu)的特殊性,使得模塊在不改變感受野的情況下充分利用特征圖所含信息,提高了網(wǎng)絡(luò)模型的特征表達(dá)能力.新模塊可以用來(lái)代替?zhèn)鹘y(tǒng)的連續(xù)卷積,在不增加模型復(fù)雜度的情況下,提升整個(gè)模型的準(zhǔn)確率.
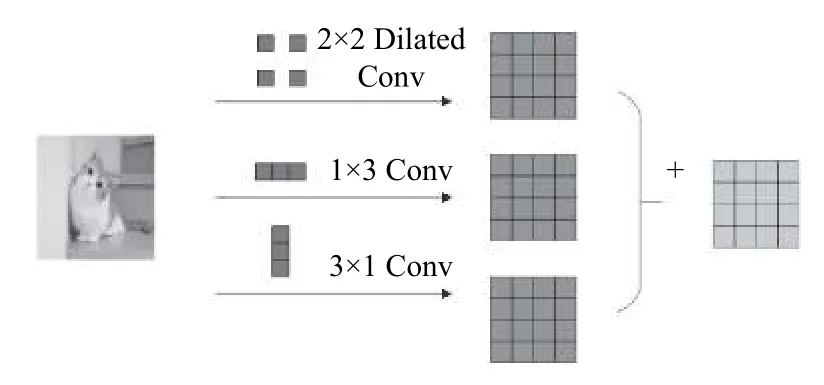
圖1 并行不對(duì)稱空洞卷積模塊
本文所提出模塊的網(wǎng)絡(luò)結(jié)構(gòu)如表1所示.

表1 并行不對(duì)稱空洞卷積模型結(jié)構(gòu)
1.1 空洞卷積的感受野
本文將從卷積操作出發(fā),在普通卷積上注入空洞,連續(xù)卷積核進(jìn)行卷積操作如式(1)[9]:
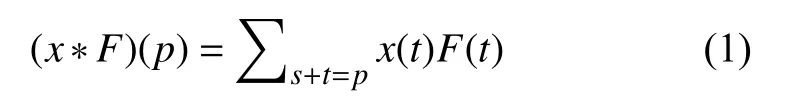
其中,*是二維卷積操作,對(duì)于輸入x∈?C×H×W,n*n卷積核f∈?C×K×H,輸出n維特征圖.對(duì)于該層的第j個(gè)卷積核,相應(yīng)的輸出特征映射通道如式(2):
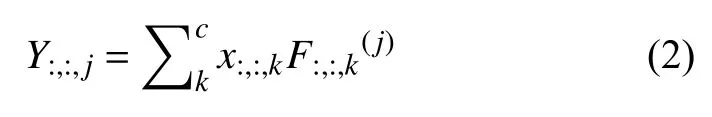
其中,χ:,:,k是x的第k個(gè)通道的特征圖,而代表的第k個(gè)尺寸為H*W卷積核.設(shè)F是一個(gè)離散過(guò)濾器即空洞卷積,定義l為空洞率,*l為空洞卷積操作:

空洞卷積支持指數(shù)擴(kuò)展的感受野,不會(huì)丟失分辨率或覆蓋范圍.將偶數(shù)尺寸的卷積核[14]通過(guò)注入奇數(shù)個(gè)空洞,其感受野范圍等價(jià)于一個(gè)奇數(shù)尺寸的連續(xù)卷積,其對(duì)應(yīng)的輸出映射通道等價(jià)于式(2),因此空洞卷積能夠代替連續(xù)卷積操作.
1.2 卷積并行性
對(duì)于經(jīng)過(guò)普通卷積后再池化的操作而言,空洞卷積不僅能夠達(dá)到與其一致的效果,而且減少了因池化所丟失的信息.與此同時(shí),空洞卷積也帶來(lái)了一些弊端.空洞卷積操作會(huì)使一些信息因特征空間上的連續(xù)而丟失,如圖像角落和邊界的信息.注入過(guò)多的空洞數(shù)量可能會(huì)導(dǎo)致預(yù)測(cè)結(jié)果出現(xiàn)棋盤效應(yīng).如果可以補(bǔ)充所丟失的連續(xù)信息,則空洞卷積可以比普通卷積提取到更有效的特征.
將幾個(gè)大小兼容的二維卷積核在相同的輸入數(shù)據(jù)上進(jìn)行相同步幅的卷積操作,可以得到相同分辨率的輸出[15].通過(guò)將這些輸出求和并在相應(yīng)的位置上進(jìn)行相加,可以得到等效核的輸出特征圖.即使卷積核大小不同,二維卷積的可加性依舊成立.因此可以引入兩個(gè)不同類型的不對(duì)稱卷積來(lái)補(bǔ)充所丟失的信息[15].
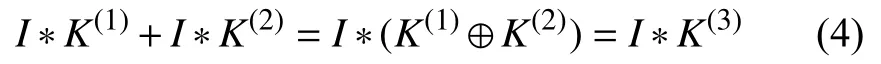
其中,I是一個(gè)輸入圖片,K(1)與K(2)是兩個(gè)相兼容的卷積核,將它們的輸出相加,操作上等價(jià)于卷積核K(3)的輸出.卷積核K(3)能 夠同時(shí)兼容K(1)與K(2).兼容是指尺寸較小的卷積核可以填充到較大的卷積核里.
如圖2所示,1*3 卷積核、3*1 卷積核和2*2 空洞卷積核因?yàn)樾螤畹募嫒菪?可以被3*3的卷積核填充.將1*3 卷積核、3*1 卷積核和2*2 空洞卷積核所形成的特征圖依次相加,其得到的特征圖和3*3 卷積核所形成的特征圖等價(jià).

圖2 卷積并行性
1.3 不對(duì)稱卷積的補(bǔ)充作用
對(duì)于對(duì)稱卷積而言,不對(duì)稱卷積更加注重特定維度的特征,其感受野與對(duì)稱卷積的感受野不同.例如1*3 卷積核在卷積的過(guò)程中,更加傾向于列間特征的提取.
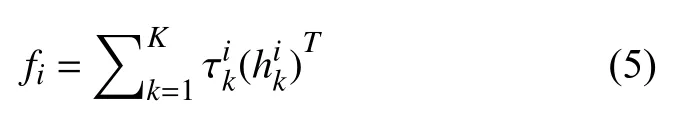
其中,fi表示n*n大小的第i個(gè) 卷積核,τ和h是兩個(gè)列向量,k是f的秩.因?yàn)榫矸e核的尺寸不同,不對(duì)稱卷積的特征提取操作與普通卷積的特征提取相比,不僅減少了對(duì)稱卷積帶來(lái)的信息冗余,而且在不對(duì)稱卷積之間又引入了非線性激活函數(shù).因此,不對(duì)稱卷積的非線性提高了網(wǎng)絡(luò)模型的擬合能力.將互相兼容的不對(duì)稱卷積得到的特征圖相加,也可以增強(qiáng)特征圖的特征表達(dá)能力.
1.4 計(jì)算量
3 *3 卷積核的感受野為9,計(jì)算量為9 *N*H*W*C,其中N是參數(shù)量,H,W分別為輸入特征圖的長(zhǎng)寬,C是輸出通道大小;卷積核尺寸為2*2,空洞率為2的空洞卷積與卷積核尺寸為3*3的卷積相比,計(jì)算量為4*N*H*W*C,在感受野相同的情況下,計(jì)算量減少了一半.與3*3 卷積相比,1*3 卷積、3*1 卷積和2*2空洞卷積三者的計(jì)算量總和僅有少量的參數(shù)增長(zhǎng).
2 實(shí)驗(yàn)及分析
2.1 實(shí)驗(yàn)設(shè)置
本文采用CIFAR-10 與孟加拉文數(shù)據(jù)集對(duì)所提出模塊的性能進(jìn)行驗(yàn)證.CIFAR-10 數(shù)據(jù)集共有60 000 張彩色圖像,這些圖像大小為32×32,分為10 個(gè)類,每類6000 張圖.孟加拉文數(shù)據(jù)集為Kaggle2020 比賽提供的數(shù)據(jù)集,包括10 000 張孟加拉文手寫體圖片.
將本文所提出的并行不對(duì)稱空洞卷積模塊嵌入到不同的基礎(chǔ)網(wǎng)絡(luò),如VGG19、ResNet-34、ResNet-50、SENet-34和SENet-50 網(wǎng)絡(luò),并與原基礎(chǔ)網(wǎng)絡(luò)進(jìn)行對(duì)比.本文使用十折交叉驗(yàn)證方法,損失函數(shù)為交叉熵?fù)p失函數(shù),學(xué)習(xí)率初始化為0.001,batchsize為128,epoch為100,均在TITAN V 上進(jìn)行試驗(yàn).
2.2 實(shí)驗(yàn)結(jié)果分析
(1)與基礎(chǔ)網(wǎng)絡(luò)進(jìn)行比較
我們采用CIFAR-10 與孟加拉文數(shù)據(jù)集,比較了VGG19、ResNet-34、ResNet-50、SENet-34、SENet-50 五種經(jīng)典的基礎(chǔ)網(wǎng)絡(luò)及其嵌入了本文所提出的并行不對(duì)稱空洞卷積模塊后網(wǎng)絡(luò)的分類效果.在嵌入模塊的網(wǎng)絡(luò)中,均將模塊嵌入到網(wǎng)絡(luò)輸出層位置,將連續(xù)卷積核和不對(duì)稱空洞卷積模塊的感受野面積都固定為9.卷積核大小為2*2,空洞率為1的空洞卷積在不對(duì)稱卷積的信息補(bǔ)充下,其準(zhǔn)確率與原基礎(chǔ)網(wǎng)絡(luò)相比有所提高.實(shí)驗(yàn)結(jié)果如表2、表3及圖3、圖4所示.通過(guò)對(duì)比可見,嵌入模塊后網(wǎng)絡(luò)的準(zhǔn)確率均有比較明顯的提升.實(shí)驗(yàn)結(jié)果表明,通過(guò)空洞卷積和不對(duì)稱卷積對(duì)特征圖的信息補(bǔ)償,使得網(wǎng)絡(luò)中所嵌入的并行不對(duì)稱空洞卷積模塊可以更好地提取特征,提高了模型的特征表達(dá)能力,提升了網(wǎng)絡(luò)的分類效果.
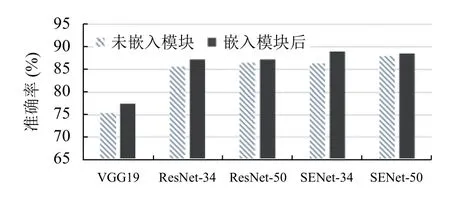
圖3 在CIFAR-10 數(shù)據(jù)集上的準(zhǔn)確率比較

圖4 在孟加拉文數(shù)據(jù)集上的準(zhǔn)確率比較

表2 在CIFAR-10 數(shù)據(jù)集上的分類準(zhǔn)確率比較(%)

表3 在孟加拉文數(shù)據(jù)集的準(zhǔn)確率比較(%)
(2)與ACNet 卷積比較
在該部分中,我們將并行不對(duì)稱空洞卷積模塊中的2*2 空洞卷積替換成3*3的普通連續(xù)卷積后,則模塊變成ACNet的不對(duì)稱卷積模塊ACB[15].我們將并行不對(duì)稱空洞卷積模塊與替換成普通連續(xù)卷積的ACB模塊分別嵌入到VGG19、ResNet-34、SENet-34 網(wǎng)絡(luò)的輸出層位置,保持相同的網(wǎng)絡(luò)結(jié)構(gòu),對(duì)CIFAR-10 數(shù)據(jù)集上的分類效果進(jìn)行比較,實(shí)驗(yàn)結(jié)果如表4及圖5所示.實(shí)驗(yàn)結(jié)果表明,嵌入并行不對(duì)稱空洞卷積模塊的網(wǎng)絡(luò)比嵌入ACB 模塊的網(wǎng)絡(luò)準(zhǔn)確率更高,模型復(fù)雜度也更低.這是因?yàn)椴粚?duì)稱卷積結(jié)構(gòu)的特殊性,使其與空洞卷積的結(jié)構(gòu)相匹配,與連續(xù)卷積搭配相比,準(zhǔn)確率要高;由于空洞卷積比連續(xù)卷積的參數(shù)要少,使得模型的復(fù)雜度也降低了很多.只有與空洞卷積相結(jié)合,不對(duì)稱卷積的特征補(bǔ)償能力才能更好地體現(xiàn).

表4 與ACB 模塊的準(zhǔn)確率及網(wǎng)絡(luò)復(fù)雜度比較

圖5 與普通卷積模塊的準(zhǔn)確率比較
2.3 損失特性分析
該部分將并行不對(duì)稱空洞卷積模塊分別嵌入到ResNet-34 網(wǎng)絡(luò)中的不同層并進(jìn)行比較,其中損失函數(shù)的振蕩變化及收斂情況如圖6所示.
當(dāng)模塊嵌入到ResNet-34 模型輸出層位置時(shí),損失函數(shù)的收斂趨勢(shì)如圖6(a)所示.當(dāng)模塊嵌入到ResNet-34 模型網(wǎng)絡(luò)輸入層位置時(shí),損失函數(shù)的收斂趨勢(shì)如圖6(b)所示.兩者的迭代次數(shù)和運(yùn)行環(huán)境均一致.可見,模塊嵌入到模型的網(wǎng)絡(luò)輸出層位置時(shí),其損失函數(shù)的振蕩比模塊嵌入到網(wǎng)絡(luò)輸入層時(shí)的振蕩要小.這是因?yàn)樵撃K中含有不對(duì)稱卷積,當(dāng)放在與輸入層比較近的位置時(shí),會(huì)導(dǎo)致網(wǎng)絡(luò)的信息損失變大,收斂速度變慢.而將模塊嵌入到網(wǎng)絡(luò)輸出層,則會(huì)加速收斂的過(guò)程,提升網(wǎng)絡(luò)的性能.

圖6 模塊嵌入到模型不同位置時(shí)模型損失函數(shù)的收斂趨勢(shì)
3 結(jié)論
本文提出了一種并行不對(duì)稱空洞卷積模塊,用不對(duì)稱卷積補(bǔ)充空洞卷積,通過(guò)不對(duì)稱卷積結(jié)構(gòu)的特殊性,在不同維度上收集特征,使得模塊在不改變感受野的情況下充分利用特征圖的信息,提高了網(wǎng)絡(luò)模型的特征表達(dá)能力.同時(shí),該模塊通過(guò)引入空洞卷積,使得模型在與普通卷積復(fù)雜度相近的情況下,達(dá)到使用同樣感受野尺寸的普通卷積的分類效果.不對(duì)稱卷積補(bǔ)充了空洞卷積所丟失的信息,補(bǔ)充了不同維度的信息,而且加速了整個(gè)網(wǎng)絡(luò)的收斂過(guò)程,提高了網(wǎng)絡(luò)的效率.本文將該模塊嵌入到五種基本網(wǎng)絡(luò),并對(duì)CIFAR-10 與孟加拉文數(shù)據(jù)集進(jìn)行了分類比較,結(jié)果準(zhǔn)確率均有較大的提高.該模塊可嵌入其它任何網(wǎng)絡(luò)模型中,幫助提高網(wǎng)絡(luò)模型的分類效果,也可遷移到其它圖像的分類任務(wù)當(dāng)中.

