表貼式多相分數槽繞組電機的電感分析?

戴雅婷 李東臻 邱 原

（海軍工程大學 武漢 430033）

1 引言

無刷直流電機由于結構和驅動控制方法簡單，控制方式類似于傳統的直流電機，因此在中小功率傳動場合得到了廣泛的應用［1］。大容量傳動場合可采用多相分數槽繞組降低每相容量，同時提高轉矩密度和減小電流諧波［2］。合適的電機極、槽數的分數槽繞組，還能夠有效地抑制無刷直流電機的轉矩脈動［3］。

電機電感參數對于建立電機數學模型、分析電機性能與研究控制策略十分重要。多相分數槽繞組電機不能沿用傳統三相整數槽電機的傳統電感計算方法，這是由于［4～8］：

1）不同于正弦波供電的交流電機，電機的方波氣隙磁密均參與產生有效電磁轉矩，因此相繞組磁通的各次諧波應計入主電感，而不是單獨計算諧波漏感；

2）相繞組通入的電流為近似方波，不同于交流電機的正弦波；

3）電機若采用表貼式磁極，等效氣隙大，主電感與漏電感較接近；

4）各相繞組的互感不按空間位置角的余弦規律變化，需按照各相的繞組函數重新推導，而分數槽繞組的相互關系更加復雜。

一般來說，電感的計算可以分為由基本元件磁勢分析出發的磁路方法［9～10］、采用等效面電流的解析磁場方法［11～12］或有限元法。有限元計算方法精度高，能夠考慮鐵芯的飽和，但計算時間長、物理意義也不明確，難以獲得自感與各相互感的關系。解析磁場方法雖有明確的物理意義，但推導十分復雜。因此本文從解析磁路出發，借鑒繞組函數的思路，推導多相分數槽繞組無刷直流電機的通用電感計算公式。

2 電感計算的基本方法

分析對象為表貼式永磁電機，并作如下假設。

1）假設鐵芯材料的磁導率為無窮大，忽略鐵芯材料的飽和與損耗；

2）沿圓周方向氣隙均勻，各處磁導相同，永磁體的氣隙處磁密波形為理想方波；

3）氣隙磁場的正方向規定為由轉子外表面進入定子為內表面。

由電感L的含義可知，其為磁鏈ψ與產生該磁鏈的電流i之比為

磁鏈是磁通Φ與所交鏈線圈匝數N的乘積，即：

根據磁路歐姆定律，磁通可由磁動勢（MMF）與磁路磁導的乘積求得

因此電感計算的關鍵在于求得該電流在磁路上所產生的磁動勢F與磁路處的磁導λ。對于電機繞組的電感計算，由于假設中忽略了鐵芯材料的磁壓降，因此主要問題在于計算沿氣隙圓周的磁動勢及氣隙處磁導。

氣隙磁動勢的計算可借鑒繞組函數的思想，不用考慮整數槽繞組與分數槽繞組的區別，由安培環路定理得到其分布函數，從而得到通用的電感計算公式。

3 電樞反應自感的計算

首先計算一相繞組通入電流im后在氣隙產生的磁動勢。

分數槽結構的相繞組由分布于多個單元電機、同相位的線圈組成，考慮到單元電機之間完全對稱的繞組分布，氣隙磁動勢的分布完全一致，于是可以將單元電機作為對象分析相繞組產生的磁動勢。

在單元電機內，一個節距為y（按槽數計算）、匝數為Nc的線圈嵌放在定子槽內（見圖1）。

圖1 繞組元件在氣隙中產生的磁動勢

當線圈通入電流ic時，它將在在氣隙圓周上產生一個閉合磁場，考慮到正方向的規定，該定子磁動勢沿氣隙圓周將按圖示分布。由磁路的安培環路定理可知，線圈所產生的磁動勢為磁力線所包圍的總電流，它的幅值就為

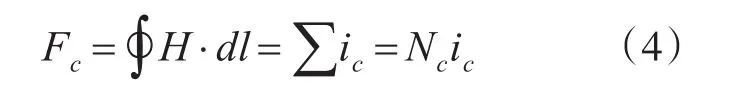
由磁通連續性定理，該線圈磁動勢所產生的磁通進入定子軛部與從定子軛部穿出的磁通量必然相等，但由于線圈的跨距不是半個單元電機圓周，因此兩個方向磁通通路的面積不同，磁動勢沿氣隙圓周的分布必然也不同，它與通路面積成反比。由于給位置鐵芯軸向長度一致，通路面積與各自磁路的圓周長度決定。以繞組槽數為單位計算，定義x為沿圓周方向的槽數，原點位于線圈的軸線。由以上分析知道沿圓周的氣隙磁動勢的表達式為

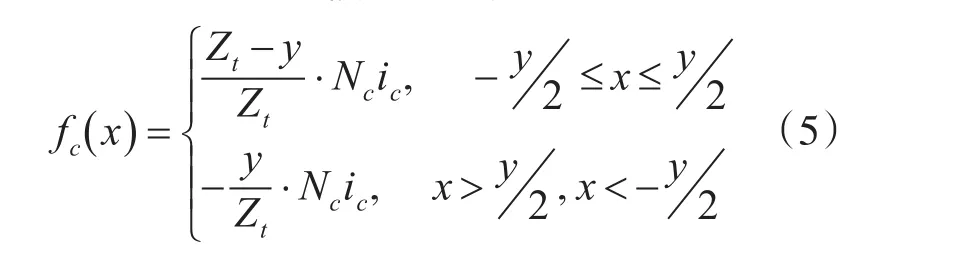
式中Zt為單元電機的槽數。在得到單個線圈在氣隙產生的磁動勢后下一步需要計算氣隙處磁通路徑的磁導，氣隙磁導計算式為

式中δef是考慮了永磁體厚度的等效氣隙長度，Ag是與繞組交鏈的氣隙磁通路徑面積，其表達式分別為

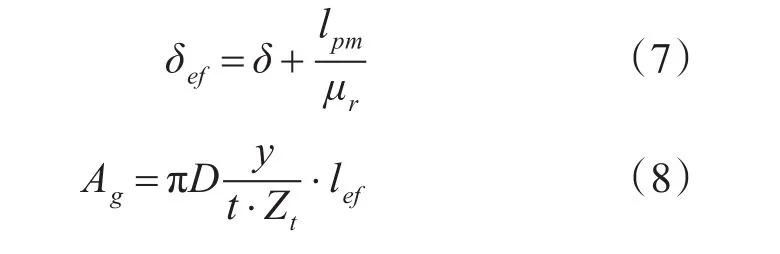
式中δ為氣隙長度；lpm為永磁體厚度；μr為永磁體的相對磁導率；t為單元電機數；D為氣隙圓周處的直徑；lef為定子鐵芯的有效長度。

在得到沿氣隙分布的磁動勢表達式與氣隙磁導后，在線圈跨距y個槽內累加得到與線圈交鏈的磁通，為

4 電樞反應互感的計算

對于多相繞組結構，根據兩相繞組的相互位置，它們的互感計算需要分為三種情況。下面計算第k相對第j相繞組的互感。兩相繞組相距的槽數為|k-j|。

4.1 | k-j|＜y的情況

|k-j|＜y時兩相繞組位置的相互關系如圖2，k相線圈在氣隙中產生的磁通與j相線圈交鏈的部分既有正向，又有反向。

圖2 |k-j|＜y時兩線圈相互位置

此時k相線圈在氣隙中產生的磁動勢分為

下面需要分別計算磁通正向部分與反向部分的氣隙處磁導，它們的區別僅在于磁通路徑沿圓周方向的長度不同，分別為

按照與自感相同的計算方法可以得到兩部分的氣隙磁導，λ+和λ-。在線圈跨距y個槽內累加，得到k相線圈在氣隙中產生的磁通與j相線圈交鏈的部分之和。

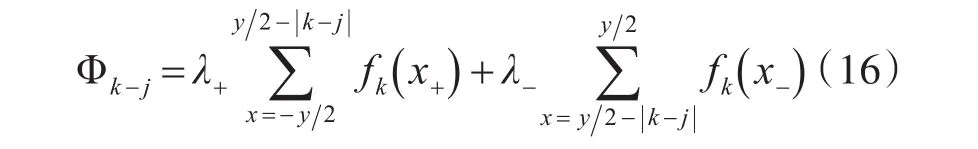
4.2 y≤| k-j|≤z-y的情況

y≤| k-j|≤z-y時兩相繞組位置的相互關系如圖3，此時k相線圈在氣隙中產生的磁通與j相線圈交鏈的部分全為反向。

圖3 y≤| k-j|≤z-y時兩線圈相互位置

4.3 | k-j|＞z-y的情況

|k-j|＞z-y時兩相繞組位置的相互關系如圖4所示，k相線圈在氣隙中產生的磁通與j相線圈交鏈的部分同樣既有正向，又有反向。

圖4 | k-j|＞z-y時兩線圈相互位置

此時k相線圈在氣隙中產生的磁動勢分別為

下面需要分別計算磁通正向部分與反向部分的氣隙處磁導，它們的區別僅在于磁通路徑沿圓周方向的長度不同，分別為按照與自感相同的計算方法可以得到兩部分的氣隙磁導，λ+和λ-。在線圈跨距y個槽內累加，得到k相線圈在氣隙中產生的磁通與j相線圈交鏈的部分之和。

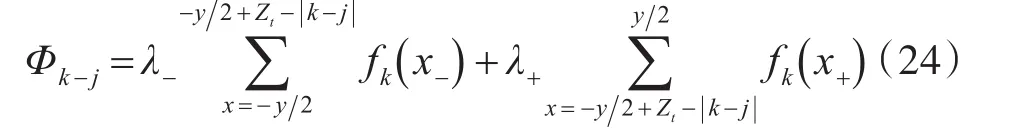
在線圈跨距y個槽內累加，得到k相線圈在氣隙中產生的磁通與j相線圈交鏈的部分之和。

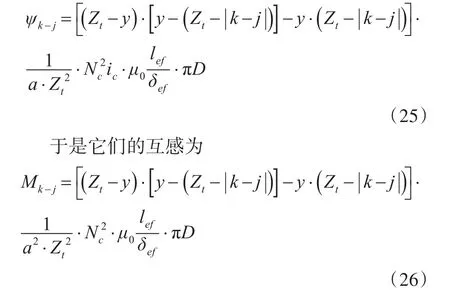
將式（18）、（21）、（26）三式統一起來便得到兩相繞組的互感完整表達式。

5 漏電感與總電感的計算

電機漏電感是由不穿過氣隙的磁通引起的，由于分數槽繞組特別是節距y較小時的電機端部繞組很短，端部漏電感含量較小，因此電機漏電感的主要成分是槽漏電感。槽漏電感的計算方法與傳統交流電流類似，這里不再贅述。

需要注意的是，槽漏感既存在與一相繞組的自感中，也存在滿足一定關系的兩相繞組互感中，如圖5所示。一相繞組的槽漏電感是相繞組線圈的原邊與副邊元件經槽底、槽內空間、槽口閉合的漏磁場分量，定義為Lls；當兩相繞組相距的槽數恰好等于相繞組的跨距時，它們有元件邊同槽，磁鏈會通過定子齒槽相互交鏈，于是兩相繞組有互感作用，定義為Llm。

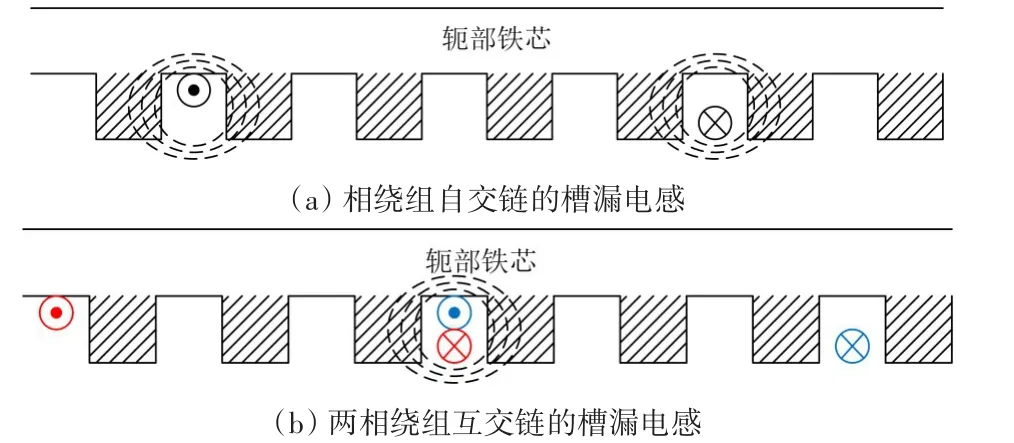
圖5 槽漏電感的磁路

6 算例

以一臺8極、46槽、23相無刷直流電機為例，通過有限元仿真驗證電機電感參數的計算結果。該電機由兩個4極23槽單元電機組成，兩單元電機間的線圈串聯成一相繞組，電機的具體參數如表1所示。

表1 算例參數

由電機的結構參數代入上文推導的電感計算表達式，能夠計算電樞得到相繞組的主自感Lm，一相的槽漏電感Lls，兩相互交鏈的槽漏電感Llm及各相間的互感Mtotal_k-j。解析計算公式的一項優勢是能夠得到電機各電感參數間的關系，例如當|k-j|<6時，各相間的互感為

利用ANSYS Maxwell 16.0建立如圖6的電機有限元仿真模型驗證電感的計算結果，有限元仿真采用靜態求解器。

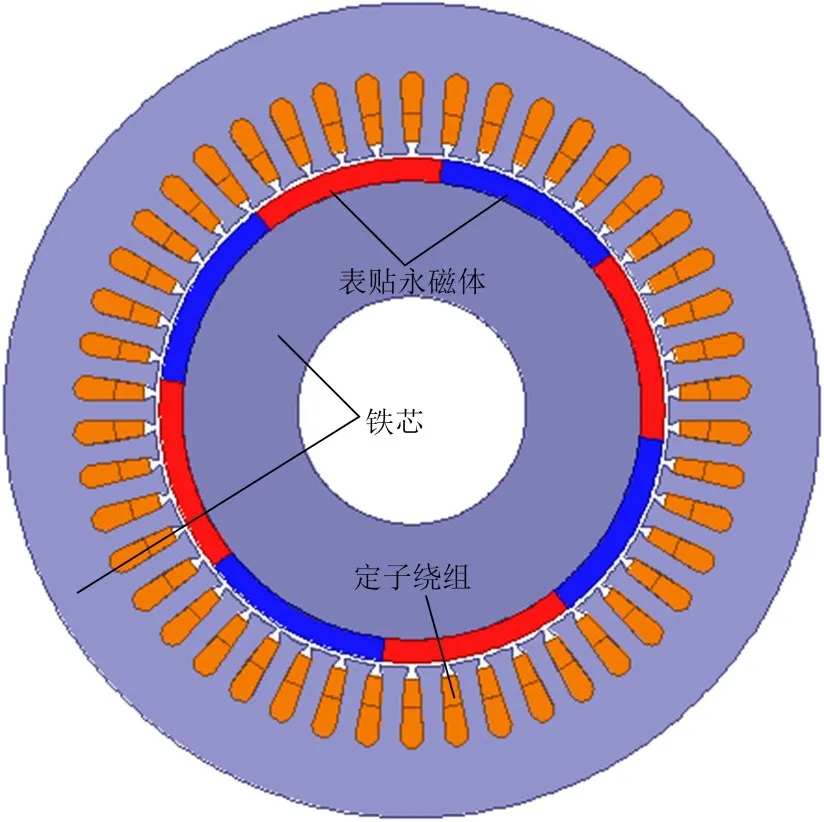
圖6 電感計算的有限元模型

解析方法與有限元仿真的部分結果如表2，由于互感矩陣具有對稱性，因此所給出的結果已經能夠驗證計算結果。電感計算的誤差在7%以內，滿足工程需求，若考慮定子開齒及飽和的影響，計算精度將進一步提高。這種計算方法最大的好處是能夠獲得電機各自感之間的關系，從而非常方便編程計算多相電機中數目眾多的電感參數。

表2 電感計算結果

7 結語

本文針對表貼式多相分數槽繞組無刷直流電機，借鑒繞組函數的思路，由磁路方法解析推導了通用的電感計算公式，其計算過程簡單，物理意義清晰，并通過有限元仿真驗證了計算結果，驗證結果表明滿足工程精度需求。該解析公式能夠得到電機自感與各相互感間的關系，因此能夠大大減少多相繞組電感參數的數目，有利于編程計算和多相電機數學模型的建立。

本文所推導的通用計算公式適用于不同結構的分數槽繞組，例如當y=1時可以計算集中繞組結構的電感。由于整數槽結構屬于分數槽繞組的一種特殊情況，因此同樣可以用來計算多相整數槽結構的各相電感。