OFDM調制解調系統設計與仿真

薛鳳鳳，曹帥，葉立庭，田琴

（空軍工程大學信息與導航學院，陜西西安，710082）

0 引言

隨著通信技術的不斷發展，可靠、快速、高效逐步成為人們對通信追求的主潮流。為適應人們的通信需求，作為一種特殊的多載波調制技術，正交頻分復用（OFDM）技術越來越受到工程技術人員的關注。OFDM技術從二十世紀六十年代被提及至今，已有六十多年發展的歷史，由于它具有高頻譜效率、抗干擾能力強、適宜寬帶傳輸等特點，被數字電視、無線局域網、移動通信等通信系統采用，成為寬帶數字通信的基礎調制方式之一[1]。

OFDM技術發源于多載波傳輸技術。相比于其它傳輸技術，OFDM技術能夠在頻域上實現并行復用，對相同信息量實現高速率傳輸，達到高效利用頻譜資源的目的。另外，OFDM技術通過添加保護間隔、插入導頻等手段實現收發同步、優化信道估計算法，能夠有效抵抗多徑時延引起的碼間干擾。基于此等優勢，OFDM技術在未來無線通信技術的發展中仍然占據著核心地位，以其抗多徑能力強、頻譜利用率高、易于實現的優勢對移動通信具有廣闊的應用價值。本文通過對OFDM技術進行研究介紹、設計仿真，驗證該技術系統的性能優勢。

1 OFDM基本原理

對于一個OFDM符號來說，自身包含一定數量的子載波，不是單一信號，具備合成信號的特征。可以說，任何子載波都可能受到相關調制裝置的調制。下列公式(1)展示了子載波調制的基本算法，其中N表示的是子信道的個數，T為OFDM符號的寬度，是分配給每個子信道的數據符號，f0是第零個子載波的載波頻率，矩形脈沖，則從t=ts開始的OFDM符號可以表示為：

對于OFDM信號，在其連續信號的數學模型中，N個頻率上的多載波調制信號為

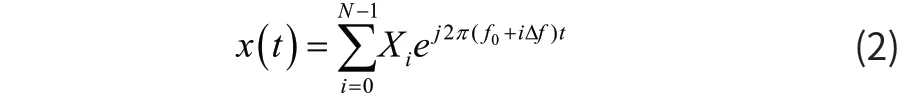
上式中，0f為初始頻率，fΔ 為頻率的間隔大小，iX是調制頻率if上的復數符號[2]。

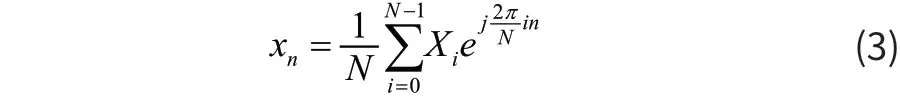
上式即為OFDM調制信號的基本運算公式。將其同離散傅里葉逆變換公式相比較可以發現，兩個表達式是相一致的，因此，為形成特定的OFDM信號，可以合理運用IDFT/DFT變換公式。結合公式屬性，使用快速變換傅里葉變換，能夠大幅度降低轉換的復雜性和操作的難度，進一步提升系統調制解調效率。

2 OFDM系統設計

2.1 幀結構設計

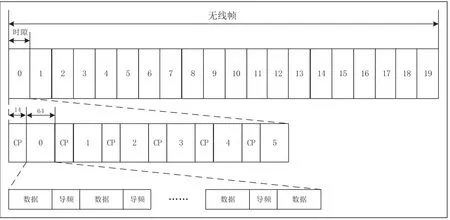
圖1 OFDM幀結構

參考LTE系統基本幀結構，在OFDM系統符號中插入導頻數據，進行OFDM幀結構設計。在該幀結構中，每個無線幀包含10個子幀，20個時隙。其中，每兩個時隙組成一個子幀，每個時隙由6個OFDM符號組成，每個OFDM符號由保護間隔CP、數據信息和導頻信息三部分組成，導頻信息在數據信號間等間隔排列。

2.2 系統參數

在實際中，各種信道因素、各項性能要求對OFDM系統參數的選取配置有著重大的影響。我們往往參考給定信道帶寬、時延長度和系統比特率三項因素，按照設計方案和項目預期，本次設計對有關參數進行合理選取。關于OFDM系統的基本參數見表1。

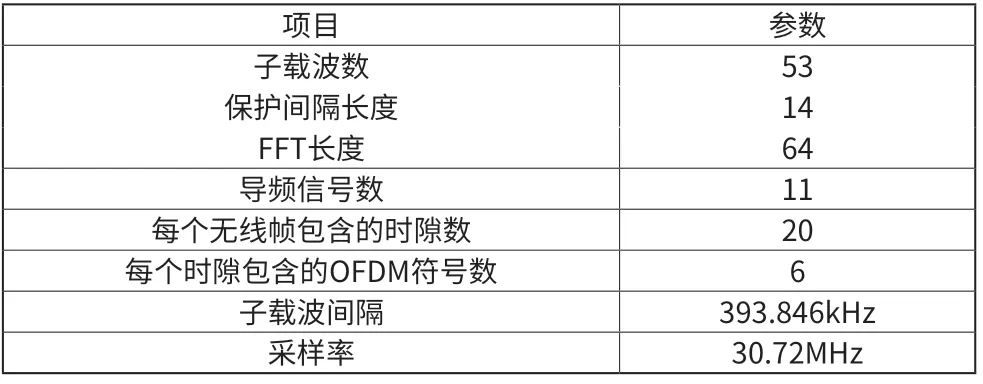
表1 系統基本參數配置

2.3 系統模型

在發送機部分，輸入的串行數據通過系統中的編碼、交織后依據信道穩定性和系統選擇進行相對應的數字調制映射，再給調制映射后的信號進行導頻插入處、串并轉換處理后，將產生的并行數據送入IFFT處理模塊，完成處理后，數據接續進行并串轉換等操作，最后向外輸出可被接收執行的調制信號。

與此相對的接收部分，完成信號接收后，會依次進行下變頻、模數變換、移除循環間隔、串并轉換一系列基帶信號處理后，送至FFT處理模塊進行信號解調運算，形成的并行數據經過并串轉換后進行信道估計、校正，以減小信道帶來的隨機性誤差。隨后，參照信號幅值大小、實際相位情況，對數字信號展開一系列的處理，使其恢復出最初的輸入數據。

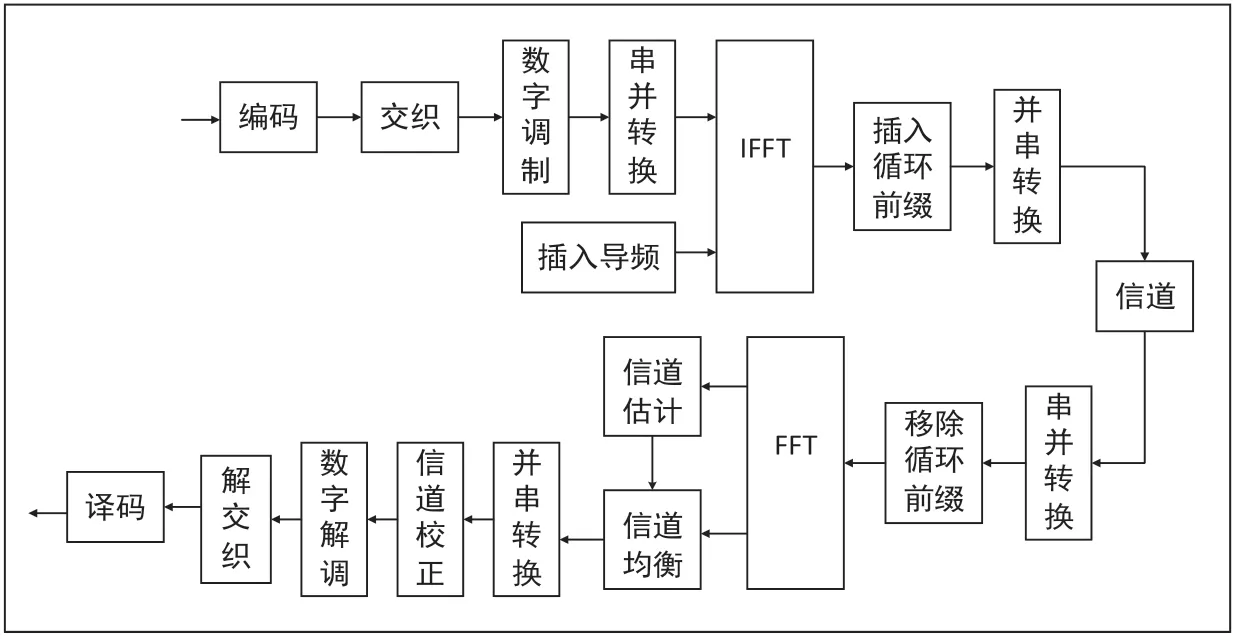
圖2 OFDM系統架構

3 系統仿真及性能分析

3.1 關鍵模塊設計

(1)信道編譯碼

OFDM系統采用信道編碼對傳輸后的信號進行振幅偏差糾錯，本次設計采用有效約束長度為7，八進制代碼表示為[133 171]的卷積編碼。相應的，采用屬于概率譯碼的Viterbi算法進行信道譯碼。結合MATLAB語言特點，運用poly2trellis()函數生成相應卷積碼，分別采用conven()函數和vitdec()函數實現信道編譯碼功能。

實現代碼為：

code_data=conv1(P_data)；

rx_c_de1=vitdec(data_jiejiaozhi,trellis,tblen,'trunc','hard');

(2)交織與解交織

交織與解交織是將OFDM系統中突發性錯誤轉換為隨機性錯誤的一種技術，可以進一步提高OFDM系統的糾錯能力。該技術主要是通過不同方式實現對數據的輸入輸出，具體表現為“按行輸入，按列輸出”。MATLAB實現代碼為：

data_jiaozhi=jiaozhi(code_data,mod_type)；

data_jiejiaozhi=jiejiaozhi(De_Bit,mod_type)；

(3)調制映射與解調制映射

本此設計中，OFDM系統采用的調制方式包括QPSK、16QAM、64QAM。MATLAB實現代碼為：

[mod_data,mod_data_real,mod_data_imag]= mmod(data_jiaozhi,mod_type)；

[output]=OFDM_de_mod( input,mod_type )；

(4)保護間隔

在OFDM系統中可添加的保護間隔類型包括循環前綴、循環后綴和零符號填充[3]。本次設計中采用插入循環前綴的方式相對于另外兩種方式效率較高，既可以抵抗多徑延遲干擾，也可以建立OFDM符號的循環重構。MATLAB實現代碼為：

TX_cd=[ifft_data(N_fft-N_cp+1:end,:)

(5)基于導頻設計的信道估計

本此設計中所采用的做法是在導頻信號的參考下進行信道估計。應用的主要原理是，借助在發射端形成的基帶信號中插入的梳狀結構導頻信號，在接收端處理獲得的導頻信號根據前者進行導頻信號位置處的信道估計，并利用線性插值獲得兩個導頻信號之間的信號傳輸函數[4]。MATLAB實現代碼為：

[data,P_f_station,pilot_seq,data_station]=add_pilot(spread_data,P_f_inter,N_fft,N_sc);

[data3,H]=guji(N_fft,fft_data,P_f_station,pilot_seq,data_station); %信道估計

3.2 系統性能分析

以QPSK調制為例，調整信噪比SNR分別為15dB和25dB時，接收端星座圖如圖3、4所示。顯然，信噪比越高，星座圖中在（±0.707，±0.707）周圍落點形成的圓越小，數據映射越準確，接收端數據恢復越準確[5]。

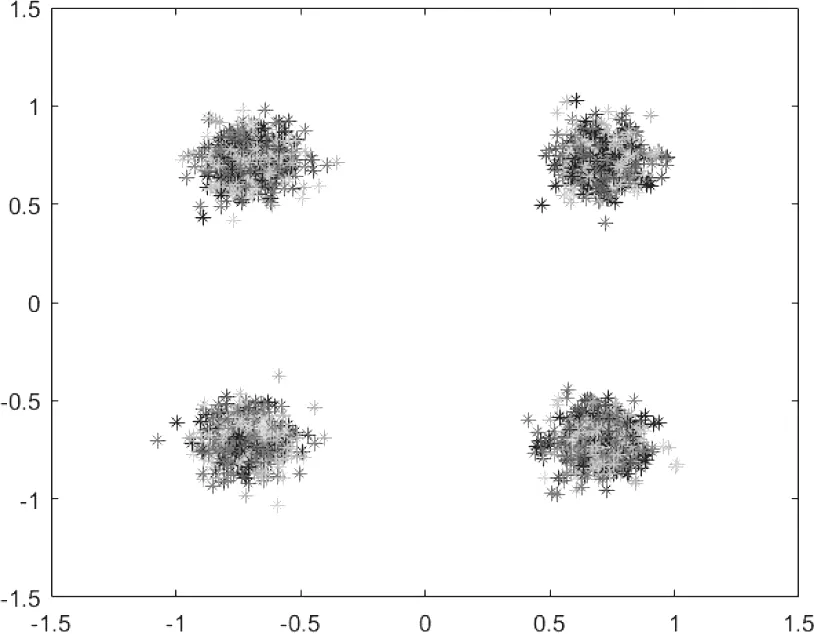
圖3 SNR為15dB時QPSK星座圖

圖4 SNR為25dB時QPSK星座圖

根據一般工程要求，將信噪比設置在0～25dB范圍內變化，系統誤碼率特性曲線如圖5所示。總體上，系統可靠性在QPSK調制方式下最佳，16QAM次之，64QAM最差。主要原因為，相同信道帶寬下，調制階數越高，對系統的信噪比要求越高[6]。

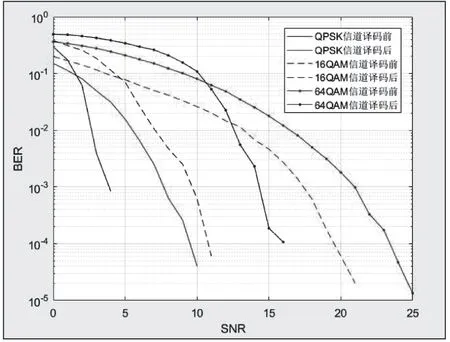
圖5 系統誤碼率特性曲線

另外，從三種調制模式下編譯碼前后誤碼率對比中可以發現，當信噪比SNR比較大時，信道編碼的優勢非常明顯，三種調制模式下的誤碼率信道編碼前的誤碼率均小于信道編碼后，并且呈快速下降趨勢。但是，當信噪比SNR比較小時，信道編譯碼前的數據誤碼率反而小于信道編碼后。這是因為信道編譯碼前的誤碼率就已經達到一個很高的數值，卷積編碼的糾錯效能失效，以致于正確的信息也被混淆在錯誤信息之中，使誤碼率升高[7]。由于在一般情況下進行傳輸信息的信噪比會比較高，編碼的糾錯效能隨之也會被最大限度地發揮出來。

4 結語

本文通過對OFDM調制解調系統進行設計，應用MATLAB實現OFDM系統中信號產生與接收、信道編譯碼、交織與解交織、調制映射與解調制映射、插入導頻與信道估計、等模塊的仿真后，建成OFDM系統展示平臺。對系統不同信噪比SNR下的星座圖和誤碼率特性曲線進行分析，進一步驗證了系統在高信噪比、低階調制下的誤碼率特性較好。