成對(duì)型復(fù)微分差分多項(xiàng)式的零點(diǎn)與唯一性

劉 凱，高迎春

(1.南昌大學(xué)數(shù)學(xué)系，江西 南昌 330031)

1 引言及主要結(jié)果

本文假設(shè)讀者熟悉亞純函數(shù)值分布理論[1-2]的基本概念和符號(hào)。例如：特征函數(shù)T(r,f),計(jì)數(shù)函數(shù)N(r,f)和均值函數(shù)m(r,f)。函數(shù)增長級(jí)ρ(f)和超級(jí)ρ2(f)定義如下：

若亞純函數(shù)a(z)滿足T(r,a(z))=o(T(r,f))=S(r,f),r→∞至多除去一個(gè)具有有限對(duì)數(shù)測(cè)度的例外集，則稱函數(shù)a(z)為f(z)的小函數(shù)。

亞純函數(shù)的零點(diǎn)研究是值分布理論的一個(gè)重要課題，代數(shù)學(xué)基本定理說明任何非零多項(xiàng)式都存在零點(diǎn)，經(jīng)典的Picard定理說明超越整函數(shù)f(z)至多有一個(gè)有限的Picard例外值，即f(z)-a有無窮多個(gè)零點(diǎn)至多有一個(gè)例外的a值；而超越亞純函數(shù)至多有兩個(gè)有限的Picard例外值。Hayman[3]研究了復(fù)微分多項(xiàng)式f(z)nf′(z)-a的零點(diǎn)個(gè)數(shù)問題，此類問題是研究復(fù)微分多項(xiàng)式零點(diǎn)的重要起點(diǎn)，后續(xù)很多亞純函數(shù)零點(diǎn)問題、唯一性問題和正規(guī)族理論的研究都受此問題的啟發(fā)。

定理A[3，定理10]設(shè)f(z)是超越整函數(shù)且n≥2為正整數(shù)，a是非零常數(shù)，則f(z)nf′(z)-a有無窮多個(gè)零點(diǎn)。

Clunie[4]證明了當(dāng)n=1時(shí)定理A也是正確的。那么，如果f(z)是超越亞純函數(shù)，情況會(huì)如何呢？Hayman在文獻(xiàn)[3]中提出如下猜想:

Hayman猜想：設(shè)f(z)是超越亞純函數(shù)且n是正整數(shù)，a是非零常數(shù)，則f(z)nf′(z)-a有無窮多個(gè)零點(diǎn)。

事實(shí)上，Hayman[3]得到了下面結(jié)果：

定理B[3]設(shè)f(z)是超越亞純函數(shù)且n≥3是正整數(shù)，a是非零常數(shù)，則f(z)nf′(z)-a有無窮多個(gè)零點(diǎn)。

在眾多數(shù)學(xué)家的努力下，Hayman猜想現(xiàn)已被完全證明，其中Mues[5]證明了定理B中n=2的情況，Bergweiler和Eremenko[6]，Chen和Fang[7]以及Zalcman[8]分別證明了n=1的情況。Hayman猜想說明對(duì)于特殊類型的亞純函數(shù)f(z)nf′(z)的Picard例外值僅可能為0。目前，與Hayman猜想有關(guān)的問題研究依然十分活躍。2007年，Laine和Yang[9，定理2]首次研究了Hayman猜想的差分版本，即復(fù)差分多項(xiàng)式的零點(diǎn)分布，并得到了下列結(jié)果：

定理C設(shè)f(z)是有窮級(jí)超越整函數(shù)且a和c是非零常數(shù)，則當(dāng)n≥2時(shí)，f(z)nf(z+c)-a有無窮多個(gè)零點(diǎn)。

之后，各種類型的復(fù)差分多項(xiàng)式的零點(diǎn)和值分布問題得到了廣泛研究，例如：Liu和Yang[10，定理1.4]研究了f(z)n[f(z+c)-f(z)]-p(z)的零點(diǎn)分布情況，其中p(z)是一個(gè)多項(xiàng)式。Luo和Lin[11，定理1]將定理C中常數(shù)a替換成了f(z)的小函數(shù)a(z)，將f(z)n替換成了f(z)的多項(xiàng)式，并得到了下面的結(jié)果：

定理D設(shè)f(z)是有窮級(jí)超越整函數(shù),c是非零常數(shù)，an(≠0),an-1,…,a0是常數(shù)，P(z)=anzn+an-1zn-1+…+a1z+a0，且P(z)有t個(gè)判別的零點(diǎn)，如果n>t，則P(f)f(z+c)-a(z)有無窮多個(gè)零點(diǎn)，其中a(z)為f(z)的非零小函數(shù)。

如果定理C中有窮級(jí)超越整函數(shù)替換成超級(jí)小于1的超越亞純函數(shù)，Liu，Liu和Cao[12]證明n≥6時(shí)定理C成立，Wang和Ye[13]改進(jìn)到n≥4，Liu，Liu和Cao[12]構(gòu)造反例說明n≤3時(shí)定理C不成立。關(guān)于定理D的亞純情況及其他類型微分差分方面的研究可見專著Liu，Laine和Yang[14,第2章]。在上述的研究中，所有的研究思路都集中在函數(shù)及其本身的微分差分多項(xiàng)式的研究上。而構(gòu)建成對(duì)型的問題是Hayman猜想有趣的創(chuàng)新，例如：設(shè)f(z)和g(z)是超越亞純函數(shù)，a為非零常數(shù)，那么能否得到fn(z)g′(z)-a與gn(z)f′(z)-a二者之一必有無窮多個(gè)零點(diǎn)？如果能證得，那么取f=g便可以得到定理A，B的結(jié)果。基于上述的研究思路，Gao和Liu[15]首次研究了成對(duì)型微分差分多項(xiàng)式f(z)nL(g)-a(z)和g(z)nL(f)-a(z)的零點(diǎn)分布情況，其中a(z)是f(z)和g(z)的非零小函數(shù)，L(h)可以取高階導(dǎo)數(shù)h(k)(z)，平移h(z+c)，差分h(z+c)-h(z)和延滯微分h(k)(z+c)四種情況。為表述簡潔，我們用M表示超越亞純函數(shù)類，M′表示超級(jí)小于1的超越亞純函數(shù)類，E表示超越整函數(shù)類，E′表示超級(jí)小于1的超越整函數(shù)類。

Gao和Liu[15]得到了下面的定理：

定理E設(shè)f(z)和g(z)是超越亞純函數(shù)，若滿足下面的任意一個(gè)條件：

ⅰ.當(dāng)L(h)=h(k)(z)，若h∈M且n≥k+4或者h(yuǎn)∈E且n≥3；

ⅱ.當(dāng)L(h)=h(z+c)，若h∈M′且n≥4或者h(yuǎn)∈E′且n≥3；

ⅲ.當(dāng)L(h)=h(z+c)-h(z)，若h∈M′且n≥5或者h(yuǎn)∈E′且n≥3；

ⅳ.當(dāng)L(h)=h(k)(z+c)，若h∈M′且n≥k+4或者h(yuǎn)∈E′且n≥3，

則f(z)nL(g)-a(z)和g(z)nL(f)-a(z)至少一個(gè)有無窮多個(gè)零點(diǎn)，a(z)是f(z)和g(z)的非零小函數(shù)。

文[15]中，Gao和Liu進(jìn)一步考慮了相應(yīng)的分擔(dān)公共值的唯一性問題，得到了下面的定理：

定理F設(shè)f(z)和g(z)是超越亞純函數(shù)，a(z)是f(z)nL(g)和g(z)nL(f)的CM公共小函數(shù)，其中a(z)是f(z)和g(z)的非零小函數(shù)。如果下面的任意一個(gè)條件滿足：

ⅰ.當(dāng)L(h)=h(k)(z)，若f，g∈M且n≥3k+16或f，g∈E且n≥8；

ⅱ.當(dāng)L(h)=h(z+c)，若f，g∈M′且n≥16或f，g∈E′且n≥8；

ⅲ.當(dāng)L(h)=h(z+c)-h(z)，若f，g∈M′且n≥19或f，g∈E′且n≥8；

ⅳ.當(dāng)L(h)=h(k)(z+c)，若f，g∈M′且n≥3k+16或f，g∈E′且n≥8

則有f(z)nL(g)=g(z)nL(f)或者f(z)nL(g)g(z)nL(f)=a(z)2。

注當(dāng)L(h)取特殊情況時(shí)，可以得到f和g的關(guān)系，可見[15]。

本文將考慮具一般形式成對(duì)型微分差分多項(xiàng)式P(f)L(g)-a(z)和P(g)L(f)-a(z)的零點(diǎn)情況，其中P(z)為n次多項(xiàng)式有t個(gè)判別零點(diǎn)，且有t1個(gè)單零點(diǎn)和t2個(gè)重零點(diǎn)(t1+t2=t)，記Γ0=t1+2t2。設(shè)P(z)=a(z-z1)s1(z-z2)s2…(z-zt)st(s1+s2+…+st=n)。考慮以下三種不同的L(h)的情況：

D(h)=akh(k)(z)+ak-1h(k-1)(z)+…+a1h′(z)+a0h(z)(k≥1)

(1.1)

Q(z,h)=amh(z+cm)+am-1h(z+cm-1)+…+a1h(z+c1)+a0h(z+c0)

(1.2)

D(z,h)=amh(km)(z+cm)+…+a1h(k1)(z+c1)+a0h(k0)(z+c0)

(1.3)

這里c0,…,cm為互相判別的復(fù)數(shù)且ai為常數(shù)。記kM=km+km-1+…+k0+m+1。

定理1.1假設(shè)P(z)如上定義且下列條件之一滿足：

1.L(h)=D(h(z))，若h∈M且n≥t+k+3或者h(yuǎn)∈E且n≥t+2；

2.L(h)=Q(z,h)，若h∈M′且n≥t+m+3或者h(yuǎn)∈E′且n≥t+2；

3.L(h)=D(z,h)，若h∈M′且n≥t+kM+2或者h(yuǎn)∈E′且n≥t+2；

則P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一個(gè)有無窮多個(gè)零點(diǎn)，a(z)是關(guān)于f(z)和g(z)的非零小函數(shù)。

定理1.2設(shè)f(z)和g(z)是超越亞純函數(shù)，若a(z)是P(f)L(g)和P(g)L(f)的CM公共小函數(shù)，其中a(z)是f(z)和g(z)的非零小函數(shù)，且下面的任意一個(gè)條件滿足:

1.當(dāng)L(h)=D(h(z))，若f，g∈M且n≥2Γ0+3k+12；

2.當(dāng)L(h)=Q(z,h)，若f，g∈M′且n≥2Γ0+3m+6；

3.當(dāng)L(h)=D(z,h)，若f，g∈M′且n≥2Γ0+3kM+4m+5，

則P(f)L(g)=P(g)L(f)或者P(f)L(g)P(g)

L(f)=a(z)2。

如果考慮f(z)和g(z)是超越整函數(shù)，利用類似定理1.2的證明方法，可以得到

定理1.3設(shè)f(z)和g(z)是超越整函數(shù)，若a(z)是P(f)L(g)和P(g)L(f)的CM公共小函數(shù)，其中a(z)是f(z)和g(z)的非零小函數(shù)，且下面的任意一個(gè)條件滿足：

ⅰ.當(dāng)L(h)=D(h(z))，若f，g∈E且n≥2Γ0+4；

ⅱ.當(dāng)L(h)=Q(z,h)，若f，g∈E′且n≥2Γ0+4；

ⅲ.當(dāng)L(h)=D(z,h)，若f，g∈E′且n≥2Γ0+4；

則有P(f)L(g)=P(g)L(f)或者P(f)L(g)P(g)L(f)=a(z)2。

2 引理

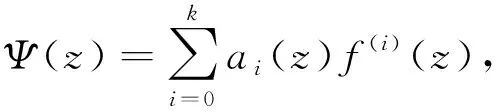
這里ai(z)(i=0,1,…,k)均為f(z)的小函數(shù)，則

(2.1)

T(r,Ψ)≤(k+1)T(r,f)+S(r,f)

(2.2)

引理2.2[16]設(shè)f(z)為超級(jí)小于1的超越亞純函數(shù)，則

T(r,f(z+c))=T(r,f)+S(r,f),N(r,f(z+c))=N(r,f)+S(r,f)

(2.3)

(2.4)

引理2.3若L(h)分別取(1.1)(1.2)和(1.3)，可以得到下面特征函數(shù)的估計(jì)式：

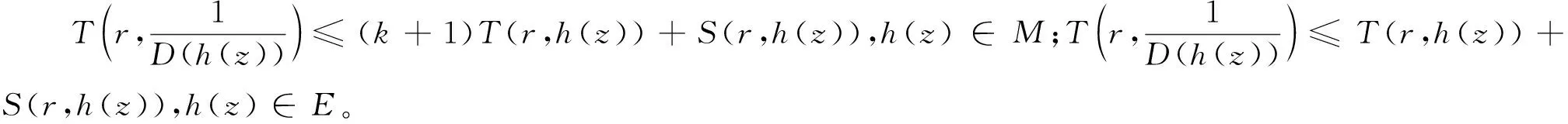
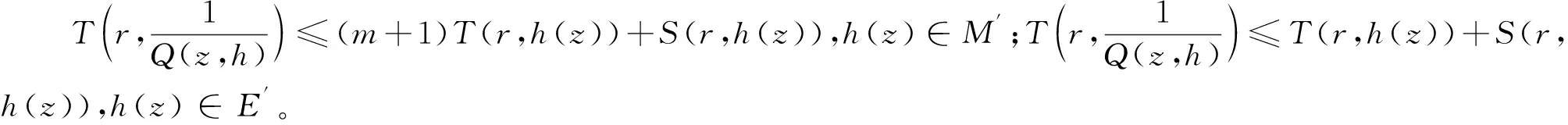
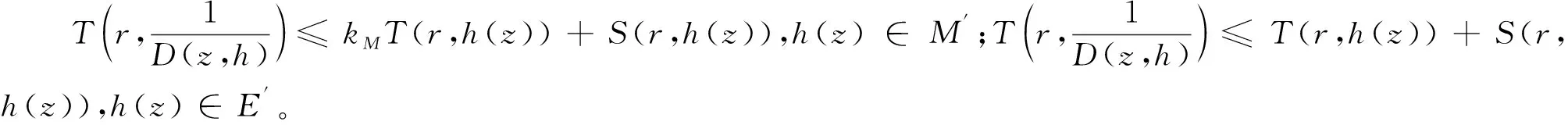
證明情形(1)可由引理2.1和Nevanlinna第一基本定理得到，情形(2)由引理2.2和Nevanlinna第一基本定理得到，情形(3)由引理2.1，引理2.2和Nevanlinna第一基本定理得到。

引理2.4如果f(z),g(z)∈M，則有

nT(r,f)-(k+1)T(r,g)≤T(r,P(f)D(g(z))+S(r,f)+S(r,g)≤nT(r,f)+(k+1)T(r,g)

(2.5)

如果f(z),g(z)∈E，則有

nT(r,f)-T(r,g)≤T(r,P(f)D(g(z))+S(r,f)+S(r,g)≤nT(r,f)+T(r,g)

(2.6)

證明我們僅給出亞純函數(shù)的情況，整函數(shù)的情況可類似證明。通過引理2.1可直接證得(2.5)右邊的不等式成立，接下來去證明(2.5)左邊的不等式。

由引理2.3(1)和Nevanlinna第一基本定理及Valiron-Mohon’ko定理[17，定理2.2.5]可得

利用引理2.4相同的證明方法可以得到下面的兩個(gè)引理：

引理2.5如果f(z),g(z)∈M′，則有

nT(r,f)-(m+1)T(r,g)≤T(r,P(f)Q(z,g))+S(r,f)+S(r,g)≤nT(r,f)+(m+1)T(r,g)

(2.7)

如果f(z),g(z)∈E′，則有

nT(r,f)-T(r,g)≤T(r,P(f)Q(z,g))+S(r,f)+S(r,g)≤nT(r,f)+T(r,g)

(2.8)

引理2.6如果f(z),g(z)∈M′，則有

nT(r,f)-kMT(r,g)≤T(r,P(f)D(z,g))+S(r,f)+S(r,g)≤nT(r,f)+kMT(r,g)

(2.9)

如果f(z),g(z)∈E′，則有

nT(r,f)-T(r,g)≤T(r,P(f)D(z,h))+S(r,f)+S(r,g)≤nT(r,f)+T(r,g)

(2.10)

設(shè)p是正整數(shù)且a∈，記

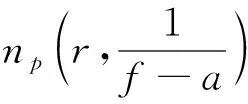
引理2.7[16]設(shè)f和g是非常數(shù)亞純函數(shù)，α(z)是f和g的非零小函數(shù)。如果α(z)是f和g的CM公共小函數(shù)，則f和g滿足下列三種情況之一：

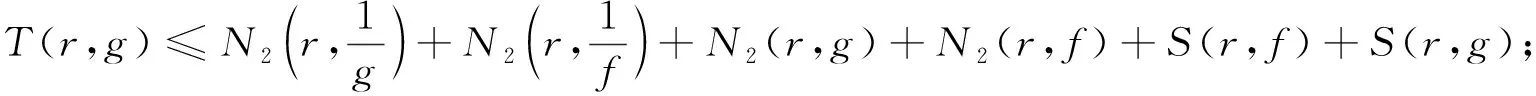
(ⅱ)f≡g；

(ⅲ)f·g=α2。

3 定理的證明

定理1.1的證明設(shè)f,g為超越亞純函數(shù)，令F=P(f)L(g)-a(z)，則

nm(r,f)=m(r,P(f))+S(r,f)=

(3.1)

且

nN(r,f)=N(r,P(f))+S(r,f)=

(3.2)

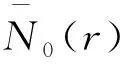
nT(r,f)≤T(r,F(z)+a(z))+

(3.3)

根據(jù)F(z)的表達(dá)式，我們有

利用Nevanlinna第二基本定理，可以得到

結(jié)合上面的不等式以及(3.3)，可得到

(3.4)

下面討論三種情況：

情形1如果L(g)=D(g(z))，結(jié)合引理2.3的(1)，則可以得到

設(shè)G=P(g)L(f)-a(z)，利用上述的方法可以得到

因此，結(jié)合上面的兩個(gè)不等式，我們可以得到

所以當(dāng)n≥t+k+3時(shí)，F(xiàn)(z)和G(z)至少有一個(gè)有無窮多個(gè)零點(diǎn)，即P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一個(gè)有無窮多個(gè)零點(diǎn)。

情形2設(shè)L(h)=Q(z,h)，結(jié)合引理2.3的(2)，利用情形1的方法，可以得到當(dāng)n≥t+m+3時(shí)，P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一個(gè)有無窮多個(gè)零點(diǎn)。

情形3設(shè)L(h)=D(z,h)，結(jié)合引理2.3的(3)，利用情形1的方法，可以得到當(dāng)n≥t+kM+2時(shí)，P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一個(gè)有無窮多個(gè)零點(diǎn)。

最后，如果f,g為超越整函數(shù)，則利用上述得到(3.4)的基本方法但要去掉極點(diǎn)的計(jì)數(shù)函數(shù)，可以得到

利用引理2.3中整函數(shù)時(shí)的特征函數(shù)估計(jì)式，便可得到定理1.1整函數(shù)情況下的結(jié)果。

定理1.2的證明

情形1設(shè)F(z)=P(f)D(g)，G(z)=P(g)D(f)。由于a(z)是F(z)和G(z)的CM公共小函數(shù)，利用引理2.2，2.3和2.6的(i)，可以得到

4N(r,g)]+S(r,f)+S(r,g)≤(2Γ0+2k+10)[T(r,f)+T(r,g)]+S(r,f)+S(r,g)

因?yàn)閚≥2Γ0+3k+12，所以引理2.6的(i)不會(huì)發(fā)生，因此有P(f)D(g)=P(g)D(f)或者P(f)D(g)P(g)D(f)=a(z)2。

情形2設(shè)F(z)=P(f)Q(z,g)，G(z)=P(g)Q(z,f)。由于a(z)是F(z)和G(z)的CM公共小函數(shù)，利用引理2.2，2.4和2.6的(i)，可以得到

(n-m-1)[T(r,f)+T(r,g)]≤

因?yàn)閚≥2Γ0+5m+6，故引理2.6的(i)不會(huì)發(fā)生。因此有P(f)Q(z,g)=P(g)Q(z,f)或者P(f)Q(z,g)P(g)Q(z,f)=a(z)2。

情形3設(shè)F(z)=P(f)D(z,g)，G(z)=P(g)D(z,f)。由于a(z)是F(z)和G(z)的CM公共小函數(shù)，利用引理2.2，2.5和2.6的(i)，可以得到

(n-kM)[T(r,f)+T(r,g)]≤(2Γ0+2kM+4m+4)(T(r,f)+T(r,g))+S(r,f)+S(r,g)

因?yàn)閚≥2Γ0+3kM+4m+5，故引理2.6的(i)不會(huì)發(fā)生，因此有P(f)D(z,g)=P(g)D(z,f)或P(f)D(z,g)P(g)D(z,f)=a(z)2。

4 討論

函數(shù)型復(fù)微分方程的解的性質(zhì)研究是個(gè)有趣的課題，最近的研究可參見[20]，本文中，當(dāng)f(z)，g(z)為超越整函數(shù)時(shí)，觀察方程

P(f)L(g)P(g)L(f)=a(z)2

(4.1)

由Nevanlinna第二基本定理可知P(z)至多有一個(gè)零點(diǎn)，即P(z)=a(z-b)n，其中a為非零常數(shù)，b為常數(shù)。然而，當(dāng)f(z)，g(z)為超越亞純函數(shù)時(shí)，情況變得復(fù)雜。進(jìn)一步觀察方程

P(f)L(g)=P(g)L(f)

(4.2)

如果上面兩個(gè)方程中L(h)取特殊表達(dá)式，比如L(h)=h′(z)或者h(yuǎn)(z+c)，部分討論可參見[15,19]，然而其他情況的研究面臨較大困難，即使L(h)=h′(z+c)，都無法從方程f(z)ng′(z+c)=g(z)nf′(z+c)中得到f(z)和g(z)的所有關(guān)系式，雖然f(z)=g(z)或者f(z)=tg(z)，tn-1=1滿足上述方程。因此，如何從方程(4.1)和(4.2)中尋求f(z)和g(z)準(zhǔn)確關(guān)系值得深入研究。