基于虛擬旋轉坐標系的瞬時功率因數檢測及補償方法

蘆 浩，章軍華，姜瑤瑤，粟忠來

（1.國網浙江淳安縣供電有限公司，浙江 淳安 311700；2.淳安縣電力實業有限公司，浙江 淳安 311700；3.許繼集團有限公司，河南 許昌 461000）

0 引言

電力系統中較低的功率因數將影響電力系統的經濟、安全可靠運行[1-3]。對于供電穩定性要求較高的制造設備，功率因數的變化將直接影響其制造精度及產品合格率，因此穩定電力系統的功率因數極其重要。在輸配電系統中提高功率因數的設備主要有固定電容器與動態補償器[4-7]，其中動態補償器具有響應速度快、補償效果好及補償多樣性等優點，目前已經得到廣泛應用[8-11]。

功率因數的實時、準確檢測，是動態補償器快速、高精度補償的前提[12-14]。目前，動態補償器提高功率因數的主要手段是無功功率的補償。動態補償器無功功率檢測方法主要有：基于瞬時無功功率理論的諧波檢測方法和基于時域的TTA（測度時間增強）諧波檢測方法[15-16]。基于瞬時無功功率理論的無功功率及諧波檢測方法需要對電壓進行鎖相，運算量較大，造成檢測延時較大，從而影響無功功率跟蹤補償效果，而且鎖相精度也直接影響無功檢測的精度[17]。基于時域的TTA諧波檢測方法動態響應較快，可以檢測出多種分量[18]，但是仍然需要電壓鎖相環節，無法避免電壓畸變以及電壓鎖相精度低造成諧波檢測精度降低的問題。以上兩種方法均是通過無功功率檢測和補償間接提高功率因數，并未給出功率因數實時檢測及恒定功率因數補償的方法。在礦熱爐、黃金冶煉、電解鋁等行業，設備制造工藝對功率因數較為敏感，功率因數改變時需要調節進料速度及電極間距等參數[19]。傳統補償算法盡管可實現較高功率因數，但是實時波動的功率因數將對制造精度及產品合格率造成較大影響，因此恒定的功率因數補償極其重要。

本文提出一種基于虛擬旋轉坐標系的瞬時功率因數檢測及補償方法。首先，介紹將負載電流和系統電壓信號分解到虛擬旋轉坐標系的方法，并給出瞬時功率因數實時檢測方法，此過程省去電壓鎖相運算環節，避免了電壓畸變以及電壓鎖相精度低造成諧波檢測精度降低的問題。其次，以恒定的功率因數作為控制目標，獲得補償的實時電流值，動態補償器根據該實時電流值進行相應補償后可實現瞬時功率因數補償。然后，對補償后的系統電流進行瞬時功率因數檢測，以恒定的功率因數作為控制目標進行閉環控制，從而實現恒定的功率因數控制。最后，結合理論計算、仿真分析和工程應用實例，對所提方法的正確性進行驗證。

1 傳統功率因數檢測及補償的原理

目前動態補償器常采用以三相電路瞬時無功功率理論為基礎的ip-iq檢測方法作為提高功率因數的方法，其原理如圖1 所示。該方法需要用到與ea同相位的正弦信號sin ωt、余弦信號-cos ωt和PLL[20]，因此檢測精度受PLL 精度、處理器運算速度等因素影響。并且該方法并未給出功率因數實時直接檢測及恒定功率因數補償的方法，并不適用于恒定功率因數補償的場合。

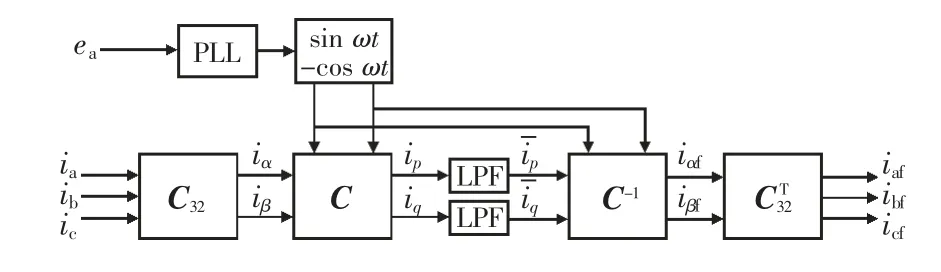
圖1 ip-iq 檢測方法的原理框圖

2 虛擬旋轉坐標系的功率因數檢測及補償方法

2.1 虛擬旋轉坐標系的建立

設瞬時電流為i，虛擬旋轉坐標系由p1，q1軸組成，基波旋轉角頻率ω1=2πf1（f1為基波頻率），p1軸與α 軸的虛擬旋轉夾角為θ1。將瞬時電流i分解到αβ 坐標系獲得iα，iβ，分解到虛擬旋轉坐標系獲得i1p，i1q，如圖2 所示，其中，i1pα，i1qα分別為i1p和i1q在α 軸的分量，i1pβ，i1qβ為分別為i1p和i1q在β 軸的分量。

圖2 虛擬旋轉坐標系

2.2 瞬時功率因數檢測及補償方法

虛擬旋轉坐標系的瞬時功率因數檢測及補償方法原理如圖3 所示，其中的量符號均在后文計算中進行說明。首先，利用基波頻率f1、時間t 構造旋轉角θ1及變換矩陣C1，提取三相負載基波正序電流。然后，根據負載基波正序電流實時計算負載功率因數FL、有功電流ILp、無功電流ILq進行。然后，根據負載相關瞬時值FL，ILp，ILq和目標功率因數Fref進行功率因數控制，并獲得動態補償器的補償指令。整個檢測過程無需電壓鎖相環節，避免了鎖相精度引起的檢測精度問題，并且以目標功率因數作為控制目標可實現功率因數的恒定控制。最后，為了降低動態補償器輸出誤差造成補償后的功率因數與目標功率因數偏差問題，該方法中還加入了系統功率因數檢測及閉環控制環節，可進一步提高恒定功率因數補償精度。

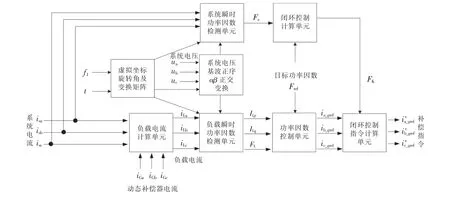
圖3 虛擬旋轉坐標系的檢測方法原理框圖

p1軸與α 軸的虛擬旋轉夾角θ1計算公式為：

式中：θ0為初始相角，可以為任意值，與系統電壓鎖相角無關。

虛擬旋轉坐標系變換矩陣C1可表示為：

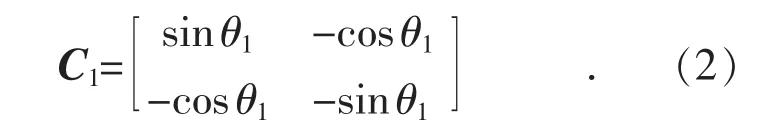
由系統瞬時電流isa，isb，isc和動態補償器輸出瞬時電流iGa，iGb，iGc可計算出三相負載瞬時電流iLa，iLb，iLc。

三相負載瞬時電流iLa，iLb，iLc由Clark 正 變換C32轉化到αβ 靜止坐標系，轉換方法為：

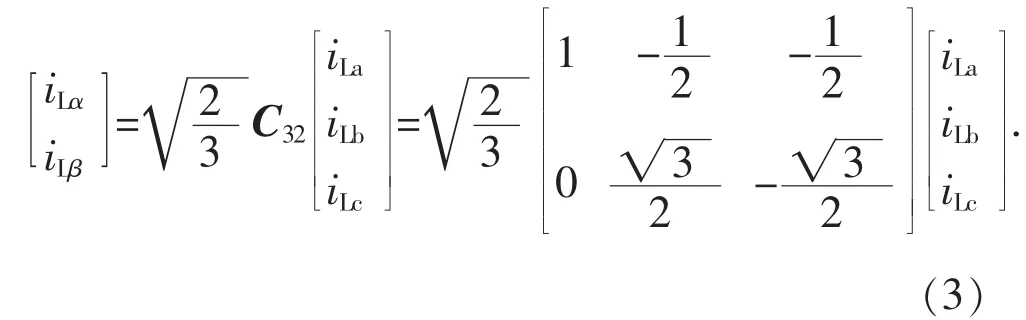
將αβ 坐標系獲得的分量經過虛擬旋轉坐標系變換矩陣C1轉化到虛擬旋轉坐標系的p1，q1軸，從而獲得正序分量i1p，i1q：

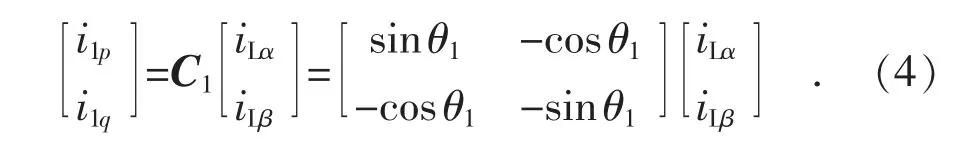
i1p，i1q分量由直流分量與諧波分量組成，經由低通濾波后可得直流分量可計算負載電流正序幅值IL1：

同理，可獲取三相系統電壓在αβ 坐標系下的基波分量u1αf，u1βf。

結合瞬時無功功率理論[12]，由負載電流基波分量i1αf，i1βf與系統電壓基波分量u1αf，u1βf可計算負載瞬時有功功率PL和瞬時無功功率QL：

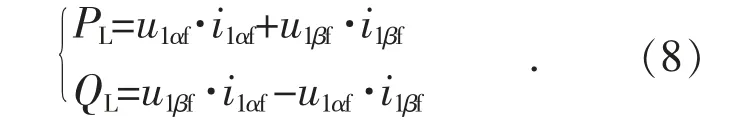
由PL，QL可計算負載瞬時功率因數FL：

為了進行恒功率因數補償，由式（5）和式（9）可計算出負載有功電流幅值ILp和無功電流幅值ILq：

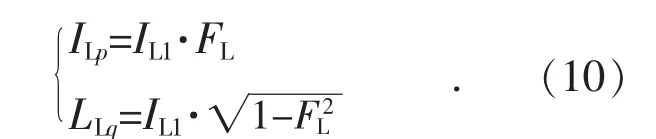
根據負載相關瞬時值FL，ILp，ILq和目標功率因數Fref可計算恒定功率因數控制的實時控制量Iqref：

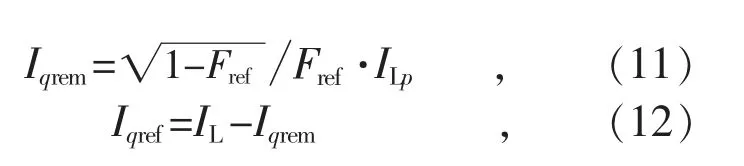
式中：Iqrem為恒定功率因數控制后系統剩余無功電流。

為了獲得動態補償器瞬時控制指令，由實時控制量Iqref與系統三相鎖相角可以轉換成瞬時可控制量ia_qref，ib_qref，ic_qref[20]。

為了降低動態補償器輸出誤差造成補償后的功率因數與目標功率因數偏差問題，補償方法中加入了閉環控制。根據式（3）—（9）可計算補償后系統瞬時功率因數Fs，Fs與目標功率因數Fref進行PID 或模糊PID 等控制后獲得閉環調節控制量FK，閉環控制后的動態補償指令為：

通過以上方法可獲得負載側與系統側的瞬時功率因數的實時檢測以及恒定功率因數補償的閉環控制指令，動態補償器利用該指令跟蹤補償后可實現穩定功率因數的目的。

2.3 瞬時功率因數檢測方法的分析

設三相電壓瞬時值ua，ub，uc可表示為：

式（19）與式（5）計算的基波正序幅值結果一致。

將式（18）按式（7）反變換后可獲得αβ 坐標系下的負載電流基波分量i1αf，i1βf：

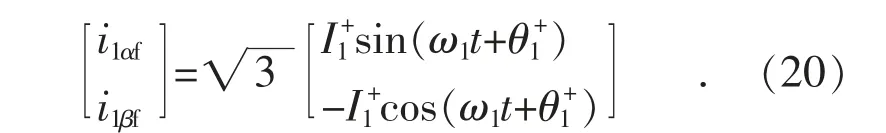
同理，由式（3）—（7）可獲取三相系統電壓在αβ 坐標系下的基波分量u1αf，u1βf：

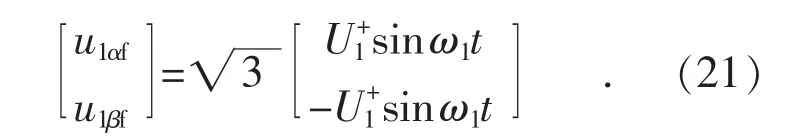
由式（8）—（9）可計算瞬時功率因數FL：

由式（22）可知，通過理論分析，本文瞬時功率因數檢測方法可實時檢出基波正序功率因數。

通過式（14）—（22）進一步分析可知：

（1）該檢測方法中無電壓鎖相環節，虛擬旋轉角θ1無需與系統電壓保持同相位（相位差θ0可取任意值），即可實現瞬時功率因數的實時計算。

（2）該方法的分析中電壓與電流均疊加了各次諧波和負序分量，經過虛擬坐標變換后，可以獲取αβ 坐標系下的負載電流基波分量i1αf，i1βf和電壓基波分量u1αf，u1βf，最終計算的瞬時功率因數為基波正序的功率因數。系統中負序分量和諧波分量可通過動態補償器進行補償，最終系統中將只剩下正序有功和無功分量，因此目前動態補償器提高功率因數時通常只需考慮基波正序無功功率和基波正序功率因數。本方法檢測的功率因數為基波正序的功率因數，對于畸變場合該方法仍然可以作為動態補償器瞬時功率因數檢測和治理的方法。

海綿城市是指城市如同海綿一樣，在蓄水方面可以體現出良好的彈性，該理念是在2012年低碳城市論壇上首次被提出。我國古代的坡搪系統、三角洲的桑基魚搪系統等體現了人類的生存智慧：將水作為財，就地蓄留、就地消化旱澇問題，“海綿”的哲學即是就地調節旱澇。開展海綿城市建設是解決目前我國城市水環境面臨的“逢雨必澇、雨停即旱”、雨水徑流污染、水資源短缺等問題的有效涂徑。

3 仿真驗證

利用MATLAB 搭建10 kV 鏈式STATCOM（靜止同步補償器）仿真模型驗證上述方法，模型主要參數：系統電壓10 kV，頻率50 Hz，0 s 時投入負載1（有功功率2 MW，感性無功功率1.5 Mvar），0.18 s 時投入負載2（有功功率2 MW，容性無功功率3 Mvar）。運用本文的瞬時功率檢測及補償方法對STATCOM 進行控制，0.6 s 開始以目標功率因數Fref=0.98 進行補償，0.12 s 時設定Fref=1.0。

圖4 為本文方法檢出負載功率及功率因數曲線。0 s 時投入負載1，功率因數理論計算值為0.8；在負載1 投入基礎上，0.18 s 時投入負載2，功率因數理論計算值為0.936 3。圖4（a）仿真分析的瞬時功率因數、功率均與理論計算值一致。圖4（b）中負載0 s 投入后即可實時計算出負載功率因數，進一步說明本方法可快速地實時檢測功率因數。

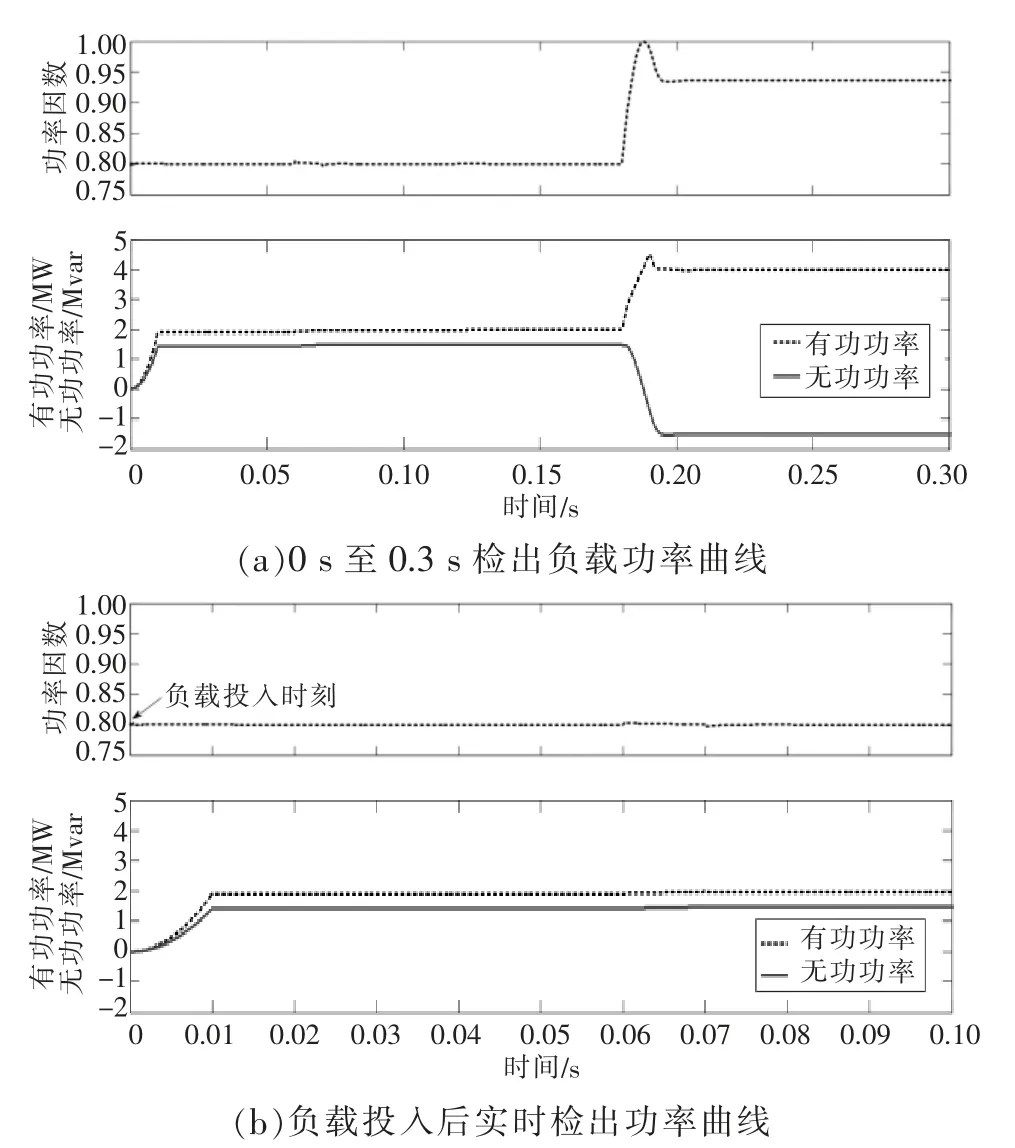
圖4 本文方法檢出負載功率曲線

圖5 為動態補償器補償前后功率曲線，圖6為系統電壓、電流與動態補償器輸出電流波形。可以看出，利用本文方法的動態補償器補償后能很好地穩定系統功率因數，并且在改變負載或目標功率因數改變時均能實現快速跟蹤補償。

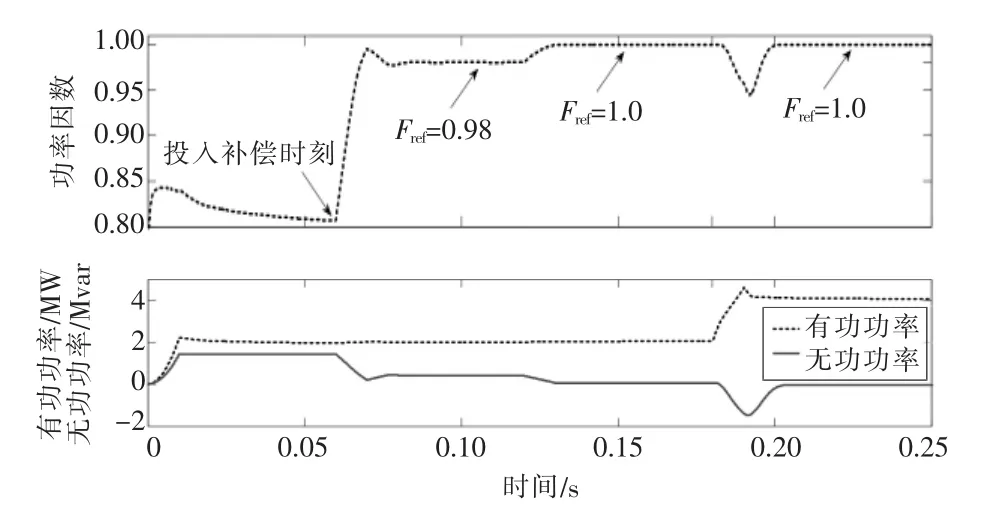
圖5 補償前后系統功率曲線

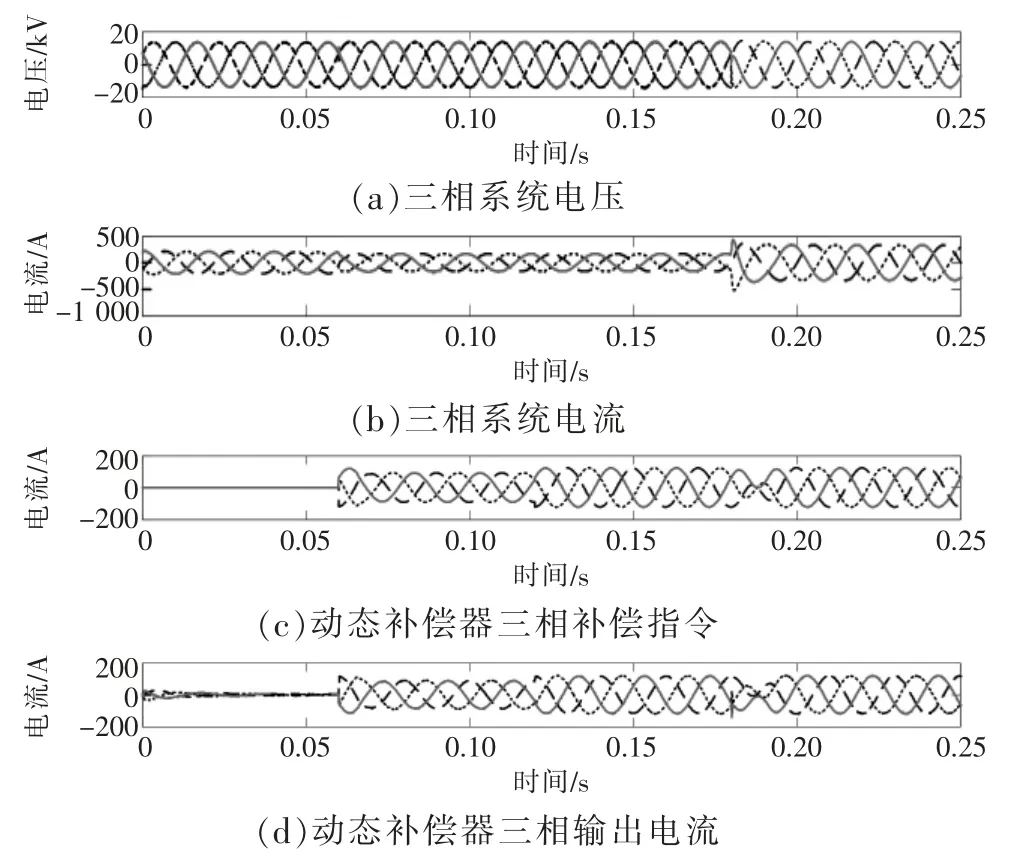
圖6 補償前后系統電壓、電流及動態補償器電流波形

為了進一步驗證本文方法在電流畸變場合的有效性，在以上仿真模型基礎上，0 s 時投入三相整流負載，整流直流側接入61.44 Ω 電阻負載。0.6 s 開始動態補償器采用本文方法與諧波補償方法相結合的方式對系統進行恒定功率因數補償和諧波治理。

圖7 為電流畸變時本文方法檢出負載功率及瞬時功率因數曲線。各階段檢出負載瞬時功率因數與理論計算值保持一致，進一步說明本文方法在畸變場合仍然能準確檢測瞬時功率因數。

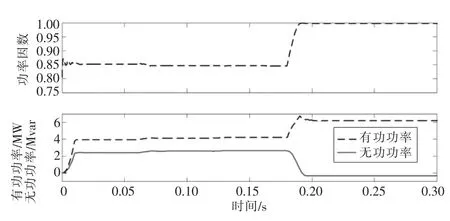
圖7 電流畸變時，本文方法檢出負載功率曲線

圖8 為電流畸變時動態補償器補償前后功率曲線，圖9 為系統電壓、電流與動態補償器輸出電流波形。可以看出，本文方法可實現功率因數的恒定控制。

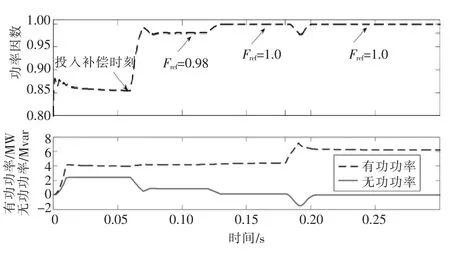
圖8 電流畸變率時，補償前后系統功率曲線

由圖4 至圖9 可知：本文方法可快速地實時檢測出功率因數；利用本文的瞬時功率因數檢測與補償方法，動態補償器可較好地穩定系統功率因數；對于電流畸變場合，本文方法仍可快速準確檢測瞬時功率因數，并可結合其他補償方法（如諧波補償方法），實現電能質量的綜合治理。仿真結果與理論計算值保持一致，驗證了本文方法的有效性。

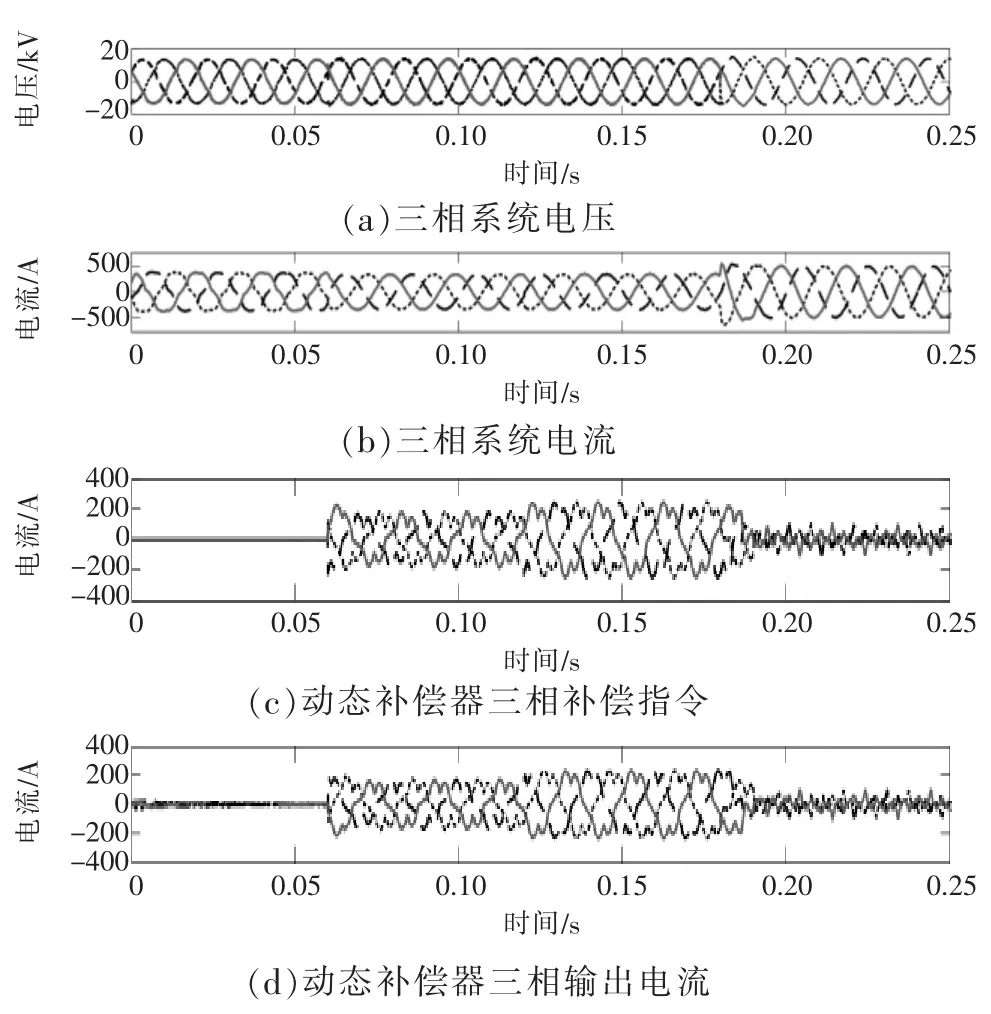
圖9 電流畸變時，補償前后電壓、電流波形

4 工程應用分析

將上述檢測方法應用在10 kV，3 Mvar 鏈式STATCOM 中，如圖10 所示，應用場合為某精密機械加工企業。現場無功功率1.1～1.3 Mvar，系統電流總諧波畸變率6%～7.6%，系統電壓總諧波畸變率1.35%～1.65%，基波頻率波動范圍49.9～50.1 Hz，系統電流不平衡度3%，設備投入后進行恒定功率因數補償。

圖10 現場參數及應用

圖11 為設備投運前三相電流波形及諧波分析，電流畸變率達到6.5%。

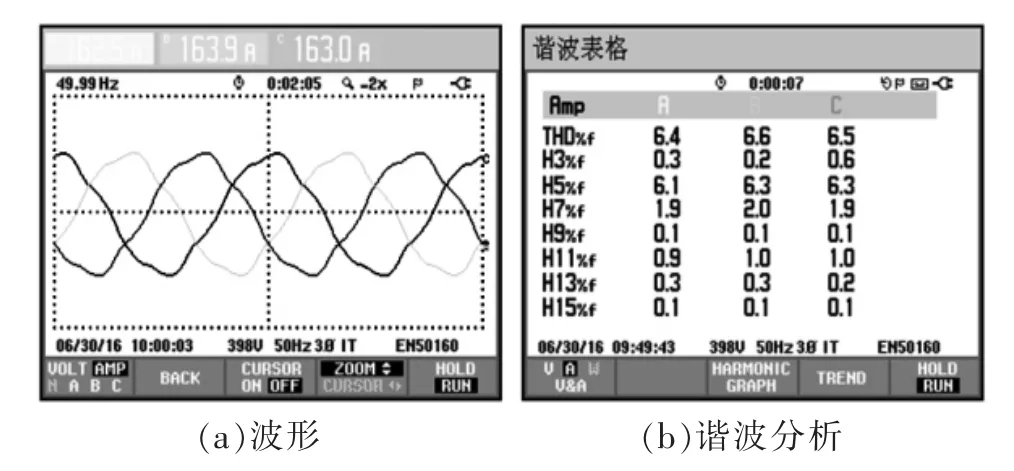
圖11 設備投運前三相電流波形及諧波分析

圖12 為設備投運前系統功率分析，最小功率因數為0.88，最大功率因數為0.92。

圖12 設備投運前系統功率分析

圖13 為鏈式STATCOM 運用本文方法補償后，對系統功率因數進行恒定功率因數補償，目標功率因數Fref分別設為1.0 和0.98。盡管電流存在畸變，補償后系統功率因數與目標功率因數一致。實際工程應用結果進一步驗證了本文方法的正確性和有效性。

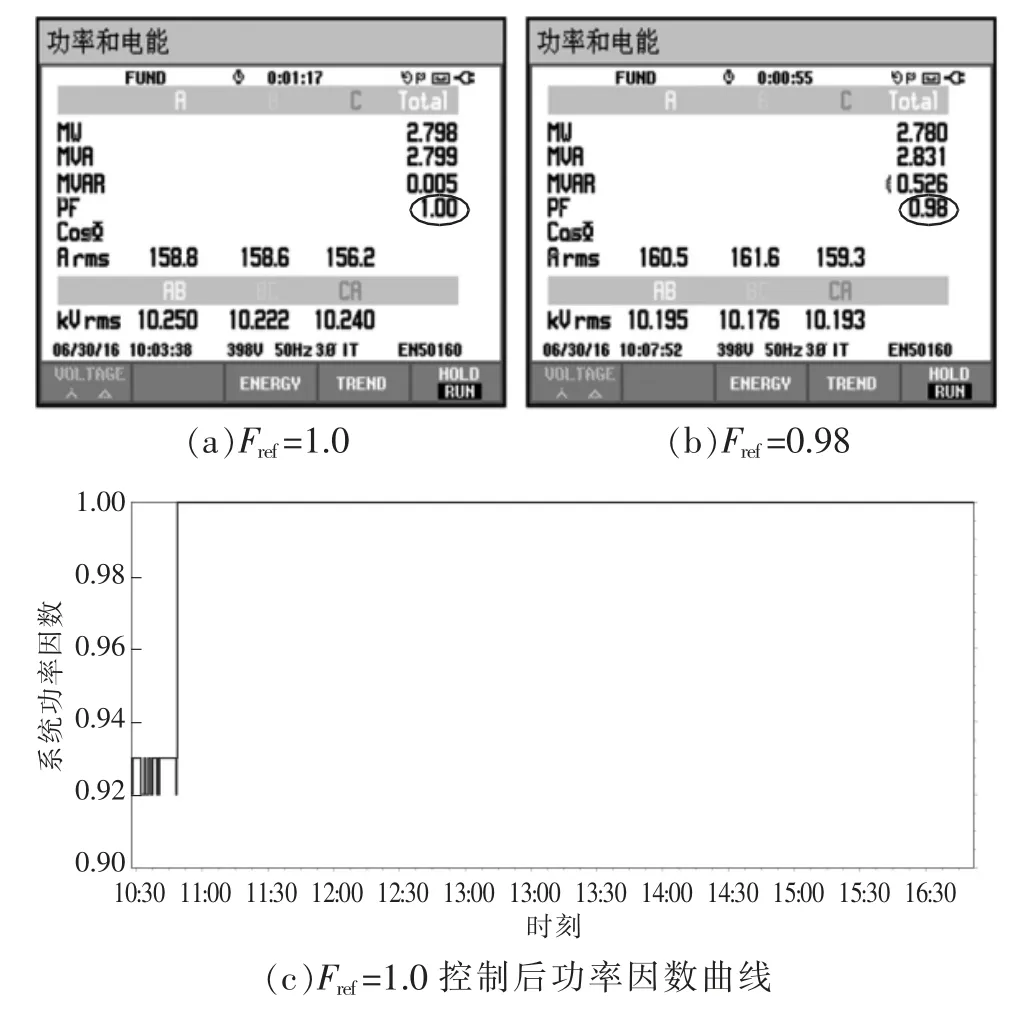
圖13 采用本文方法進行恒定功率因數補償后的功率分析

5 結語

對于礦熱爐、黃金冶煉、電解鋁等行業，功率因數的變化將直接影響其制造精度及產品合格率，因此穩定電力系統的功率因數極其重要。本文分析了傳統功率因數補償方法的原理，結合常見補償方法存在的問題，提出一種基于虛擬旋轉坐標系的瞬時功率因數檢測及補償方法。該方法采用虛擬旋轉坐標系和瞬時功率因數檢測方法對功率因數進行實時檢測，避免了原有方法電壓畸變以及電壓鎖相精度低造成檢測精度降低的問題。并且，以恒定的功率因數作為控制目標，實現了恒定的功率因數閉環控制。理論計算、仿真分析和工程應用結果均驗證了該檢測方法的正確性和可行性。本文方法對于電壓和電流畸變的場合，仍然可實現瞬時功率因數的準確檢測和補償控制。本文方法結合其他補償算法，也可實現電能質量的綜合治理。