基于增廣P型學(xué)習(xí)觀測器的航天器故障重構(gòu)和自適應(yīng)容錯控制

駱天依 李化義 孟慶松

0 引言

姿態(tài)控制系統(tǒng)作為航天器最重要的子系統(tǒng)之一,由于所處空間具有復(fù)雜不確定性,極易發(fā)生故障,導(dǎo)致航天器失去穩(wěn)定性甚至完全失效[1-3]．因此,很有必要對航天器發(fā)生的故障及時進(jìn)行診斷和隔離,并設(shè)計出新的容錯控制器保證航天器在軌運行期間的可靠性與安全性．

按照Frank等[4]的觀點,故障診斷方法可以分為三類:基于解析模型的方法、基于信息處理的方法和基于知識的方法．其中,基于解析模型的方法作為傳統(tǒng)的故障診斷方法,經(jīng)過近50年的發(fā)展和完善,至今仍被廣泛應(yīng)用在航天器姿控系統(tǒng)故障重構(gòu)和容錯控制領(lǐng)域．然而隨著航天任務(wù)難度的提升,航天器的結(jié)構(gòu)和功能趨向于復(fù)雜多樣化,構(gòu)成航天器的元器件種類和數(shù)量不斷增加,這也提高了故障診斷方法的復(fù)雜性和容錯控制器的設(shè)計難度．但仍有很多學(xué)者在此領(lǐng)域進(jìn)行著不斷的探索和突破．

針對航天器執(zhí)行機(jī)構(gòu)故障,Li等[5]設(shè)計了擴(kuò)張狀態(tài)觀測器對航天器姿控系統(tǒng)模型參數(shù)、外在干擾和執(zhí)行器的飽和輸出進(jìn)行估計和補(bǔ)償,并利用逆最優(yōu)控制李雅普諾夫函數(shù)方法保證閉環(huán)系統(tǒng)的漸近穩(wěn)定性;Zhang等[6]針對剛性航天器執(zhí)行機(jī)構(gòu)失效故障和飽和約束,設(shè)計了一種滑模故障估計觀測器,并在此基礎(chǔ)上利用滑模控制思想設(shè)計了相應(yīng)的容錯控制器;Wang等[7]首先利用自適應(yīng)方法估計執(zhí)行器故障模型中的未知參數(shù),在此基礎(chǔ)上設(shè)計出一種自適應(yīng)未知輸入觀測器對故障進(jìn)行檢測和隔離．

針對航天器傳感器故障,Wang 等[8]基于線性矩陣不等式技術(shù)設(shè)計出兩組具有良好魯棒性的H∞最優(yōu)觀測器,并設(shè)計出滿足一定姿態(tài)誤差精度的PD控制器(Proportional-Derivative controller)保障航天器在陀螺和傳感器故障同時發(fā)生情況下的安全穩(wěn)定運行能力;韓冰[9]對基于擴(kuò)張狀態(tài)觀測器的方法進(jìn)行了改進(jìn),并利用動態(tài)輸出反饋的方法,提高了故障系統(tǒng)的控制性能;江耿豐等[10]對常用的衛(wèi)星測量部件光學(xué)敏感器和慣性敏感器分別設(shè)計了隔離觀測器和Kalman濾波器,通過比較兩個觀測器的輸出殘差,達(dá)到故障診斷和隔離的目的．

基于上述研究,本文提出了一種基于增廣P型迭代學(xué)習(xí)觀測器的航天器傳感器故障重構(gòu)方法,并利用自適應(yīng)積分滑模的思想設(shè)計新的控制器,解決了對航天器姿控系統(tǒng)故障容錯控制問題．最后,通過航天器姿控系統(tǒng)仿真實例驗證了本文所設(shè)計觀測器和控制器的有效性．

1 問題描述

1.1 航天器姿控系統(tǒng)模型

考慮如下三軸穩(wěn)定剛體衛(wèi)星的姿態(tài)運動學(xué)與動力學(xué)模型:

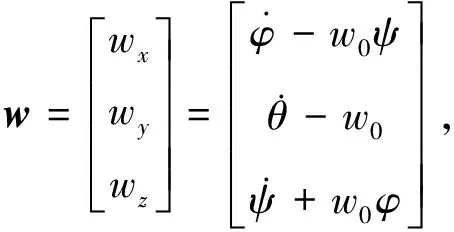
(1)

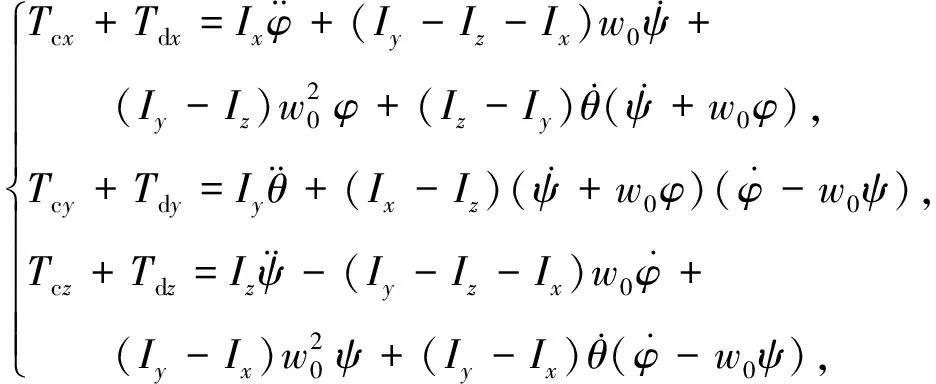
(2)

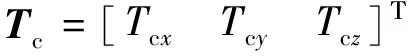
定義

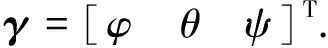
(3)

忽略二階小量對系統(tǒng)模型的影響,動力學(xué)模型可以轉(zhuǎn)換成如下微分方程的形式:

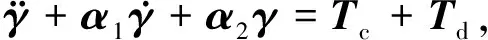
(4)

其中參數(shù)矩陣α1和α2表示如下:

令

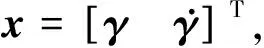
(5)

能夠得到如下形式的航天器姿控系統(tǒng)狀態(tài)空間模型:

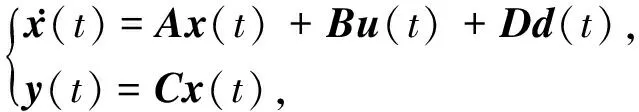
(6)

其中u(t)=Tc表示控制輸入,d(t)=Td表示干擾輸入．

1.2 問題描述

現(xiàn)考慮如下含有不確定干擾輸入的傳感器故障模型:

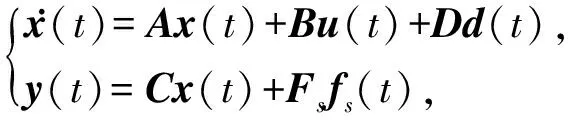
(7)

其中x(t)∈Rn,u(t)∈Rm,y(t)∈Rr分別表示系統(tǒng)狀態(tài)向量、輸入向量和輸出向量，fs(t)∈Rq和d(t)∈Rr0分別表示航天器陀螺儀故障和受到的未知干擾，A,B,C,D均為適當(dāng)維數(shù)的系數(shù)矩陣,A∈Rn×n,B∈Rn×m,C∈Rr×n,D∈Rn×r0,且滿足r0≤r．

對于式(7)所示的傳感器故障,為了抑制故障輸出對系統(tǒng)可靠性的干擾,可以設(shè)計如下形式的輸出濾波器:

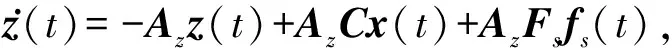
(8)

其中系數(shù)矩陣Az∈Rr×r是一個穩(wěn)定矩陣,所有特征值均具有負(fù)實部．

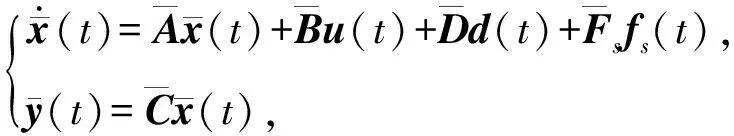
(9)

其中

本文的目的之一就是針對傳感器故障增廣系統(tǒng)(9)設(shè)計增廣P型學(xué)習(xí)觀測器,使得傳感器故障能夠?qū)崿F(xiàn)精確重構(gòu)．

同時,為了改善故障系統(tǒng)的性能指標(biāo),減輕陀螺儀故障對航天器姿控系統(tǒng)的不利影響,本文在實現(xiàn)故障重構(gòu)的基礎(chǔ)上,基于故障模型(7),進(jìn)一步設(shè)計容錯控制器,保證航天器在故障狀態(tài)下的穩(wěn)定運行能力．

2 基于增廣P型學(xué)習(xí)觀測器的故障重構(gòu)

針對傳感器故障增廣系統(tǒng)(9),考慮如下形式的增廣P型學(xué)習(xí)觀測器:

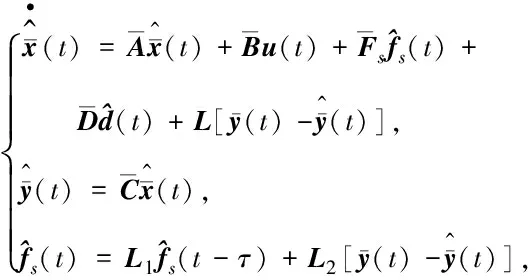
(10)

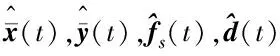
定義幾種誤差變量如表1所示．

表1 增廣P型觀測器設(shè)計所需誤差變量

考慮增廣系統(tǒng)(9)及其增廣P型學(xué)習(xí)觀測器(10),根據(jù)表1,可得誤差系統(tǒng)動態(tài)方程:

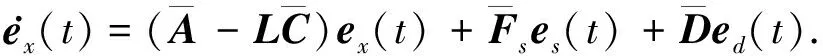
(11)

給出以下假設(shè)輔助增廣P型故障重構(gòu)觀測器的設(shè)計:

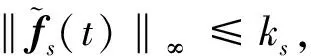
(12)

根據(jù)假設(shè)1和表1,能夠得到如下傳感器故障重構(gòu)誤差方程:

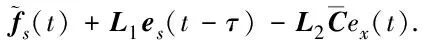
(13)

引理1[11]若傳感器故障重構(gòu)誤差如表1所示,則有以下不等式:

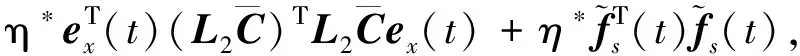
(14)

其中η*在定理1中給出．

定理1對于增廣系統(tǒng)(9)及其增廣P型學(xué)習(xí)觀測器(10),若存在下列不等式,則所設(shè)計的增廣P型學(xué)習(xí)觀測器能夠使系統(tǒng)狀態(tài)估計誤差ex(t)、干擾估計誤差ed(t)和傳感器故障重構(gòu)誤差es(t)一致漸近穩(wěn)定．

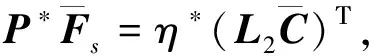
(15)

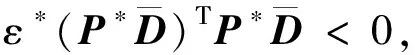
(16)

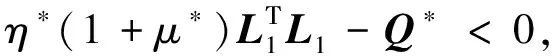
(17)

其中矩陣P*,Q*,參數(shù)δ*,ε*,η*,μ*的定義在證明過程中給出．

證明構(gòu)造Lyapunov函數(shù)

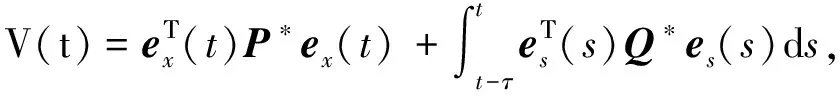
(18)

其中P*∈Rn,Q*∈Rm為正定的實對稱矩陣．

將式(18)對時間t求導(dǎo),得到:

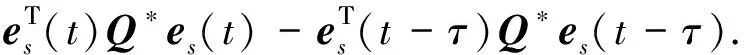
(19)

引理2[12]設(shè)x,y是具有適當(dāng)維數(shù)的實向量,A,B(t)是具有適當(dāng)維數(shù)的實矩陣,‖B(t)‖≤r,存在任意正數(shù)ε,有

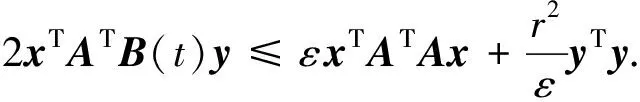
(20)

根據(jù)引理2,有:

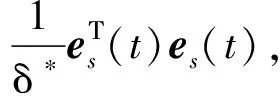
(21)

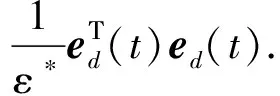
(22)

將式(21)和式(22)代入到式(19)中,并借助引理1,得到:

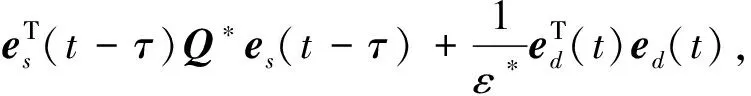
(23)

其中

η*=(1+σ*)λmax(Q*),

σ*≥0.

將式(13)代入式(23),并化簡得到:

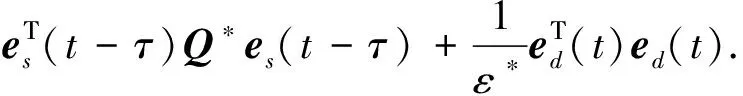
(24)

對于式(24),如果定理1中的式(15)成立,則有:

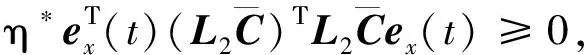
(25)

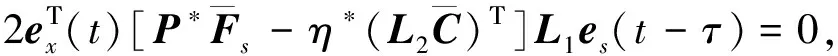
(26)

(27)

將式(25)—(27)代入到式(24)中,得到:

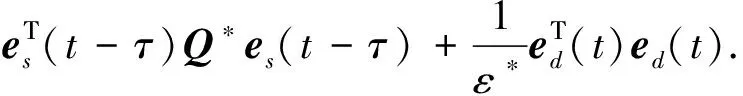
(28)

根據(jù)引理2,有:

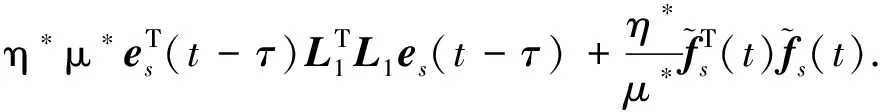
(29)

將式(29)代入到式(28)中,有以下不等式成立:

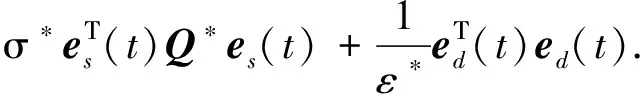
(30)

根據(jù)定理1中式(16)和式(17)可知:

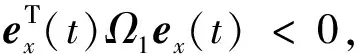
(31)

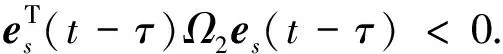
(32)

所以有:

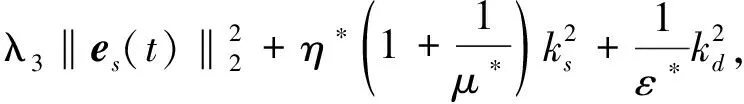
(33)

其中

將式(33)進(jìn)一步簡化,得到:

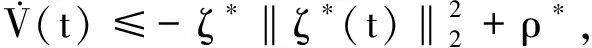
(34)

其中

根據(jù)式(34)可知,當(dāng)不等式滿足

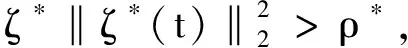
(35)

能夠得到:

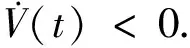
(36)

根據(jù)Lyapunov穩(wěn)定性理論,系統(tǒng)狀態(tài)估計誤差ex(t),干擾估計誤差ed(t)和傳感器故障重構(gòu)誤差ed(t)一致漸近穩(wěn)定．定理證畢．

由于定理1求解較為復(fù)雜,為計算定理1中的式(15)—(17),給出以下引理:

引理3[13]設(shè)

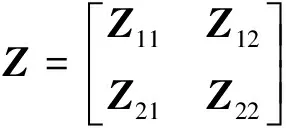
(37)

為對稱陣,則Z>0的充要條件是:

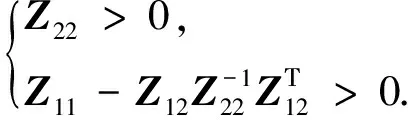
(38)

引理4[14]對于給定矩陣A∈Rn,當(dāng)且僅當(dāng)存在對稱矩陣P∈Rn滿足

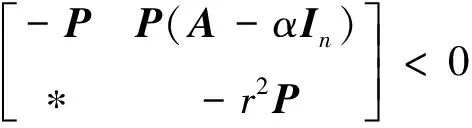
(39)

時,矩陣A的所有特征值能夠位于圓形穩(wěn)定域D(α,r)內(nèi)．其中α和r分別表示該穩(wěn)定圓的圓心和半徑．

利用引理3和引理4,將式(15)—(17)轉(zhuǎn)換為線性矩陣不等式形式:

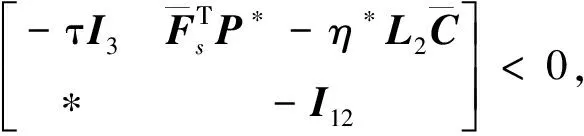
(40)

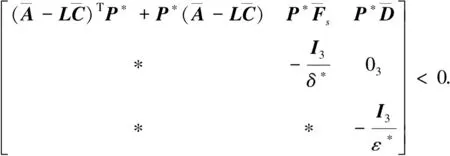
(41)

(42)

其中α和r分別表示該穩(wěn)定圓的圓心和半徑．

至此,增廣P型學(xué)習(xí)觀測器設(shè)計完成．

3 基于自適應(yīng)積分滑模的主動容錯控制

令

(43)

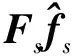
定義如下形式的積分滑模面:

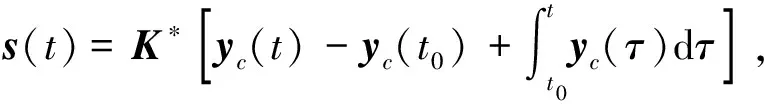
(44)

其中矩陣K*=(CB)+∈R3×6,yc(t0)表示系統(tǒng)初始時刻的實際輸出．采用這種積分滑模面可以使系統(tǒng)快速到達(dá)滑模面,提高系統(tǒng)的魯棒性能．

對積分滑模面(44)求導(dǎo),得到:

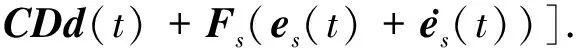
(45)

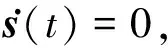
ueq(t)=-B+(A+I)x(t)-B+Dd(t)-

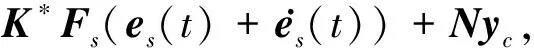
(46)

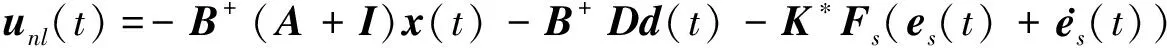
將等效控制律(46)代入到系統(tǒng)(7)中,得到如下形式的積分滑模狀態(tài)方程:

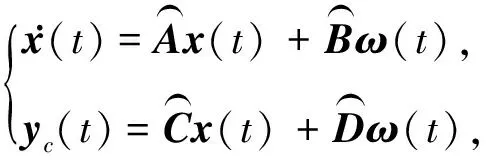
(47)

其中

定理2對于傳感器故障系統(tǒng)(7),設(shè)計形如式(48)所示的容錯控制律,能夠保證系統(tǒng)的漸近穩(wěn)定性．

u(t)=unl(t)+ul(t),

(48)

其中

其中λ*是選取的正常數(shù)．

被估計的未知參數(shù)ρ表達(dá)式為

(‖K*NFs‖+‖K*Fs‖)‖es(t)‖,

(49)

其自適應(yīng)律為

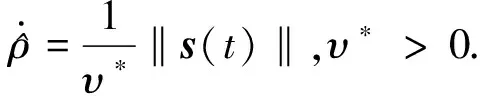
(50)

為求解定理2中的輸出反饋增益矩陣N,給出以下輔助引理．

引理5[15]對于形如式(51)的線性系統(tǒng),若存在正定對稱矩陣P使得式(52)成立,則線性系統(tǒng)(51)漸近穩(wěn)定．

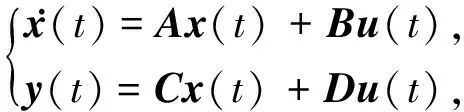
(51)

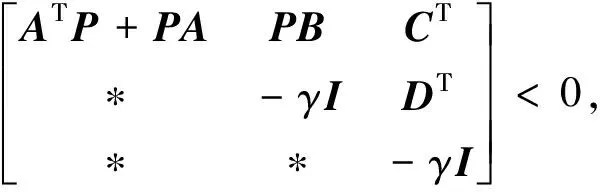
(52)

其中γ為一個任意給定的正常數(shù),I為適當(dāng)維數(shù)的單位陣．

證明首先,對于航天器姿控系統(tǒng)陀螺故障情況下的狀態(tài)空間模型(47),利用引理5能夠得到形如式(53)所示的不等式,使得系統(tǒng)(47)漸近穩(wěn)定．

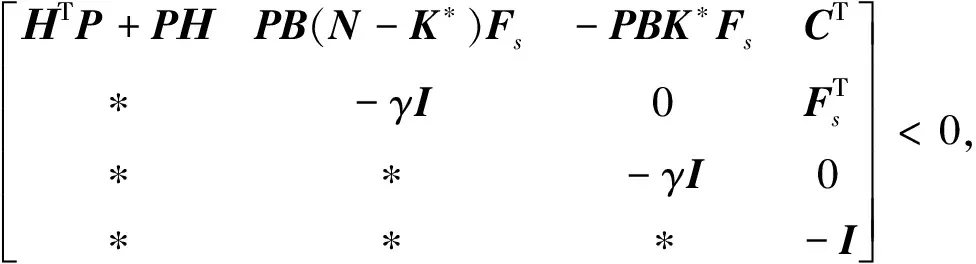
(53)

其中H=BNC-I．矩陣P和N可以通過LMI工具箱求解得到．

然后,定義形如式(54)的Lyapunov函數(shù),利用Lyapunov穩(wěn)定性理論,證明整個系統(tǒng)在故障重構(gòu)后的漸近穩(wěn)定性．

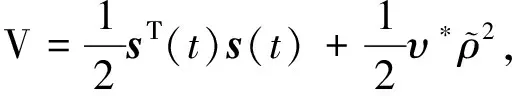
(54)

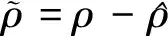
sΤ(t){[K*C(A+I)+NC]x(t)+

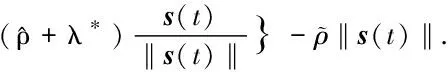
(55)

假設(shè)系統(tǒng)受到的未知噪聲干擾有界,即‖d‖≤d0．進(jìn)一步有:

(‖K*NFs‖+‖K*Fs‖)‖es(t)‖+

‖B+D‖d0]·‖s(t)‖≤

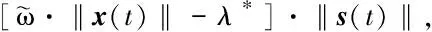
(56)

其中

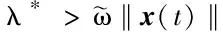
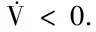
(57)

根據(jù)Lyapunov穩(wěn)定性理論可知,所設(shè)計的自適應(yīng)滑模容錯控制器能夠保證航天器姿控系統(tǒng)在陀螺儀故障情況下的漸近穩(wěn)定性．

4 仿真實例

令δ*=ε*=1,Q*=L1=I3,此時有λmax(Q*)=1,η*=1．選取圓形穩(wěn)定域D(0,1),學(xué)習(xí)速率τ=0.001,并選取如下參數(shù)矩陣:

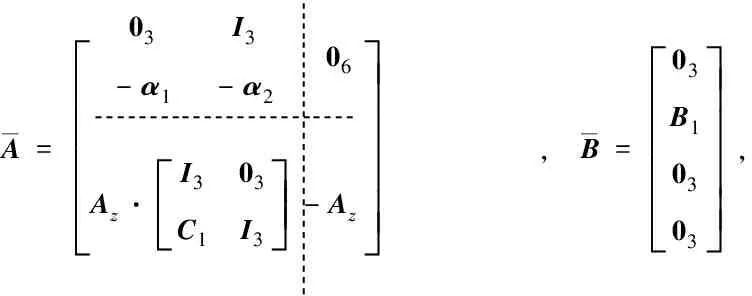
A=é?êêêê03I3-α1-α206Az·I303C1I3é?êêù?úú-Azù?úúúú, B=03B10303é?êêêêù?úúúú,

其中：

Az=diag{-1,-1,-1,-1,-1,-3},

w0=0.001 rad/s,

Ix=12.49 kg·m2,

Iy=13.85 kg·m2,

Iz=15.75 kg·m2,

利用LMI工具箱feasp求解器求解不等式(55)、(56)和(57),得到觀測器增益矩陣L和L2分別為

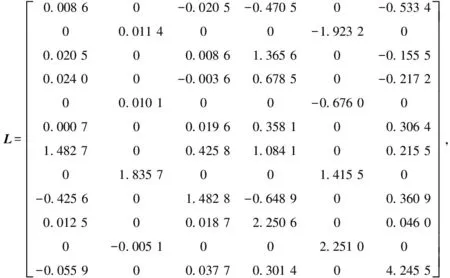
根據(jù)以上給出的仿真參數(shù)和增益矩陣,可以利用Simulink搭建航天器姿控系統(tǒng)增廣P型學(xué)習(xí)觀測器．三種常見故障類型的仿真結(jié)果如圖1—3所示．

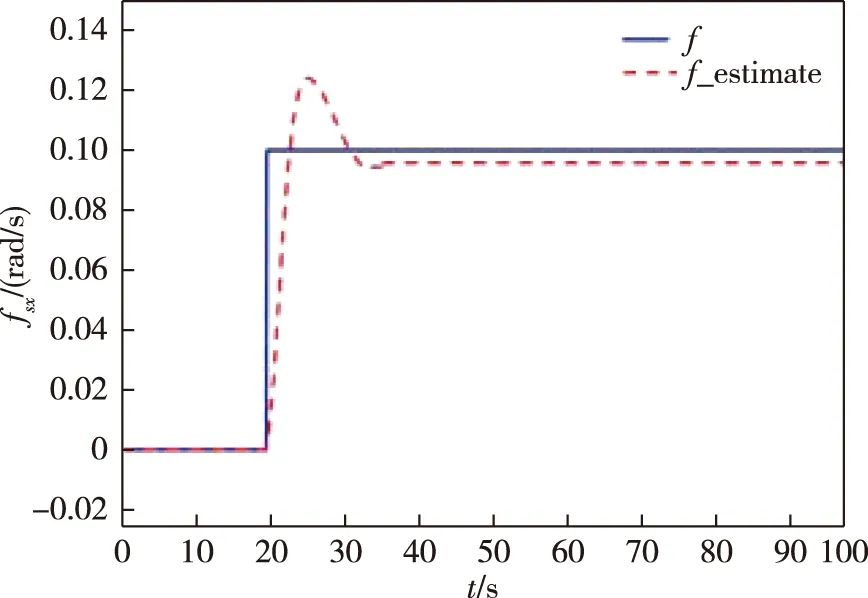
圖1 滾動軸陀螺加性突變故障重構(gòu)Fig.1 Fault reconstruction of rolling axis gyro with additive sudden change fault

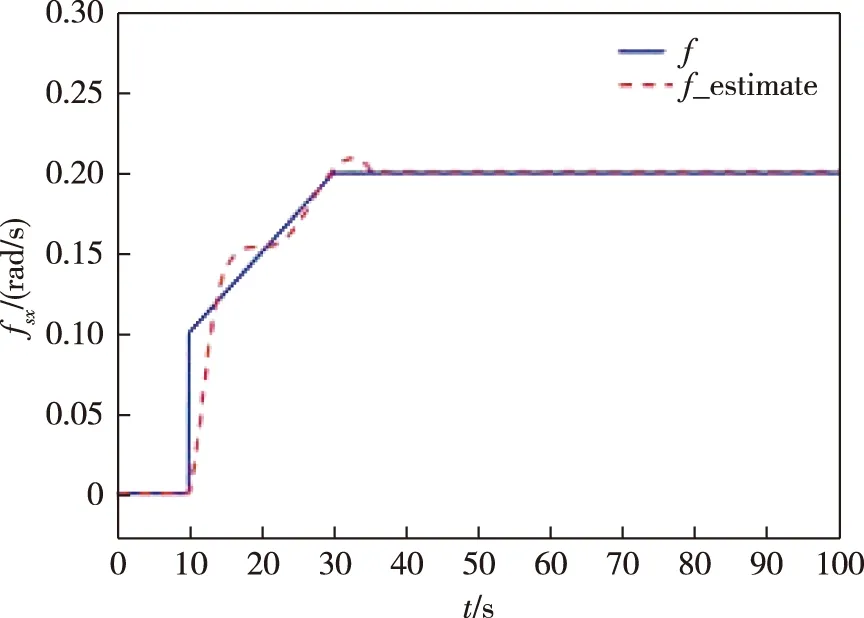
圖2 滾動軸陀螺加性時變故障重構(gòu)Fig.2 Fault reconstruction of rolling axis gyro with additive time-varying fault

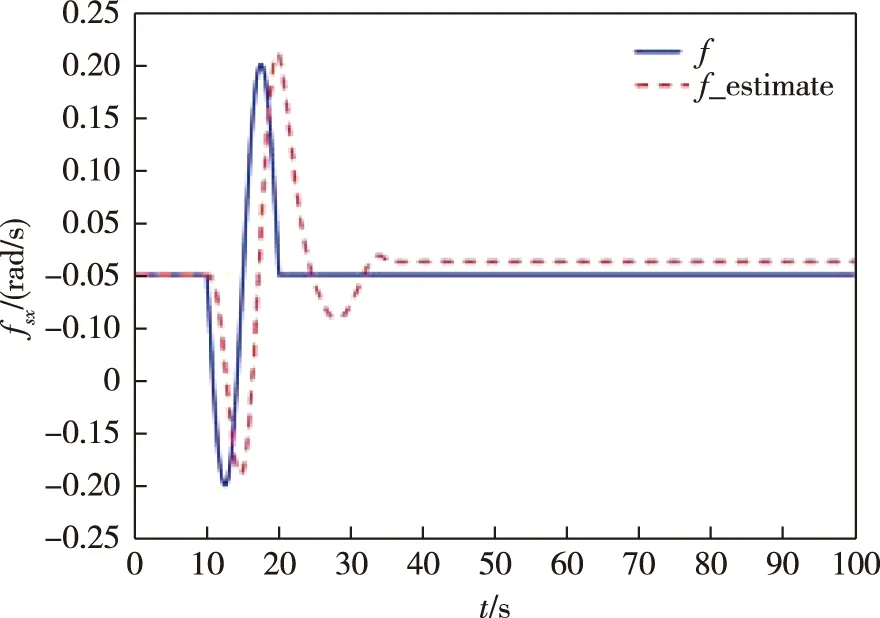
圖3 滾動軸陀螺加性正弦時變故障重構(gòu)Fig.3 Fault reconstruction of rolling axis gyro with additive sinusoidal time-varying fault

1)滾動軸陀螺儀發(fā)生加性突變故障:

2)滾動軸陀螺儀發(fā)生加性時變故障:

3)滾動軸陀螺儀發(fā)生加性正弦時變故障：

從圖1—3可以看出,采用增廣P型學(xué)習(xí)觀測器能夠?qū)σ陨先N類型的傳感器故障實現(xiàn)重構(gòu),驗證了算法的可行性．但可以看出,這種故障估計方法對故障的估計有時不夠精確．在故障突然發(fā)生時,對故障信號的響應(yīng)不夠及時;在故障消失或穩(wěn)定后,仍存在一定的估計誤差．可見該觀測器對緩變故障的重構(gòu)效果較好,對陡變故障的重構(gòu)效果較差．

接下來,利用定理2設(shè)計自適應(yīng)主動容錯控制器提高故障系統(tǒng)的穩(wěn)定性．

首先,利用Matlab/LMI工具箱feasp求解器求解不等式(50),得到矩陣P和N．然后選取參數(shù)λ*=υ*=1,同時假設(shè)在t0時刻yc(t0)=0．

假設(shè)滾動軸陀螺發(fā)生如下形式的加性正弦時變故障:

采用傳統(tǒng)PD控制器和采用本文所設(shè)計的容錯控制器的仿真結(jié)果如圖4—7所示．

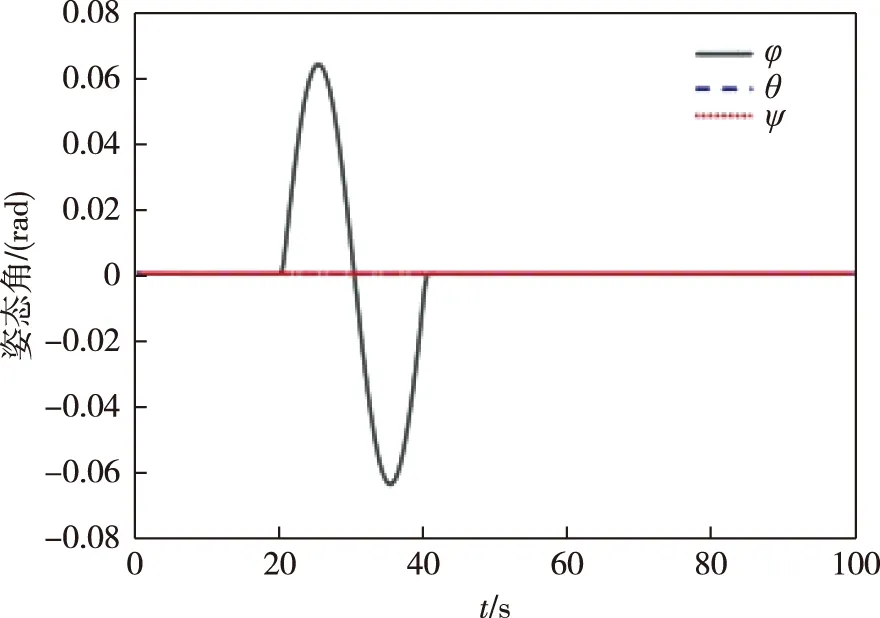
圖4 陀螺加性正弦時變故障情況下傳統(tǒng)PD控制器姿態(tài)角控制效果Fig.4 Attitude angle control effect of traditional PD controller under additive sinusoidal time-varying fault of gyro

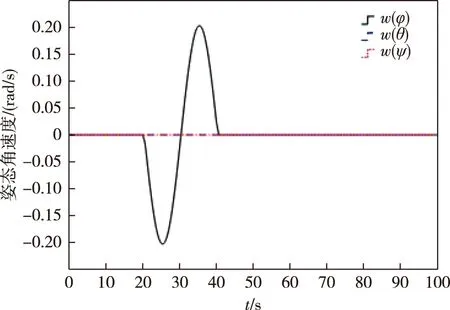
圖5 陀螺加性正弦時變故障情況下傳統(tǒng)PD控制器姿態(tài)角速度控制效果Fig.5 Attitude angular velocity control effect of traditional PD controller under additive sinusoidal time-varying fault of gyro

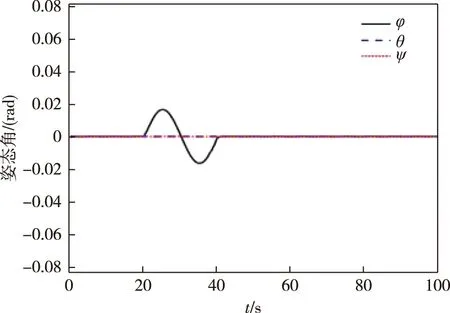
圖6 陀螺加性正弦時變故障情況下自適應(yīng)滑模容錯控制器姿態(tài)角控制效果Fig.6 Attitude angle control effect of adaptive sliding mode controller under additive sinusoidal time-varying fault of gyro

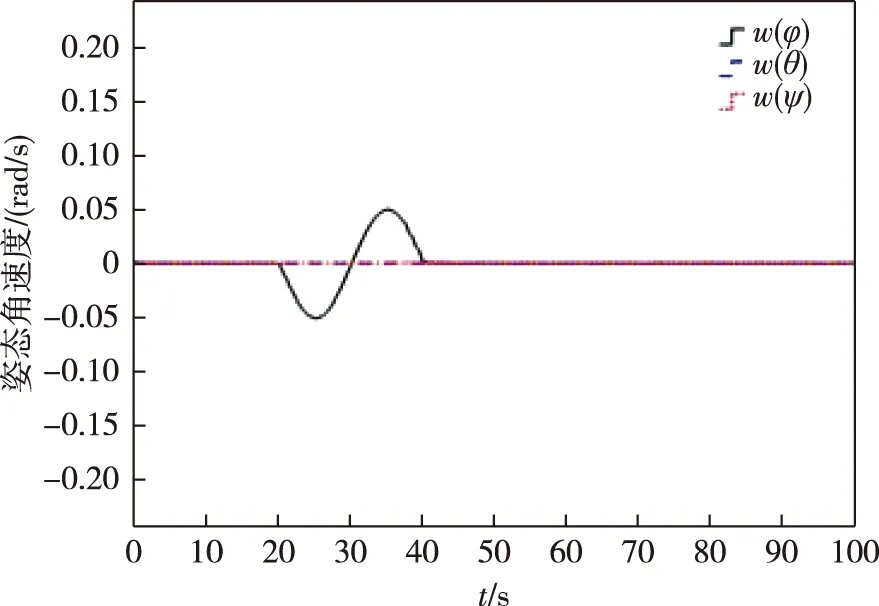
圖7 陀螺加性正弦時變故障情況下自適應(yīng)積分滑模容錯控制器姿態(tài)角速度控制效果Fig.7 Attitude angular velocity control effect of adaptive sliding mode controller under additive sinusoidal time-varying fault of gyro

對比觀察圖4—7可以看出,在采用自適應(yīng)積分滑模容錯控制器后,航天器滾動軸姿態(tài)角和姿態(tài)角速度在相同的故障時間內(nèi)變化幅度減小．其中姿態(tài)角變化范圍大致從±0.065 rad變化到了±0.015 rad,姿態(tài)角速度變化范圍大致從±0.19 rad/s變化到了±0.05 rad/s,系統(tǒng)的穩(wěn)定性有了明顯的改善．這可以說明積分滑模能夠提高系統(tǒng)的魯棒性,同時能夠驗證所設(shè)計自適應(yīng)滑模主動容錯控制器的有效性．

5 結(jié)論

本文提出了一種能夠在線估計航天器姿控系統(tǒng)傳感器故障的增廣P型學(xué)習(xí)觀測器.在將傳感器故障等效考慮成偽執(zhí)行器故障后,將故障值近似看作與前一時刻故障估計值和當(dāng)前時刻輸出估計誤差有關(guān)的兩項,實現(xiàn)了對未知傳感器故障的重構(gòu)．在此基礎(chǔ)上,基于自適應(yīng)技術(shù)和滑模理論,設(shè)計自適應(yīng)主動容錯控制器,并利用Lyapunov穩(wěn)定性理論對改進(jìn)后的模型進(jìn)行了穩(wěn)定性分析．仿真結(jié)果可以說明本文所設(shè)計的P型學(xué)習(xí)觀測器和自適應(yīng)容錯控制器均滿足系統(tǒng)設(shè)計要求．