面向估計性能的雙通道帶寬分配策略研究

彭志榮 趙矚華 陳惠珍 李偉雄 陳相德

0 引言

網絡化控制系統(NCSs)將網絡空間和物理空間聯系起來,使控制器、執行器、傳感器等系統組件之間的信號傳輸以網絡通信的方式實現，這能極大地簡化系統布線、優化產品構造,因此NCSs在工業控制等領域得到了廣泛應用[1-3]．在實際控制中,因帶寬受限,以及傳輸協議、網絡流量等因素的影響,系統組件間的信號傳輸存在時滯．由于時滯具有未知性、隨機性、時變性,使得系統的分析與設計變得復雜．為了解決時滯現象所帶來的問題,針對離散時間域,本文考慮將系統建模為具有多個模態并且各模態間存在一定轉移概率的隨機系統,即Markov跳變系統[4-5]．將Markov跳變系統應用于網絡化控制,已成為許多學者研究的課題．文獻[6]將網絡引起的隨機延遲建模為Markov鏈,然后將所得的閉環系統轉換為Markov跳變線性系統,在此模型的基礎上,提出了不確定NCSs魯棒有限時間隨機穩定的充分條件;文獻[7]用隱Markov模型描述了系統和控制器之間出現的異步現象,針對Markov跳變系統解決了異步無源控制問題；文獻[8]研究了具有通信限制和環境干擾的網絡化控制H∞輸出跟蹤控制問題,將隨機時間延遲和數據包丟失分別描述為兩個隨機Markov鏈．

網絡通信將眾多孤立的設備通過網絡聯系起來,信號在數據鏈路中傳輸,實現信息的互通．近十幾年來,網絡通信技術快速發展,從城市到鄉村幾乎都有網絡覆蓋,網絡通信已成為人們生產生活中至關重要的一部分．現有的網絡通信方式多種多樣,傳統互聯網通信包括Wi-Fi傳輸、以太網通信，移動空中網有GPRS無線通信、NB-IOT通信、4G通信等[9-10]．文獻[11]利用Wi-Fi設備中可訪問的細粒度通道狀態信息的相位和幅度的特點,設計室內跌倒檢測系統;文獻[12]分析了窄帶物聯網NB-IOT可以以三種模式進行部署,并介紹了NB-IOT的設計規范;文獻[13]分析了第五代移動通信技術的引入帶來的移動通信運行架構的轉變．盡管網絡通信技術已蓬勃發展,但是隨著人們對傳輸數據量需求的不斷增加，以及對傳輸速率的要求不斷提升,仍然需要改善和革新．

本文使用雙通道帶寬分配策略進行傳輸,可以將有限的帶寬靈活地分配于兩個通道,充分利用信道容量;每個通道在各自的諧振頻率處傳輸效率最高,因此可以對兩個通道做帶寬分配,根據實際負載大小、傳輸距離、數據量等因素選擇使用合適的通道進行傳輸．

本文結構如下:第1節描述了離散時間Markov時滯系統的系統模型、雙通道量化傳輸的方案以及估計器的設計;第2節建立了使時變估計誤差系統滿足H∞性能的充分條件,通過將遞歸矩陣不等式轉化為線性遞歸矩陣不等式,得出了估計器的增益矩陣設計的方法;第3節給出實例驗證了所設計的系統;第4節為總結．

注1本文中：Rn表示n維歐幾里得空間;Rn×m表示n行m列的實數矩陣集；上標“T”和“-1”分別表示矩陣的轉置和逆;P>0(P∈Rn×m)表示P是實對稱正定矩陣；I表示相應階數的單位矩陣；*表示對稱矩陣中相應對稱的元素；diag{…}表示對角矩陣；E(x(k))表示x(k)的期望．

1 問題描述及系統建模

1.1 系統模型

考慮如下的離散時間馬爾可夫時滯系統:

(1)

其中x(k)=[x1,x2,…,xn]T∈Rn是系統狀態向量,y(k)∈Rm是系統的測量輸出,z(k)∈Rp是系統待估計信號,ω(k)∈Rq是外部擾動輸入并且屬于空間L2∈[0,∞),f(·)是非線性函數并且滿足假設1,d(k)是未知的但滿足d1≤d(k)≤d2的正整數時滯,{θ(k),k∈Z+}是一個離散的馬爾可夫鏈,它的取值范圍是一個有限狀態集合S={1,2,…,N}．假定系統整個轉移概率矩陣都是已知的,并用Π=[πij]i,j∈S來表示,其中從k時刻所處模態i轉移到k+1時刻所處的模態j的概率用πij=Pr(θ(k+1))=j|θ(k)=i≥0,?i,j∈S,k∈Z+表示．矩陣Aθ(k),Bθ(k),Cθ(k),Dθ(k),Eθ(k)和Lθ(k)是已知的并具有合適維度的系數矩陣．

1.2 雙通道量化傳輸

由于帶寬是有限的,使用量化器可以在一定程度上克服帶寬約束,充分利用信道容量．在離散時間馬爾可夫時滯系統的狀態估計中,本文更重視小信號,所以采用非均勻的對數量化器,也就是信號幅值小的地方量化等級越多,能夠保證小信號的精度．對數量化器定義如下:

yq(k)=Q(y(k)),

(2)

其中Q(y(k))=[q1(y1(k))q2(y2(k)) …

(3)

其中δi=(1-ρi)/(1+ρi)．量化誤差ei(k)可以描述為

ei(k)?qi(yi(k))-yi(k)=Δi(k)yi(k),

(4)

其中Δi(k)∈[-δi,δi],則量化后的信號可以描述為

yq(k)=(I+Δ(k))y(k),

(5)

其中Δ(k)=diag{Δ1(k),Δ2(k),…,Δm(k)}．

傳輸數據的所需信道容量,與所使用量化器的量化密度有關．量化密度越大,傳輸的數據就越準確,但需要更多的信道容量．量化密度為ρi時,對數量化器量化后的數據所需容量Cdi如下:

(6)

由于yq(k)=[y1q(k)y2q(k) …ymq(k)]T∈Rm,采用雙通道傳輸,量化傳輸分為以下兩種情況:

情況1m為偶數,通道1傳輸m/2維的數據,量化密度ρi=ρ1,i∈ψa?{1,2,…,m/2};通道2傳輸m/2維的數據,量化密度ρi=ρ2,i∈ψb?{(m+2)/2,(m+4)/2,…,m}．

情況2m為奇數,通道1傳輸(m+1)/2維的數據,量化密度ρi=ρ1,i∈ψc?{1,2,…,(m+1)/2};通道2傳輸(m-1)/2維的數據,量化密度ρi=ρ2,i∈ψd?{(m+3)/2,(m+5)/2,…,m}．

由于帶寬有限,因此對數量化后總的數據容量應小于或等于限定值,記限定值為C,則

C1Cd1+C2Cd2≤C,

(7)

其中C1,C2分別為通道1、通道2的傳輸數據量,Cd1,Cd2分別是量化密度為ρ1,ρ2時對數量化器量化后的數據所需容量．

1.3 估計誤差系統

考慮如下形式的估計器:

(8)

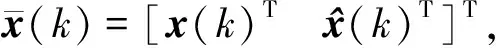
(9)

其中

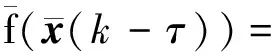
(10)

為了方便對系統做H∞性能分析,引入以下假設、引理和定義．

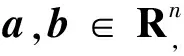
[fis(a)-fis(b)-F1is(a-b)]T×

[fis(a)-fis(b)-F2is(a-b)]T≤0，

(11)

其中F1is,F2is為已知實矩陣．

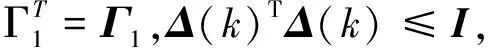
當且僅當存在標量ε>0,使下列不等式成立:

定義1[16]給定一個標量γ>0,如果零初始條件下,下列不等式對于所有非零v(k)均成立,則估計器誤差系統具有H∞噪聲衰減性能指數γ:

(12)

2 主要結論

2.1 H∞性能分析

本節對估計誤差系統(9)的H∞性能進行分析,并給出定理1．首先定義符號:

τ1=diag{τ11,τ11},

τ2=diag{τ12,τ12},

(13)

定理1給定一個標量γ>0,如果存在矩陣:

Pr>0,P1>0,r={1,2,…,N},

ε1=diag{ε11,ε12}∈R2n×2n(ε1≥0),

ε2=diag{ε21,ε22}∈R2n×2n(ε2≥0)

使得下列不等式成立,則估計誤差系統(9)滿足H∞性能．

(14)

證明引入以下二次函數來分析時變估計誤差系統(9)的H∞性能:

(15)

其中Pθ(k)>0,P1>0．

定義θ(k)?r,θ(k+1)?s,并且從均值的意義上定義二次函數(15)的差,如下所示:

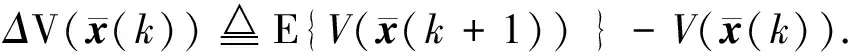
(16)

將誤差系統(9)代入式(16)可得:

(17)

其中:

考慮非線性情況下,根據假設1可得(18)、(19)兩個不等式：

(18)

(19)

根據上面得到的兩個非線性的不等式條件,不等式(17)滿足下面的不等式:

(20)

其中:

將(20)的兩邊從k=0到k=N求和,可以進一步得到:

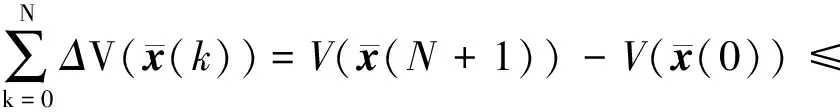
(21)

2.2 估計器設計

本節研究基于時變時滯馬爾可夫系統的估計器增益,使時變估計誤差系統(9)滿足H∞性能．

ε1=diag{ε11,ε12}(ε1≥0),

ε2=diag{ε21,ε22}(ε2≥0),

使得下列的不等式成立:

(22)

則時變估計誤差系統(9)滿足H∞性能．

其中:

Γ2=[εδCr(k) 0 0 0 0 0 0 0εδEr(k)0 0 0]，

Ξ22=-γ2I,

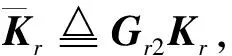
(23)

綜合考慮(10)和不等式

(24)

可以得到:

(25)

因此,條件(22)使得系統滿足:

根據定義1,估計誤差系統滿足H∞性能．證明完畢．

3 仿真實例

本節將通過一個仿真實例驗證所設計的面向估計性能的雙通道帶寬分配策略的有效性．假設系統中n=5,m=4,Markov模態數N=2,時滯參數d1=1,d2=2,量化器的量化密度范圍為ρi∈[0.5,0.95].若要傳輸4維數據,則根據式(6)可得量化后所需的總信道容量至少為1.908 4,至多為6.396 4．如果帶寬上限為4,如何根據雙通道量化傳輸方案分配帶寬,即如何調節兩個傳輸通道的量化密度使總信道容量被充分高效的利用、估計誤差較小并且系統對外部擾動有較好的抑制能力,成為被考慮的問題．

在本實例中,兩個通道的量化密度分別為0.726 4和0.881 3,量化后對應的所需容量分別為0.8和1.2,相應的系數矩陣如下所示:

時變非線性函數如下:

外部擾動為:ω(k)=0.8e-0.1k|sin(k)|,

馬爾可夫轉移概率矩陣如下:

根據第二節所述的定理并通過Matlab的LMI工具箱,可以得到H∞性能指標為γ=2.890 2,模態1和模態2的估計器增益分別如下:

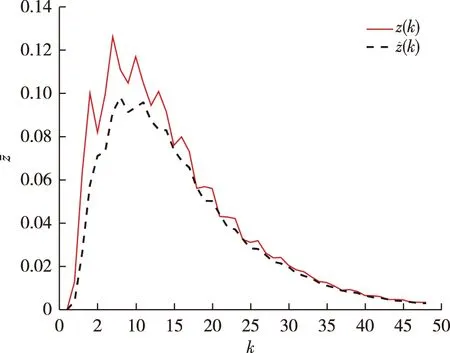
圖1 待估計信號z(k)和估計信號Fig.1 Signal to be estimated z(k) and estimated signal

注2本實例僅采用一組量化密度設計出該雙通道量化情況下能達到最佳性能的系統．在實際應用中,應根據所傳輸信號中各部分信號分量幅值的大小設計適合的量化密度,也就是給各個通道分配適合的帶寬,從而設計出最佳系統．

4 結論

本文提出了面向估計性能的雙通道帶寬分配策略．將系統建模為Markov跳變時滯系統,可減小網絡化控制系統中時滯現象對信號傳輸的影響．采用雙通道傳輸策略,提升數據到達率,減少數據包的丟失．雙通道量化傳輸方案可將有限的帶寬靈活地分配于兩個通道,充分利用信道容量,提升傳輸效率．本文設計了估計器的增益矩陣以及滿足H∞性能的時變估計誤差系統,并通過實例驗證了所設計系統的有效性．