應用多星的空間目標跟蹤定位算法

喬鵬 呂曉寧 趙軍鎖 夏玉立 李濟民 周瑤

(中國科學院軟件研究所 天基綜合信息系統重點實驗室，北京 100190)

早期的衛星任務，衛星數量較少，星載探測設備種類較為單一，常常采用單星對空間碎片等空間目標進行定位與跟蹤。單星定位算法僅具備被動測角信息時，只能通過激光測距的方式對空間目標進行定位，但激光測距機因測頻的限制，受空間距離及空間環境的影響，探測空間碎片等空間目標的定位與跟蹤誤差較大[1]。隨著探測領域的發展，與單星的空間目標探測能力相比，多星協同任務規劃可以合理分配任務資源，結合各類衛星的在軌探測狀態與約束，具有較強的適應性和較廣的觀測范圍，可完成復雜的觀測任務[2]。因此，基于衛星搭建多星光學探測體系，解算空間碎片等空間目標的空間位置，實現空間目標的定位與跟蹤具有重要的研究意義。

近年來，基于衛星解算空間碎片等空間目標方面，國內外已開展多項研究。文獻[3]中研究了天基觀測空間碎片等空間目標的光譜特性，從而獲得空間目標的材料成分信息，為后續研究提供信息基礎。文獻[4]中分析了空間碎片探測譜段的響應程度，采用多光譜光學載荷進行空間碎片的探測，為空間碎片定位提供數據基礎。文獻[5]中對天基觀測空間碎片等空間目標進行建模，分析系統誤差對探測精度的影響，并設計有效方法抑制觀測與模型結構誤差對探測精度的影響。文獻[6]中首先分析了空間碎片成像特性，構建二維高斯擬合模型，采用核函數的設計，監測空間碎片。但是，采用單星激光測距的方式，成像軌跡受到距離與空間環境的影響，進而影響定位精度。現有空間碎片探測技術在空間坐標系中目標定位與航跡管理方面，其目標定位精度問題依舊面臨巨大挑戰，同時光學探測體系還會出現空間目標的星間信息丟失、衛星與目標共面場景。因此，本文面向多星探測領域，提出一種多星空間目標跟蹤定位算法。該算法基于三角交會原理[7]，建立空間坐標轉換模型與多星定位模型，關聯空間目標像點，解算空間目標軌跡，跟蹤空間目標。當產生空間目標信息丟失等異常情況時，引入加速度參數建模目標軌跡，改進卡爾曼濾波算法預測空間目標軌跡位置。

1 空間目標跟蹤定位算法

1.1 天基探測系統空間目標觀測模型

首先，構建分布式天基探測系統總體架構，搭建天地基一體化、柔性可變的協同系統，將多星分為中央控制衛星、中間信息傳輸衛星和底層執行衛星，如圖1所示。天基探測系統包括3個層級的衛星和地面控制中心。①第1個層級為中央控制衛星，該類衛星具有較強的智能性，是協同觀測系統中的主導者，可完成協同任務規劃、智能決策等工作。②第2個層級為中間信息傳輸衛星，該類衛星只做數據中間通信，負責底層執行衛星與中央控制衛星的通信。③第3個層級為底層執行衛星，該類衛星可實現終端智能，包括空間目標發現、識別、跟蹤，以及小范圍任務規劃功能。④地面控制中心包括系統控制中心與指令跟蹤站，它與中央控制衛星承擔著系統的最高智能決策和任務分配功能，是系統的核心組成部分。

圖1 天基探測系統架構Fig.1 Architecture of a space-based exploration system

天基探測系統可合理分配衛星資源，排列不同的時間窗，制定多星觀測空間目標的任務規劃，構建多星觀測空間目標的交會模型，通過中央控制衛星控制底層執行衛星進行空間目標的觀測定位。通過對多星坐標及空間目標坐標的三角交會原理，可以實現空間目標的位置解算。同時，各衛星數據統一到同一坐標系下進行交會解算。天基探測系統對多空間目標跟蹤時，可獲得空間目標相對于當前衛星坐標下的方向數據，方向數據與衛星高精度位置姿態數據結合轉換到交會坐標系下。

天基探測系統采用異址雙星方式，中央控制衛星確定系統觀測任務在統一時序控制下，各星對空間目標進行同步觀測，通過多星交會解算空間目標軌跡。以雙星異面交會算法在相機自身坐標系下為例，如圖2所示。圖2中，設坐標系為O-XYZ,光學衛星1位置O1坐標為[X01Y01Z01],空間目標(位置T)相對于光學衛星1的方位角與俯仰角為A1,E1，并且構成一條空間射線O1T1；光學衛星2位置O2坐標為[X02Y02Z02],空間目標(位置T)相對于光學衛星2的方位角和俯仰角分別為A2,E2，并且構成另一條空間射線O2T2。因實際光學設備的觀測誤差，雙星與空間目標間的向量稱作異面直線[8]。天基探測系統下的底層執行衛星進行觀測空間目標任務，空間目標成像投影與坐標系轉換統一為J2000坐標系。空間目標(位置T)相對于光學衛星1和2的方位、俯仰角需要進行坐標轉換，轉換步驟如下。

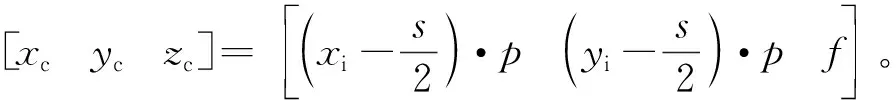
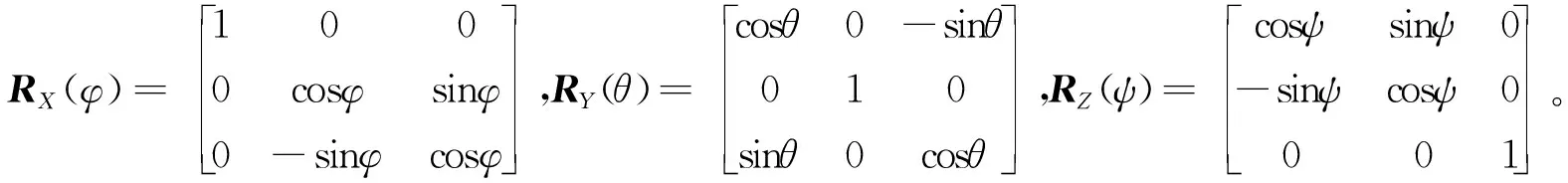
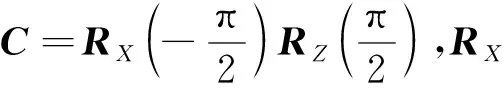
(4)地心軌道坐標系轉至J2000坐標系。將軌道面旋轉至與赤道面重合，需要進行3次坐標旋轉，通過軌道六根數可以得到軌道傾角γ、升交點赤經Ω和升交點角距u，則空間目標(位置T)在J2000坐標系下的坐標可表示為[xECIyECIzECI]T=H-1[xpypzp]T。其中：H=RZ(u)RX(γ)RY(Ω)。

利用J2000坐標系下的空間目標(位置T)相對于光學衛星1和2的坐標[xECI1yECI1zECI1]和[xECI2yECI2zECI2]，可由式(1)解算出空間目標(位置T)相對于光學衛星1和2的方位角A1、俯仰角E1與方位角A2、俯仰角E2。

(1)

設圖2中異面直線O1T1和O2T2的公垂線為l12,T1和T2分別為2條異面直線與其公垂線的交點，坐標分別為[X1Y1Z1]和[X2Y2Z2]。理論上，空間目標在異面直線O1T1和O2T2的公垂線上，確定衛星間空間目標像點關聯關系，可交會確定空間目標的坐標。

圖2 雙星交會算法原理Fig.2 Schematic diagram of double-satellite intersection algorithm

1.2 衛星間空間目標像點關聯

坐標系轉換后，天基探測系統的底層執行衛星之間需要計算不同像點之間的異面直線距離，關聯同一空間目標的星間像點。利用第1.1節像面坐標轉至J2000坐標下的步驟，假設像點i相對于光學衛星1的空間坐標為[X1iY1iZ1i],像點j相對于光學衛星2的空間坐標為[X2jY2jZ2j],光學衛星1的坐標為[x1y1z1]，光學衛星2的坐標為[x2y2z2]。具體求解的數學表達式為

(2)

式中：[dij]為2顆衛星間不同像點之間的異面直線距離矩陣。

計算出像點間的異面直線距離矩陣，當作最優化問題的匹配成本矩陣，這樣可通過最優化算法，最小化總匹配成本，找到同一空間目標在不同衛星所成像點的對應關系，以及同一空間目標在不同時刻所成像的對應關系。本文采用最近鄰點算法[9]將星間像點最優匹配問題建模為賦權二分圖求最優解的問題，原理為：若任意一個相等的子圖距離最近，可作為子圖的完美匹配，即匹配成本最小的一組匹配結果，得出已經完成匹配的空間目標標志號，以及匹配失敗的星間的空間目標標志號。

1.3 空間目標的跟蹤與定位

最優化求解出星間像點匹配關系，基于雙星交會模型解算空間目標軌跡及誤差計算公式[10]，分析影響定位精度的因素。

(3)

式中：m1，m2，K，l1，l2分別為光學衛星1和2交會模型的中間變量。

(4)

式中：加權系數ρ∈[0,1]；[xyz]為空間目標坐標。

這樣，求解出空間目標的坐標，便可對其進行跟蹤定位。

1.4 異常情況下的空間目標跟蹤

天基探測系統在軌觀測運行時，若空間目標觀測過程中出現星間信息丟失、空間目標與衛星共面情況，多星定位算法對空間目標的坐標預測誤差較大，跟蹤精度較低。

天基探測系統觀測空間目標出現異常情況時，通過中間信息傳輸衛星將異常行為指令反饋給中央控制衛星，中央控制衛星發出算法處理指令，底層執行衛星執行加入加速度分量的卡爾曼濾波算法[11]，預測空間目標在當前幀的軌跡位置，進而完成空間目標跟蹤任務。

傳統卡爾曼濾波算法[11]的目標軌跡建模如下。

(5)

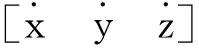
(6)

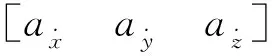
卡爾曼濾波算法首先采用時間更新方程來預估空間目標的坐標位置，時間更新方程為

X(k|k-1)=AX(k-1|k-1)+BU(k)

(7)

P(k|k-1)=AP(k-1|k-1)AT+Q

(8)

式中：X(k|k-1)為k時刻的過程狀態；X(k-1|k-1)為k-1時刻的最優狀態；A為狀態轉移矩陣；B為系統參數；U(k)為系統的調控量；P(k|k-1)與P(k-1|k-1)為k與k-1時刻狀態對應的協方差；Q為高斯白噪聲。

時間更新方程以當前狀態作為初始狀態，基于空間目標軌跡向量預測下一幀的空間目標狀態，即空間目標的坐標；預測完空間目標的位置，卡爾曼濾波算法采用狀態更新方程進行校正，狀態更新方程為

Kg(k)=P(k|k-1)HT/(HP(k|k-1)HT+R)

(9)

式中：Kg(k)為卡爾曼增益；H為觀測矩陣；R為測量噪聲對應的協方差矩陣。

X(k|k)=X(k|k-1)+Kg(k)(Z(k)-

HX(k|k-1))

(10)

式中：Z(k)為k時刻的觀測值；X(k|k)為k時刻的最優狀態。

P(k|k)=(I-Kg(k)H)P(k|k-1)

(11)

式中：I為單位矩陣；P(k|k)為X(k|k)狀態對應的協方差。

采用狀態更新方程將時間更新方程預測的軌跡位置與監測位置作差值，計算誤差協方差矩陣，迭代優化，得到空間目標的坐標值，進而跟蹤空間目標。

2 實例驗證

2.1 測試用例

通過STK軟件構建理論空間目標數據和觀測衛星的數據，模擬天基探測系統的衛星組網情況，構建4顆衛星組網觀測16個目標從太原飛往非洲的場景，具體的場景示意如圖3所示。其中：M1～M16為空間目標，飛行高度為550 km,飛行時長約為660 s。衛星對空間目標的可見時間段(日期2021-05-05,20幀每秒數據)分布如表1所示，其中持續時間為總幀數除以每秒幀數計算得出。

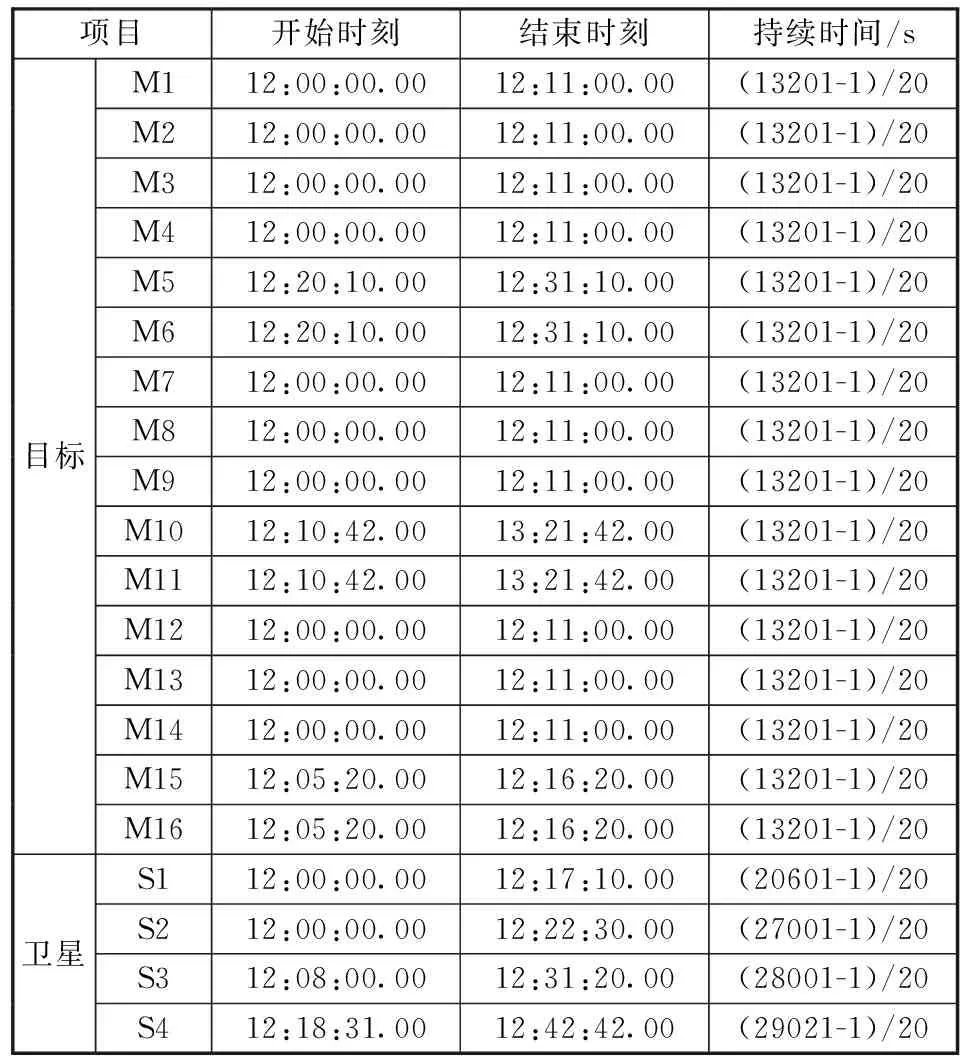
表1 衛星對空間目標的可見時間段Table 1 Observable time periods of satellites to space targets

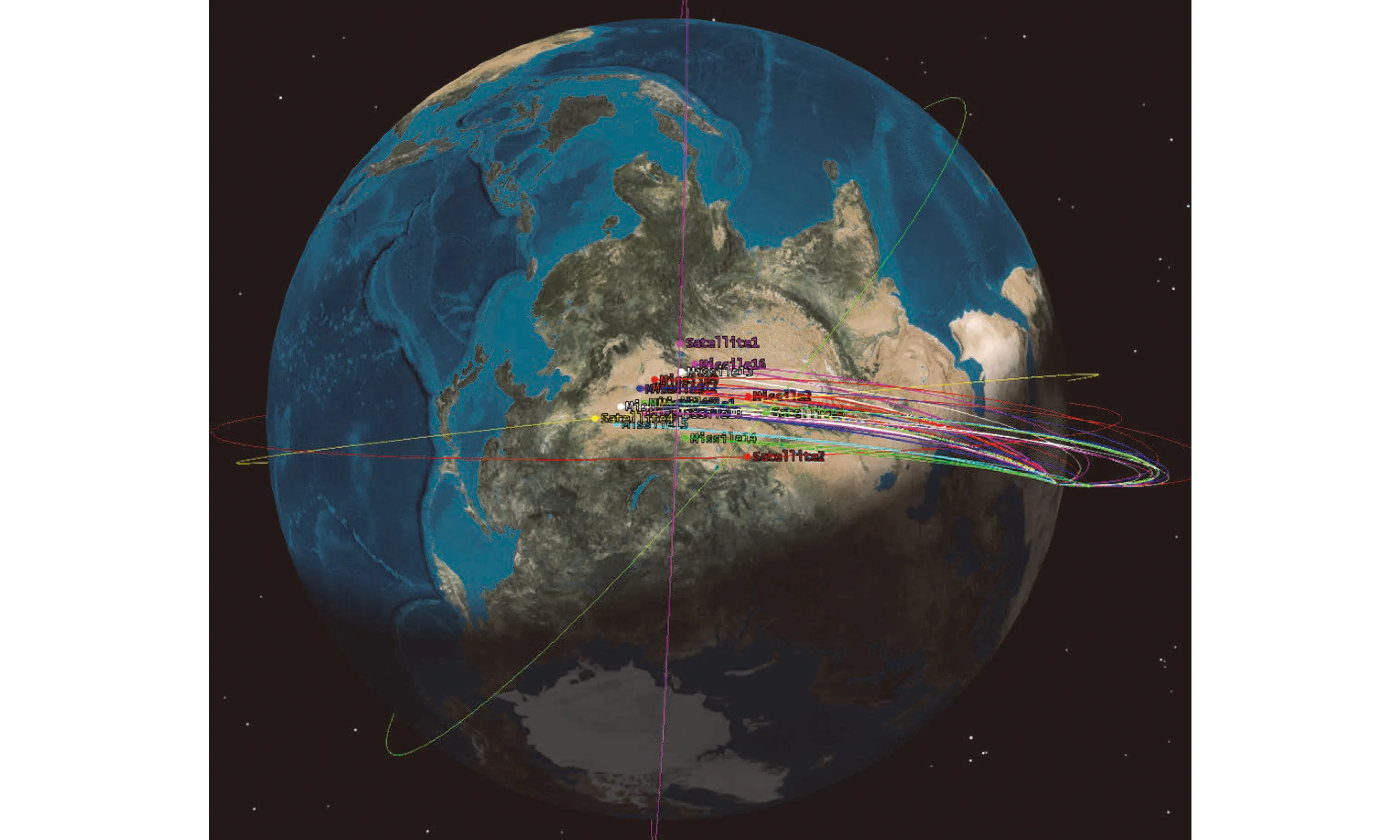
圖3 天基探測系統的衛星組網仿真Fig.3 Satellite networking simulation of space-based exploration system

取衛星編號S2與S3執行雙星觀測空間目標定位任務，測試用例見表2，共870 s的觀測數據，進行空間目標的跟蹤與定位。

表2 測試用例Table 2 Test case

實際衛星探測空間目標存在測量誤差，為模擬真實場景，本文附加的衛星站點位置誤差為15 m,衛星對空間目標的俯仰角與方位角誤差均為15″。

2.2 空間目標定位誤差分析

利用第2.1節的測試用例測試本文算法的可行性，測試空間目標定位算法的精度與跟蹤情況，如圖4所示。

由圖4可看出：X，Y，Z方向的位置誤差均在10 m以內，X方向的速度誤差在6 m/s以內，Y方向的速度誤差在8 m/s以內,Z方向的速度誤差在4 m/s以內。在前面15 s，X，Y，Z方向位置與速度誤差稍高一些，分析衛星間的空間目標關聯匹配需要一定的匹配時間，最近鄰算法匹配性能才能達到最優。持續一段時間后，算法趨于穩定狀況，位置誤差與速度誤差較低。

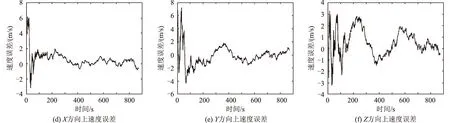
圖4 位置與速度誤差分析Fig.4 Position and velocity error analyses

下面統計本文算法對空間目標軌跡解算跟蹤的情況。成功跟蹤時，標志位置1；若未跟蹤，標志位置0。在870 s的觀測數據內，實時統計其空間目標跟蹤的準確率，具體如圖5所示。可以看出：采用本文算法，前15 s進行星間空間目標點的匹配關聯，15 s之后進行空間目標跟蹤處理，當天基探測系統底層執行衛星對空間目標的觀測數據一直存在時，采用本文的算法便能解算出空間目標軌跡，成功跟蹤空間目標。

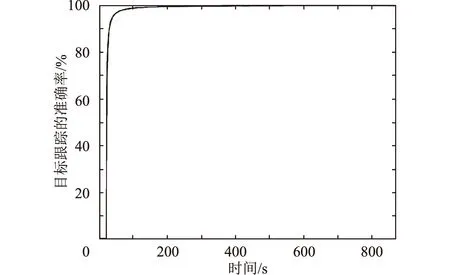
圖5 本文算法的空間目標軌跡解算情況Fig.5 Space target trajectory solution of algorithm in this paper

2.3 異常情況下空間目標跟蹤分析

當空間目標存在星間信息丟失、空間目標與衛星共面時，基于仿真輸入的測試用例，將編號S3衛星在12:12:00.00-12:12:20.00和12:16:00.00-12:16:20.00時間段內對空間目標的觀測數據作丟失處理，采用本文算法的跟蹤狀態見圖6。

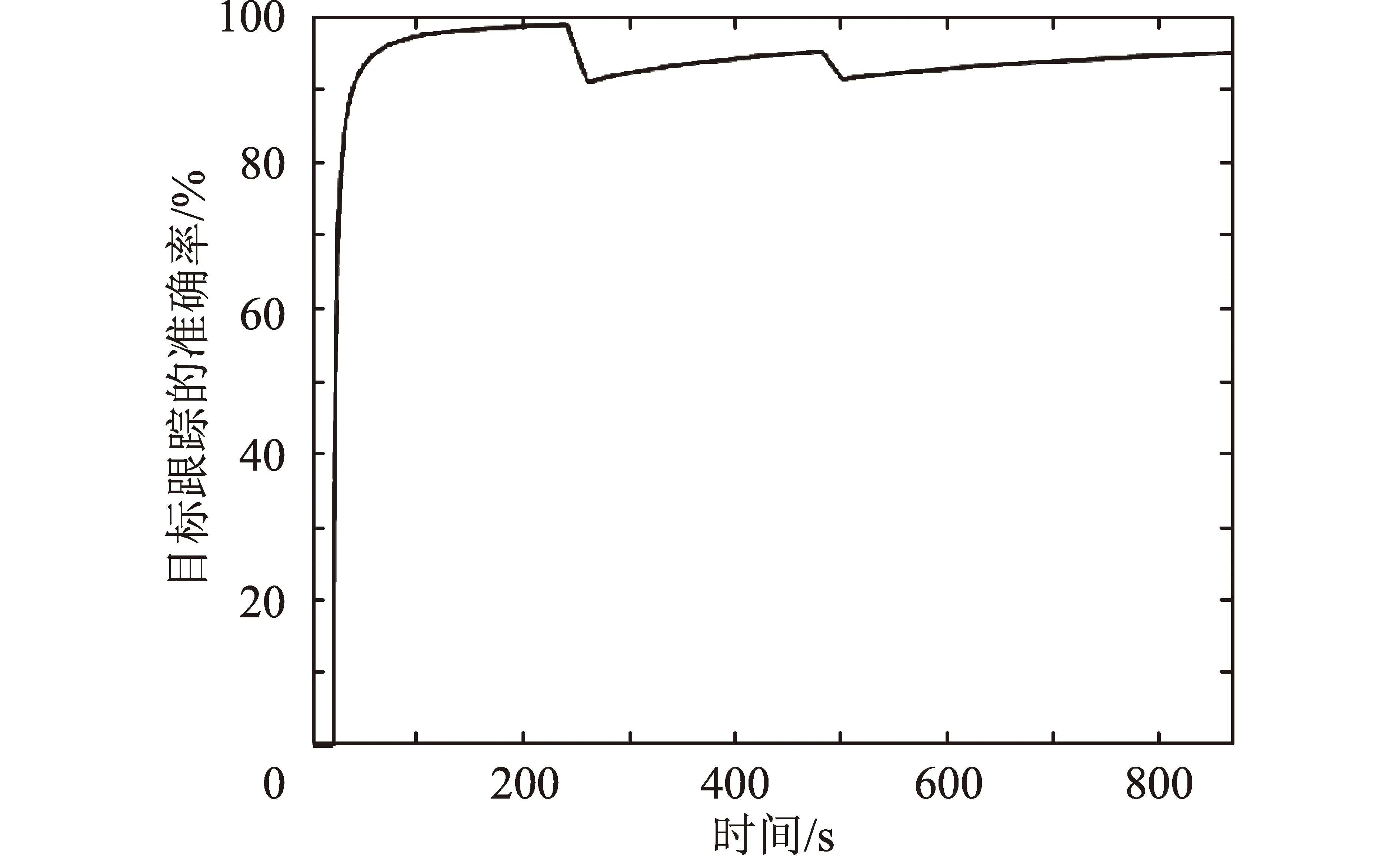
圖6 異常情況下空間目標跟蹤狀況Fig.6 Space target tracking status under abnormal conditions

底層執行衛星采用加入加速度分量的卡爾曼濾波算法預測空間目標在當前幀的軌跡位置，采用本文算法的跟蹤狀態見圖7。可以看出：輔以前面幾幀空間目標的位置、速度、加速度建模目標軌跡向量，結合卡爾曼濾波算法能有效提高空間目標的跟蹤精度。

圖7 異常情況下卡爾曼濾波算法空間目標跟蹤狀況Fig.7 Space target tracking status of Kalman filter algorithm under abnormal conditions

3 結束語

本文構建分布式天基探測系統總體架構，提出一種多目標跟蹤定位算法。該算法面向多星不同載荷平臺進行坐標轉換，計算觀測空間目標的異面直線距離，采用最近鄰算法最優匹配同一空間目標在不同衛星所成像點的對應關系，進而解算空間目標軌跡與空間目標跟蹤；當產生空間目標與衛星共面等異常情況時，本文構建目標軌跡向量引入加速度參數，采用卡爾曼濾波算法預測空間目標軌跡位置。通過STK軟件仿真數據進行實例驗證，結果表明：該算法的定位精度更高，當出現衛星間的空間目標信息丟失的場景時，結合卡爾曼濾波算法能有效提高空間目標的跟蹤精度。

本文算法可應用于天基觀測系統，完成在軌實時處理，工程可實施性強，可為分布式天基探測系統在軌監測空間碎片提供一種高效途徑；但該算法在雙星交會角處于180°周圍時存在測量條件劣化，導致探測空間目標軌跡時產生測量誤差，進而影響定位結果，下一步將重點研究該異常情況，構建合理的誤差傳遞模型，提高算法對異常情況的普適性。